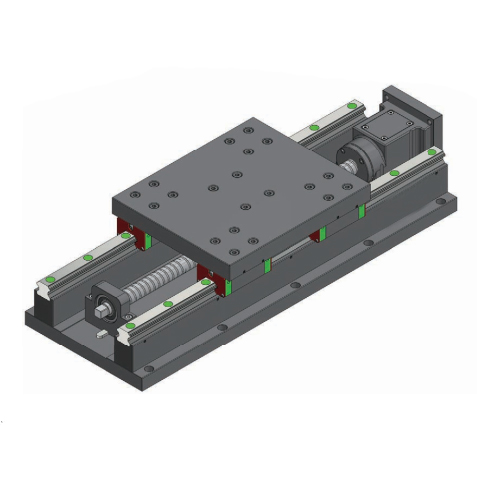
|
2-х координатный стол представляет собой основание с перемещающейся на нем крестовиной, на которой установлен рабочий стол. Для устранения зазора в крестовину вставлены регулируемые закаленные и шлифованные планки, а также стопоры хода. Основание установлено на ножки. Стол, крестовина и основание сделаны из высококачественной стали С-45А. Ходовые гайки сделаны из латуни с устройством компенсации зазоров в передаче винт-гайка. Маховики сделаны из алюминия и отполированы. Нижний ходовой винт защищен от попадания стружки специальными телескопическими пластинами, изготовленными из тонкой листовой стали. Предприятие-изготовитель сохраняет за собой право вносить изменения и дополнения в конструкцию изделия, не ухудшающие его технические характеристики. Вариант А
Ходовые винты крепятся к столу и основанию с помощью подшипников скольжения. Имеется один Т- образный паз 6Н9 и 6 резьбовых отверстий для закрепления заготовки. Вариант Б
Ходовые винты крепятся к столу и основанию с помощью 2-х пар радиально-упорных прецизионных подшипников. Вариант В
Ходовые винты крепятся к столу и основанию с помощью 2-х пар радиально-упорных прецизионных подшипников. Имеются три продольных и три поперечных взаимно перпендикулярных Т-образных паза 6Н9 для закрепления заготовки. По бокам стола имеются 6 резьбовых отверстий для установки заготовок. |
Имеется один Т-образный паз 6Н9 и 6 резьбовых отверстий для закрепления заготовки.
Показать все характеристики ↓ Стол двух координатный неповоротный АКР-2-20 предназначен для использования в качестве дополнительной оснастки преимущественно на универсальных фрезерных, шлифовальных, сверлильных станках.
Задать вопрос Фирма-производитель оставляет за собой право на внесение изменений в конструкцию, дизайн и комплектацию товара. |
02 мм
Пожалуйста, сверяйте информацию о товаре с информацией на официальном сайте компании производителя или уточняйте спецификацию конкретной модели с менеджером нашей компании.Автоматизированный координатный стол Л-5010-А
Автоматизированный координатный стол Л-5010-А предназначен для точного позиционирования деталей при лазерной сварке и наплавке. Стол обеспечивает перемещение обрабатываемых деталей по осям x и y , а также по вертикальной оси z (при использовании электромеханического подъемника стола). Управление столом может осуществляется при помощи автономного контроллера с джойстиком с возможностью программирования траектории движения или от компьютера.
В основе конструкции стола лежат шарико-винтовые пары (ШВП), линейные направляющие и шаговые двигатели.
Конструкция стола позволяет использовать различные типы ШВП, линейных направляющих и двигателей, что дает возможность варьировать точностные характеристики, длину хода и грузоподъемность координатного стола, адаптируя стол под конкретную задачу лазерной сварки и наплавки.
Координатный стол Л-5010-А предназначен для работы с установками для лазерной сварки и наплавки серий: ЛАТ, МУЛ, ЛАТ-С
Основные технические характеристики
| Размер рабочей поверхности | от 100х100 мм до 1000х1000 мм |
| Тип рабочей поверхности | с Т-образными пазами/плита с винтовыми креплениями |
| Тип и конструкция привода | ШВП, линейные направляющие, шаговые двигатели |
| Ход стола (по оси x и оси y) | от 100х100 мм до 1000х1000 мм |
| Точность позиционирования | ± 0,01-0,05 мм (в зависимости от типа ШВП и линейных направляющих, грузоподъемности) |
| Скорость перемещения | до 100 мм/сек |
| Грузоподъемность | до 60 кг |
| Ось z (вертикальный подъемник) | ход: до 500 мм, шаговый двигатель или двигатель постоянного тока, грузоподъемность: до 100 кг |
| Управление | автономный контроллер с джойстиком/компьютер |
Автономный контроллер управления с джойстиком ТМС-2
Автономный контроллер управления обеспечивает синхронную работу координатного стола и лазерной установки, а также позволяет задавать в ручном или программном режиме сложные траектории движения стола, которые могут состоять из линий, кругов и дуг.
Контроллер оборудован джойстиком, задающим направление движения стола, а также функциональными кнопками. Дисплей контроллера совмещен с дисплеем пульта управления лазерных установок серий ЛАТ, МУЛ, ЛАТ-С.
Основные возможности контроллера управления координатным столом:
- Два режима работы: ручной режим позиционирования (направление движения задается джойстиком, запуск лазера осуществляется педалью по усмотрению оператора) и программный режим (направление движения программируется путем “обкатки” необходимой траектории сварки или наплавки и расстановки точек начала/конца траектории (линия, круг, дуга), после нажатия кнопки “пуск” осуществляется сварка или наплавка по запрограммированной траектории с установленными параметрами работы лазера).
- Базовая модификация контроллера (ТМС-2(Б)) позволяет программировать простые траектории (одна линия или один круг).
- Расширенная модификация контроллера (ТМС-2(Р)) позволяет программировать сложные траектории, состоящие из нескольких линий, кругов или дуг, а также позволяет сохранять в памяти несколько вариантов таких траекторий.
- Расширенная модификация контроллера (ТМС-2(Р)) оснащена строчным дисплеем, на котором отображаются основные параметры работы контроллера (номер траектории, вид элемента траектории, системные сообщения и т.п.).
- Позволяет задавать скорость движения и величину перекрытия пятна лазерного излучения, а также управлять основными параметрами лазера.
- Позволяет управлять вертикальной z-осью стола.
Конструктивная гибкость и дополнительные возможности
Система управления координатного стола Л-5010-А легко адаптируется под конкретную задачу лазерной сварки и наплавки. Использование различных типов ШВП, линейных направляющих и двигателей, дает возможность варьировать точностные характеристики, длину хода и грузоподъемность стола.
Если вы не обнаружили в предлагаемом координатном столе и его контроллере необходимых вам параметров или функций, то мы можем доработать его по вашим требованиям.
Дополнительная информация о координатном столе
Видео обзор основных возможностей координатного стола и автономного контроллера (на примере установки серии ЛАТ-С):
youtube.com/embed/_9RBDuy73oo?rel=0″ frameborder=”0″/>
Стол 2-х координатный KRS-225 PROMA
Параметры | 100007 KRS-225 |
Длина рабочей поверхности A, (мм) | 225 |
Ширина рабочей поверхности B, (мм) | 175 |
Ширина паза рабочей поверхности C, (мм) | 12 |
Количество пазов | 2 |
Расстояние между пазами рабочей поверхности D, (мм) | 72 |
Общая высота G, (мм) | 110 |
Длина базовой платформы J, (мм) | 230 |
Ширина базовой платформы Н, (мм) | 180 |
Расстояние между крепежными отверстиями базы К, (мм) | 160/150 |
Количество крепежных мест | 4 |
Габарит маховика E, (мм) | 95 |
Продольная подача X, (мм) | 126 |
Поперечная подача Y, (мм) | 120 |
Цена деления шкалы маховика, (мм) | 0. |
Масса, (кг) | 16 |
01Характеристики и комплектация могут быть изменены фирмой-производителем без предварительного уведомления. Доставка: Компания “ТЕХНО Электрикал” осуществляет продажу и доставку Стол 2-х координатный KRS-225 PROMA по Москве и в любой регион России. Стоимость доставки рассчитывается отдельно. Уточнить условия покупки можно у менеджера по телефону +7 (495) 308-79-79.
Графические квадратные уравнения с использованием оси симметрии
Квадратное уравнение это многочлен уравнение степень 2 . Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + c
куда
а
,
б
а также
c
все реальные числа и
а
≠
0
.
Если мы заменим 0 с участием у , то получаем квадратичная функция
у знак равно а Икс 2 + б Икс + c
чей график будет парабола .
Осью симметрии этой параболы будет линия Икс знак равно – б 2 а . Ось симметрии проходит через вершину, поэтому Икс -координата вершины – б 2 а .Заменять Икс знак равно – б 2 а в уравнении, чтобы найти у -координата вершины. Заменить еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения и нанесите точки. Присоединяйтесь к ним и вытяните параболу.
Пример 1:
Постройте параболу
у
знак равно
Икс
2
–
7
Икс
+
2
.
Сравните уравнение с у знак равно а Икс 2 + б Икс + c найти значения а , б , а также c .
Здесь, а знак равно 1 , б знак равно – 7 а также c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение ось симметрии .
График квадратного уравнения в виде
у
знак равно
а
Икс
2
+
б
Икс
+
c
осью симметрии является линия
Икс
знак равно
–
б
2
а
. Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
–
(
–
7
)
2
(
1
)
или
Икс
знак равно
7
2
.
Заменять Икс знак равно 7 2 в уравнении, чтобы найти у -координата вершины.
у знак равно ( 7 2 ) 2 – 7 ( 7 2 ) + 2 знак равно 49 4 – 49 2 + 2 знак равно 49 – 98 + 8 4 знак равно – 41 год 4
Следовательно, координаты вершины равны
(
7
2
,
–
41 год
4
)
.
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно Икс 2 – 7 Икс + 2 |
| 0 | 2 |
| 1 | – 4 |
| 2 | – 8 |
| 3 | – 10 |
| 5 | – 8 |
| 7 | 2 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 2:
Постройте параболу у знак равно – 2 Икс 2 + 5 Икс – 1 .
Сравните уравнение с у знак равно а Икс 2 + б Икс + c найти значения а , б , а также c .
Здесь, а знак равно – 2 , б знак равно 5 а также c знак равно – 1 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде
у
знак равно
а
Икс
2
+
б
Икс
+
c
осью симметрии является линия
Икс
знак равно
–
б
2
а
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
–
(
5
)
2
(
–
2
)
или
Икс
знак равно
5
4
.
Заменять Икс знак равно 5 4 в уравнении, чтобы найти у -координата вершины.
у знак равно – 2 ( 5 4 ) 2 + 5 ( 5 4 ) – 1 знак равно – 50 16 + 25 4 – 1 знак равно – 50 + 100 – 16 16 знак равно 34 16 знак равно 17 8
Следовательно, координаты вершины равны
(
5
4
,
17
8
)
.
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно – 2 Икс 2 + 5 Икс – 1 |
| – 1 | – 8 |
| 0 | – 1 |
| 1 | 2 |
| 2 | 1 |
| 3 | – 4 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 3:
Постройте параболу Икс знак равно у 2 + 4 у + 2 .
Здесь, Икс является функцией у . Парабола открывается «вбок», а ось симметрии параболы горизонтальна. Стандартная форма уравнения горизонтальной параболы: Икс знак равно а у 2 + б у + c куда а , б , а также c все реальные числа и а ≠ 0 а уравнение оси симметрии имеет вид у знак равно – б 2 а .
Сравните уравнение с
Икс
знак равно
а
у
2
+
б
у
+
c
найти значения
а
,
б
, а также
c
.
Здесь, а знак равно 1 , б знак равно 4 а также c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде Икс знак равно а у 2 + б у + c осью симметрии является линия у знак равно – б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид у знак равно – 4 2 ( 1 ) или у знак равно – 2 .
Заменять
у
знак равно
–
2
в уравнении, чтобы найти
Икс
-координата вершины.
Икс знак равно ( – 2 ) 2 + 4 ( – 2 ) + 2 знак равно 4 – 8 + 2 знак равно – 2
Следовательно, координаты вершины равны ( – 2 , – 2 ) .
А теперь замените еще несколько у -значения в уравнении, чтобы получить соответствующие Икс -ценности.
| у | Икс знак равно у 2 + 4 у + 2 |
| – 5 | 7 |
| – 4 | 2 |
| – 3 | – 1 |
| – 1 | – 1 |
| 0 | 2 |
| 1 | 7 |
Постройте точки и соедините их, чтобы получить параболу.
квадратичных функций
квадратичных функцийСодержание : Эта страница соответствует § 3.1 (стр. 244) текста.
Предлагаемые задачи из текста:
с. 251 # 1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Стандартная форма
Приложения
Графики
Квадратичная функция имеет вид f (x) = ax 2 + bx + c , где a , b и c – числа, где a не равны нулю.
График квадратичной функции – это кривая, называемая параболой . Параболы могут открываться вверх или вниз
и различаются по «ширине» или «крутизне», но все они имеют одинаковую базовую U-образную форму. В
На рисунке ниже показаны три графика, и все они являются параболами.
Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекает его ось симметрии находится в точке, называемой вершиной параболы.
Вы знаете, что две точки определяют линию. Это означает, что если вам даны любые две точки на плоскости, то есть одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать относительно точек и квадратичных функции.
Учитывая три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой, существует ровно одна квадратичная функция f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт.График содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте поле под графиком. Если вы перетащите любую из точек, функция и парабола обновятся.
Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения / сжатия и сдвига.
2-5.Начнем с графика y = x 2 , сдвинем на 4 единицы вправо, затем
5 единиц вниз.
Упражнение 1 :
(a) Нарисуйте график y = (x + 2) 2 – 3. Ответ
(b) Нарисуйте график y = – (x – 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме .Когда квадратичная функция имеет стандартную форму, ее график легко построить, отражая, сдвигая и растяжение / сжатие параболы y = x 2 .
Квадратичная функция f (x) = a (x – h) 2 + k, не равная нулю, называется стандартной формой . Если а положительно, график открывается вверх, а если отрицательно, то открывается вниз. Линия симметрии – это вертикальная линия x = h, а вершина – это точка (h, k).
Любую квадратичную функцию можно переписать в стандартном виде, завершив квадратом . (См. Раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для завершения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не в решении уравнения.
Обратите внимание, что когда квадратичная функция имеет стандартную форму, ее нули также легко найти с помощью квадратного корня. принцип.
Пример 3 .
Запишите функцию f (x) = x 2 – 6x + 7 в стандартной форме. Нарисуйте график функции f и найдите его нули и вершина.
f (x) = x 2 – 6x + 7.
= (x 2 – 6x) + 7. Сгруппируйте члены x 2 и x и затем заполните квадрат на этих условиях.
= (x 2 – 6x + 9 – 9) + 7.
Нам нужно добавить 9, потому что это квадрат половины коэффициента при x, (-6/2) 2 = 9.
= (x 2 – 6x + 9) – 9 + 7. Мы видим, что x 2 – 6x + 9 – это полный квадрат, а именно (x – 3) 2 .
f (x) = (x – 3) 2 – 2.Это стандартная форма .
Из этого результата легко найти, что вершина графа f равна (3, -2).
Чтобы найти нули f, мы устанавливаем f равным 0 и решаем относительно x.
(x – 3) 2 – 2 = 0.
(x – 3) 2 = 2.
(x – 3) = ± sqrt (2).
х = 3 ± sqrt (2).
Чтобы нарисовать график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Когда мы
решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9
так что мы не меняем функцию. Если коэффициент при x 2 не равен 1, то мы должны вынести этот коэффициент из x 2 и
x, прежде чем продолжить.
Пример 4 .
Запишите f (x) = -2x 2 + 2x + 3 в стандартной форме и найдите вершину графика f.
f (x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.
= -2 (х 2 – х) + 3.
= -2 (x 2 – x + 1/4 – 1/4) + 3.
Мы складываем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 – коэффициент при x.
= -2 (x 2 – x + 1/4) -2 (-1/4) + 3.
Обратите внимание, что все в круглых скобках умножается на -2, поэтому, когда мы убираем -1/4 из круглых скобок, мы необходимо умножить на -2.
= -2 (x – 1/2) 2 + 1/2 + 3.
= -2 (х – 1/2) 2 + 7/2.
Вершина – это точка (1/2, 7/2). Поскольку граф открывается вниз (-2 <0), вершина является высшей точкой на графике.
Упражнение 2 :
Запишите f (x) = 3x 2 + 12x + 8 в стандартной форме.
Нарисуйте график функции f, найдите его вершину и найдите
нули f. ОтветАльтернативный метод поиска вершины
В некоторых случаях завершение квадрата – не самый простой способ найти вершину параболы. Если график квадратичная функция имеет два пересечения по оси x, тогда линия симметрии – это вертикальная линия, проходящая через среднюю точку х-перехватчиков.
Х-точки пересечения графика выше находятся в точках -5 и 3.Линия симметрии проходит через -1, что является средним -5 и 3. (-5 + 3) / 2 = -2/2 = -1. Как только мы узнаем, что линия симметрии x = -1, мы узнаем первую координату вершины -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.
Пример 5 .
Найдите вершину графика функции f (x) = (x + 9) (x – 5).
Поскольку формула для f разложена на множители, легко найти нули: -9 и 5.
Среднее значение нулей (-9 + 5) / 2 = -4/2 = -2. Итак, линия симметрии x = -2, а первая координата вершины -2.
Вторая координата вершины: f (-2) = (-2 + 9) (- 2-5) = 7 * (- 7) = -49.
Следовательно, вершина графика f равна (-2, -49).
Вернуться к содержанию
Приложения
Пример 6 .
У владельца ранчо есть 600 метров забора, чтобы ограждать прямоугольный загон с другим забором, разделяющим его посередине. как на схеме ниже.
Как показано на схеме, каждая из четырех горизонтальных секций забора будет иметь длину х метров, а три каждая вертикальная секция будет иметь длину y метров.
Цель владельца ранчо – использовать весь забор, а оградить как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому мы имеем
Общая площадь: A = 2xy.
Мы мало что можем сделать с величиной A, если она выражается как произведение двух переменных. Тем не мение, Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.
3г + 4х = 1200.
3y = 1200 – 4x.
y = 400 – 4x / 3.
Теперь у нас есть y, выраженный как функция от x, и мы можем подставить это выражение для y в формулу для общего площадь А.
A = 2xy = 2x (400 -4x / 3).
Нам нужно найти значение x, которое делает A как можно большим. A – квадратичная функция от x, а график открывается вниз, поэтому наивысшая точка на графике A – вершина. Поскольку A разложено на множители, самый простой способ найти вершина – найти пересечения по оси x и усреднить.
2x (400 -4x / 3) = 0.
2x = 0 или 400 -4x / 3 = 0.
x = 0 или 400 = 4x / 3.
x = 0 или 1200 = 4x.
х = 0 или 300 = х.
Следовательно, линия симметрии графика A равна x = 150, среднему от 0 до 300.
Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. уравнению, связывающему x и y.
y = 400 – 4x / 3 = 400-4 (150) / 3 = 200.
Вернуться к содержанию
Графические функции абсолютных значений | Purplemath
Purplemath
Принятие абсолютного значения отрицательного числа делает его положительным.По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу Т-диаграмму при построении графиков функций абсолютных значений. Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график.
Например, предположим, что ваш класс проходит следующую викторину:
MathHelp.com
Один из других учеников делает то, что обычно делает: он выбирает только положительные значения x для своей Т-диаграммы:
Затем он набирает свои очки:
Эти точки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график.В частности, они не содержат никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений что-то означают . В результате ученик забывает учесть эти столбцы и рисует ошибочный график:
НЕПРАВИЛЬНЫЙ ОТВЕТ!
Аааааи … он просто завалил викторину.
Но вы более осторожны.Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Итак, вы выбираете значения x , которые ставят «минус» внутри абсолютного значения, и выбираете еще несколько точек. Ваш T-график выглядит примерно так:
Затем вы наносите свои очки:
… и, наконец, вы соединяете точки:
У вас есть правильный график:
Правильный ответ!
Ааааанд… вы только что успешно прошли викторину. Хорошая работа!
Хотя графики абсолютных значений имеют тенденцию выглядеть так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает в себя абсолютное значение. Во всех случаях вам следует позаботиться о том, чтобы выбрать хороший диапазон значений x , потому что три соседних значения x почти наверняка не дадут вам достаточно информации, чтобы нарисовать достоверное изображение.
Примечание. Полоски абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (то есть положительные или нулевые). В результате буква «V» на приведенном выше графике появилась там, где знак внутри был равен нулю. Когда x было меньше –2, выражение x + 2 было меньше нуля, и столбцы абсолютных значений перевернули эти «минусовые» значения из-под оси x вверх. Когда x равняется –2, аргумент (то есть выражение внутри столбцов) равен нулю.Для всех значений x справа от –2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не меняли.
Другими словами, графически столбцы абсолютных значений заняли этот график:
… и перевернул «минус» (зеленый на графике) снизу оси x на верхнюю. Замечание, где аргумент столбцов абсолютного значения будет равен нулю, может быть полезным для проверки правильности построения графика.
Эта функция почти такая же, как и предыдущая.
Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, когда x = 0, поэтому я должен ожидать увидеть локоть в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютных значений, я ожидаю, что мой график будет выглядеть как обычный график абсолютных значений (представляющий собой букву «V» с изгибом в начале координат), но смещенный вверх на две единицы. .
Сначала я заполню свою Т-диаграмму, выбирая по ходу некоторые отрицательные значения x :
Затем нарисую точки и заполню график:
Партнер
Поскольку столбцы абсолютных значений всегда показывают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x .Но могут:
График
y = – | x + 2 |
Эта функция является своего рода противоположностью первой функции (выше), потому что в выражении абсолютного значения в правой части уравнения стоит «минус». Из-за этого «минуса» все положительные значения, предоставленные столбцами абсолютных значений, будут переключены на отрицательные значения.Другими словами, я должен ожидать, что этот график будет иметь изгиб в точке (–2, 0), как и первый график выше, но остальная часть графика будет перевернута вверх дном, чтобы оказаться ниже оси x .
Сначала я заполню свою Т-диаграмму:
Потом делаю свой график:
Также не предполагайте, что какой-либо график абсолютных значений всегда будет находиться только на одной стороне оси x .Графики могут пересекаться:
График
y = – | x | + 2
Моя Т-диаграмма:
… и мой график:
URL: https: // www.purplemath.com/modules/graphabs.htm
декартовых координат
Декартовы координаты могут использоваться, чтобы точно определить, где мы находимся на карте или графике.
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике с помощью , насколько далеко вдоль и , насколько далеко вверху :
| Точка (12,5) проходит на 12 единиц вдоль и на 5 единиц вверх. |
Их также называют Прямоугольные координаты , потому что мы как будто формируем прямоугольник.
Ось X и Y
| Направление влево-вправо ( по горизонтали ) обычно называется X . | |
| Направление вверх-вниз ( вертикальное ) обычно называется Y . |
| Сложите их вместе на графике … | |
… и мы готовы к работе | |
Там, где они пересекаются, это точка «0»,
| |
Ось : опорная линия, от которой расстояние измеряются.
Множественное число Axis – Axes , произносится как ax-eez
.Пример:
точка (6,4) это
6 единиц в поперечнике (в направлении x ) и
На 4 единицы вверх (в направлении y )
Так (6,4) означает:
Идите по 6, затем вверх по 4, затем «начертите точку».
И вы можете запомнить какая ось какая по:
x – это КРЕСТ, поэтому x находится ПОПЕРЕЧНО на странице.
Сложить вместе 2 числовые строки
Это похоже на то, как если бы мы соединили две числовые линии, одна идет влево-вправо, а другая – вниз-вверх.
Направление
При увеличении x точка перемещается дальше на вправо . | |
По мере увеличения y точка перемещается дальше на вверх на . |
Запись координат
Координаты всегда пишутся в определенном порядке:
- сначала горизонтальное расстояние,
- , затем вертикальное расстояние.
Это называется «заказанной парой » ( пара номеров в специальном заказе )
И обычно числа разделяются запятой, а вокруг всего этого ставятся круглые скобки:
(3,2)
Пример: (3,2) означает 3 единицы вправо и 2 единицы вверх
Пример: (0,5) означает 0 единиц вправо и 5 единиц вверх.
Другими словами, только на 5 единиц больше.
Происхождение
Точке (0,0) присваивается специальное имя «Начало», а иногда и буква «О».
Абсцисса и Ордината
Вы можете услышать слова «абсцисса» и «ордината» … это просто значения x и y:
- Абсцисса: значение по горизонтали (“x”) в паре координат: как далеко вдоль точка
- Ордината: значение по вертикали (“y”) в паре координат: насколько вверх или вниз точка
«Декартово»…?
Их называют декартовыми , потому что идея была развита математиком и философом Рене Декартом , который также был известен как Картезиус .
Он также известен тем, что сказал «Я думаю, следовательно, я» .
А как насчет отрицательных значений X и Y?
Как и в случае с числовой линией, у нас могут быть и отрицательные значения.
Отрицательный: начало с нуля и направление в противоположном направлении :
- Отрицательный x идет влево
- Отрицательный y идет вниз
Итак, для отрицательного числа:
|
Четыре квадрантаКогда мы включаем отрицательные значения, оси x и y делят пространство на 4 части: Квадранты I, II, III и IV (пронумерованы против часовой стрелки) |
В квадранте I и x, и y положительны, но…
- в квадранте II x отрицательно (y все еще положительно),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительно, а y отрицательно.
Как это:
|
Пример: точка «А» (3,2) находится на 3 единицы вперед и на 2 единицы вверх.
И x, и y положительны, поэтому эта точка находится в «квадранте I»
Пример: точка «C» (-2, -1) проходит на 2 единицы в отрицательном направлении и на 1 единицу вниз (т. Е. В отрицательном направлении).
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Примечание: слово Quadrant происходит от quad , что означает четыре . Например, четыре ребенка, рожденные при одном рождении, называются четвероногими , четвероногие животные – четвероногих .и четырехугольник представляет собой четырехсторонний многоугольник.
Размеры: 1, 2, 3 и более …
Подумайте об этом:
| 1 | Номерная линия может идти только: , поэтому для любой позиции нужно всего один номер |
|---|---|
| 2 | Декартовы координаты могут идти: , поэтому для любой позиции нужно два числа |
| 3 | Как определить точку в реальном мире (например, кончик носа)? Нам нужно знать:
, то есть три числа , или 3 измерения! |
3 Размеры
Декартовы координаты могут использоваться для определения местоположения точек в 3-х измерениях, как в этом примере:
| Здесь точка (2, 4, 5) показана в трехмерных декартовых координатах . |
На самом деле, эту идею можно продолжить в четырех и более измерениях – я просто не могу придумать, как вам это проиллюстрировать!
Формула вершин– Что такое формула вершин? Примеры
Формула вершины параболы используется для нахождения координат точки, в которой парабола пересекает свою ось симметрии. Вершиной является точка (h, k). Как мы знаем, стандартное уравнение параболы: y = ax 2 + bx + c.Если коэффициент x 2 положительный, то вершина является нижней частью U-образной кривой, а если он отрицателен, вершина является вершиной U-образной кривой. Вершина, в которой парабола минимальна (когда парабола открывается) или максимальна (когда парабола открывается вниз) и парабола поворачивается (или) меняет свое направление. Давайте узнаем больше о формуле вершины и решим примеры.
Что такое формула вершин?
Формула вершины помогает найти координаты вершины параболы.Стандартная форма параболы: y = ax 2 + bx + c. Вершинная форма параболы y = a (x – h) 2 + k. Есть два способа определить вершину (h, k). Их:
- (h, k) = (-b / 2a, -D / 4a), где D (дискриминант) = b 2 – 4ac
- (h, k), где h = -b / 2a, и вычислим y в h, чтобы найти k.
Вершинная формула
Две формулы вершины для нахождения вершины:
Формула 1: (h, k) = (-b / 2a, -D / 4a)
где,
- D – знаменатель
- h, k – координаты вершины
Формула 2: Координата x вершины = -b / 2a
Вывод формул вершин
Формула 1
Мы знаем, что стандартная форма параболы: y = ax 2 + bx + c.Преобразуем его в форму вершин y = a (x – h) 2 + k, заполнив квадраты.
Вычитая c с обеих сторон:
у – с = ах 2 + bx
Принимая “а” в качестве общего множителя:
у – с = а (х 2 + б / а х)
Здесь половина коэффициента при x равна b / 2a, а его квадрат равен b 2 / 4a 2 . Сложение и вычитание справа (в скобках):
y – c = a (x 2 + b / a x + b 2 / 4a 2 – b 2 / 4a 2 )
Мы можем записать x 2 + b / a x + b 2 / 4a 2 как (x + b / 2a) 2 .Таким образом, приведенное выше уравнение становится:
y – c = a ((x + b / 2a) 2 – b 2 / 4a 2 )
Распределяя “а” с правой стороны и добавляя “с” с обеих сторон:
y = a (x + b / 2a) 2 – b 2 / 4a + c
y = a (x + b / 2a) 2 – (b 2 – 4ac) / (4a)
Сравнивая это с y = a (x – h) 2 + k, получаем:
h = -b / 2a
к = – (b 2 – 4ac) / (4a)
Мы знаем, что b 2 – 4ac – дискриминант (D).
Таким образом, формула вершины: (h, k) = (-b / 2a, -D / 4a) , где D = b 2 – 4ac
Формула 2
Если вам трудно запомнить приведенную выше формулу, вы можете просто запомнить формулу для координаты x вершины, а затем просто подставить ее в данное уравнение y = ax 2 + bx + c, чтобы получить координату y вершины вершина.
Координата x вершины (h) = -b / 2a
В качестве альтернативы, если вы не хотите использовать какую-либо из приведенных выше формул для поиска вершины, вы можете просто заполнить квадрат для преобразования y = ax 2 + bx + c формы y = a (x – h) 2 + k вручную и найдите вершину (h, k).
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Примеры использования формулы вершин
Пример 1. Найдите вершину y = 3x 2 – 6x + 1.
Решение:
Найти: вершину данного уравнения (параболы).
Сравнивая данное уравнение с y = ax 2 + bx + c, получаем
a = 3, b = -6, c = 1.
Тогда дискриминант D = b 2 – 4ac = (-6) 2 – 4 (3) (1) = 36-12 = 24.
Используя формулу вершин (формула 1),
Вершина, (h, k) = (-b / 2a, -D / 4a)
(ч, k) = (- (- 6) / (2 × 3), -24 / (4 × 3)) = (6/6, -24/12) = (1, -2)
Следовательно, вершина данной параболы = (1, -2).
Пример 2: Найдите вершину параболы, пересечения по оси x которой равны (2, 0) и (3, 0), а пересечение по оси Y – (0, 6).
Решение:
Найти: вершину данной параболы.
Поскольку (2, 0) и (3, 0) являются пересечениями x данной параболы, (x – 2) и (x – 3) являются множителями уравнения параболы. Итак, уравнение параболы имеет вид:
у = а (х – 2) (х – 3) …. (1)
Его точка пересечения по оси y задается равной (0, 6). Подставляем x = 0 и y = 6 в приведенное выше уравнение:
6 = а (0 – 2) (0 – 3)
6 = 6a
а = 1
Заменить a = 1 в (1):
y = 1 (x – 2) (x – 3) = x 2 – 5x + 6… (2)
Сравнивая приведенное выше уравнение с y = ax 2 + bx + c, получаем
а = 1; b = -5; с = 6
Используя формулу вершин (формула 2),
Координата x вершины = -b / 2a = – (- 5) / (2 × 1) = 5/2
Подставьте это в (2), чтобы найти y-координату вершины.
y = (5/2) 2 – 5 (5/2) + 6 = -1/4
Следовательно, Вершина данной параболы = (5/2, -1/4)
Пример 3: Определите координаты вершины для данного уравнения параболы: y = 4x 2 + 16x -16
Решение:
Данное уравнение: y = 4x 2 + 16x -16
Здесь a = 4, b = 16
Мы знаем, что формула для определения координаты x задается как -b / 2a
= -16/2 (4)
= -2
Следовательно, координата x равна -2
.Теперь подставляем значение x в данное уравнение, получаем
у = 4 (-2) 2 +16 (-2) -16
г = -32
Следовательно, координаты вершины (h, k) равны (-2, -32)
перейти к слайду перейти к слайду
Часто задаваемые вопросы о Vertex Formula
Что такое формула вершин?
Формула вершины параболы используется для нахождения координат точки, в которой парабола пересекает свою ось симметрии.Координаты задаются как (h, k). Вершиной параболы является точка, в которой парабола минимальна (когда парабола открывается) или максимальна (когда парабола открывается вниз), и парабола поворачивается (или) меняет свое направление.
Какова формула поиска вершины по координатам X?
Используя стандартную форму параболы y = ax 2 + bx + c и уравнение вершин y = a (x – h) 2 + k, мы можем получить первую формулу вершины, т.е.
Формула вершины: (h, k) = (-b / 2a, -D / 4a) , где D = b 2 – 4ac
Как использовать формулу вершин?
Формула вершины может использоваться, чтобы найти вершину любой параболы, используя уравнение параболы.Формула вершины для уравнения параболы y = ax 2 + bx + c задается как, (h, k) = (-b / 2a, -D / 4a) , где D = b 2 – 4ac
Какова формула поиска вершины в координатах Y?
Чтобы найти вершину (h, k), получите h (x-координата вершины) = -b / 2a из стандартного уравнения y = ax 2 + bx + c, а затем найдите y в h, чтобы получить k ( координата y вершины).
Какая альтернативная формула используется для поиска вершины?
Формула вершины для нахождения координат вершины (h, k) = (-b / 2a, -D / 4a) из стандартного уравнения y = ax 2 + bx + c, где D = b 2 – 4ac.
Построение линейного уравнения с помощью таблицы значений
Построение графика линейного уравнения
Линейное уравнение – это уравнение с двумя переменными, которое при построении графика дает нам прямую линию. Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг – научиться составлять таблицу значений.
Что такое таблица значений
Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений.Таблица значений, как следует из названия, представляет собой графический способ определения значений, которые будут использоваться для создания вашего графика. Это место, где вы можете записать ответы, которые вы получите, когда найдете значения x и y. Для построения линейного уравнения вам понадобится как минимум 2 набора точек, но обычно вы можете сделать больше в таблице значений.
Таблица значений состоит из двух столбцов. В одном столбце перечислены значения x, а в одном столбце – соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.
Построение линейных уравнений с помощью таблицы значений
Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите построить графиком, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y. Представим, что у вас -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.
Выберите другое значение x, с которым вы хотите работать, и снова решите относительно y. Повторите столько раз, сколько хотите, чтобы выработать наборы значений для включения в вашу таблицу. Когда у вас есть сумма, которая вас устраивает или которую требует ваш вопрос, вы можете затем взять эти значения x и y и нанести их в виде координат на график, чтобы обозначить точки на линейном уравнении!
Примеры задач
Вопрос 1:
График следующей функции с использованием таблицы значений
у = 3х – 1
Решение:
Сначала создайте таблицу значений для уравнения.Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одним и тем же независимо от того, какие значения вы используете.
Таблица значений xДля x = -2
у = 3 (-2) – 1
г = -6 – 1
г = -7
Для x = -1
у = 3 (-1) – 1
г = -3 – 1
г = -4
Для x = 0
у = 3 (0) – 1
г = 0 – 1
г = -1
Для x = 1
у = 3 (1) – 1
г = 3 – 1
г = 2
Для x = 2
у = 3 (2) – 1
г = 6 – 1
г = 5
Теперь у нас есть полная таблица значений
Заполненная таблица значений x и yТеперь мы можем нанести упорядоченные пары на сетку
Построение данныхЗатем соедините точки прямой линией, и готово!
Связывание данных по прямойВопрос 2:
Изобразите следующую функцию, используя таблицу значений:
2x + 4y = 8
Решение:
Во-первых, мы хотим упростить уравнение
2x + 4y = 8
х + 2у = 4
2у = -x + 4
y = −12 \ frac {-1} {2} 2−1 x + 2
Теперь у нас есть уравнение в форме пересечения наклона.
Затем создайте таблицу значений для уравнения. Используйте x, чтобы найти y.
Таблица x решает для yДля x = -2
y = −12 \ frac {-1} {2} 2−1 (-2) + 2
у = 1 + 2
г = 3
Для x = -1
y = −12 \ frac {-1} {2} 2−1 (-1) + 2
у = 0,5 + 2
г = 2,5
Для x = 0
y = −12 \ frac {-1} {2} 2−1 (0) + 2
у = 0 + 2
г = 2
Для x = 1
y = −12 \ frac {-1} {2} 2−1 (1) + 2
у = -0.5 + 2
г = 1,5
Для x = 2
y = −12 \ frac {-1} {2} 2−1 (2) + 2
у = -1 + 2
г = 1
Теперь у нас есть полная таблица значений
Таблица заполненных данныхМы можем нанести упорядоченные пары на сетку.
Координаты, построенные с использованием таблицы данныхЗатем соедините точки прямой линией, и готово!
Свяжите данные вместе прямой линиейХотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот для справки онлайн-калькулятор.
Далее, узнайте больше о таблице значений, как построить график линейных неравенств с двумя переменными и как построить график систем линейных неравенств. Вы также можете начать изучать введение в функции и способы их определения.
Таблица функций (2 переменные) Калькулятор
- Цель использования
- Чтобы создать функцию для скрипт Python, в котором он обратный отсчет в обратном порядке в каждом столбце по строкам.
- Комментарий / запрос
- Очень полезно, спасибо!
[1] 2021/09/30 02:34 Уровень 20 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- попытка найти функцию с помощью таблицы без уравнения
[2] 2021/09/09 09:32 До 20 лет / Старшая школа / Университет / аспирант / Немного /
- Цель использования
- Назначение функций
[3] 2021/08/16 19:58 Моложе 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Мне нужно было найти шаблон для [более сложных] линейных функций, чтобы быстро двигаться дальше с уравнениями быстрее / подробнее точно
- Комментарий / запрос
- что-то более четкое
[4] 2021/07/ 02 18:54 До 20 лет / Старшая школа / Университет / Аспирант / Не совсем /
- Цель использования
- Чтобы найти уравнение с таблицей
- Комментарий / Запрос st
- Указания должны быть более точными, и должно быть больше вариантов, если мы хотим уравнение или что это такое.
[5] 2021/05/03 18:18 Моложе 20 лет / Начальная школа / Младший школьник / Не совсем /
- Цель использования
- Чтобы мои расчеты выполнялись быстрее при выполнении домашних заданий.
[6] 2021/04/27 20:25 Моложе 20 лет / Средняя школа / Университет / аспирант / Не совсем /
- Цель использования
- Завершить таблицу с математической таблицей парабол
- Комментарий / Запрос
- Меньше требований к калькулятору, я хочу найти y не выражение
[7] 2021/04/25 15:22 Моложе 20 лет / Начальная школа / Младший старшеклассник / Не совсем /
- Цель использования
- Нужна помощь с домашним заданием по математике.
- Комментарий / запрос
- Требуется уравнение таблицы функций.
[8] 2021/04/20 17:30 Меньше 20 лет / Начальная школа / Младший школьник / Немного /
- Цель использования
- Просто практика
- Комментарий / Запрос
- Мне нужно чтобы определить, какая функция (линейная, квадратичная или экспоненциальная) функционирует из таблиц.
[9] 2021.03.18 15:58 До 20 лет / Начальная школа / Неполная средняя школа / Немного /
