Что показывает вольтметр: Что показывает вольтметр, или математика розетки / Хабр

Автомобильный вольтметр – для чего нужен и как подкючить

От работы электрооборудования зависит работа всего автомобиля, ведь при неисправности электрики автомобиль может потерять способность двигаться. Спрогнозировать такой отказ поможет вольтметр.

Автомобили давно уже стали настолько надежными, что конструкторы отказались от многих контрольных приборов. И пока машина молодая, это не вызывает у водителя проблем. Но когда у нее за плечами десяток-полтора лет, даже самые продуманные системы могут отказать.

Вольтметр, как и некоторые другие индикаторы, автопроизводители уже не ставят в панель приборов

И, вероятно, самое слабое место в неновой машины – ее электрооборудование. Периодический контроль напряжения в бортовой сети помогает спрогнозировать серьезные неприятности с бортовой энергетикой – и предотвратить их. Для этого нужен несложный прибор – вольтметр.

ЧИТАЙТЕ ТАКЖЕ: Новые вопросы об АКБ: как ухаживать за аккумулятором

Сегодня предлагается немало вариантов крепления вольтметров для автомобиля: в гнездо прикуривателя, сверху на торпедо, непосредственно в панель

Купить вольтметр для автомобиля сегодня не проблема, эти приборы предлагаются на разных площадках, от рынка-барахолки до интернет-магазинов. В техническом плане есть как минимум два варианта: либо старый добрый аналоговый прибор со стрелкой, либо современный электронный, с цифровой индикацией. Первые более надежные, вторые более удобны с точки зрения размещения в салоне.

Как установить вольтметр в салоне

• Подключение должно обеспечивать измерение напряжения в сети, в том числе и когда все потребители отключены;
• Прибор не обязательно располагать на виду, ведь контроль нужен лишь периодический;
• Обязательно позаботьтесь, чтобы провода, идущие к вольтметру, были надежно защищены от повреждений и замыкания на массу автомобиля;
• В идеале вольтметр должен быть подключен непосредственно к клеммам аккумулятора, ведь важнее всего контролировать напряжение именно на нем;
• Самым удобным местом для подключения вольтметра обычно бывает розетка прикуривателя, и это вполне приемлемый вариант;
• Если вы не уверены в том, что сможете безопасно подключить вольтметр, обратитесь к профессиональному электрику.

Стрелочные приборы порой кажутся старомодными, но с них легче считывать информацию

Как пользоваться вольтметром в машине

С помощью вольтметра можно делать выводы о состоянии аккумулятора, работе генератора и состоянии проводки на самых важных участках. Например, напряжение на клеммах аккумулятора при всех выключенных потребителях (так называемое напряжение разомкнутой цепи) должно составлять не менее 12,6 вольт. Если меньше – АКБ либо недозаряжена (надо подзарядить от стационарного устройства), либо нуждается в замене из-за возраста.

ЧИТАЙТЕ ТАКЖЕ: Какой аккумулятор купить для автомобиля: 5 параметров выбора

Работу генератора проверить немного сложнее – нужно контролировать показания вольтметра на разных оборотах двигателя при максимальном количестве включенных потребителей. На оборотах холостого хода под нагрузкой напряжение может приближаться к напряжению аккумулятора (12,6 – 12,8), на средних оборотах желательно видеть стрелку прибора около 13,5 вольт.

В принципе, если вам не хочется с помощью вольтметра и вышеприведенных рекомендаций превратиться в такого себе бортинженера, посоветуем более простой вариант. Просто время от времени следите за показаниями прибора:

1. При заглушенном двигателе и всех выключенных потребителях энергии напряжение должно быть не ниже 12,6 В;
2. При работающем двигателе и включенных фарах, обогреве стекла и стоп-сигналах показания должны укладываться в диапазон 12,8 – 14,5 В.

Если показания будут отличаться от указанных, обратитесь к электрику.

Вольтметры, которые выполнены более или менее профессионально, нуждаются в участии специалиста при инсталляции в автомобиль

В некоторых современных автомобилях в недрах меню борткомпьютера можно найти показания напряжения в бортовой сети. Также помогают следить за напряжением аккумулятора некоторые охранные системы с имеющих GSM-модуль для управления со смартфона. Конечно, если такие опции есть, то устанавливать дополнительный прибор не стоит.

Рекомендация Авто24

Для более или менее свежего автомобиля наличие вольтметра на борту необязательно. Но если вы покупаете себе в салон какой-то электронный девайс типа дополнительного термометра, тахометра или часов, имейте в виду, что иногда такие приборы имеют и функцию вольтметра. Поэтому не пожалейте денег на прибор именно с таким функционалом – доплата будет небольшой, а энергосистема автомобиля может постареть неожиданно.

НАПОМНИМ, ЧТО означают значки на панели приборов.

№ 1279 ГДЗ Сборник задач по физике 7-9 класс Лукашик. Что показывает вольтметр? – Рамблер/класс

№ 1279 ГДЗ Сборник задач по физике 7-9 класс Лукашик. Что показывает вольтметр? – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?

Помогите определить!
Для определения сопротивления электрической лампы ученица составила цепь (рис. 313). При замкнутой цепи амперметр показывает 0,5 А. Что показывает вольтметр? Чему равно сопротивление лампы?
 
 

ответы

Привет. Помогу

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

№ 179 Сборник задач по физике 7-9 класс Лукашик. Почему патрон продолжает вращаться?

У кого есть ответ?
Почему после выключения двигателя сверлильного станка патрон продолжает вращаться?
 

ГДЗФизика7 класс8 класс9 классЛукашик В.И.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим.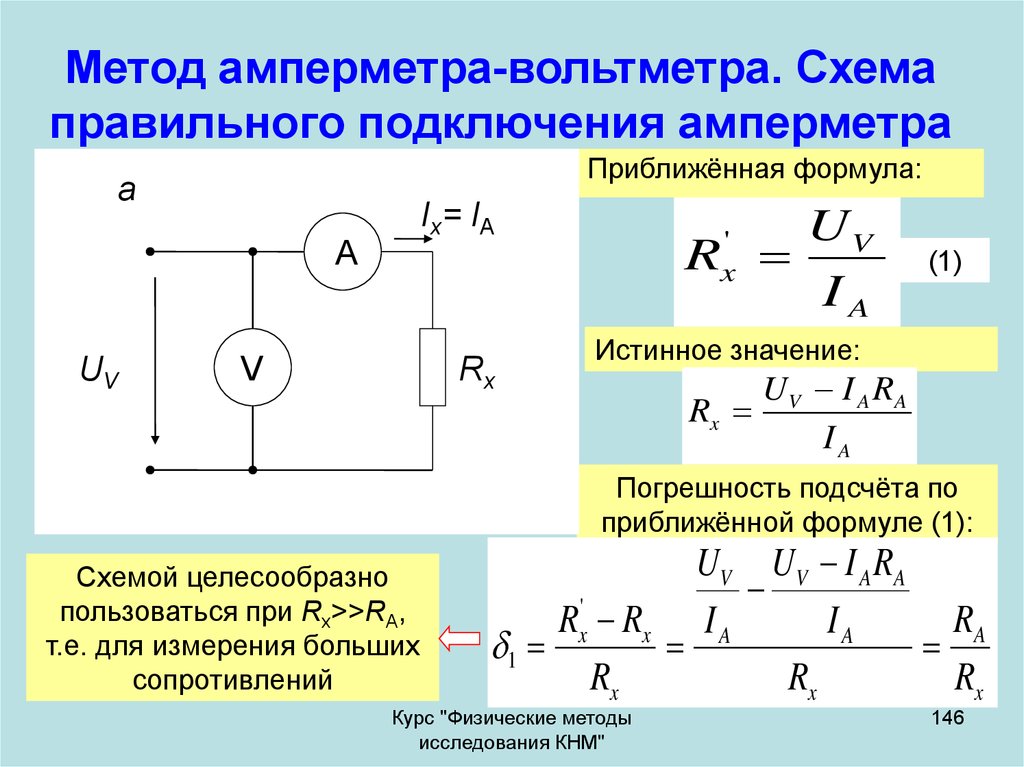 практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора

сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион.

Срочно!

ГИА9 класс

Напряжение

. Что измерил бы вольтметр, если бы у вас была электродвижущая сила, создаваемая изменяющимся магнитным полем?

Если переменное магнитное поле заключено внутри треугольника, то (высокоомный) вольтметр, расположенный вне треугольника, как вы его изобразили, будет измерять напряжение, равное R * I, где I — ток, протекающий в петле I = ЭДС / (Р + Р + Р).

И он будет последовательно считывать это значение, независимо от того, как расположены датчики, скручены, раскручены, закручены, длинные или короткие – до тех пор, пока датчики остаются вне области переменного магнитного поля (то есть вне треугольника), не вокруг него не ходят круги и нет переменных магнитных полей вне области внутри треугольника.

Чтобы проиллюстрировать, почему это так, я буду использовать без ограничения общности более простую схему всего с двумя резисторами, которую я назову кольцом Ромера-Левина.

_{Ключ к пониманию того, что означает «вольтметр с одной стороны», заключается в том, как вы переходите от плюса к минусу через щупы, в одном случае по часовой стрелке, в другом против часовой стрелки (обратите внимание, что это отрицательный эскиза на бумаге, поэтому положительный вывод пустой, а отрицательный – заполненный)}

Следующий рисунок еще более поразителен: если вы ограничиваете скольжение щупов по кольцу и вам не разрешено отсоединять наконечники, вы можете двигать наконечники вдоль кольца, чтобы коснуться клемм резистора на другой стороне и прочитать то же самое. напряжение

Это можно объяснить либо рассмотрением того, как две сетки, содержащие вольтметр (одна с большим резистором, а другая с маленьким резистором), усугубляют эффекты, либо рассмотрением индуцированных вокруг поля dB/dt.

Я также дал длинное объяснение того, как работает подобное расположение с точки зрения поля total

внутри кольца, в этом ответе мне пришлось сократить его, так как я достиг 30 тысяч символов. Все ключевые моменты приведены в начале этого ответа. Применительно к вашей схеме могу констатировать следующее:

• Напряжение четко определено, зависит только, в общем от тракта.
• Разность потенциалов больше не определяется.
• Область переменного поля в основном создает индуцированное электрическое поле, особенностью которого является консервативность в односвязных областях, не содержащих треугольник. (Это можно довольно элегантно показать, если мы предположим, что переменное магнитное поле равномерно возрастает и ограничено цилиндрической симметричной областью пространства, в основном создаваемой бесконечно длинным соленоидом)
• Итак, все закрытые пути, находящиеся снаружи треугольника (при условии, что переменное магнитное поле ограничено там) и не заключайте его, даст интеграл по путям от E, равный ноль, и KVL будет отлично работать с сетками, которые следуют за этими пути.
• Ваша схема, однако, не является таким путем, так как она идет вокруг переменного магнитного поля, и интеграл по путям не будет ноль, а будет даваться по закону Фарадея. Следовательно, КВЛ умирает (из ужасная и невосстановимая смерть) в вашей цепи.

Экспериментальная установка

Вы можете проверить приведенные выше утверждения с достаточно большим тороидальным трансформатором и тремя резисторами, припаянными кольцом вокруг сердечника. Я говорю «достаточно большой», потому что суть в том, что вы не сможете «сгруппировать» переменную область в изолированной части вашей схемы. Убедитесь, что резисторы не «видят» друг друга из-за того, что на пути находится сердечник (причина этого будет объяснена позже). Что-то вроде этого:

_{На этом рисунке часть ядра не показана, чтобы сделать видимыми линии поля. Я использую слово «трансформатор», потому что я провел эксперимент с тороидальным трансформатором.}

Для простоты, поскольку у меня уже есть много иллюстраций, иллюстрирующих супердемонстрацию Левина, и поскольку основная физика точно такая же, в дальнейшем я буду использовать круглое кольцо только с двумя резисторами. Это имеет два основных преимущества: во-первых, оно не отвлекает от реальной цели эксперимента, т. е. демонстрирует, что напряжение зависит не только от конечных точек, но и от пути, по которому вам нужно его оценить; и, во-вторых, симметрия упростит математику до такой степени, что мы сможем найти фактические задействованные поля с относительно небольшими усилиями.

Из комментариев я вижу, что вас интересуют «строки поля возврата» поля B. Что ж, тороидальная установка в основном ограничивает почти все линии внутри ядра, так что вам не придется сильно беспокоиться об их перехвате вашими зондами. Левин использует длинный соленоид, который является аппроксимацией бесконечно длинного соленоида, силовые линии которого замыкаются на бесконечности, например

. Если соленоид не такой длинный, то надо быть осторожнее с обраткой. Вот почему Левин помещает кольцо с резистором близко к соленоиду в области, где он ранее измерил поле, чтобы показать, что оно было незначительным. Мехди, с другой стороны, не так осторожен и использует очень короткий соленоид с гайкой или болтом в качестве сердечника.

Это неразумный выбор, потому что он добавляет ненужные сложности, связанные с необходимостью скручивания линий зонда, чтобы избежать связывания потока , возвращающего . И может привести его зрителей к мысли, что такое искажение является ключом к тому, чтобы избежать предполагаемой «ошибки исследования» Левина.

О возбуждении
Поскольку мы говорим об экспериментальной установке, было бы полезно сказать несколько слов о том, что заставляет цепь работать: то есть, как быстро меняется магнитное поле. В случае электрически стимулируемого источника — либо с помощью первичной катушки, либо с помощью электромагнита — у нас есть несколько возможностей 9.0003

• Синусоидальное возбуждение
  используется в демонстрации 10 Массачусетского технологического института, Haus & Melcher, Purcell. Я использовал это, чтобы воспроизвести эксперимент самостоятельно. мы можем легко вычислить скорость изменения и оценить, должны ли мы беспокоиться о собственной индуктивности кольца
• Импульс с затуханием
  , использованный Левином и Мехди — нам может понадобиться вычислить, как быстро нарастает и спадает поле.
• Линейно возрастающее и насыщающее поле
  , использованное Левином в короткометражном видео «КВЛ для птиц» (предупреждение: в этом видео Левин вольно использует слово «потенциальная разница», которое, на мой взгляд, является единственным критиком, которого я могу коснуться). к его изложению. Я бы употребил слово «напряжение», указав путь)
• Часть треугольной волны
  , используемая Ромером – это в основном делает ток в кольце прямоугольной волной, следовательно, примерно постоянной почти для всех полупериодов

Во всех приведенных выше сценариях мы можем выбрать возбуждение настолько медленным, что собственная индуктивность и ее влияние будут пренебрежимо малы (в последних двух, в интервалах, где поле линейно нарастает, а напряжение постоянно, само понятие собственного индуктивность убита в кредле). Частота или время возбуждения и возникающих напряжений и токов таковы, что нам не нужно беспокоиться о распределенных эффектах или замедлении. Кольцо не является ни линией передачи, ни антенной.

Далее я попытаюсь нарисовать картину индуцированного поля, которая, надеюсь, объяснит, почему вы получаете стабильные результаты за пределами кольца (в схеме Левина и тороидальной установке, а не в том, что гайки и болты путаются).

В дальнейшем я буду предполагать, что магнитное поле в плоскости кольца пространственно однородно внутри круглой области с тем же центром, что и кольцо, и однородно (в идеале бесконечно, на практике на время эксперимента) увеличение. Это приведет к постоянным значениям тока и напряжения.

Наведенное электрическое поле

Можно показать, что наведенное электрическое поле создается пространственно-однородным переменным во времени магнитным полем соленоида круглого сечения (либо бесконечно длинным и линейным, либо замкнутым на себя, как в тороидальном трансформаторе), или даже электромагнита, приводимого в движение переменным током, направлена ​​по концентрическим линиям и растет как расстояние r от центра сечения внутри области магнитного поля, но уменьшается как 1/r вне ее.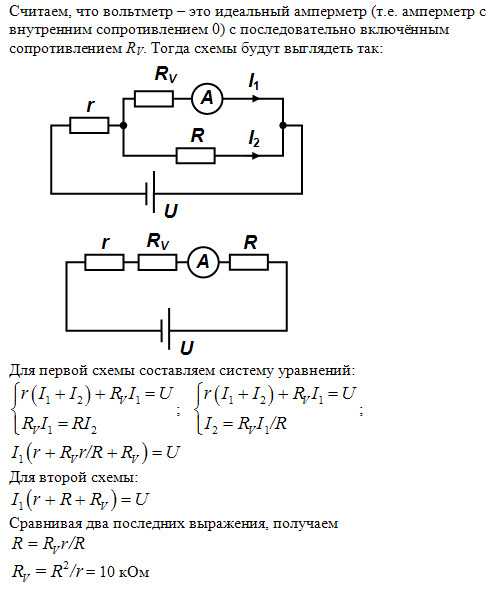 На следующем рисунке оранжевое кольцо радиуса R обозначает границу зоны однородного переменного магнитного поля. Поле В считается пространственно однородным и перпендикулярным плоскости кольца, а направление индуцируемого электрического поля зависит от направления В, но, что наиболее важно, от знака скорости его изменения.

_{Emax — максимальное значение, которое может достигать индуцированное поле, и оно достигается прямо на границе с магнитной областью. Если вы используете тороидальный трансформатор, питаемый синусоидальным током, и находитесь на расстоянии r>R, то вы увидите косинусоидальное переменное электрическое поле, пропорциональное Ep cos wt и всегда направленное по окружности. Стрелка электрического поля то увеличивается, то уменьшается, меняет направление и увеличивается в противоположном направлении}

Симметрия играет доминирующую роль в поиске решения, и вы можете найти доказательства в большинстве книг по физике и ЭМ, например, у Оганяна, “Физика” 2e с. 791 для длинного соленоида и об Оганяне, “Физика для инженеров и ученых” 3д с. 1006 для электромагнита. Для нас важно то, что (для круговой магнитной области радиуса R) в данный момент времени t:

• \$E_{ind}\$ пропорционально \$r\$ при \$r\leq R\ $
• \$E_{ind}\$ пропорционально \$1/r\$ для \$r \geq R\$

Обратите внимание, что в процессе вычисления ЭДС и поля относительно заданного пути мы рассматриваем только геометрические, математические, эфирные пути. Здесь еще нет материи: когда вы помещаете материю внутрь индуцированного поля, электроны будут реагировать и перераспределяться, нарушая исходное поле и изменяя его таким образом, что это будет полное результирующее поле. К счастью, мы можем использовать суперпозицию, чтобы найти окончательный результат.

Закрытые пути и обратимость
Перед тем, как приступить к делу, давайте посмотрим, что означает эта конфигурация индуцированного поля для особого вида траекторий (опять же, математических траекторий) внутри и вне области магнитного поля. Посмотрите на эти два круглых (усеченных) сектора: они состоят из двух радиальных частей и двух круглых частей. Теперь давайте вычислим ЭДС вдоль этих путей, вычислив линейный интеграл индуцированного поля (единственное поле, присутствующее здесь)

Индуцированное поле перпендикулярно радиальным путям, поэтому оно не будет вносить в них никакого вклада. А круглые детали? Ну, так как поле направлено по окружности, вклад будет полным: \$E_{ind}\$ и dl параллельны, поэтому их скалярное произведение будет произведением их величин. Каждый круговой сегмент будет вносить \$E_{ind}(r)\$, умноженный на длину пути. Длина пути для этих круговых сегментов будет расти как r (обратите внимание, что для одного и того же пути они оба образуют один и тот же угол).

Теперь вне области магнитного поля \$E_{ind}(r)\$ растет как \$1/r\$, а длина пути растет как \$r\$, так что интеграл по пути вдоль этих отрезков будет идентичны (в одном у вас сильное поле на коротком расстоянии, в другом слабое поле на большем расстоянии). Но их знак будет обратным, так как в одном случае поле \$E_{ind}\$ будет идти по пути, а в другом – против него. Конечным результатом является то, что интеграл по этим путям будет равен нулю. ЭДС в них не индуцируется. И этого следовало ожидать, поскольку они не связывают и область переменного магнитного поля. (другая история относится к траекториям усеченных секторов внутри магнитной области, но в этом посте они нас не интересуют)

Теперь эту особенность замкнутых секториальных траекторий вне области магнитного поля можно обобщить на траектории любой формы, которые не охватывают зону dB/dt: просто разложите их на радиальные и тангенциальные сегменты, чтобы показать, что это так. Получается, что индуцированное электрическое поле в конце концов ведет себя как консервативное поле.

Но, подождите! Что произойдет, если мы не будем включать «компенсирующую дугу», идущую в противоположном направлении? Мы можем сделать это, обогнув область переменного магнитного поля, вот так

В этом случае путь ДЕЙСТВИТЕЛЬНО связывает и ЭДС, и это всегда одна и та же ЭДС, независимо от формы и размера пути. В любом случае это не то, что сделала бы консервативная область.

Итак, играя с векторами, мы пришли к выводу, что индуцированное электрическое поле ведет себя как консервативное поле в каждой части пространства, НЕ ВКЛЮЧАЮЩЕЙ область переменного магнитного поля. Область пространства, где индуцированное поле ведет себя как консервативное поле, имеет дыру.

Предварительный просмотр: Эта «дыра в пространстве консервативности» является причиной того, что кольцо Левина невозможно объединить: поместив резисторы на противоположных сторонах кольца, Левин создал цепь , путь которой нельзя сократить до точки , как вы потребуется в нульмерном приближении теории цепей с сосредоточенными параметрами. Таким образом, нет возможности включить влияние переменного магнитного поля в сосредоточенные компоненты, например, используя взаимные индуктивности вместо двух отрезков проводов, соединяющих резисторы (или четыре взаимных индуктивности, если вы хотите изолировать точки A и B на полпути). ), потому что вы не можете исключить область переменного поля из пути схемы.

_{Геометрия имеет значение. Схема Левина требует, чтобы два резистора находились на противоположных сторонах «дыры в консервативности», которая является областью переменного магнитного поля. Вы не можете растянуть путь цепи, заставив часть с резисторами сжаться в точку (представьте, что резисторы тоже являются точками), как того требует теория сосредоточенных цепей, без потери этого геометрического ограничения. Это делает кольцо Левина неразложимым .
В смешанных схемах, с другой стороны, геометрия схемы не имеет значения (она может иметь значение внутри компонентов, но мы не должны открывать их, чтобы заглянуть внутрь)}

Конечно, можно поставить оба резистора на одну сторону и представить, что оставшийся проводник — это вторичная обмотка трансформатора, но это будет другая схема, неравномерная, со скачком напряжения, которого нет в кольце Левина.

Просто наденьте на него кольцо

Далее я поставлю кольцо с двумя его резисторами внутрь поля и посмотрю, что произойдет.

эта часть будет продолжена в ближайшее время. Мне нужно отформатировать уравнения. Нет, у меня больше нет места.

Сказка о двух полях

Если мы примем явно разумное предположение, что ток в кольце не изменяет магнитное поле B заметным образом (вы можете вычислить поле, связанное с 1 мА, по скорости изменения, подразумеваемой частоту или время, если хотите), мы можем заключить, что колумбово электрическое поле \$E_c\$, создаваемое зарядом, накопленным на конце резисторов, не изменит индуцированное поле \$E_{ind}\$, которое сохраняет свою независимость от того, что происходит на ринге и вокруг него. Таким образом, в кольцевом эксперименте Ромера-Левина полное поле представляет собой суперпозицию двух полей: независимого индуцированного поля (это означает, что оно вызвано только возбуждением и не зависит от всего, что происходит в кольце) и колумбового поля, создаваемого заряды, смещенные указанным индуцированным полем.

\$E_{tot} = E_{ind} + E_c\$

Последнее представляет собой консервативное безвихревое поле, допускающее потенциальную функцию. Для этой парциальной составляющей полного электрического поля мы можем определить разность потенциалов, которая не зависит от путей, а зависит только от конечных точек. Это «уникальная разность потенциалов», которая, по мнению некоторых сторонников «KVL всегда держится», невосприимчива к (несуществующим) ошибкам зондирования. Ну, это не так. Это только половина истории, и в этом нет ничего нового: у Гельмольца есть теорема его имени, которая говорит нам, что любое векторное поле (при разумном поведении) может быть разложено на его безвихревые и вращательные компоненты. их компонентов и как таковое общее поле представляет собой… состав двух.

Это соленоидальные и консервативные компоненты полного электрического поля внутри и вокруг кольца Ромера-Льюина

_{Примечание: в эксперименте два кольца. (Слева) Кольцо соленоида (или след электромагнита) ограничивает границу области переменного магнитного поля. Эта область полностью содержится внутри большего кольца Ромера-Левина с двумя резисторами (справа). Полное поле Etot является суммой электрического поля Eind, индуцированного dB/dt, и колумбового поля Ec, обусловленного смещенным зарядом в кольце с резисторами.}

Их легко определить благодаря исключительной симметрии установки. Тот факт, что кольцо с резистором круглое и центрировано вокруг соленоида, устраняет необходимость в зарядах боковой поверхности для управления колумбовым полем внутри окружности кольца. Поле, показанное справа, было рассчитано с двумя парами противоположных зарядов в соотношении 9:1, чтобы представить заряд на клеммах резисторов 900 Ом и 100 Ом. Обратите внимание, даже при таком грубом приближении стрелки поля \$E_c\$ следуют круговому профилю оранжевого кольца в направлении, противоположном полю \$E_{ind}\$.
В идеальном проводнике это тангенциальное поле \$E_c\$ полностью уничтожит противоположное тангенциальное поле \$E_{ind}\$, оставив внутри проводников нулевое электрическое поле.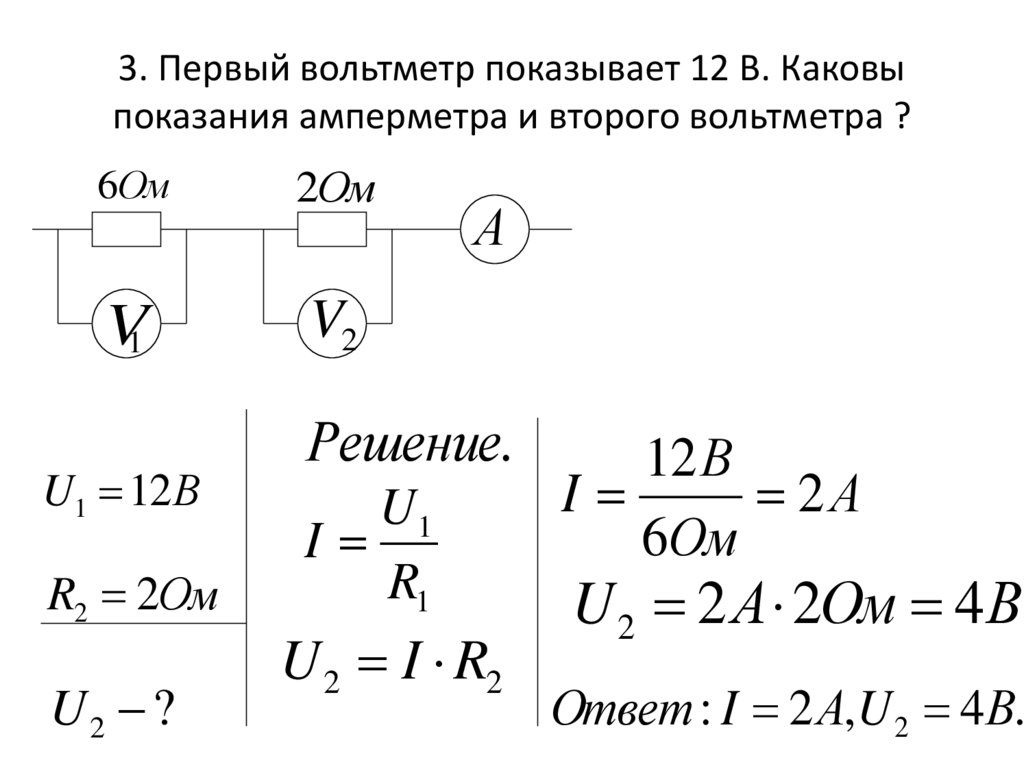 В меди, учитывая очень высокую проводимость, будет очень малое результирующее электрическое поле \$E_{tot}\$, совместимое с законом Ома: \$E_{tot} = j / \sigma_{copper}\$

В реальном мире, где такой симметрии нет, потому что соленоид и кольцо не центрированы и/или формы не идеально круглые, на проводнике и резисторе возникнет заряд боковой поверхности (подробнее об этом можно прочитать в моем ответе на «Постоянно ли электрическое поле в проводе»), но это не меняет полного поля внутри кольца, которое мы можем представить следующим образом:

Это, в конце концов, то, что имеет значение: окончательная конфигурация ОБЩЕГО электрического поля внутри кольца. И что мы видим здесь, так это то, что БЕЗ КАКИХ-ЛИБО ЗОНДОВ мы имеем (по крайней мере) два разных пути, соединяющих точки B и A, которые имеют разные конфигурации полного электрического поля \$E_{tot}\$. Если мы перейдем от B к A вдоль большего резистора RH, интеграл пути, который представляет напряжение, даст нам значение 0,9 В, более положительное в B; если мы пройдем от В к А (ТЕ ЖЕ ТЕ ЖЕ ДВЕ ТОЧКИ) по меньшему резистору RL интеграл по пути даст нам напряжение 0,1В, более положительное в А.

Напряжение на тех же самых двух точках может иметь (как минимум) два разных значения одновременно. А это не ошибка зондирования потому что НЕТ ПРОБ XXXXXXXX! (Извините, но мне очень-очень нужно было выговориться. Это было адресовано не вам, а всем тем инженерам, которые сардонически улыбались Левину).
Более того, «распределенной ЭДС» по кольцу нет: индуцированное поле «израсходовано» на создание того самого распределения заряда, которое почти полностью стирает его в проводнике. Единственный оставшийся след ЭДС — это падение напряжения на резисторах. «Магнитная ЭДС», вытекающая из закона Фарадея, в кольце, так сказать, невидима.

Закон Фарадея — это новый закон физики, по праву занявший свое место среди уравнений Максвелла, поскольку он устанавливает фундаментальное свойство электромагнитного поля, когда поля изменяются во времени. Он представляет собой полный прорыв, изменивший то, как мы видим электромагнитные поля в квазистатических условиях (и, наряду с добавлением члена смещения в закон Ампера-Максвелла, также и в электродинамике в целом). Есть причина, по которой rot E = -dB/dt не называется ‘ обобщил закон Кирхгофа ‘. Это нечто совершенно новое, и попытка объединить его с «просто новым видом ЭДС для вычисления при использовании КВЛ» является оскорблением памяти Фарадея.

Одна петля, две петли, три петли…

И, наконец, давайте посмотрим, как с помощью КВЛ и Фарадея можно вычислить напряжения, считываемые вольтметрами в разных положениях, даже если они прикреплены в одних и тех же двух точках кольцо. На этот раз мы включим зонды и увидим, что они вообще не вызывают никаких проблем. Различные значения напряжения — это то, что мы ожидаем измерить, потому что так устроен мир.

Но сначала давайте рассмотрим саму петлю, чтобы увидеть, куда приведет нас «поверхностное» применение закона Фарадея.

Как только мы определили знак тока, который будет течь в кольце (подсказка: он будет следовать \$E_{ind}\$), можно сразу применить закон Фарадея: обходим кольцо по часовой стрелке или против часовой стрелки и вычислить интеграл по пути полного электрического поля. Точно так же мы можем аннотировать все падения напряжения, с которыми мы сталкиваемся на этом пути. С показанным соглашением у нас есть

$$+RH * I + RL * I + …$$

вот и все. больше ничего в петле нет. Мы можем быть уверены в этом, потому что видели общую конфигурацию электрического поля внутри резисторов и проводников. \$E_{tot}\$ (в идеале) равен нулю внутри медных проводников, соединяющих резисторы, поэтому интеграл по путям \$E_{tot}\$ вдоль медных дуг должен быть равен нулю (на самом деле существует крошечная омические потери, вероятно, менее милливольта). У нас осталась правая часть уравнения, которое мы хотим написать. Кирхгоф сказал бы, что она равна нулю, но Фарадей говорит, что она равна минус производная по времени от магнитной индукции B. Или, короче, ЭДС. В эксперименте мы знаем, что поле изменяется таким образом, что возникает ток против часовой стрелки (который следует направлению индуцированного электрического поля \$E_{ind}\$), поэтому наше применение закона Фарадея гласит:

$$ +RH * I + RL * I = ЭДС $$

из которой мы можем вычислить ток I и падение напряжения на резисторах.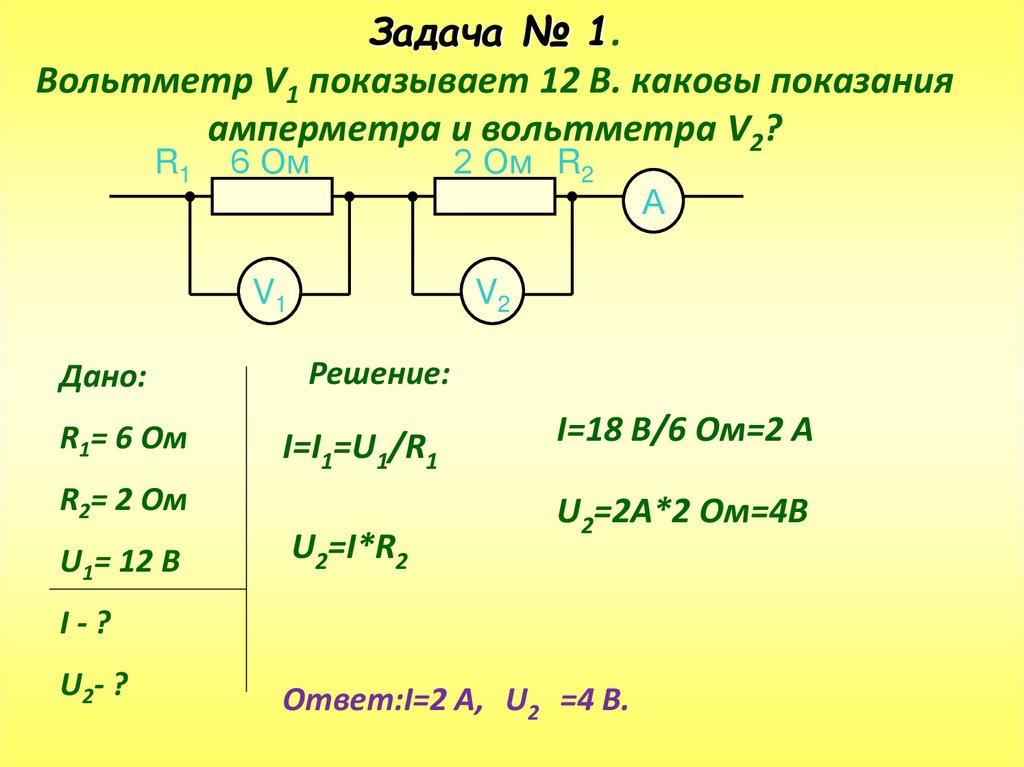 Ток будет 1 мА, и мы получим 0,9 В на RH и 0,1 В через RL (что с положительным стихом, установленным показанной стрелкой, будет означать V2 = -0,1 В) Вас беспокоит тот факт, что вы находите разные значения на резисторах, и, поскольку медь почти ничего не роняет, два разных значения напряжения на двух самых точках А и В? Надеюсь нет. Во-первых, мы знаем, что когда присутствуют переменные магнитные поля, электрическое поле перестает быть консервативным, поэтому мы должны ожидать ненулевых интегралов по путям вдоль замкнутых контуров, а с этим линейных интегралов, зависящих от пути. Во-вторых, мы видели общую конфигурацию электрического поля в кольце, и мы должны были ожидать разные значения интегралов пути, которые идут от A к B вдоль двух разных резисторов. Мы уже знаем, что это никак не связано с наличием (или, в данном случае, отсутствием) зондов.

Теперь давайте добавим эти датчики, чтобы увидеть, как можно применить Фарадея для объяснения различных значений, считываемых вольтметрами с двух сторон кольца.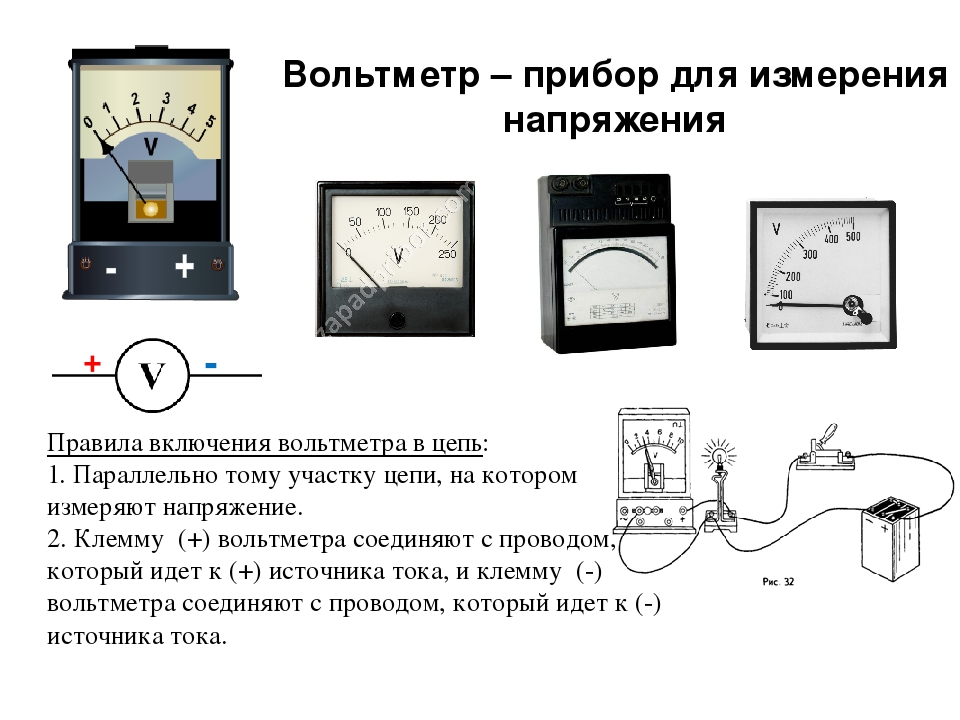 Я нарисую кольцо немного иначе, чтобы подчеркнуть пару моментов:

Обратите внимание, что я намеренно использовал деформированное кольцо и свободно расположенные щупы. Это связано с тем, что, пока область переменного магнитного поля полностью заключена внутри кольца и зонды не прорезают его [примечание], не имеет значения, насколько большим и формой является кольцо. Когда мы анализировали конфигурацию индуцированного электрического поля \$E_{ind}\$, мы видели, что ЭДС, связанная любым путем, полностью охватывающим область dB/dt, всегда одинакова. (В реальном мире, где необходимо учитывать конечную проводимость меди, достаточно большое кольцо будет вносить потери, которые сделают индуцированный ток слишком малым для измерения, но это нас не касается). Единственная разница, которую внесет шаткое кольцо, — это некоторый боковой поверхностный заряд на проводниках, чтобы управлять колумбовым электрическим полем внутри пути. Но полное электрическое поле внутри проводника всегда будет Е = Дж/сигма и направлено по траектории (нулю, в идеальном проводнике) 9. 0009 И еще: по той же причине, что и выше, длина и форма пути зондов не имеют значения. Было бы важно, если бы вы были достаточно неосторожны и позволили значительной части магнитного поля уйти или закрыться в области, где вы размещаете зонды; но это не так в тщательно спланированном эксперименте Левина (хотя я не могу сказать того же об экспериментах, проведенных другими субъектами)

Наконец, обратите внимание, что я использовал другие положительные соглашения для стиха контурных токов. Я сделал это специально, чтобы токи в вольтметрах были положительными, когда показания будут положительными. Схема даст одно и то же решение, как бы я ни решил назвать I2 положительным.

Итак, теперь мы можем применить закон Фарадея к трем петлям. В боковых контурах, содержащих вольтметры, поскольку они не связывают внутри себя какое-либо переменное магнитное поле, закон Фарадея сводится к КВЛ. Однако в среднем цикле KVL умирает, потому что сам цикл содержит область dB/dt. Как и прежде, интеграл по пути полного электрического поля вдоль контура даст вам падение напряжения на двух резисторах и ничего больше. Правая часть уравнения спасает ситуацию, учитывая ЭДС индукции в контуре. Вот уравнения, преобразованные в систему из трех линейно независимых уравнений с тремя неизвестными I1, I2 и Iring.

Решив их и немного помассировав результат, получаем (если я не ошибся!): ЭДС = 1 В) мы получаем

I1 = 89,993 нА
Iring = 1,00008 мА
I2 = -10,007 нА

(обратите внимание, что ток Iring немного превышает 1 мА. Причина в том, что ЭДС немного превышает меньшее сопротивление, чем раньше, потому что RL и RH параллельны внутренним сопротивлениям вольтметра.Также я использую 10 мОм для внутреннего сопротивления вольтметров, когда Левин использовал 100 мОм). Положительное значение I1 и отрицательное значение I2 говорят нам о том, что вольтметр слева покажет положительное напряжение, а вольтметр справа покажет отрицательное значение. Значения напряжений, считываемых каждым вольтметром, соответствуют падениям напряжения на резисторах с их стороны (имеется в виду резистор, входящий в состав контура, для которого можно применить КВЛ), как мы видим:

V1 = Rmeter * I1 = 899,993 мВ
VRH = RH * (Iring – I1) = 899,993 мВ
VRL = RL * (Iring + I2) = 100,007 мВ
V2 = Rmeter * I2 = -100,007 мВ в основном соответствуют значениям, вычисленным только с помощью кольца, с одним проходом закона Фарадея. Единственная ошибка, вносимая пробниками, — это незначительное влияние нагрузки в 7 нВ.

Если вы сдвинете наконечники щупов по кольцу так, чтобы они коснулись диаметрально противоположных точек A и B, вы увидите, что эти уравнения говорят вам о том, что вы будете считывать разные напряжения с помощью вольтметров на противоположных сторонах кольца и не следует искать (несуществующие) перепады напряжения в дугах кольца или щупах. То, что сразу становится ясно, когда вы смотрите на полное электрическое поле в кольце.

В качестве бонуса вот две аппроксимации точного решения

из которых легко увидеть, что токи через вольтметры находятся в том же отношении (не считая ошибки аппроксимации), что и резисторы, следовательно, они находятся в то же соотношение, что и напряжение на резисторах – как и ожидалось.

RH/RL = 900 / 100 = 9
I1/I2 ≈ – 1/(1+0,1)/(1/(1+9) = – 9/1,1 = – 9,091

[ примечание ] Вы можете по-прежнему получают те же измерения, даже если зонды находятся внутри кольца, пока они остаются в стороне от области переменного магнитного поля и не бегают вокруг него. И если вам действительно, действительно нужно поместить зонды внутри области магнитного поля, вы все еще можете использовать Фарадея для вычисления напряжений, считываемых вольтметрами, — вам нужно обратить внимание на геометрию задачи и вычислить, какая часть площади области переменного магнитного поля заключена в какой контур.0003

Voltage – Почему показания вольтметра при нагрузке ниже, чем при питании?

спросил 9 лет, 4 месяца назад

Изменено 2 года назад

Просмотрено 27 тысяч раз

\$\начало группы\$

Из статьи Википедии о последовательных и параллельных схемах:

В качестве примера рассмотрим очень простую схему, состоящую из четырех лампочек и одной батарейки на 6 В. Если провод соединяет батарею с одной лампочкой, со следующей лампочкой, со следующей лампочкой, со следующей лампочкой, а затем обратно с батареей в один непрерывный цикл, лампочки называются последовательными. Если каждая лампочка подключена к батарее отдельной петлей, говорят, что лампочки подключены параллельно. Если четыре лампочки соединены последовательно, через них протекает одинаковый ток, а падение напряжения составляет 1,5 В на каждой лампочке, чего может быть недостаточно для их свечения. Если лампочки соединены параллельно, токи через лампочки объединяются, образуя ток в батарее, в то время как падение напряжения составляет 6,0 В на каждой лампочке , и все они светятся.

Итак, в случае классического примера с резистором, почему, когда вольтметр помещается над резистором, он показывает более низкое напряжение? Разве он не должен показывать то же напряжение, что и питание?

• напряжение
• постоянный ток
• мультиметр
• параллельный

\$\конечная группа\$

4

\$\начало группы\$

В вашем «классическом примере с резисторами» упущена одна вещь — внутреннее сопротивление батареи.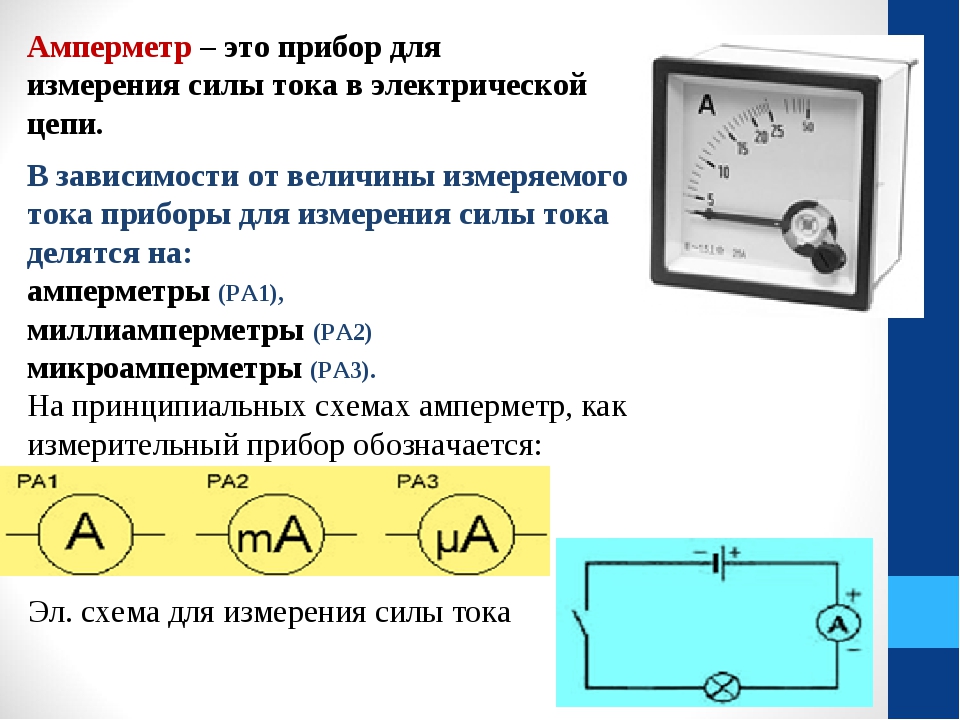

Если вы просто измерите напряжение батареи с помощью вольтметра, вы получите более высокое значение из-за отсутствия (или очень небольшого) падения напряжения на внутреннем сопротивлении батареи.

Напряжение, измеренное на нагрузочном резисторе (или лампочке) ИЛИ на клеммах батареи будет меньше на величину, равную I * R(int).

Соединительный провод имеет очень малое сопротивление и поэтому не способствует значительному падению напряжения между клеммами батареи и резистором, поэтому напряжения в этих двух местах на практике одинаковы.

\$\конечная группа\$

3

\$\начало группы\$

В этих схемах результатом вольтметра является напряжение батареи. Оба 9 В.

^{имитация этой схемы – Схема создана с помощью CircuitLab}

В этой схеме меньше. 3 В.

^{смоделируйте эту схему}

Не путайте две ситуации

\$\конечная группа\$

4

\$\начало группы\$

измерение напряжения питания на источнике питания мы нашли 9В

, но если мы измерим напряжение на нагрузке, мы обнаружим, скажем, 8,03 В, то есть более низкое напряжение, чем напряжение источника.

если представить, что верхний провод имеет сопротивление 6 Ом, а нижний провод имеет сопротивление 6 Ом, то общее сопротивление равно 12 Ом. ) = i(t) X R = 0,0803 x 100 = 8,03 В

падение напряжения в проводе =9-8,3=0,97 В

это из-за сопротивления проводов. Все провода имеют некоторое сопротивление. для уменьшения падения напряжения нужны более толстые провода

\$\конечная группа\$

\$\начало группы\$

Причина, по которой всегда имеет место падение напряжения в электрической цепи без учета внутреннего сопротивления батареи или источника напряжения, заключается в сопротивлении проводов, используемых для соединения цепи.