Что такое динамометр в физике: Динамометр — урок. Физика, 7 класс.

Динамометр | 7 класс | Физика

Содержание

На данном уроке мы познакомимся с новым прибором, с помощью которого можно измерить силу, действующую на тело. Как называют прибор для измерения силы?

Динамометр — это прибор для измерения силы. 

Слово «динамометр» образовано от двух греческих слов: «динамис» — «сила» и «метрео» — «измеряю».

Рассмотрим самый простой вид динамометра — пружинный. Это поможет нам разобраться с принципом действия прибора. Основной его частью является стальная пружина.

Не сложно догадаться, что если подвесить к пружине груз, то она растянется. Другими словами, наблюдатель видит, что на подвешенное тело действует сила, и может определить ее величину.

{"questions":[{"content":"Как называется прибор для измерения силы?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["динамометр","барометр","весы","термометр"],"explanations":["","Это прибор для измерения давления. ","Это прибор для измерения массы.","Это прибор для измерения температуры."],"answer":[0]}}}]}

Устройство пружинного динамометра

Как изготовить простейший динамометр?
Простой пружинный динамометр можно изготовить самостоятельно (рисунок 1). Он состоит из нескольких частей:

• стальная пружина с крючком и указателем на конце;
• корпус для крепления пружины;
• шкала.
Рисунок 1. Основные части динамометра

Сначала закрепляем пружину на корпусе таким образом, чтобы ее нижний конец оставался свободным. Затем к нему прикрепляем указатель. Если разогнуть последний виток пружины, то его можно использовать в качестве указателя.

{"questions":[{"content":"Выберите основные части простейшего пружинного динамометра. [[choice-8]]","widgets":{"choice-8":{"type":"choice","options":["шкала","корпус","пружина с крючком и указателем","подвес","комплект гирь"],"answer":[0,1,2]}}}]}

Градуировка шкалы динамометра

Шкалу можно изготовить из полоски обычной бумаги, нанеся на нее штрихи и числа. Поэтому приклеим бумагу на корпус и сделаем на ней первую отметку (рисунок 2, а). Это будет нулевая отметка, которая показывает, где заканчивается нерастянутая пружина.

Рисунок 2. Градуировка динамометра

Из прошлого урока нам известно, что на груз массой $\frac{1}{9.8} \space кг$ ($102 \space г$) будет действовать сила тяжести, равная $1 \space Н$. Поэтому подвесим на крючок груз указанной массы и посмотрим, насколько растянется пружина.

Если пружина прекратила растяжение и груз остановился, это означает, что сила тяжести, действующая на тело, и сила упругости пружины уравнялись. Новое положение указателя отметим на бумаге, поставив цифру 1 (рисунок 1, б).

Так мы уже получили начало шкалы и необходимо ее продолжить. И сделать это можно по-разному:

1. Поочередно подвешивать грузы массой $204 \space г$, $306 \space г$, $408 \space г$ и т. д., проставляя соответствующие отметки: 2, 3, 4 и т. д.
2. Воспользоваться двумя имеющимися отметками (0 и 1) и с помощью линейки отложить отрезки такой же длины, отметив их числами 2, 3, 4 и т. д.

Теперь у нас есть шкала, которая позволяет измерять силу с точностью до целых. Но точность нашей шкалы можно улучшить до десятых, нанеся на нее дополнительные деления — 0.1; 0.2; 0.3; 0.4 и т. д.

Как нанести на шкалу динамометра деления, соответствующие $0.1 \space Н$?
Для этого разделим расстояние между отметками 0 и 1 на 10 одинаковых частей, поставив соответствующие штрихи. Аналогично поделим на части и другие отрезки ( между отметками 2 и 3, 3 и 4, и т. д.).

Описанным способом мы осуществили градуировку шкалы, цена деления которой равна $0.1 \space Н$. 

{"questions":[{"content":"Если подвесить к динамометру груз, то его пружина растянется до определенной отметки и остановится.  В этот момент силы упругости пружины равна[[choice-14]]","widgets":{"choice-14":{"type":"choice","options":["силе тяжести, действующей на груз","массе груза","времени растяжения пружины до ее остановки","весу пружины"],"answer":[0]}}}]}

Принцип действия динамометра

Итак, мы видим, что для измерения силы, действующей на груз, необходимо уравнять ее с силой растяжения пружины динамометра. Указатель, закрепленный на пружине, покажет величину этой силы согласно шкале. Таким образом, можно сделать вывод, что:

Устройство динамометра основывается на сравнении измеряемой силы с силой упругости пружины.

Например, если подвесить груз какой-то массы, то мы будем сравнивать силу тяжести, действующую на этот груз, и величину силы упругости растянутой пружины.

Если мы возьмем крючок на конце пружины и потянем за него, то мы будем сравнивать силу, приложенную нами, с силой упругости пружины (рисунок 3). Так, с помощью динамометра можно измерять различные силы.

Рисунок 3. Измерение с помощью динамометра приложенной силы

Вспомним закон Гука — он гласит, что сила упругости тела при растяжении прямо пропорциональна изменению длины тела. Принцип работы динамометра подтверждает этот закон — пружина удлиняется во столько же раз, во сколько увеличивается сила ее упругости.

{"questions":[{"content":"Принцип действия динамометра основан на сравнении приложенной к нему силы с[[choice-18]]","widgets":{"choice-18":{"type":"choice","options":["силой упругости пружины","весом пружины","удлинением пружины","силой тяжести, действующей на пружину"],"answer":[0]}}}]}

Виды динамометров

Какие типы динамометров вам известны?
Можно выделить несколько видов динамометров на основе принципа их действия:

1. Механические динамометры (рычажные или пружинные) 

В основе работы механических динамометров лежит деформация. Принцип действия пружинного динамометра подробно описан выше. В рычажном динамометре под действием измеряемой силы происходит деформация рычага, которая и показывает величину силы.

2. Гидравлические динамометры 

Принцип действия таких динамометров основан на определении количества жидкости, вытесняемой из цилиндра под действием измеряемой силы.

3. Электрические динамометры

У таких динамометров имеется датчик, который преобразует деформацию в электрический сигнал. Это вид динамометров стал широко применяться в последнее время.

Современные модели динамометров могу соединять и использовать в себе несколько принципов действия.

{"questions":[{"content":"Определите вид динамометра по его описанию. [[matcher-1]]","widgets":{"matcher-1":{"type":"matcher","labels":["Механические динамометры","Гидравлические динамометры","Электрические динамометры"],"items":["Динамометры, в основе работы которых лежит деформация","Динамометры, принцип действия которых основан на определении количества жидкости, вытесняемой из цилиндра под действием измеряемой силы","Динамометры, которые имеют датчик, который преобразует деформацию в электрический сигнал"]}}}]}

Применение динамометров

Динамометры имеют очень широкое применение. Например, в медицине используются специальные медицинские динамометры. Они предназначены для измерения силы различных мышечных групп человека.

Одним из таких приборов является ручной динамометр, который называется силомером (рисунок 4). С его помощью измеряется мускульная сила руки при сжатии кисти в кулак.

Рисунок 4. Силомер — электронный кистевой динамометр

Для того чтобы измерить тяговые усилия локомотивов, тракторов, морских буксиров и другой техники, используют специальные тяговые динамометры (рисунок 5).

Рисунок 5. Применение тягового динамометра

Такие динамометры способны измерять силы до нескольких десятков тысяч ньютонов. Современные модели имеют пульт дистанционного управления с дисплеем (рисунок 6).

Рисунок 6. Тяговый динамометр

При монтаже проводов и кабелей используют динамометры для определения силы натяжения провода (рисунок 7). Существуют специальные монтажные таблицы с необходимыми значениями. 

Рисунок 7. Динамометр для монтажных работ

Динамометры используют не только в специальной технике, но и в обычных для нас местах: в метро, в автобусах и даже в лифте. Здесь эти приборы используют для измерения силы сжатия створок различных автоматических дверей.

{"questions":[{"content":"Динамометр, с помощью которого можно измерить мускульную силу руки, называется[[choice-22]]","widgets":{"choice-22":{"type":"choice","options":["силомером","монтажным","тяговым","гидравлическим"],"answer":[0]}}}]}

Упражнения

Упражнение №1

Определите цену деления каждого прибора и силу тяжести, действующую на каждый груз (рисунок 8).

Рисунок 8. Динамометры с грузами

Показать ответ

Скрыть

Определим цену деления динамометра, изображенного на рисунке 8, а. Возьмем два крайних подписанных деления: $1 \space Н$ и $0 \space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$\frac{1 \space Н \space − \space 0 \space Н}{10} = 0.1 \space Н$.
Цена деления этого динамометра равна $0.1 \space Н$.
На подвешенный груз действует сила тяжести, равная $1 \space Н$.

Определим цену деления динамометра, изображенного на рисунке 8, б. Возьмем два крайних подписанных деления: $1 \space Н$ и $0 \space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$\frac{1 \space Н \space − \space 0 \space Н}{2} = 0.5 \space Н$.
Цена деления этого динамометра равна $0.5 \space Н$.
На подвешенный груз действует сила тяжести, равная $6 \space Н$.

Упражнение №2

Чему равен вес каждого груза на рисунке 8? Укажите точку его приложения.

Показать ответ

Скрыть

Груза и динамометры у нас неподвижны, поэтому вес каждого груза будет равен силе тяжести, действующей на него. Значение же силы тяжести мы видим по показаниям динамометров.

Для груза на рисунке 8, а:
$P = F_{тяж} = 1 \space Н$.

Для груза на рисунке 8, б:
$P = F_{тяж} = 6 \space Н$.

На рисунке 9 изображен вес этих тел.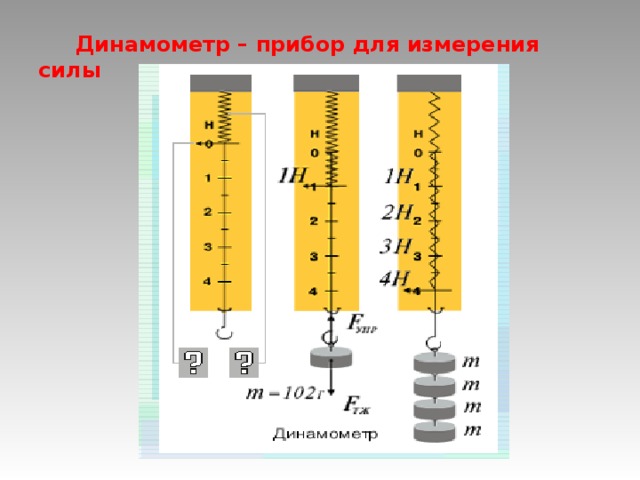 Вес приложен к подвесу в обоих случаях.

Рисунок 9. Вес подвешенных грузов

Упражнение №3

По рисунку 10 определите, с какой силой растягивается каждая пружина под действием подвешенного к ней груза (масса одного груза $102 \space г$).

Рисунок 10. Растяжение пружины под действием груза

Дано:
$m = 102 \space г$
$g = 10 \frac{Н}{кг}$

СИ:
$m = 0.102 \space кг$

$F_1 — ?$
$F_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Под действием какой силы будет растягиваться пружина? Она растягивается под влиянием силы тяжести, действующей на подвешенный к ней груз.

Рассчитаем силу, растягивающую причину на рисунке 10, а:
$F_1 = F_{тяж1} = gm$,
$F_1 = 10 \frac{Н}{кг} \cdot 0.102 \space кг = 1.02 \space Н$.

Рассчитаем силу, растягивающую причину на рисунке 10, б:
$F_2 = F_{тяж2} = g \cdot 2m$,
$F_2 = 10 \frac{Н}{кг} \cdot 2 \cdot 0.102 \space кг = 2.04 \space Н$.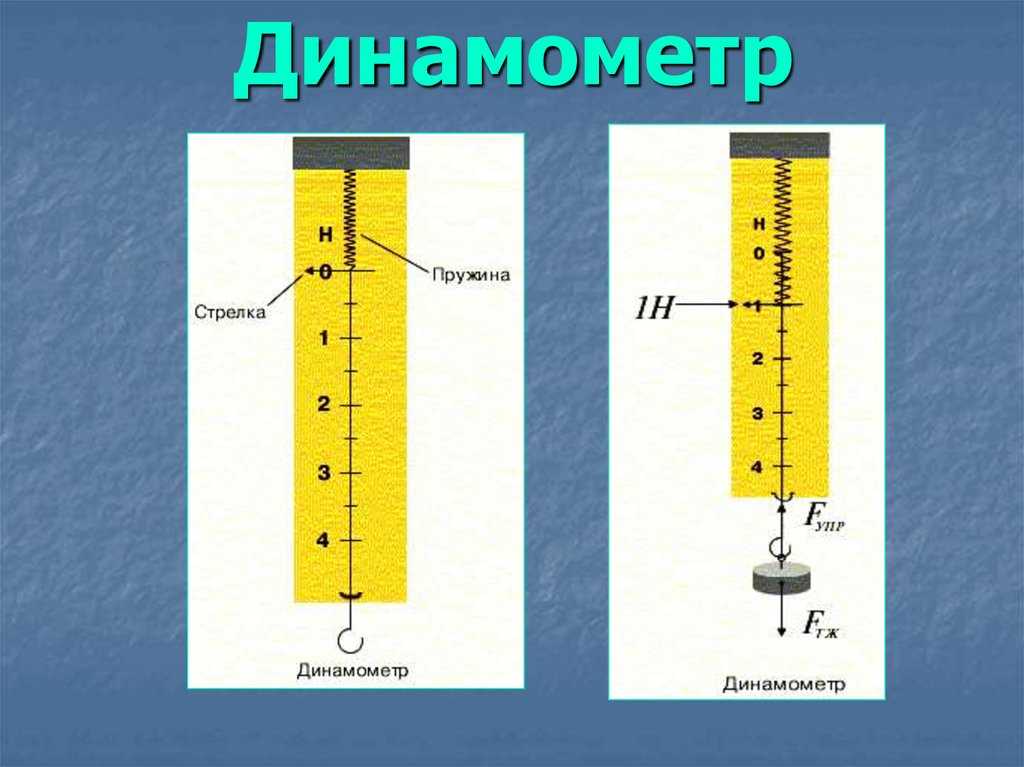

Ответ: $F_1 = 1.02 \space Н$, $F_2 = 2.04 \space Н$.

Динамометр – шкала измерения, принцип действия прибора и физическая величина (7 класс)

4.6

Средняя оценка: 4.6

Всего получено оценок: 77.

Обновлено 4 Марта, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 77.

Обновлено 4 Марта, 2021

Из курса физики в 7 классе известно, что для измерения физических величин существует ряд специальных приборов — начиная от простейшей измерительной линейки и заканчивая сложными устройствами в ядерной физике. Поскольку механика — это наука о силах, важнейшим измерительным прибором здесь является динамометр, измеряющий силу. Принцип действия динамометра напрямую связан с его устройством: наличием упругого элемента и измерительной системы.

Сила и ее измерение

Сила в механике — это мера взаимодействия тел. Сила выражает степень механического действия одного тела на другое, и именно сила является причиной изменений движения (ускорения) тел.

Вне действия сил любое тело либо находится в покое, либо движется прямолинейно и равномерно.

Как и большинство физических характеристик, силы имеют величину, что позволяет их сравнивать между собой. И, поскольку действие силы выражается в сообщении телу ускорения, то единица измерения силы базируется на этом свойстве.

Единицей измерения силы в СИ принята такая сила, которая сообщает массе 1 килограмм ускорение 1 метр в секунду за секунду. Эта единица называется «ньютон».

Рис. 1. Сила в физике.

Динамометр

Прибор, предназначенный для измерения силы, называется динамометр.

Однако измерять силу, исходя из ускорения, которое эта сила оказывает на тело известной массы, неудобно в практическом плане. Измеряемая сила должна действовать на какое-то тело внутри прибора, сообщая ему ускорение, — конструкция получается сложной.

Более серьезная проблема состоит в том, что измерительный прибор должен вносить минимальные искажения в измеряемую систему, а если направить измеряемую силу на создание ускорения, то работа силы будет переключена на этот процесс, что существенно повлияет на измеряемую механическую систему, в которую эта работа уже не поступит.

Поэтому для измерения силы необходимо использовать другое физическое явление — сравнение с силой упругости. Такой подход значительно упрощает измерение.

Во-первых, сила упругости может быть легко «передана» другому предмету, что позволяет «встраивать» динамометр в механическую систему. При этом измеряемая сила будет прилагаться к динамометру, а через его упругий элемент — передаваться дальше в механической системе. Искажения получаются минимальны, вся работа силы остается в системе.

Во-вторых, сила упругости большинства упругих веществ линейна в достаточно широком диапазоне. Следовательно шкала измерения динамометра получается линейной, что упрощает использование прибора.

Таким образом, динамометр должен состоять из упругого элемента и индикаторной системы, позволяющей видеть степень его изгиба. В простейшем случае упругим элементом служит обычная пружина, а индикаторной системой — обычная линейка. В более сложных устройствах упругим элементом могут быть рессоры, гидравлические и газонаполненные емкости, специальные тензодатчики.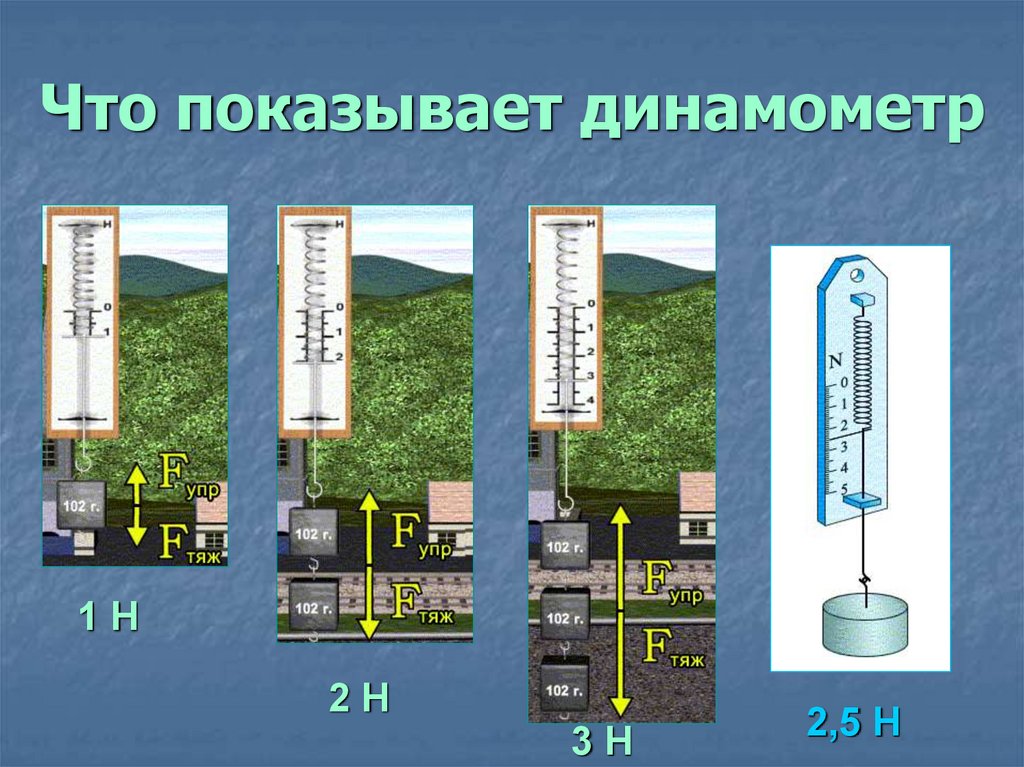 Индикаторная система может преобразовывать изгиб в движение стрелки, поворот барабана с цифрами или в цифровое представление на алфавитно-цифровом дисплее.

Рис. 2. Устройство динамометра.

В обиходе часто используются пружинные весы. По сути, такие весы являются динамометром. Хотя их шкала размечена в единицах массы, на самом деле они измеряют силу тяжести, действующую на взвешиваемое тело, оценивая изгиб пружины. Поскольку сила тяжести прямо пропорциональна массе, шкала весов получается линейной. Внимательно рассмотрев пружинные весы, можно понять, что они отличаются от динамометра только шкалой.

Рис. 3. Пружинные весы.

Что мы узнали?

Динамометр — прибор для измерения силы. Динамометр состоит из упругого элемента и измерительной системы. В простейшем случае упругий элемент — это пружина, а измерительная система — это линейка. При измерении силы упругий элемент изгибается, изгиб измеряется по шкале, проградуированной в единицах силы — в ньютонах.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 77.

---

А какая ваша оценка?

Динамометр $D$ прикреплен к двум телам массой $M = 6кг$ и к ним приложена сила $f = 20Н$. Какими будут показания динамометра?

Ответить

Проверено

231,6 тыс.+ просмотров

Подсказка: Динамометр — это устройство, которое используется для измерения силы. В этом вопросе нам нужно определить показание динамометра таким образом, чтобы прикладывалась сила с обоих концов масс, прикрепленных к динамометру. Для этого воспользуемся законом движения Ньютона и теорией диаграмм свободного тела.

Полный пошаговый ответ:
Рассмотрим динамометр, как показано на рисунке ниже, соединенный с двумя массами $M = 6 кг$ каждая, и к массам приложена сила $20Н$.





Усредненная сила задается как:
$
{F_{avg}} = \dfrac{{20 + 20}}{2} \\
= \dfrac{{40}}{2} \\
= 20N \\
 $
Пусть показание динамометра равно x ньютонов.
Теперь, поскольку и массы, и силы равны и действуют в противоположных направлениях, чистое показание динамометра связано с обоими, так что два тела производят одинаковое и противоположное ускорение из-за результирующей силы.
Теперь, следуя закону Ньютона: Сила$ = $mass$ \times $acceleration
Для первого блока результирующая сила$ = \left( {20 – x} \right)N$ в правильном направлении и масса$ = 6 кг $
Итак, ускорение$ = \dfrac{{\left( {20 – x} \right)}}{6}$
Аналогично, для второго тела
Acceleration$ = \dfrac{{\left( {20 – x} \right)}}{6}$
Так как оба ускорения равны, то значение $x$ будет равно половине всех сил, так как силы также равны, поэтому $x = F = 20N$
Следовательно, динамометр показывает $20N$ в установившемся режиме.

Примечание: Динамометр считывает значение между заданной силой и нижней силой. Здесь заданная сила$ = 20 Н$ и нижняя сила$ = 20 Н$.
Значит, это $20N$.
Но в случае разных сил и масс показания будут другими.


Недавно обновленные страницы

Какой элемент обладает наибольшим атомным радиусом А класс 11 химия JEE_Main

Высокоэффективный метод получения бериллия 11 класс химия JEE_Main

Какой из следующих сульфатов имеет наибольшую растворимость 11 класса химии JEE_Main

Среди металлов Be Mg Ca и Sr группы 2 11 класса химии JEE_Main

Какой из следующих металлов присутствует в зеленом цвете 11 класса химии JEE_Main

Для предотвращения окисления магния в электролите 11 класс химии JEE_Main

Какой элемент обладает наибольшим атомным радиусом А 11 класс химии JEE_Main

Высокоэффективный метод получения бериллия 11 класс химии JEE_Main

Какой из следующих сульфатов имеет наибольшую растворимость 11 класса JEE_Main

Среди металлов Be Mg Ca и Sr группы 2 11 класса JEE_Main

Какой из следующих металлов присутствует в зеленом цвете 11 класса JEE_Main

Для предотвращения окисления магния в электролитах класса 11 химии JEE_Main

Тенденции сомнения

Измерение изометрического пикового крутящего момента и скорости развития крутящего момента в режиме реального времени с использованием нового устройства для испытания прочности: исследование достоверности и надежности

. 2020 9 декабря; 41 (11).

doi: 10.1088/1361-6579/abc40b.

Тай Б Палмер ¹ , Джаррод Блинч ¹ , Ахали С Фэрроу ¹ , Чинонье С Агу-Удемба ¹ , Итан А Митчелл ¹

принадлежность

• ¹ Кафедра кинезиологии и спортивного менеджмента, Техасский технический университет, Лаббок, Техас, Соединенные Штаты Америки.
• PMID: 33091881
• DOI: 10.1088/1361-6579/abc40b

Ty B Palmer et al. Физиол Изм. 2020 .

. 2020 9 декабря; 41 (11).

doi: 10.1088/1361-6579/abc40b.

Авторы

Тай Б Палмер ¹ , Джаррод Блинч ¹ , Ахали С Фэрроу ¹ , Чинонье С Агу-Удемба ¹ , Итан А Митчелл ¹

принадлежность

• ¹ Кафедра кинезиологии и спортивного менеджмента, Техасский технический университет, Лаббок, Техас, Соединенные Штаты Америки.
• PMID: 33091881
• DOI: 10. 1088/1361-6579/abc40b

Абстрактный

Цель : Изометрический пиковый крутящий момент (PT) и скорость развития крутящего момента (RTD) являются важными характеристиками, относящимися к спортивным результатам. Новое устройство под названием Dynamo Torque Analyzer вычисляет и отображает измерения изометрического PT и RTD в режиме реального времени. Однако способность Dynamo обеспечивать достоверные и надежные изометрические измерения PT и RTD, подобные измерениям изокинетического динамометра, остается неясной. Это исследование было направлено на сравнение надежности и величины измерений PT и RTD изометрического разгибания и сгибания ног с помощью изокинетического динамометра и анализатора крутящего момента Dynamo.

Подход . Двадцать здоровых, рекреационно-активных взрослых (возраст = 22 ± 3 года, рост = 169 ± 10 см, масса = 71 ± 18 кг) выполнили три изометрических разгибания и сгибания ног с максимальным произвольным сокращением в двух разных случаях, из которых Изометрический PT и ранние (RTD100), поздние (RTD200) и максимальные (Peak RTD) характеристики RTD измеряли с помощью изокинетического динамометра и Dynamo. Основные результаты : Характеристики PT и RTD при изометрическом разгибании и сгибании ноги были в высокой степени стабильными между сеансами как для изокинетического динамометра, так и для устройств Dynamo, с внутриклассовыми коэффициентами корреляции 0,9.35-0,984 и стандартные ошибки измерения, выраженные в процентах от среднего значения 4,93-14,46%. Между данными изокинетического динамометра и Dynamo для всех характеристик PT и RTD наблюдалась значительная положительная взаимосвязь ( r ≥ 0,994; P <0,001). При этом существенных различий между устройствами по этим переменным не наблюдалось ( P = 0,107-0,555). Значение : Эти данные свидетельствуют о том, что анализатор крутящего момента Dynamo может быть действительным и надежным устройством для измерения изометрического PT и RTD мускулатуры нижней части тела.

Ключевые слова: последовательность; сокращение; изокинетический динамометр; портативный; преобразователь.

© 2020 Физико-технический институт медицины.

Похожие статьи

• Полезность характеристик пикового крутящего момента и скорости развития крутящего момента для определения способности к ходьбе у пожилых женщин.

  Палмер Т.Б., Блинч Дж., Фэрроу А.С., Агу-Удемба К.С., Митчелл Э.А. Палмер Т.Б. и соавт. J Musculoskelet Нейрональное взаимодействие. 2021 1 декабря; 21 (4): 455-463. J Musculoskelet Нейрональное взаимодействие. 2021. PMID: 34854384 Бесплатная статья ЧВК.

• Пиковый крутящий момент объясняет более уникальную изменчивость показателей роста, чем скорость развития крутящего момента у мальчиков и девочек.

  Gillen ZM, Shoemaker ME, McKay BD, Bohannon NA, Gibson SM, Cramer JT. Гиллен З.М. и соавт. J Прочность Конд Рез. 2020 сен;34(9)):2507-2514. doi: 10.1519/JSC.0000000000003728. J Прочность Конд Рез. 2020. PMID: 32639374

• ДЕЙСТВИТЕЛЬНОСТЬ РУЧНОЙ ДИНАМОМЕТРИИ ДЛЯ ИЗМЕРЕНИЯ СИЛА КВАДРИЦЕПСА И СКОРОСТИ РАЗВИТИЯ МОМЕНТА.

  Леснак Дж., Андерсон Д., Фармер Б., Кацавелис Д., Гриндстафф Т.Л. Леснак Дж. и соавт. Int J Sports Phys Ther. 2019 апр;14(2):180-187. Int J Sports Phys Ther. 2019. PMID: 30997270 Бесплатная статья ЧВК.

• Оптимизация межсессионной надежности показателей пикового крутящего момента четырехглавой мышцы и скорости развития крутящего момента.

  Гриндстафф Т.Л., Палименио М.Р., Франко М., Андерсон Д., Бэгвелл Дж.Дж., Кацавелис Д. Гриндстафф Т.Л. и др. J Прочность Конд Рез. 2019 июль;33(7):1840-1847. doi: 10.1519/JSC.0000000000002821. J Прочность Конд Рез. 2019. PMID: 30289874

• Влияние спортивного статуса на характеристики максимального и быстрого изометрического крутящего момента и показатели постурального баланса у спортсменок Дивизиона I и контрольной группы, не занимающихся спортом.

  Палмер Т.Б., Хоки М.Дж., Тиле Р.М., Кончола Е.К., Адамс Б.М., Акехи К., Смит Д.Б., Томпсон Б.Дж. Палмер Т.Б. и соавт. Clin Physiol Funct Imaging. 2015 июль;35(4):314-22. doi: 10.1111/cpf.12167. Epub 2014 29 мая. Clin Physiol Funct Imaging. 2015. PMID: 248

Посмотреть все похожие статьи

Цитируется

• Скорость развития крутящего момента как дискриминатор уровня игры у университетских футболисток.

  Палмер Т.Б., Акехи К. Палмер Т.Б. и соавт. J Musculoskelet Нейрональное взаимодействие. 2022 1 сентября; 22 (3): 326-335. J Musculoskelet Нейрональное взаимодействие. 2022. PMID: 36046988 Бесплатная статья ЧВК.

• Влияние комплексной противоотечной терапии на боль и функциональные возможности у лиц с раком молочной железы, у которых развился адгезивный капсулит из-за лимфедемы: оценка с помощью изокинетической компьютеризированной системы.

  Татарский К.К., Турхан Б. Татарский К.К. и др. Корейский Джей Пейн. 2022 1 июля; 35 (3): 280-290. doi: 10.3344/kjp.2022.35.3.280. Корейский Джей Пейн. 2022. PMID: 35768983 Бесплатная статья ЧВК.

• Полезность характеристик пикового крутящего момента и скорости развития крутящего момента для определения способности к ходьбе у пожилых женщин.