Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Навигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник – формулы – длина стороны – радиус вписанной окружности – радиус описанной окружности – площадь – периметр – угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
 1 |
Рис.2 |
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
2. Все углы равны:
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:180° · (n – 2)
5. Сумма всех внешних углов n-угольника равна 360°:β 1 + β2 + β3 + .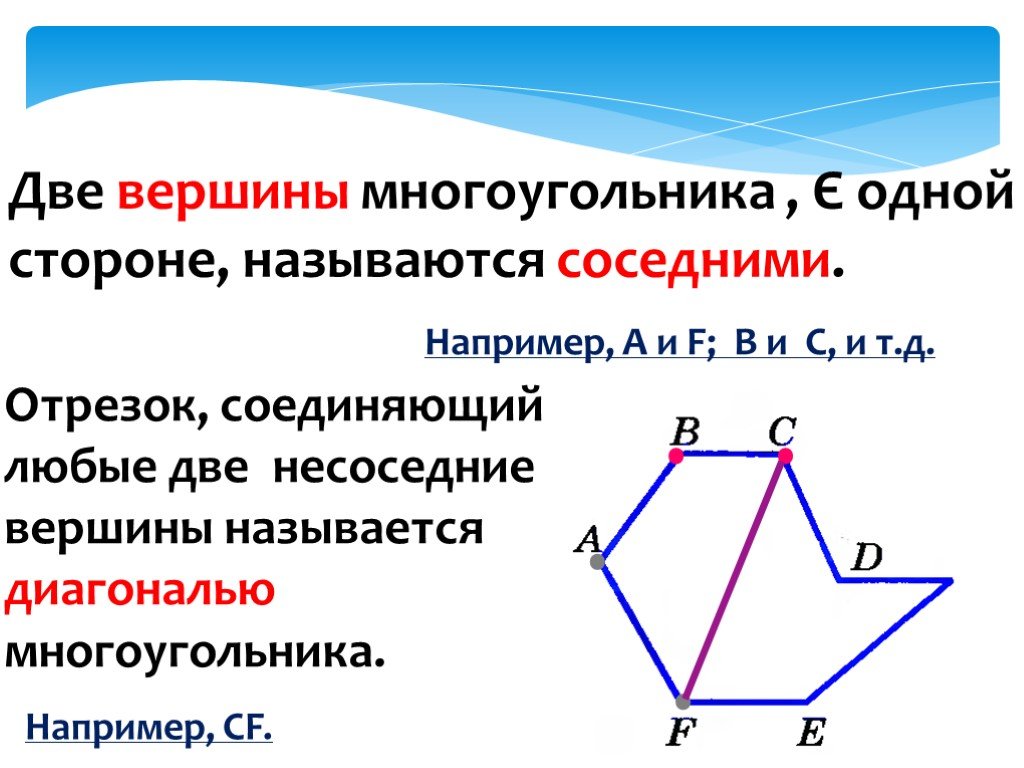
.. + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
| Dn = | n · (n – 3) |
| 2 |
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
| S = | π | a2 |
| 4 |
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник – формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
| a = 2r · tg | 180° |
| n |
| a = 2r · tg | π |
| n |
2.
Формула стороны правильного n-угольника через радиус описанной окружности:
| a = 2 R · sin | 180° |
| n |
| a = 2 R · sin | π |
| n |
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
| r = a : (2tg | 180° | ) |
| n |
| r = a : (2tg | π | ) |
| n |
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
| R = a : (2sin | 180° | ) |
| n |
| R = a : (2sin | π | ) |
| n |
Формулы площади правильного n-угольника
1.
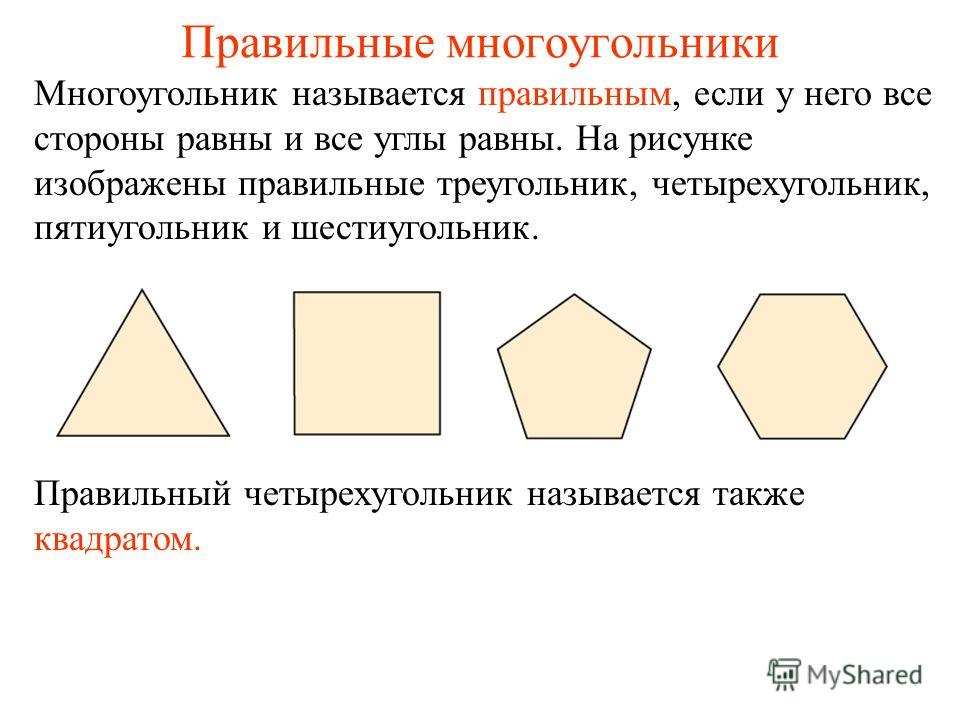Формула площади n-угольника через длину стороны:
| S = | na2 | · ctg | 180° |
| 4 | n |
2. Формула площади n-угольника через радиус вписанной окружности:
| S = | nr2 · tg | 180° |
| n |
3. Формула площади n-угольника через радиус описанной окружности:
| S = | nR2 | · sin | 360° |
| 2 | n |
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
| n – 2 | · 180° | |
| n |
Рис. 3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
| r = | a√3 |
| 6 |
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
| R = | a√3 |
| 3 |
5. Формула площади правильного треугольника через длину стороны:
| S = | a2√3 |
| 4 |
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 4 |
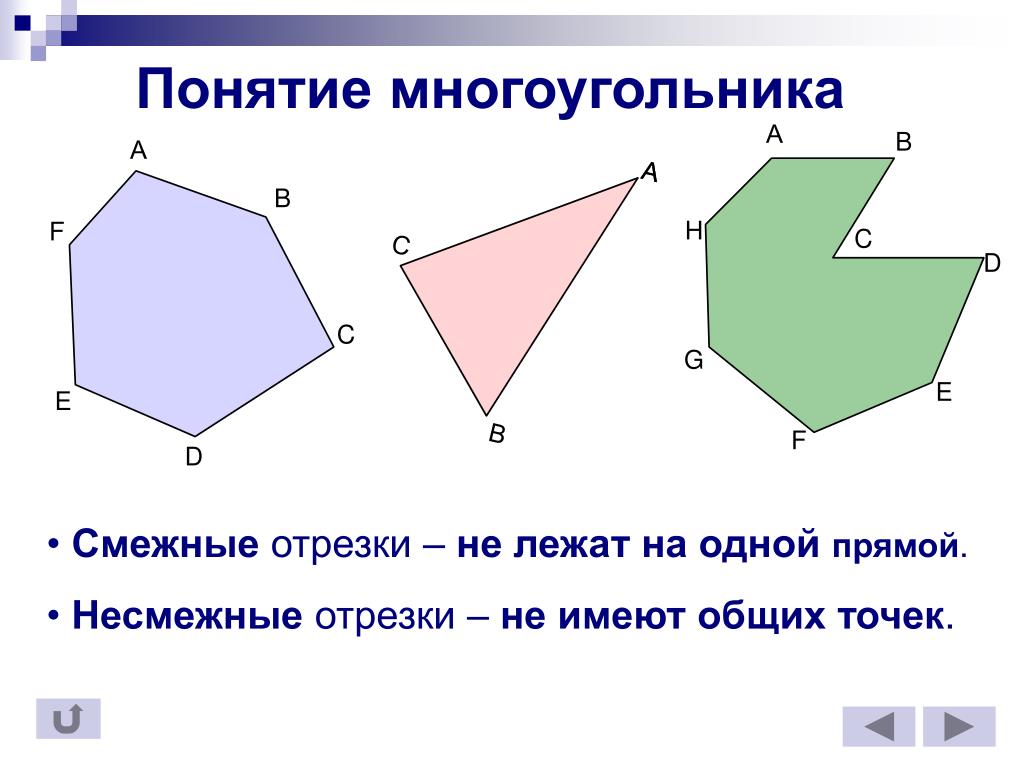Угол между сторонами правильного треугольника:α = 60°
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику – квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
| r = | a |
| 2 |
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
| R = | a√2 |
| 2 |
S = a2
6.
Формула площади правильного четырехугольника через радиус вписанной окружности:S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:S = 2 R2
8. Угол между сторонами правильного четырехугольника:α = 90°
Смотрите также формулы и свойства квадрата
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
| a = | 2√3 | r |
| 3 |
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
| r = | a√3 |
| 2 |
R = a
5.
Формула площади правильного шестиугольника через длину стороны:
| S = | a2 3√3 |
| 2 |
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 2 |
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:a = 2r · (√2 – 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:a = R√2 – √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
| r = | a(√2 + 1) |
| 2 |
4.
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
| R = | a√4 + 2√2 |
| 2 |
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:S = r2 8(√2 – 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:α = 135°
Все таблицы и формулы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике – Планиметрия
Поиск по сайту:| Формулы для стороны, периметра и площади правильного n – угольника |
| Формулы для стороны, периметра и площади правильного треугольника |
| Формулы для стороны, периметра и площади правильного шестиугольника |
| Формулы для стороны, периметра и площади квадрата |
Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.
Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.
Замечание 1. В любой правильный многоугольник можно вписать окружность.
Замечание 2. Около любого правильного многоугольника можно описать окружность.
Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Используемые обозначения
| Число вершин правильного многоугольника | Сторона правильного многоугольника | Радиус вписанной окружности | Радиус описанной окружности | Периметр | Площадь |
| n | a | r | R | P | S |
| Число вершин правильного многоугольника | n |
| Сторона правильного многоугольника | a |
| Радиус вписанной окружности | r |
| Радиус описанной окружности | R |
| Периметр | P |
| Площадь | S |
Формулы для стороны, периметра и площади правильного
n – угольника| Величина | Рисунок | Формула | Описание |
| Периметр | P = an | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Площадь | Выражение площади через сторону | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного n – угольника |
Выражение периметра через сторону P = an Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного n – угольника |
Выражение площади через сторону и радиус вписанной окружности Выражение площади через сторону Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного n – угольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного треугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 3a | Выражение периметра через сторону | |
| Площадь | Посмотреть вывод формулы | Выражение площади через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного треугольника |
Выражение периметра через сторону P = 3a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного треугольника |
Выражение площади через сторону Посмотреть вывод формулы Выражение площади через сторону и радиус вписанной окружности Выражение площади через радиус вписанной окружности Посмотреть вывод формулы Выражение площади через радиус описанной окружности Посмотреть вывод формулы |
| Формулы для стороны правильного треугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного шестиугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 6a | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону | ||
| Площадь | S = 3ar | Выражение площади через сторону и радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | a = R | Выражение стороны через радиус описанной окружности | |
| Периметр | P = 6R | Выражение периметра через радиус описанной окружности | |
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного шестиугольника |
Выражение периметра через сторону P = 6a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности P = 6R |
| Формулы для площади правильного шестиугольника |
Выражение площади через сторон Выражение площади через сторону и радиус вписанной окружности S = 3ar Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного шестиугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности a = R |
Формулы для стороны, периметра и площади квадрата
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 4a | Выражение периметра через сторону | |
| Площадь | S = a2 | Выражение площади через сторону | |
| Сторона | a = 2r | Выражение стороны через радиус вписанной окружности | |
| Периметр | P = 8r | Выражение периметра через радиус вписанной окружности | |
| Площадь | S = 4r2 | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | S = 2R2 | Выражение площади через радиус описанной окружности |
| Формулы для периметра квадрата |
Выражение периметра через сторону P = 4a Выражение периметра через радиус вписанной окружности P = 8r Выражение периметра через радиус описанной окружности |
| Формулы для площади квадрата |
Выражение площади через сторону S = a2 Выражение площади через радиус вписанной окружности S = 4r2 Выражение площади через радиус описанной окружности S = 2R2 |
| Формулы для стороны квадрата |
Выражение стороны через радиус вписанной окружности a = 2r Выражение стороны через радиус описанной окружности |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Home – N Square
Шестая группа стипендиатов-инноваторов N Square представила, как может выглядеть мир в 2095 году без ядерного оружия.
Операционная система 22 века
Два лидера Движения черных спекулятивных искусств рассказывают о своем новом сотрудничестве с N Square и о том, что афрофутуризм привносит в задачу создания будущего, свободного от ядерной угрозы.
В Афробудущее
Новая группа стипендиатов NSIN разрабатывает прорывные решения для ряда проблем в масштабах всей области.
Внутренние инновации
У аналитика по финансовым исследованиям и сотрудника N Square Дэвида Эпштейна есть сообщение для устойчивых инвесторов: риск, о котором они не говорят, может быть самым большим из всех.
Пришло время привлечь инвесторов
По словам режиссера Райана Бейкерта, единственный способ активизировать общественное участие в ядерной проблематике — раскрыть силу истории.
Режиссер в командировке
Пандемия выдвигает на первый план новую и неотложную возможность отточить важные навыки управления неопределенностью и прогнозирования будущего.
Адаптация к сбоям
Эмма Белчер из Фонда Макартуров перешла от изучения политики в области ядерных вооружений к поддержке новаторских идей по ее улучшению — и она хочет, чтобы другие спонсоры присоединились к ее поискам.
Ученый
Новое шоу, задуманное ребятами из N Square, предлагает хмельной взгляд на отрезвляющие ядерные угрозы.
Дебют бомбы
Специалисты по ядерной угрозе переосмысливают свою область деятельности
Мы расширяем свое присутствие в округе Колумбия, привнося сотрудничество и совместное обучение в самое сердце сообщества ядерного нераспространения.
Запуск центра постоянного тока N Square
В 2017 году ICAN получила Нобелевскую премию за работу по заключению глобального договора о запрещении ядерного оружия. Но исполнительный директор Беатрис Фин нацелилась на большую награду — сделать ядерное оружие невозможным.
Нобелевская премия мира. Что теперь?
Познакомьтесь с стипендиатами N Square — активной межотраслевой группой технологов, дизайнеров игр, экспертов по политике, дипломатов, голливудских режиссеров и многих других, которые вместе решают ядерные проблемы новыми способами.
N Square Fellows
Иконоборец, движимый большими идеями, обращает свой взор на ядерные угрозы.
Ричард Брэнсон становится ядерным
В области ядерной безопасности самые доминирующие голоса не следует путать с самыми законными.
Ответственное нарушение
Директор по политике и глобальной безопасности Фонда Сколл выступает за новый филантропический подход к поддержке инноваций в ядерной области.
Дипломат
Мишель Довер из фондаPlowshares Fund рассказывает о роли гражданского общества и неожиданных новых голосах в снижении ядерной угрозы.
Переговорщик
Новое партнерство между экспертами в области политики, разработчиками игр и общественным радио приводит к созданию симуляции с высокими ставками, которая позволяет пользователям решать: ядерная атака или ложная тревога?
Пять минут на спасение мира
Как One Earth Future Foundation и его лидер Future Labs Джон Беллиш делают ставку на сетевую координацию и открытые данные как на ключи к предотвращению ядерной войны.
Инкубационный мир
Первопроходец, финансирующий мир и безопасность, Карл Робишо рассказывает о рисках и преимуществах поиска (и финансирования) новых способов борьбы с экзистенциальными угрозами.
Рискованный
Первая из серии историй о том, что может случиться, когда странные партнеры объединят свои усилия, чтобы зажечь ядерные инновации.
Лейси Хили и вещи, которые идут бум
Как исследователи из Принстонской лаборатории ядерного будущего привносят полномасштабную виртуальную реальность в работу по разоружению.
Проверка становится виртуальной
Как ученый, создавший вирусный хит NUKEMAP, планирует заново изобрести Гражданскую оборону.
Невероятный историк
Аналитик-ядерщик Мелисса Хэнхем рассказывает о ядерном арсенале Северной Кореи, о том, как она отслеживает его деятельность по распространению, и почему общественная проверка — это путь будущего.
Сыщик с открытым исходным кодом
Чтобы понять будущее инноваций в области ядерной угрозы, полезно заглянуть в прошлое и настоящее.
Навигация по временной шкале инноваций
Репетиторство по математике для экспертов в Великобритании
Сумма квадратов n натуральных чисел может быть рассчитана по формуле [n(n+1)(2n+1)] / 6. Пусть n — натуральное число. Мы оцениваем сумму квадратов в статистике, чтобы найти изменение данных. Существуют различные методы нахождения суммы квадратов заданных чисел.
В этой статье мы обсудим формулу для вычисления суммы квадратов n натуральных чисел и докажем ее, используя принцип математической индукции. Мы также обсудим формулу для нахождения суммы квадратов четных и нечетных натуральных чисел и суммы квадратов в геометрии. Мы также решим несколько примеров для лучшего понимания концепции.
| 1. | Что такое сумма квадратов n натуральных чисел? |
| 2. | Формула суммы квадратов n натуральных чисел |
| 3. | Сумма квадратов двух и трех чисел |
4. | Сумма квадратов натуральных чисел Доказательство |
| 5. | Сумма квадратов четных натуральных чисел |
| 6. | Сумма квадратов нечетных натуральных чисел |
| 7. | Сумма квадратов в геометрии |
| 8. | Часто задаваемые вопросы о сумме квадратов |
Что такое сумма квадратов n натуральных чисел?
Давайте сначала вспомним значение натуральных чисел. Натуральные числа — это числа, которые считаются от 1 до бесконечности. Если рассматривать n последовательных натуральных чисел, то нахождение суммы квадратов этих чисел представляется как Σ i = 1 n i 2 . Мы можем найти сумму квадратов первых n натуральных чисел , используя формулу СУММ = 1 2 + 2 2 + 3 2 + … + n 2 = [n(n+1)(2n+1)] / 6. Мы можем доказать эту формулу, используя принцип математической индукции.
☛ Также проверьте: Сумма квадратов
Давайте пройдемся по формулам нахождения суммы квадратов четных и нечетных натуральных чисел в следующем разделе.
Сумма квадратов n натуральных чисел Формула
Вот формулы для нахождения суммы квадратов n натуральных чисел, суммы квадратов первых n четных чисел и суммы квадратов первых n нечетных чисел:
| Сумма квадратов первых n натуральных чисел | [n(n+1)(2n+1)] / 6 |
|---|---|
| Сумма квадратов первых n четных чисел | [2n(n + 1)(2n + 1)] / 3 |
| Сумма квадратов первых n нечетных чисел | [n(2n+1)(2n-1)] / 3 |
Сумма квадратов двух и трех натуральных чисел
Для небольших чисел мы можем напрямую найти квадраты и сложить их, но для больших чисел нам нужно знать идентификатор, чтобы упростить наши вычисления. Пусть a и b будут 2 числа.
Их квадраты равны a 2 и b 2 . Сумма их квадратов равна 2 + б 2 . Мы могли бы получить формулу, используя известное алгебраическое тождество (a+b) 2 = a 2 + b 2 + 2ab. Отсюда заключаем, что а 2 + b 2 = (a + b) 2 – 2ab.
Пусть a, b, c – 3 числа, для которых мы должны найти сумму квадратов. Сумма их квадратов равна a 2 + b 2 + c 2 . Используя известное алгебраическое тождество (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca, мы можем оценить, что a 2 + b 2 + c 2 = (a + b + c) 901 64 2 – 2ab -2bc -2ca.
Сумма квадратов натуральных чисел Доказательство
Давайте научимся вычислять сумму квадратов для больших сумм. Мы можем легко использовать формулу, доступную для нахождения суммы, однако важно выучить вывод формулы суммы квадратов n натуральных чисел: Σn 2 = [n(n+1)(2n+1)] / 6.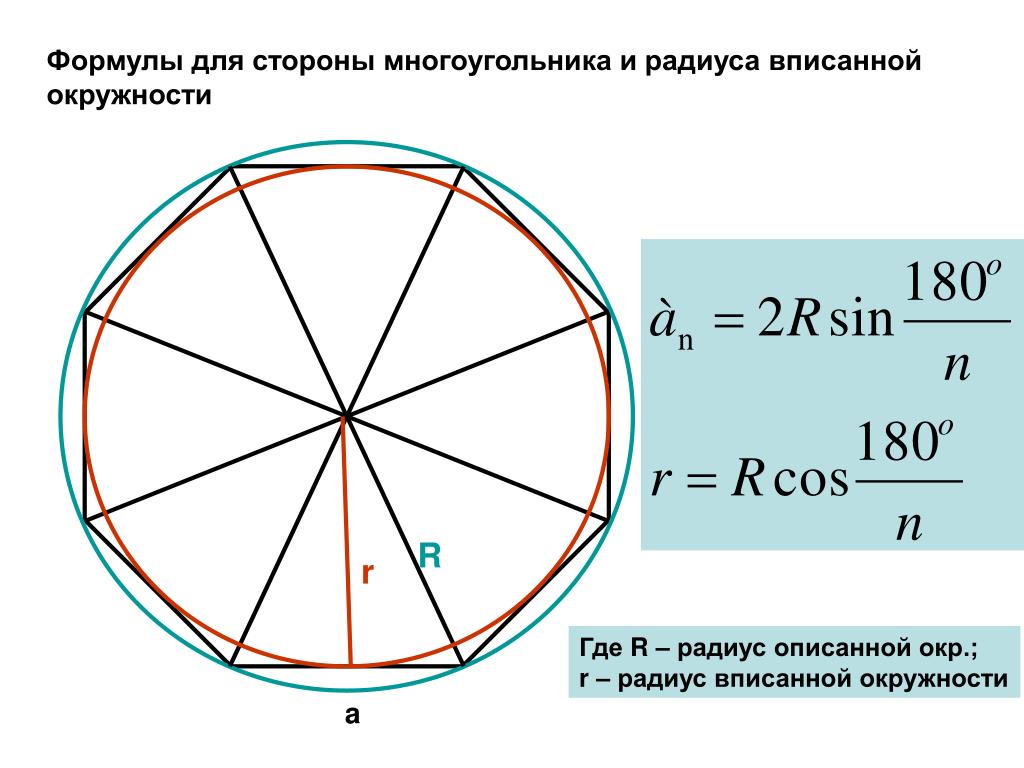
Формулу легко применить, когда известно значение n. Докажем эту формулу, используя принцип математической индукции.
Пусть P(n): 1 2 + 2 2 + 3 2 + … + n 2 = [n(n+1)(2n+1)] / 6
Рассмотрим P(1). левая сторона = 1 2 = 1, правая часть = [1(1+1)(2(1)+1)] / 6 = (1 × 2 × 3) / 6 = 6/6 = 1. Таким образом, левая часть = правая часть. Следовательно, P(1) верно.
Предположим, что P(k) истинно, т. е. 1 2 + 2 2 + 3 2 + … + k 2 = [k(k+1)(2k+1)] / 6 верно. —- (1)
Теперь докажем, что P(k+1) истинно, то есть нужно доказать, что 1 2 + 2 2 + 3 2 + … + (k+1) 2 = [(k+1)(k+2) (2k+3)] / 6 верно.
Рассмотрим LHS = 1 2 + 2 2 + 3 2 + … + (k+1) 2
= 1 2 + 2 9 0164 2 + 3 2 + … + к 2 + (k+1) 2
= [k(k+1)(2k+1)] / 6 + (k+1) 2 — [Используя (1)]
= (k+1)/6 × [k(2k+1) + 6(k+1) ]
= (k+1)/6 × [2k 2 + k + 6k + 6]
= (k+1)/6 × (2k 2 + 7k + 6)
= (k+1)/6 × (2k 901) 64 2 + 4k + 3k + 6)
= (k+1)/6 × [2k(k + 2) + 3(k + 2)]
= = (k+1)/6 × (2k+3)(k + 2)
= [(k+1)(k+2)(2k +3)] / 6
= RHS
Итак, P(k+1) верно.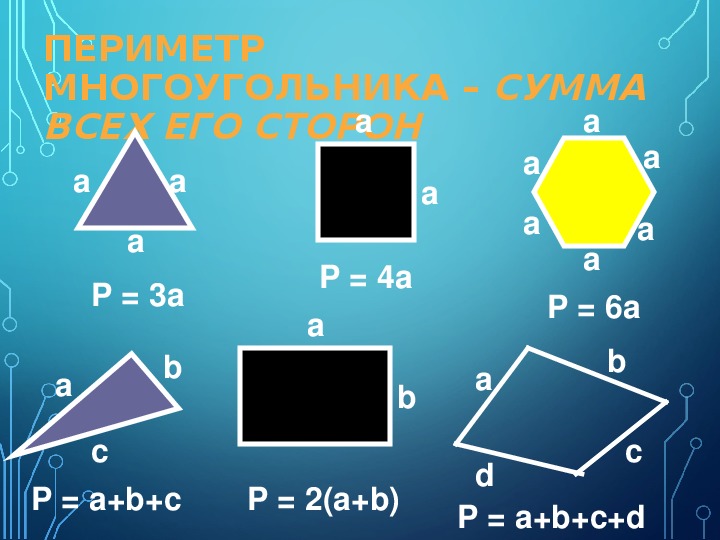
Таким образом, мы можем сказать, что P(n) верно для всех натуральных чисел n. Итак, имеем 1 2 + 2 2 + 3 2 + … + n 2 = [n(n+1)(2n+1)] / 6. Отсюда мы получили формулу суммы квадратов n натуральных чисел.
Альтернативное доказательство:
n 3 – (n-1) 3 = (n- n+1)(n 2 +n(n-1)+ (n-1) 2 )
n 3 – (n-1) 3 = 1(n 2 +n 2 -n+ n 2 + 1 – 2n)
= 3n 2 – 3n + 1
n 3 – (n-1) 3 = 3n 2 – 3n + 1 ———-> (1)
(n-1) 3 – (n-2) 3 = 3 (n-1) 2 – 3(n-1) +1——— -> (2)
(n-2) 3 – (n-3) 3 = 3 (n-2) 2 – 3(n-2) +1———-> (3)
……………….
2 3 – 1 3 = 3 (2) 2 – 3(2) +1
1 3 – 0 3 = 3 (1) 2 – 3(1) +1———->(последний шаг)
(1) + (2) + ( 3) +.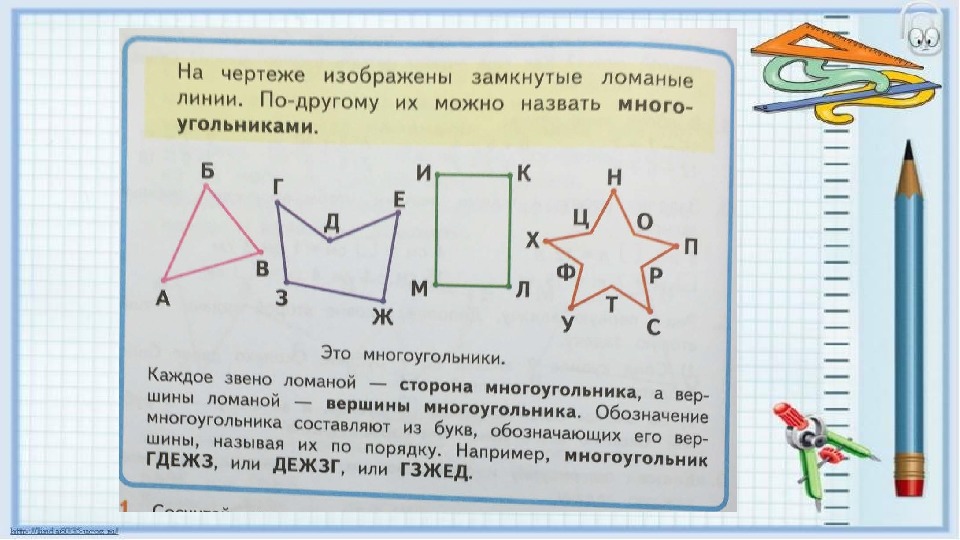
………..+ (последний шаг) ⇒ Складывая все вышеперечисленные шаги, получаем, n 3 – 0 3 = 3 Σ n 2 – 3Σ n + n
n 3 = 3 Σ n 2 – [3n(n+1)/2]+ n [так как Σn = n(n+1)/2 (сумма n натуральных чисел)]
3 Σn 2 = n 3 + [3n(n+1)/2] – n
3 Σ п 2 = n[n 2 + 3(n+1)/2 – 1] — (Принимая n за обычное значение из RHS)
Σ n 2 = (n/3)( n 2 + (3n+3)/2 -1)
= (n/6) (2n 2 + 3n + 1)
Факторизация квадратного выражения,
Σ n 2 = 1 2 + 2 2 + 3 2 + … + n 2 = [n(n+1)(2n+1)] / 6
Сумма квадратов четных натуральных чисел
Четные числа обозначаются 2n, где n — натуральное число. Сумма квадратов первых n четных чисел равна 2 2 + 4 2 + 6 2 + 8 2 + 10 2 + 12 2 + .
…….(2n) 2 . От нас требуется определить n и применить его в известной формуле [2n(n + 1)(2n + 1)] / 3. Выведем формулу из уже изученных формул. Когда n принимает значение от 1 до ∞, мы оцениваем Σ(2n) 2 как, Σ(2 2 . n 2 ) следующим образом.
Σ(2n) 2 = 2 2 .1 2 + 2 2 .2 2 + 2 2 .3 2 + 2 2 .4 2 +…+ 2 2 .n 2 9000 3
Σ(2n) 2 = 2 2 (1 2 + 2 2 + 3 2 + 4 2 … + n 2 )
Σ(2n) 2 = 4 [n(n+1)(2n+1)] / 6 (формула суммы квадратов n натуральных чисел)
Таким образом, Σ(2n) 2 = [2n(n + 1)(2 п + 1)] / 3
Сумма квадратов нечетных натуральных чисел
Нечетные числа обозначаются (2n-1), где n — натуральное число. Сумма квадратов первых n нечетных натуральных чисел равна 1 2 + 3 2 + 5 2 + … + (2n – 1) 2 .
Определим n и применим в известной формуле [n(2n+1)(2n-1)] / 3. Доказательство получим следующим образом: 0164 2 + … + (2н – 1) 2 + (2н) 2 – [2 2 + 4 2 + 6 2 + … + (2n) 2 ]
Σ(2n-1) 2 = (сумма всех последовательных целых чисел от 1 до 2n ) – (сумма квадратов четных чисел)
Σ(2n-1) 2 = [1 2 + 2 2 + 3 2 + … + (2n – 1) 2 9016 5 + (2n) 2 ] – [2 2 + 4 2 + 6 2 + … + (2n) 2 ]
О применении формулы сложения квадратов 2n натуральных чисел и из n четных натуральных чисел получаем;
Σ(2n-1) 2 = [2n(2n+1)(4n+1)] / 6 – [2n(n + 1)(2n + 1)] / 3
= [n(2n+1)(4n+1)] / 3 – [2n(n + 1)(2n + 1) )] / 3
Вынимая общие члены, получаем;
Σ(2n-1) 2 = (n/3) (2n+1) [4n+1 – 2(n+1)]
= (n/3) (2n+1) (4n+1-2n-2)
= [n(2n+1)(2n-1) )] / 3
Σ(2n-1) 2 = [n(2n+1)(2n-1)] / 3
Сумма квадратов в геометрии
Как известно, в прямоугольном треугольнике сумма квадратов перпендикуляра и основания равна квадрату гипотенузы.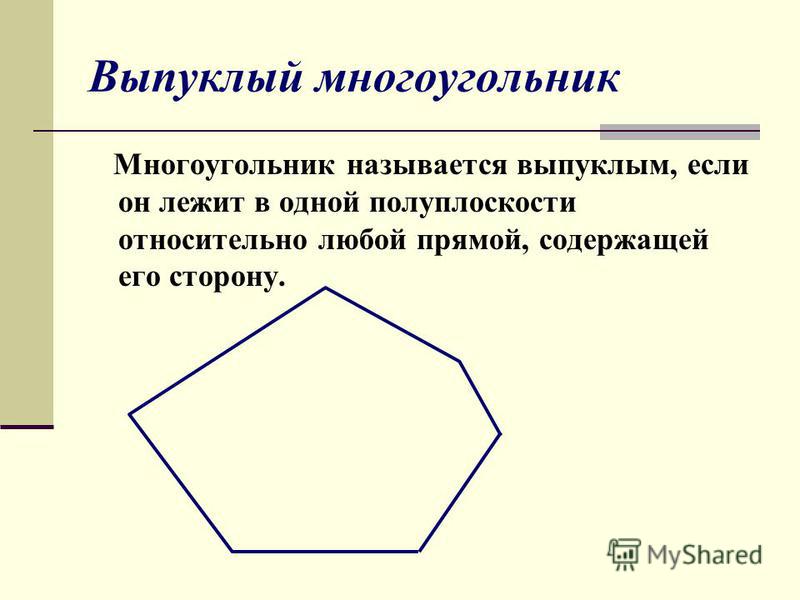
Этот результат известен как теорема Пифагора. Итак, у нас есть сумма квадратов в геометрии, равная
Основание 2 + Перпендикуляр 2 = Гипотенуза 2
Важные замечания о сумме квадратов n натуральных чисел
- Сумма квадратов первых n натуральных чисел равно, Σ n 2 = 1 2 + 2 2 + 3 2 + … + n 2 = [n(n+1)(2n+1)] / 6 9067 9
- Сумма квадратов четных и нечетных натуральных чисел определяется выражением,
- Σ(2n-1) 2 = [n(2n+1)(2n-1)] / 3
- Σ(2n) 2 = [2n(n + 1)(2n + 1)] / 3
- Мы можем вывести формулу суммы квадратов n натуральных чисел, используя принцип математической индукции.
☛Статьи по теме:
- Сумма арифметической последовательности
- Сумма GP
- Формула идеальных квадратов
- Калькулятор суммы квадратов
Часто задаваемые вопросы о сумме квадратов n натуральных чисел
Какова сумма квадратов n натуральных чисел?
Мы можем вычислить сумму квадратов n натуральных чисел по формуле 2 = [n(n+1)(2n+1)] / 6.
Это можно проверить по принципу математической индукции.
Что такое сумма квадратных чисел в алгебре?
Сумма квадратных чисел задается как 2 + b 2 + c 2 +….. до бесконечности. Для суммы квадратов 2-х чисел и 3-х чисел в алгебре мы используем известные алгебраические тождества; Вот некоторые из формул:
- a 2 + b 2 = (a + b) 2 – 2ab
- a 2 + b 2 + c 2 = (a + b + c) 2 – 2ab -2bc -2ca
Как вычислить сумму квадратов натуральных чисел?
- Сумма квадратов n натуральных чисел вычисляется по формуле [n(n+1)(2n+1)]/6.
- Сумма квадратов n нечетных натуральных чисел вычисляется по формуле [n(2n+1)(2n-1)] / 3.
- Сумма квадратов n четных натуральных чисел вычисляется по формуле [2n(n + 1)(2n + 1)] / 3.
Какова сумма квадратов 100 натуральных чисел от 1 до 100?
Для вычисления суммы квадратов чисел от 1 до 100 применим формулу суммы квадратов первых n натуральных чисел, т.
