Геометрия сверла 1×1 | CERATIZIT | WNT
Геометрию сверла определяют количество и положение режущих кромок, стружечных канавок и используемые при этом углы.
По типу выполняемых отверстий различают:
спиральные сверла
Отверстия в сплошном материале выполняются спиральными сверлами. При этом в результате обработки материала образуется цилиндрическая полость. Для изготовления отверстий в диапазоне диаметров до 20 мм и глубиной до 100 мм чаще всего используются именно спиральные сверла.
Метчики
При нарезании резьбы сначала выполняется отверстие в сплошном материале, затем с помощью метчиков нарезается резьба. Эта операция может быть выполнена вручную или на станке. Получаемая внутренняя резьба является стандартизованной, за счет чего она подходит к соответствующей наружной резьбе.
Ступенчатые сверла
Ступенчатые сверла применяются для получения ступенчатых отверстий, позволяющих утапливать соединительные детали (например, головки винтов) в материале.
Геометрия спирального сверла
Геометрия сверла по-разному влияет на размерную точность отверстия и стойкость.
Для понимания, каким образом отдельные аспекты геометрии сверла влияют на факторы, определяющие стойкость или точность сверления, подробно рассмотрим геометрию спирального сверла. Так, например, конструкция сверл, которые имеют не режущие кромки, а сменные многогранные пластины, должна быть оптимизирована с точки зрения отвода стружки, скорости резания и подачи.
- Угол при вершине сверла
- Главные режущие кромки
- Главная задняя поверхность
- Вспомогательная режущая кромка
- Стружечная канавка
- Направляющая ленточка
- Поперечный передний угол
Диаметр спирального сверла
Диаметр спирального сверла уменьшается в области стружечных канавок от вершины сверла в направлении хвостовика.
Конусность составляет от 0,02 до 0,08 мм на 100 мм длины стружечных канавок и уменьшает трение в отверстии. Кроме того, это облегчает эвакуацию стружки.
Угол при вершине – центрирующий элемент спирального сверла
Угол при вершине находится на вершине спирального сверла. Угол измеряется между двумя режущими кромками на вершине.
Чем меньше угол при вершине, тем легче выполняется центрирование в материале. На изогнутых поверхностях это также снижает риск соскальзывания. Для обработки короткостружечных материалов с плохой теплопроводностью выбираются сверла с малым углом при вершине, при этом длинные главные режущие кромки обеспечивают хороший теплоотвод через инструмент. Однако, при малом угле при вершине возможно забивание отверстия или стружечной канавки в результате деформации стружки. Кроме того малый угол при вершине повышает износ режущих кромок.
Для обработки длинностружечных материалов с хорошей теплопроводностью выбирается большой угол при вершине, поскольку он обеспечивает хороший сход стружки и малую силу резания.
Однако при больших углах при вершине выше вероятность увода сверла и получения отверстия увеличенного диаметра.
Большинство спиральных сверл имеют угол при вершине 118 градусов. Угол 90 градусов используется для обработки твердых, изнашивающихся пластмасс, 130 градусов – для мягких и прочных материалов и 140 градусов – для длинностружечных легких сплавов.
Главные режущие кромки спирального сверла – отвечают за производительность
Спиральное сверло всегда имеет две главные режущие кромки, соединенные перемычкой. Главные режущие кромки обеспечивают собственно процесс сверления. Удлиненные режущие кромки позволяют добиться более высокой производительности по сравнению с короткими режущими кромками.
Перемычка спирального сверла – чем короче, тем лучше
Перемычка находится в центре вершины сверла и не оказывает режущего воздействия. Она только давит на поверхность обрабатываемой детали и создает трение и, в сущности, затрудняет процесс сверления.
Соответствующие технологии заточки позволяют уменьшить длину перемычки. Эта так называемая подточка или перекрестная шлифовка значительно уменьшает силы трения и, следовательно, снижает требуемое усилие подачи. В то же время улучшается центрование вершины сверла на обрабатываемой детали.
Профиль канавки (спиральная канавка) спирального сверла – отвечает за стойкость
Спиральное сверло имеет две расположенные друг напротив друга спиральные стружечные канавки, обеспечивающие отвод стружки и подачу СОЖ. Как правило, они изготавливаются в заготовке врезным шлифованием, фрезерованием или завальцовкой. Широкие профили канавок имеют меньшую глубину и позволяют реализовать более значительный диаметр сердцевины сверла.
Плохой отвод стружки означает повышенное выделение тепла, что, в свою очередь, может привести к расплавлению и, в конечном итоге, к поломке сверла.
Большое скопление стружки может вызвать радиальное биение сверла и отразиться на качестве отверстия, стойкости, а также надежности сверла и привести к поломке сверла или режущей пластины.
Чем шире профиль канавки, тем эффективнее отвод стружки.
Сердцевина – жесткость спирального сверла
Диаметр сердцевины имеет решающее значение для жесткости спирального сверла. Спиральные сверла с большим диаметром сердцевины (толстой сердцевиной) отличаются более высокой жесткостью и поэтому подходят для повышенных крутящих моментов и обработки материалов высокой твердости.
Направляющие ленточки и вспомогательные кромки спирального сверла – отвечают за точность вращения и качество стенок отверстия
- Главная режущая кромка
- Задняя поверхность
- Вспомогательная режущая кромка
Посредством затыловки вдоль стружечных канавок формируются направляющие ленточки. В зависимости от диаметра сверла они имеют ширину от 0,1 до 5 мм и обеспечивают нужное направление сверла в отверстии. От их состояния в значительной степени зависит качество стенок отверстия.
Вспомогательная кромка образует переход от направляющей ленточки к стружечной канавке.
Длина направляющих ленточек и вспомогательных кромок в значительной степени зависит от угла наклона винтовых канавок.
Угол наклона винтовых канавок (угол спирали) спирального сверла определяет применяемость для разных материалов
Угол спирали, называемый также углом наклона винтовых канавок, образуется направлением канавки и осью сверла. Он определяет величину угла резания на главных режущих кромках и, следовательно, процесс формирования стружки.
Увеличенный угол наклона винтовых канавок обеспечивает эффективный отвод стружки при обработке мягких, длинностружечных материалов. Малые углы наклона винтовых канавок, напротив, применяются при обработке твердых, короткостружечных материалов.
Спиральные сверла с очень малым углом наклона винтовых канавок (10°–19°) имеют вытянутую спираль. Спиральные сверла с большим углом наклона винтовых канавок (27°–45°), напротив, имеют сжатую, короткую спираль.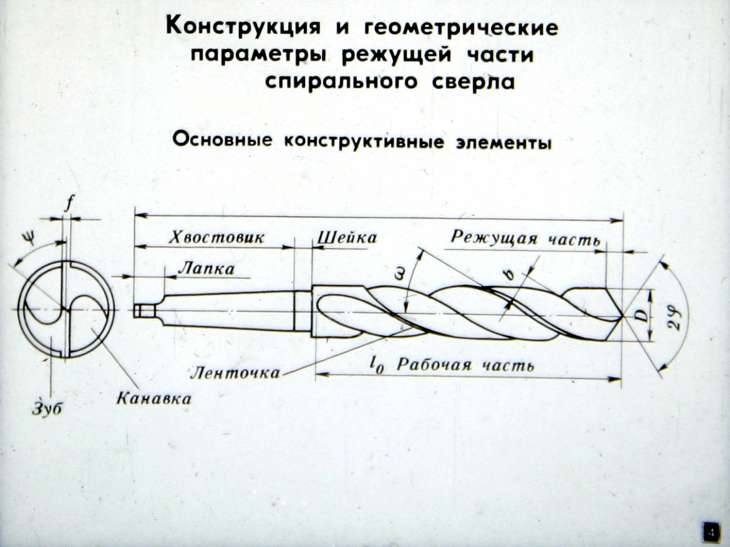
Выбор сверла в зависимости от свойств обрабатываемого материала – 3 типа
Техническое руководство DIN по сверлам и зенковкам в стандарте DIN 1836 в зависимости от области применения выделяет три типа N, H и W:
- Тип N: нормальная спираль для материалов средней твердости, таких как конструкционные стали, цветные металлы и чугун. Не подходит для мягких материалов
- Тип H: вытянутая спираль для твердых, короткостружечных, хрупких и вязкотвердых материалов, например, для стали, твердых пластмасс, плексигласа или слоистых прессованных материалов
- Тип W:
Скорость резания и износ
При правильно выбранных режимах резания происходит равномерный износ по всей поверхности.
Неравномерный износ возможен при слишком высокой скорости резания, слишком большой подаче или обработке слишком твердого материала. В этом случае требуется переточка сверла по задней поверхности до полного устранения износа главной режущей кромки, перемычки и направляющей ленточки. Если износ направляющей ленточки не устраняется, происходит заклинивание сверла.
Геометрия стружколома сверла (+Видео) – Журнал «Твердый сплав»
- 8 лет назад
Как уже было отмечено ранее в этом материале, контроль стружкообразования – это один из важнейших пунктов, которые при обработке учитываются в первую очередь. Более того, необходимо уделять должное внимание геометрии, о чем и пойдет речь в данной статье.
Несмотря на то, что в тематической литературе геометрия стружколома рассматривается довольно часто, статья выделяется среди подобных материалов. Автор, основываясь на накопленном опыте, предлагает свою собственную подборку, позволяющую ознакомиться с основными аспектами и взглянуть на геометрию инструмента совершенно под другим углом.
Для начала рассмотрим основные параметры геометрии режущей части сверла.
Занижение задней поверхности
Занижение задней поверхности – это свободное пространство между режущей кромкой и наружным диаметром. Угол занижения задней поверхности может быть увеличен, правда в ущерб прочности режущей кромки, и в таких случаях наилучшие показатели достигаются при обработке мягких материалов. В случае использования широкого угла следует помнить о возникновении нежелательного воздействия на вершину сверла, что необходимо учитывать на высоких скоростях резания.
Угол наклона винтовой канавки
Угол между осью сверла и его спиралями называется углом наклона винтовых канавок. Значения угла спирали являются важнейшим фактором оптимального удаления стружки.
Сверло с широким углом наклона рекомендовано для обработки материалов низкой прочности, при этом диапазон стандартных размеров угла составляет 15-40°.
Длина винтовой канавки
Длина винтовой канавки измеряется от крайней точки вершины сверла, где расположены все кромки, до места, где канавки заканчиваются.
Длина канавок должна превышать глубину отверстия, чтобы стружка не скапливалась и не застревала внутри. Автор рекомендует использовать максимально возможную длину канавок.
Канавка с двумя полями
Двойной дизайн канавки обеспечивает стабильность и позволяет сверлить отверстие с повышенной точностью.
В некоторых случаях для обработки вязких материалов следует выбрать геометрию с уменьшенными полями, например для того, чтобы улучшить сверление алюминия.
Угол при вершине
Основное предназначение заднего угла заключается в уменьшении контакта между сверлом и обрабатываемым материалом.
Передний угол может быть положительным, нулевым или отрицательным, в зависимости от расположения к оси сверла. Обычно этот угол положительный и составляет примерно 12º.
Источник материала: перевод статьи
Chip breaking geometries in drilling,
Compositemachining.
org
Автор статьи-оригинала:
Хосе (JOSE)
Ручная заточка спиральных сверл
Предлагаем вам ознакомится с обучающим видео на русском языке, найденном нами на YouTube
Основы геометрии сверла | ЦЕРАТИЗИТ | WNT
Геометрия сверла – это количество и положение режущих кромок сверла, стружечных канавок и используемый угол.
В зависимости от типа создаваемого отверстия различают:
Спиральное сверло
Сверление в твердом материале выполняется спиральным сверлом. Цилиндрическое полое тело создается путем механической обработки материала. Для сверления отверстий диаметром до 20 мм и глубиной до 100 мм чаще всего используется спиральное сверло.
Нажмите
При нарезании резьбы сначала создается сплошное отверстие, затем с помощью метчиков нарезается резьба.
Этот шаг можно выполнить вручную или с помощью машины. Полученная внутренняя резьба стандартизирована, чтобы соответствовать соответствующей внешней резьбе.
Ступенчатая дрель
Ступенчатое сверло формирует ступенчатое отверстие, чтобы можно было позволить соединению (например, головке винта) погрузиться в материал. Последующая обработка, такая как развертывание или зенкерование, не требуется.
Геометрия спирального сверла
Различные геометрии влияют на точность размеров отверстия и срок службы сверла.
Чтобы понять, какой аспект геометрии сверла влияет на какой фактор стойкости инструмента или допусков сверла, можно подробно рассмотреть геометрию спирального сверла в качестве примера. Сверла со сменными пластинами вместо режущих кромок сталкиваются с той же проблемой, заключающейся в достижении идеального баланса между удалением стружки, скоростью резания и скоростью подачи.
- Угол при вершине
- Основные режущие кромки
- Главный фланг
- Вторичная режущая кромка
- Стружечная канавка
- Направляющая земля
- Боковой передний угол
Диаметр спирального сверла
Диаметр спирального сверла сужается в области стружечных канавок от кончика сверла к хвостовику. Конусность составляет от 0,02 до 0,08 мм при длине стружечной канавки 100 мм и снижает трение в отверстии. Это также облегчает сход стружки.
Угол при вершине – центрирование спирального сверла
Угол вершины расположен на головке спирального сверла. Угол измеряется между обеими режущими кромками на острие.
Чем меньше угол при вершине, тем легче центрирование в материале. Таким образом, на изогнутых поверхностях риск поскользнуться также ниже. Небольшие углы при вершине лучше подходят для обработки материалов с плохой теплопроводностью и короткой стружкой; длинные основные режущие кромки обеспечивают хороший отвод тепла от инструмента.
Однако, если угол при вершине слишком мал, отверстие или канавка для стружки могут быть заблокированы из-за сжатия стружки. Небольшой угол при вершине также увеличивает износ режущей кромки.
Большой угол при вершине используется для материалов с хорошей теплопроводностью или для материалов, дающих длинную стружку, так как это приводит к отличному сходу стружки и низкому усилию резания. Однако большой угол при вершине приводит к более легкому блужданию сверла и большему отверстию.
Большинство спиральных сверл имеют угол при вершине 118 градусов. 90 градусов используются для твердых пластмасс, подверженных износу, 130 градусов для мягких и прочных материалов и 140 градусов для легких металлов, дающих длинную стружку.
Основные режущие кромки спирального сверла – отвечают за производительность обработки
На спиральном сверле всегда присутствуют две основные режущие кромки, которые соединены долотом. Основные режущие кромки обеспечивают фактический процесс сверления .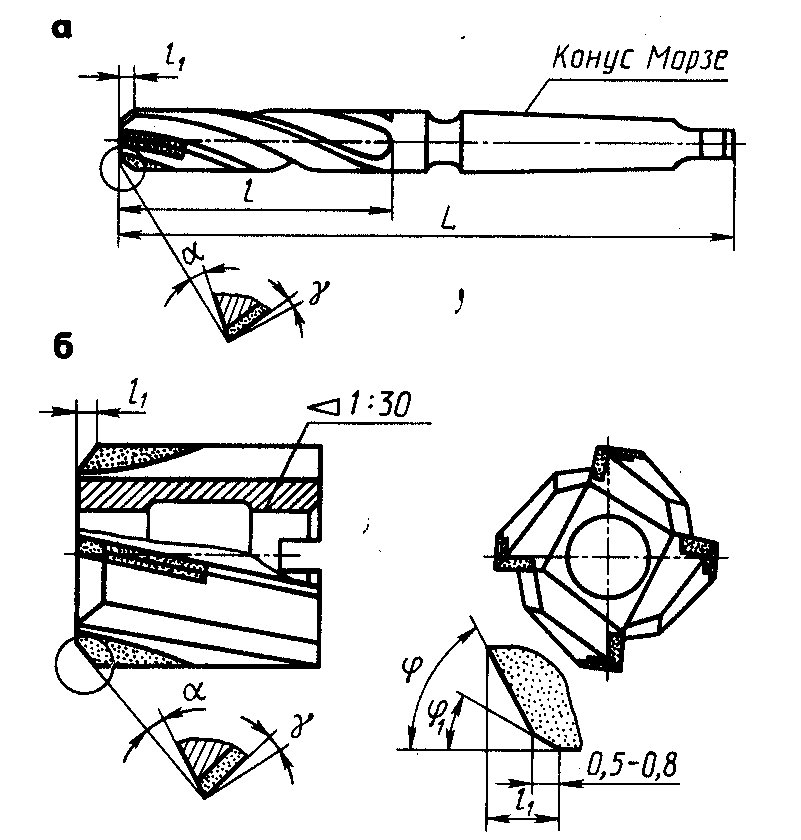
По сравнению с короткими режущими кромками длинные режущие кромки обеспечивают лучшую производительность обработки.
Долото спирального сверла – чем короче, тем лучше
Режущая кромка расположена в центре наконечника сверла и не имеет режущего эффекта. Он оказывает давление и трение на заготовку и поэтому является помехой в процессе сверления. Длина лезвия долота может быть уменьшена с помощью соответствующего процесса шлифования. Это утончение или поперечное шлифование приводит к значительному снижению сил трения и, следовательно, к уменьшению необходимого усилия подачи. В то же время острие сверла лучше центрируется в заготовке.
Профиль канавки (спиральная канавка) спирального сверла – отвечает за стойкость инструмента
Спиральное сверло имеет две противоположные спиральные канавки для стружки, которые обеспечивают удаление стружки и подачу СОЖ. Их обычно измельчают, фрезеруют или скатывают в заготовку.
Широкие профили канавки более плоские и позволяют сверлить больший диаметр.
Плохой отвод стружки приводит к повышенному выделению тепла, что, в свою очередь, может привести к отжигу и, в конечном итоге, к поломке сверла.
Сильная блокировка стружки может вызвать радиальные движения сверла и повлиять на качество отверстия, срок службы инструмента и надежность сверла. Это также может привести к поломке сверла и пластины. Чем шире профиль канавки, тем лучше удаление стружки.
Core – стабильность спирального сверла
Толщина сердцевины является решающим фактором стабильности спирального сверла . Спиральные сверла с большим (толстым) диаметром стержня обеспечивают большую стабильность и поэтому подходят для более высоких крутящих моментов и более твердых материалов.
Направляющие кромки и вторичные режущие кромки спирального сверла – отвечают за точность радиального биения и качество стенки отверстия
- Основная режущая кромка
- Фланг
- Вторичная режущая кромка
Направляющие лезвия являются результатом зачистки вдоль стружечных канавок.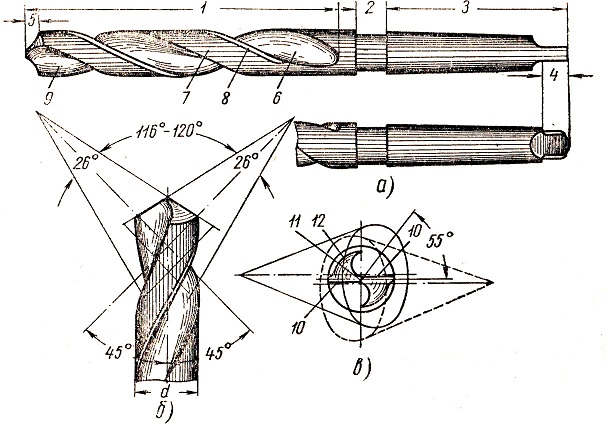
В зависимости от диаметра сверла они имеют ширину от 0,1 до 5 мм и помогают вести сверло в отверстии. Качество стенки скважины во многом зависит от ее состава.
Вспомогательная режущая кромка образует переход от направляющей к канавке для стружки. Он разрыхляет и срезает стружку, застрявшую в материале .
Длина направляющих и вспомогательных режущих кромок сильно зависит от угла наклона спирали.
Угол наклона спирального сверла – определяет область применения в зависимости от материала
Угол подъема спирали формируется направлением канавки и осью сверла. Он определяет размер переднего угла на основных режущих кромках и, таким образом, процесс формирования стружки .
Больший угол наклона спирали обеспечивает эффективный отвод стружки при работе с мягкими материалами, дающими длинную стружку. Напротив, меньшие углы наклона спирали используются для твердых материалов с короткой стружкой.
Спиральные сверла с очень малым углом наклона спирали (10° – 19°) имеют вытянутую спираль. Напротив, спиральные сверла с большим углом наклона спирали (27° – 45°) имеют сжатую короткую спираль. Спиральные сверла с нормальной спиралью имеют угол наклона спирали от 19° до 40°.
Какое сверло для какого материала – три вида
В руководстве DIN для сверл и зенкеров разделение групп применения на три типа N, H и W определено согласно DIN1836: общестроительные стали, цветные металлы и чугун. Не подходит для мягких материалов
Скорость резания и износ
Если выбраны правильные режимы резания, износ инструмента будет равномерным.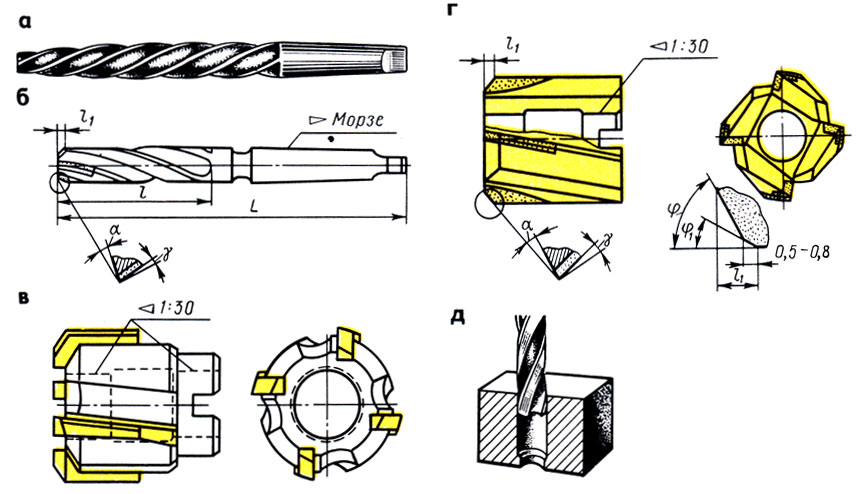
Неравномерный износ может произойти, если скорость резания слишком высока, подача слишком велика или материал слишком твердый. Затем сверло необходимо перетачивать по боковой поверхности до тех пор, пока не будет полностью устранен износ основной режущей кромки, режущей кромки и направляющей кромки. Если износ направляющей кромки не устранен, сверло заклинит.
Рабочие листы по геометрии
Добро пожаловать на страницу с рабочими листами по геометрии на сайте Math-Drills.com, где мы считаем, что нет ничего плохого в том, чтобы быть квадратным! Эта страница включает рабочие листы по геометрии углов, координатной геометрии, треугольников, четырехугольников, преобразований и трехмерных геометрических листов.
Достаньте эти линейки, транспортиры и циркуль, потому что у нас есть отличные рабочие листы по геометрии! Четырехугольники нужно вырезать, измерять, складывать, сравнивать и даже писать на них. Они могут быть весьма полезны при обучении всевозможным понятиям, связанным с четырехугольниками.
Прямо под ними вы найдете рабочие листы, предназначенные для угловой геометрии. Также см. страницу измерений для получения дополнительных таблиц углов. Основная часть этой страницы посвящена трансформациям. Трансформационная геометрия — одна из тех тем, которые могут быть действительно интересны для студентов, и у нас есть достаточно рабочих листов по этой теме геометрии, чтобы ваши студенты были заняты часами.
Не пропустите сложный, но интересный мир соединяющихся кубиков внизу этой страницы. Вы можете встретить нескольких будущих художников, когда будете использовать эти рабочие листы со студентами.
Самые популярные рабочие листы по геометрии на этой неделе просмотров на этой неделе
)Классификация треугольников по свойствам углов и сторон (отметки, включенные на страницу вопроса) ( 350 просмотров на этой неделе )Определение масштабного коэффициента между двумя фигурами и определение недостающих длин (масштабные коэффициенты с интервалом 0,5) ( 272 просмотров на этой неделе )Знакомство с фигурами .
Наборы форм Набор четырехугольников можно использовать для ряда действий, связанных с классификацией и распознаванием четырехугольников или для определения свойств четырехугольников (например, сумма внутренних углов составляет 360 градусов). Распечатки танграма полезны в занятиях танграмом. Существует несколько вариантов печати танграмм в зависимости от вашего принтера, и каждый вариант включает в себя большую версию и уменьшенную версию. Если вы знаете кого-то с подходящей пилой, вы можете использовать танграм для печати в качестве шаблона на таком материале, как фанера в четверть дюйма; затем просто отшлифуйте и покрасьте детали.
Набор четырехугольников Танграмы
Идентификация фигурОпределение правильных фигур от треугольников до восьмиугольников
Рабочие листы по геометрии углов
Рабочие листы по геометрии углов для именования углов и взаимосвязей углов.
Если вы ищете рабочие листы для измерения углов, посмотрите страницу измерений
Именованные уголкиИменование простых углов Именование всех углов
Соотношение угловДополнительные углы Дополнительные углы Вертикальные углы Внутренние альтернативные углы Внешние альтернативные углы Альтернативные углы Соответствующие углы Со-внутренние углы Трансверсали
Геометрия координатных точек
Рабочие листы по геометрии координатных точек, чтобы помочь учащимся изучить декартову плоскость.
Нанесение точек координат во всех квадрантах Нанесение координатных точек в положительные квадранты x Построение координатных точек в положительных квадрантах и
Картезианское искусство
На веб-сайте Math-Drills разбросано множество других сюжетов картезианского искусства, поскольку многие из них связаны с праздником. Чтобы быстро их найти, воспользуйтесь поиском.
Картезианское искусство от Math-Drills
Расстояние и площадь координатной плоскости
Вычисление пифагорейских расстояний координатных точек Вычисление периметра и площади треугольников на координатных плоскостях Вычисление периметра и площади четырехугольников на координатных плоскостях Вычисление периметра и площади треугольников и четырехугольников на координатных плоскостях
Треугольники и теорема Пифагора
Рабочие листы для классификации треугольников по свойствам сторон и углов и для работы с теоремой Пифагора.
Если вы заинтересованы в том, чтобы учащиеся самостоятельно измеряли углы и стороны, лучше всего использовать версии без меток. Отмеченные версии будут указывать прямые и тупые углы и равные стороны.
Классификация треугольников по свойствам сторон Классификация треугольников от Angle Properties Классификация треугольников по свойствам сторон и углов Классификация треугольников по свойствам сторон (без меток) Классификация треугольников по свойствам углов (без меток) Классификация треугольников по свойствам сторон и углов (без меток)
Теорема Пифагора
Катет (множественное число катети) относится к стороне прямоугольного треугольника, отличной от гипотенузы.
Вычислить Гипотенузу Используя теорему Пифагора (без вращения) Вычислить гипотенузу по теореме Пифагора Вычислить Катет Используя теорему Пифагора (без вращения) Вычислите катет , используя теорему Пифагора Вычислите любую сторону , используя теорему Пифагора (без вращения) Вычислите любую сторону , используя теорему Пифагора
Четырехугольники
Рабочие листы для классификации четырехугольников.
Четырехугольники интересны для классификации. Их классификация основана на нескольких атрибутах, и большинство четырехугольников можно классифицировать как более чем одну форму. Квадрат, например, является также параллелограммом, ромбом, прямоугольником и воздушным змеем. Краткий обзор всех четырехугольников выглядит следующим образом: четырехугольники имеют четыре стороны. В квадрате 9Углы 0 градусов и стороны одинаковой длины. Прямоугольник имеет углы 90 градусов, но длины сторон не обязательно должны быть равными. Стороны ромба равны, но углы не обязательно должны быть 90 градусов. У параллелограмма обе пары противоположных сторон равны и параллельны, и обе пары противоположных углов равны. У трапеции должна быть параллельна только одна пара противоположных сторон. Воздушный змей имеет две пары сторон одинаковой длины, где каждая пара соединена / примыкает, а не напротив друг друга. Иногда включается галстук-бабочка, представляющая собой сложный четырехугольник с двумя пересекающимися сторонами, но их легко узнать.
Любой другой четырехугольник можно с уверенностью назвать четырехугольником, если он не соответствует ни одному из критериев более конкретной классификации.
Классификация простых четырехугольников Классификация всех четырехугольников Классификация всех четырехугольников (+ вращение)
Рабочие листы трансформации
Рабочие листы трансформаций для практики переводов, отражений, поворотов и расширений.
Вот два простых и быстрых способа проверить ответы учащихся на рабочих листах по трансформационной геометрии, приведенных ниже. Во-первых, вы можете выровнять страницу учащегося и страницу ответов и поднести их к свету. Слегка переместив/сдвинув страницы, вы увидите, верны ли ответы учащегося. Держите страницу учащегося наверху и отмечайте ее или оставляйте отзыв по мере необходимости. Второй способ — сделать копию страницы ответов на диапозитиве. Наложите прозрачность на страницу учащегося и при необходимости переверните ее, чтобы отметить или оставить отзыв.
Переводы, также известные как скольжение, представляют собой способ математического описания того, как что-то движется на декартовой плоскости. В переводах каждая вершина и сегмент линии перемещаются одинаково, поэтому результирующая форма конгруэнтна оригиналу.
Трансляция 3-х вершин до 3-х единиц. Трансляция 3 вершин до 6 единиц. Трансляция 3-х вершин до 25 единиц. Трансляция 4 вершин до 6 единиц. Трансляция 5 вершин до 6 единиц. Двухэтапный Перенос 3 вершин до 6 единиц. Двухэтапный Перенос 4 вершин до 6 единиц. Трехэтапный Перенос 3 вершин на 6 единиц. Трехэтапный Перенос 4 вершин на 6 единиц.
Отражения Подумайте об этом: отражение фигур по горизонтальным или вертикальным линиям на самом деле довольно прямолинейно, особенно если задействована сетка. Начните с одной из исходных точек/вершин и измерьте расстояние до отражающей линии.
Обратите внимание, что вы должны измерять перпендикулярно или 90 градусов к линии, поэтому легче с вертикальными или горизонтальными отражающими линиями, чем с диагональными линиями. Отмерьте 90 градусов на другой стороне отражающей линии, конечно же, такое же расстояние, и поставьте точку, представляющую отраженную вершину. После того, как вы сделали это для всех вершин, вы просто рисуете сегменты линии, и ваша отраженная форма будет завершена.
Отражение также может быть таким же простым, как складывание бумаги. Сложите бумагу по отражающей линии и поднесите бумагу к свету. Лучше всего на окне, потому что у вас также будет поверхность, на которой можно писать. Отмечайте только вершины, не пытайтесь нарисовать всю фигуру. Разверните бумагу и с помощью карандаша и линейки нарисуйте отрезки между вершинами.
Отражение 3 вершин более x = 0 и y = 0 Отражение 4 вершин свыше x = 0 и y = 0 Отражение 5 вершин свыше x = 0 и y = 0 Отражение 3 вершин по различным линиям Отражение 4 вершин по различным линиям Отражение 5 вершин по различным линиям Двухшаговый Отражение 3 вершин по различным линиям Двухшаговый Отражение 4 вершин по различным линиям Трехшаговый Отражение 3 вершин по разным линиям Трехшаговый Отражение 4 вершин по различным линиям
Обороты Вот идея, как совершать обороты без измерения.
Лучше всего он работает на сетке и с поворотом на 90 или 180 градусов. Вам понадобится чистый лист для диапроектора или другой подходящий прозрачный пластиковый лист и ручка, которой можно рисовать на странице. Лучше всего подходят одноразовые ручки, потому что пластиковый лист можно мыть и использовать повторно. Поместите лист поверх осей координат с фигурой, которую нужно повернуть. С помощью ручки сделайте небольшой крест, чтобы показать 9Максимально точные оси 0236 x и y . Также отметьте вершины фигуры, которую нужно повернуть. Используя пластиковый лист, выполните вращение, снова совместив крест с осями. Выберите одну вершину и отметьте ее на бумаге, удерживая пластиковый лист на месте, но перевернув его достаточно, чтобы получить отметку на бумаге. Сделайте то же самое с другими вершинами, затем снимите пластиковый лист и соедините вершины отрезками с помощью линейки.
Вращение 3 вершин вокруг Происхождение Начиная с квадранта I Вращение 4 вершин вокруг начала координат , начиная с квадранта I Вращение 5 вершин вокруг начала координат , начиная с квадранта I Вращение 3 вершин вокруг начала координат Вращение 4 вершин вокруг начала координат Вращение 5 вершин вокруг начала координат Вращение 3 вершин вокруг любой точки Вращение 4 вершин вокруг любой точки Вращение 5 вершин вокруг любой точки Двухэтапное вращение трех вершин вокруг любой точки Двухэтапное вращение 4 вершин вокруг любой точки Двухэтапное вращение 5 вершин вокруг любой точки Трехступенчатое вращение трех вершин вокруг любой точки Трехступенчатое вращение 4 вершин вокруг любой точки Трехступенчатое вращение 5 вершин вокруг любой точки
Расширения и масштабные коэффициентыРасширение с использованием центра (0, 0) Расширения с использованием различных центров Определите масштабные коэффициенты прямоугольников (целые числа) Определите масштабные коэффициенты прямоугольников (0,5 интервала) Определите масштабные коэффициенты прямоугольников (0,1 интервала) Определите масштабные коэффициенты треугольников (целые числа) Определить масштабные коэффициенты треугольников (0,5 интервала) Определить масштабные коэффициенты треугольников (интервалы 0,1) Определить масштабные коэффициенты прямоугольников и треугольников (целые числа) Определить масштабные коэффициенты прямоугольников и треугольников (0,5 интервала) Определить масштабные коэффициенты треугольников прямоугольников (интервалы 0,1)
Смешанные преобразованияДвухэтапные преобразования Трехэтапные преобразования
Рабочие листы по построению
Рабочие листы по построению биссектрисы, перпендикуляра и центра треугольника.
Удивительно, чего можно добиться с помощью циркуля, линейки и карандаша. В этом разделе учащиеся будут заниматься математикой, как это делал Евклид более 2000 лет назад. Это будет не только урок истории, но и учащиеся получат ценные навыки, которые они смогут использовать в дальнейших занятиях по математике.
Построение середины и биссектрисы на отрезках и углахСередины на сегментах горизонтальной линии Биссектрисы на горизонтальных отрезках Биссектрисы на повернутых отрезках прямой Биссектрисы угла (углы без поворота) Биссектрисы угла (случайно повернутые углы)
Построение перпендикулярных линийПостройте перпендикулярные линии через точки на отрезке линии Постройте перпендикулярные линии через точки не на сегменте линии Построение перпендикулярных линий через точки на сегменте линии (сегменты вращаются случайным образом) Построить перпендикулярные линии через точки не на сегменте линии (сегменты поворачиваются случайным образом)
Построение центров треугольниковЦентроиды остроугольных треугольников Центроиды для смешанных остроугольных и тупоугольных треугольников Ортоцентры остроугольных треугольников Ортоцентры смешанных остроугольных и тупоугольных треугольников Инцентры для остроугольных треугольников Инцентры для смешанных остроугольных и тупоугольных треугольников Центры окружности остроугольных треугольников Центры окружностей для смешанных остроугольных и тупоугольных треугольников Все центры острых треугольников Все центры смешанных остроугольных и тупоугольных треугольников
Рабочие листы трехмерной геометрии
Рабочие листы трехмерной геометрии, основанные на соединении кубов и рабочих листов для классификации трехмерных фигур.
Соединяющие кубики могут быть мощным инструментом для развития у учащихся пространственного чувства. Первые два листа ниже сложны даже для взрослых, но после небольшой практики учащиеся будут создавать структуры гораздо более сложные, чем приведенные ниже. Используйте бумагу с изометрической сеткой и квадратную миллиметровку или точечную бумагу, чтобы помочь учащимся создавать трехмерные эскизы соединяющихся кубов и видов сбоку структур.
Виды сбоку на соединяющиеся кубические структуры Создавайте соединительные кубические структуры
Классификация трехмерных фигурКлассифицировать призмы Классифицировать пирамиды Классифицировать призмы и пирамиды
Сетки объемных фигур . В этом разделе содержится ряд сетей, которые учащиеся могут использовать для построения связанных трехмерных тел. Включены все платоновы тела и многие архимедовы тела.
Ножницы, немного скотча и немного ловкости — вот и все, что нужно. Для чего-то более существенного сначала скопируйте или распечатайте сети на картоне. Вы также можете проверить настройки печати, чтобы убедиться, что вы печатаете в «фактическом размере», а не по размеру страницы, чтобы не было искажений.
Сети платоновых и архимедовых тел Сети всех платоновых тел Сети некоторых архимедовых тел Сеть тетраэдра Чистый куб Сеть октаэдра Сеть додекаэдра (Версия 1) Сеть додекаэдра (Версия 2) Сеть икосаэдра Сеть усеченного тетраэдра Сеть кубооктаэдра Сеть усеченного куба Сеть усеченного октаэдра Сеть ромбокубооктаэдра Сеть усеченного кубооктаэдра Сеть курносого куба Сеть икосододекаэдра
Тригонометрические отношения, также известные как SOHCAHTOA
Тригонометрический Соотношения Тригонометрические отношения полезны при определении размеров прямоугольных треугольников. Три основных соотношения суммируются аббревиатурой SOHCATOA.
