формула, примеры расчета с пояснениями / Справочник :: Бингоскул
Рассмотрим, как рассчитать выигрыш в силе при использовании простейших механизмов, которые люди тысячелетиями используют для перемещения тяжёлых предметов: рычаги, наклонные поверхности, блоки. Первые применяются для перемещения массивных предметов с применением сил, которые имеют меньший за них вес; вторые – облегчают передвижение и подъём тел.
О простейших механизмах
Тяжелые вещи люди издревле поднимали при помощи:
- рычагов – жёстких балок, способных вращаться вокруг точки опоры;
- блоков – колёс с желобами для скольжения верёвки, ремня, троса.
Части рычага до и после точки опоры называются плечами:
- коротким – плечо приложения усилия;
- длинным – плечо приложения силы.
Механизм создаёт большее физическое усилие на коротком плече, чем сила, прилагаемая к длинному. На практике в его качестве применяются длинные (до нескольких метров) жёсткие деревянные балки, брус, металлические трубы.
Он же стал прообразом первых механических весов.
Рычаг будет находиться в равновесии до момента, пока вращающий его по часовой стрелке момент сил равняется силе, вращающей его в обратном направлении (по модулю). Если у механизма разные оси вращения – расстояние от точки опоры до места прикладывания усилия, такой рычаг даёт выигрыш в силе, расчёт которого проводится по формуле:
l2 : l1.
F1 = F2 * l2 : l1, здесь:
- F1 и F2 – величины усилий;
- l1 и l2 – длина первого и второго плеча.
В данном случае l1 2
Действительно, жёсткий рычаг с отличающейся в десятки раз длиной плеч сведёт к минимуму прикладываемую для передвижения либо подъёма предмета силу, но выигрыш в работе он не обеспечит. Во сколько раз легче будет подъем, ровно на столько вещь придётся переместить дальше, а значит выигрыша в работе не получить. Докажем это.
Докажем это.
Выполняемая работа пропорциональна прикладываемой силе, пройденному телами расстоянию на угол поворота.
Отсюда выплывает, что энергия в системе ниоткуда не появляется и бесследно не исчезает, только переходит из одной формы в иную. Часть – уходит на нагрев тел вследствие их трения.
Примеры рычага: плоскогубцы, ножницы, клещи, ручной тормоз авто.
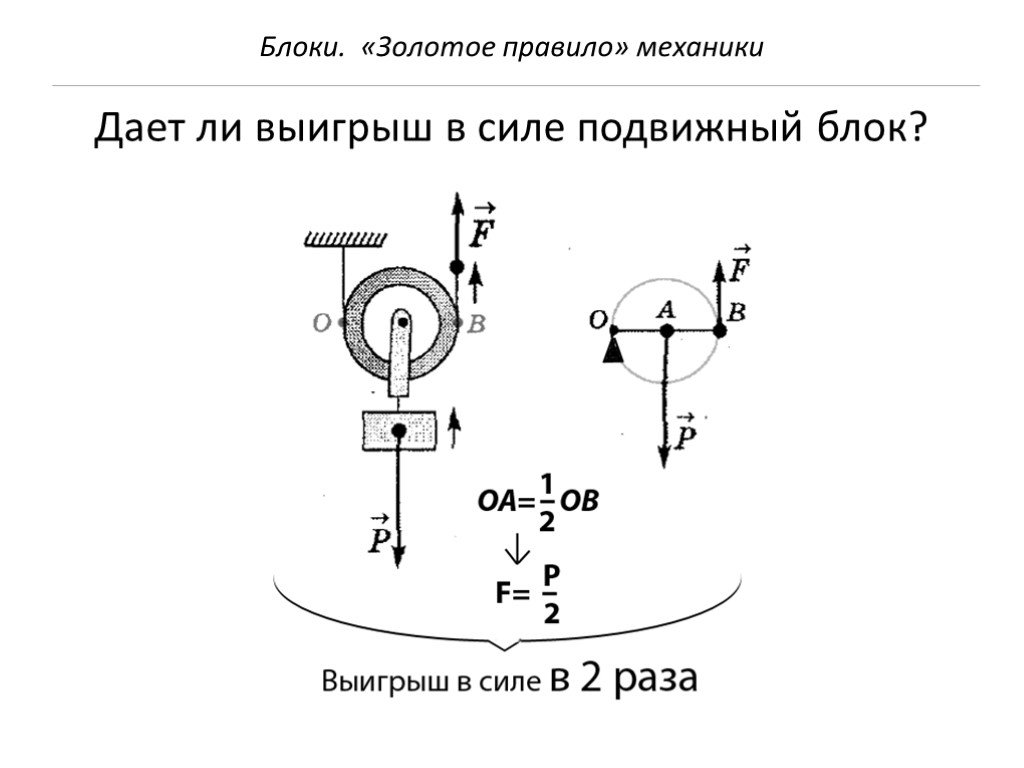
Какой выигрыш в силе дает подвижный блок
Различают неподвижные и подвижные блоки – колёса с продольными канавами для верёвки, крепящиеся на ось. Первые изменяют направление воздействия приложенной силы, не предоставляя преимуществ для перемещения вещей, вторые – прикладываемую силу. Подвижной блок перемещается с грузом, уменьшая прикладываемое для движения груза усилие.
Разберёмся, как найти выигрыш в силе в такой ситуации. Поднимая груз весом P посредством подвижного блока, нужно приложить вдвое меньшую силу, чем через неподвижный, ведь плечо OA (радиус) для силы P вдвое меньше OB (диаметра круга) для силы натяжения троса. Если тот вытягивается на длину l, груз поднимается только на половину этого расстояния l2:
Если тот вытягивается на длину l, груз поднимается только на половину этого расстояния l2:
С учётом силы трения формула расчета выигрыша в силе приобретает вид:
K – коэффициент трения.
Задача
Рабочий посредством подвижного блока поднимает ведро песка на высоту 6 м. При этом прилагается сила, равная 160 Н. Трение повышает прикладываемую силу на 10%. Рассчитать совершаемую человеком работу?
A = kFs=1,1*160*6= 1056 Дж 1,056 кДж.
Ответ: 1056 Дж
Какой выигрыш в силе даcт использование показанной на рисунке схемы?
Механизм представлен парой неподвижных и тремя подвижными блоками. Каждый снижает прикладываемую силу вдвое, даёт выигрыш в шесть раз.
Какой выигрыш в силе дает подвижный блок. Чем отличается подвижный блок от неподвижного? Золотое правило механики
Чаще всего простые механизмы используют, чтобы получить выигрыш в силе. То есть меньшей силой переместить больший по-сравнению с ней вес. При этом выигрыш в силе достигается не «бесплатно».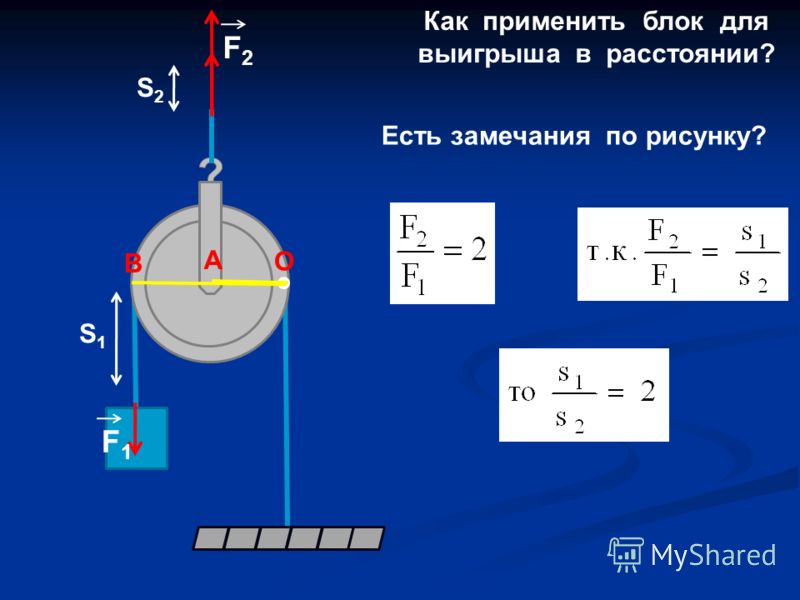 Расплатой за него является потеря в расстоянии, то есть требуется сделать большее перемещение, чем без использования простого механизма. Однако когда силы ограничены, то «обмен» расстояния на силу выгоден.
Расплатой за него является потеря в расстоянии, то есть требуется сделать большее перемещение, чем без использования простого механизма. Однако когда силы ограничены, то «обмен» расстояния на силу выгоден.
Подвижный и неподвижный блоки являются одними из видов простых механизмов. Кроме того, они являются видоизмененным рычагом, который также является простым механизмом.
Неподвижный блок не дает выигрыш в силе, он просто изменяет направление ее приложения. Представьте, что вам надо поднять за веревку тяжелый груз вверх. Вам придется тянуть его вверх. Но если использовать неподвижный блок, то тянуть надо будет вниз, в то время как груз будет подниматься вверх. В этом случае вам будет проще, так как необходимая сила будет складываться из силы мышц и вашего веса. Без использования неподвижного блока надо было бы прикладывать такую же силу, но она достигалась бы исключительно за счет силы мышц.
Неподвижный блок представляет собой колесо с желобом для веревки. Колесо закреплено, оно может вращаться вокруг своей оси, но не может перемещаться. Концы веревки (троса) свисают вниз, к одному прикреплен груз, а к другом прикладывается сила. Если тянуть за трос вниз, то груз поднимается вверх.
Концы веревки (троса) свисают вниз, к одному прикреплен груз, а к другом прикладывается сила. Если тянуть за трос вниз, то груз поднимается вверх.
Так как здесь нет выигрыша в силе, то нет и проигрыша в расстоянии. На какое расстояние поднимется груз, на такое же расстояние надо опустить веревку.
Использование подвижного блока дает выигрыш в силе в два раза (в идеале). Это значит, что если вес груза равен F, то чтобы его поднять, надо приложить силу F/2. Подвижный блок состоит всё из того же колеса с желобом для троса. Однако здесь закреплен один конец троса, а колесо подвижно. Колесо движется вместе с грузом.
Вес груза – это сила, направленная вниз. Его уравновешивают две силы, направленные вверх. Одну создает опора, к которой прикреплен трос, а другую тянущий за трос. Сила натяжения троса одинакова с обоих сторон, значит, между ними поровну распределяется вес груза. Поэтому каждая из сил в 2 раза меньше веса груза.
В реальных ситуациях выигрыш в силе меньше, чем в 2 раза, так как поднимающая сила частично «тратится» на вес веревки и блока, а также трение.
Подвижный блок, давая почти двойной выигрыш в силе, дает двойной проигрыш в расстоянии. Чтобы поднять груз на определенную высоту h, надо чтобы веревки с каждой стороны блока уменьшились на эту высоту, то есть в сумме получается 2h.
Обычно используют комбинации из неподвижных и подвижных блоков – полиспасты. Они позволяют получить выигрыш в силе и направлении. Чем больше в полиспасте подвижных блоков, тем больше будет выигрыш в силе.
Блок представляет собой устройство, имеющее форму колеса с желобом, по которому пропускают веревку, трос или цепь. Различают два основных вида блоков – подвижный и неподвижный. У неподвижного блока ось закреплена и при подъеме грузов не поднимается и не опускается (рис. 54), а у подвижного блока ось перемещается вместе с грузом (рис. 55).
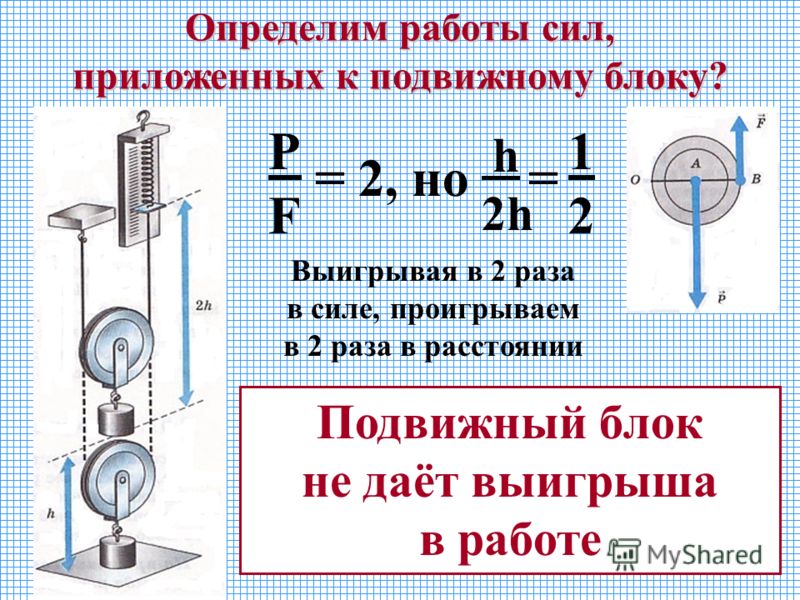
Неподвижный блок не дает выигрыша в силе. Его применяют для того, чтобы изменить направление действия силы. Так, например, прикладывая к веревке, перекинутой через такой блок, силу, направленную вниз, мы заставляем груз подниматься вверх (см.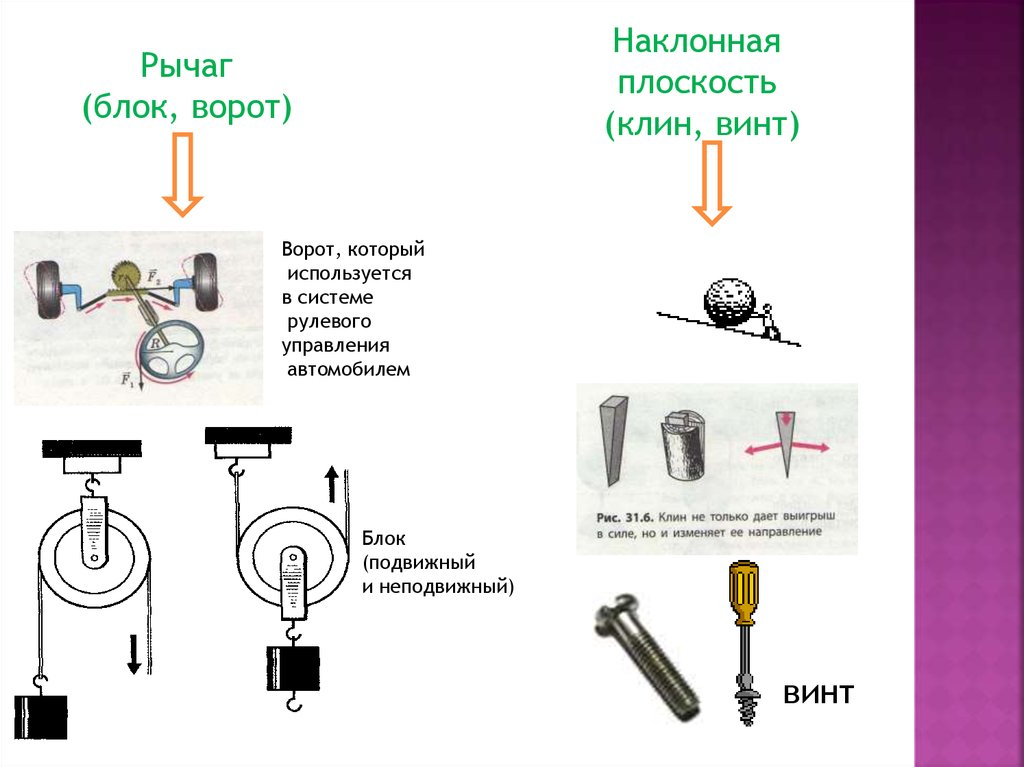 Рис. 54). Иначе обстоит дело с подвижным блоком. Этот блок позволяет небольшой силой уравновесить силу, в 2 раза большую. Для доказательства этого обратимся к рисунку 56. Прикладывая силу F
, мы стремимся повернуть блок вокруг оси, проходящей через точку О
. Момент этой силы равен произведению Fl
, где l
– плечо силы F
, равное диаметру блока ОВ
. Одновременно с этим прикрепленный к блоку груз своим весом Р
создает момент, равный, где – плечо силы Р
, равное радиусу блока ОА
. Согласно правилу моментов (21.2)
Рис. 54). Иначе обстоит дело с подвижным блоком. Этот блок позволяет небольшой силой уравновесить силу, в 2 раза большую. Для доказательства этого обратимся к рисунку 56. Прикладывая силу F
, мы стремимся повернуть блок вокруг оси, проходящей через точку О
. Момент этой силы равен произведению Fl
, где l
– плечо силы F
, равное диаметру блока ОВ
. Одновременно с этим прикрепленный к блоку груз своим весом Р
создает момент, равный, где – плечо силы Р
, равное радиусу блока ОА
. Согласно правилу моментов (21.2)
что и требовалось доказать.
Из формулы (22.2) следует, что P/F = 2. Это означает, что выигрыш, в силе, получаемый с помощью подвижного блока, равен 2 . Опыт, изображенный на рисунке 57, подтверждает этот вывод.
На практике часто применяют комбинацию подвижного блока с неподвижным (рис. 58). Это позволяет изменить направление силового воздействия с одновременным двукратным выигрышем в силе.
Для получения большего выигрыша в силе применяют грузоподъемный механизм, называемый полиспастом .
Полиспаст представляет собой комбинацию из двух обойм, одна из которых состоит из трех неподвижных блоков, а другая – из трех подвижных блоков (рис. 59). Поскольку каждый из подвижных блоков удваивает силу тяги, то в целом полиспаст дает шестикратный выигрыш в силе.
1. Какие два вида блоков вы знаете? 2. Чем отличается подвижный блок от неподвижного? 3. Для какой цели применяют неподвижный блок? 4. Для чего используют подвижный блок? 5. Что представляет собой полиспаст? Какой выигрыш в силе он дает?
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм – это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы – это рычаг и наклонная плоскость.
Рычаг.
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной оси.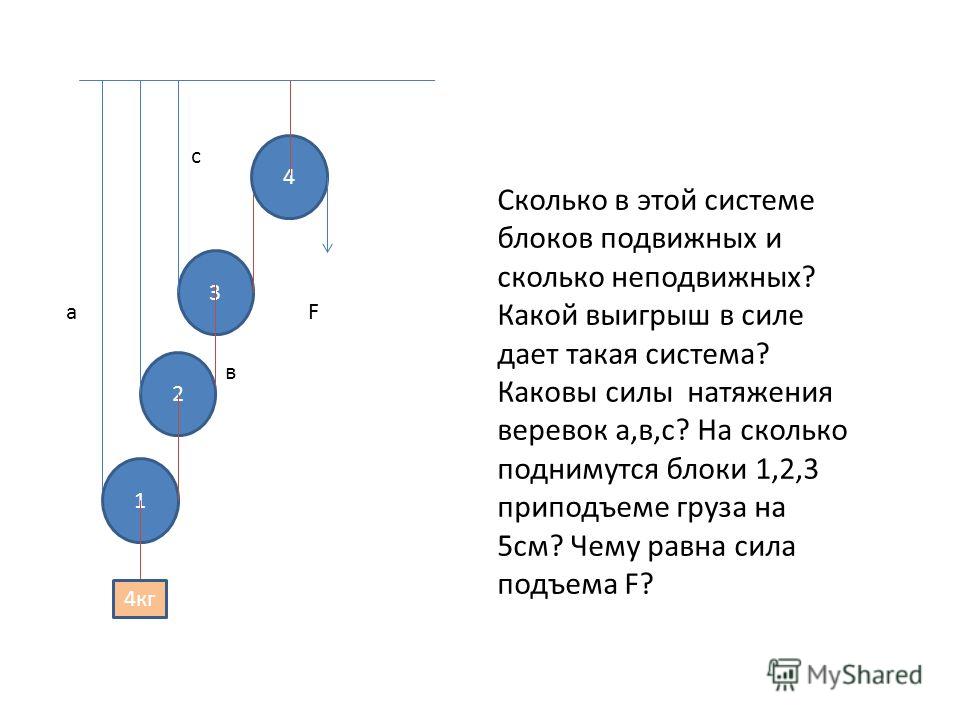 На рис. 1
) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и .
На рис. 1
) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и .
Условие равновесия рычага даётся правилом моментов: , откуда
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7: 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца – это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).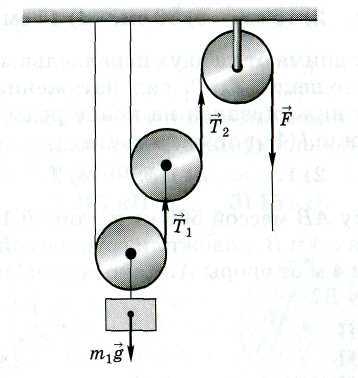
Неподвижный блок.
Важной разновидностью рычага является блок – укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
На правом конце нити в точке закреплён груз весом . Напомним, что вес тела – это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес прило жен к точке , в которой груз крепится к нити.
К левому концу нити в точке приложена сила .
Плечо силы равно , где – радиус блока. Плечо веса равно . Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство , а во-вторых, в процессе движении груза и нити перемещение точки равно перемещению груза.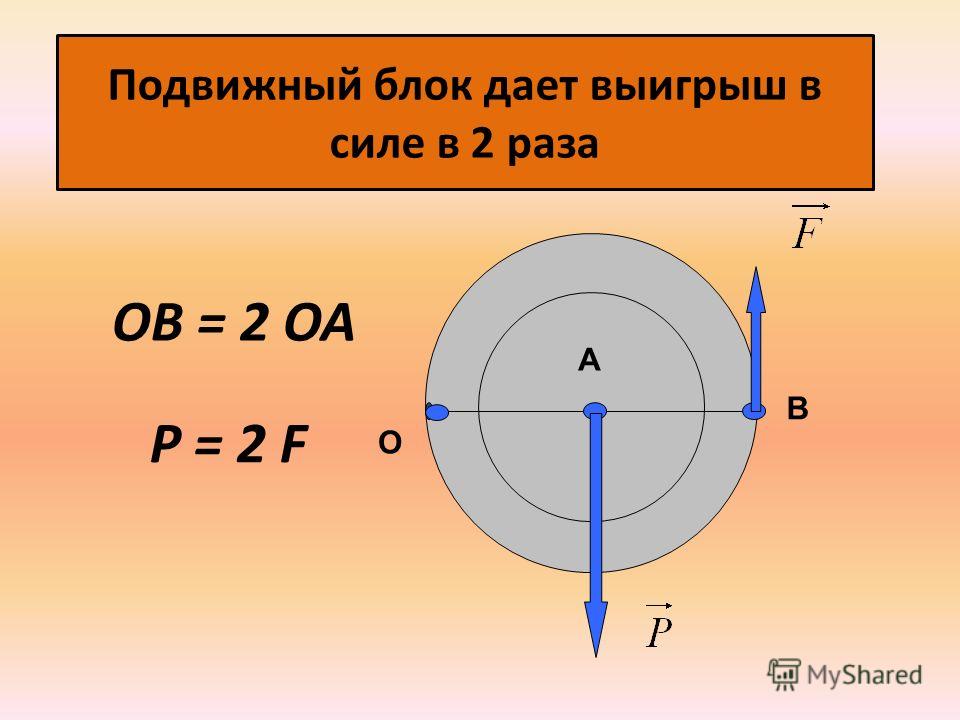
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Подвижный блок.
На рис. 3 изображён подвижный блок , ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити .
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы “перекатывается” через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке крепления груза к нити. Плечо силы равно .
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно . Соответственно, условием равновесия груза является равенство (что мы и видим на рис. 3
: вектор в два раза короче вектора ).
Соответственно, условием равновесия груза является равенство (что мы и видим на рис. 3
: вектор в два раза короче вектора ).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) – не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
На рис. 4
изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость – это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: “наклонная плоскость с углом “.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом . Эта сила , разумеется, направлена вдоль наклонной плоскости (рис. 5 ).
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
Проектируем на ось :
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что , поскольку . Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол .
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2: 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу . Но для поднятия груза на высоту большее плечо придётся опустить на , и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту над начальным положением, нам нужно пройти путь вдоль наклонной плоскости. При этом мы совершаем работу
т.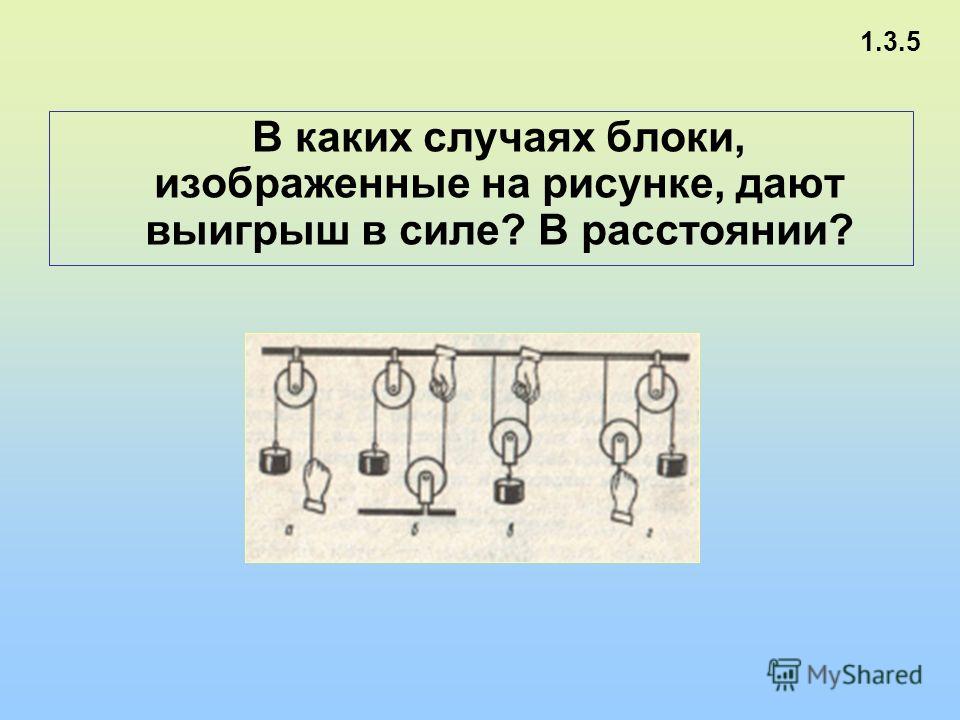 е. ту же самую, что и при вертикальном поднятии груза.
е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу A полн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=A полезн/А полн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен .
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы из точки в точку на высоту (рис. 6 ). В направлении, противоположном перемещению, на груз действует сила трения скольжения .
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
Тогда из (3) :
Подставляя это в (1) , получаем:
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
A полн=.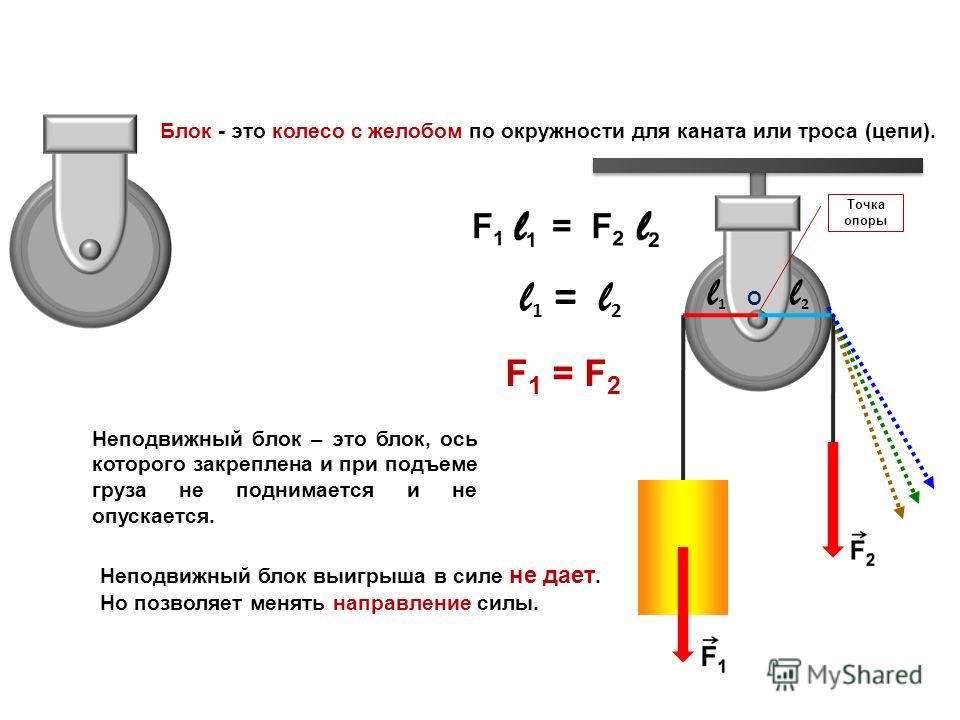
Полезная работа, очевидно, равна:
А полезн=.
Для искомого КПД получаем.
Команда «Физические пираты»
Исследовательское задание
Применяя систему блоков, получите выигрыш в силе в 2,3,4 раза. Какой выигрыш ещё получился? Представьте схемы соединения блоков и фото .
Цель: Применяя систему блоков, получить выигрыш в силе в 2,3,4 раза.
План:
Изучить, что такое блоки, для чего они нужны.
Провести эксперименты с блоками, получить выигрыш в силе в 2,3,4 раза.
Оформить работу.
Сделать фотоотчёт.
Отчёт:
Изучили, что неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе в 2 раза.
Выдвинули гипотезу :
Опыт№1. Получение выигрыша в силе в 2 раза с помощью подвижного блока .
Оборудование: штатив, 2 муфты, 1 лапка, стержень, 1 подвижный блок, 1 неподвижный блок, гиря массой 1 кг (весом 10 Н), динамометр, верёвка.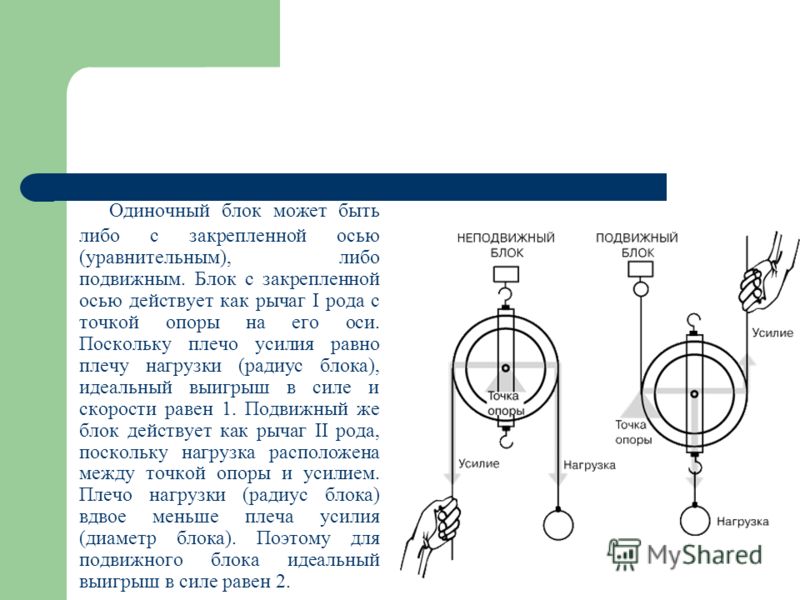
Проведение эксперимента:
1.На штативе закрепить неподвижный блок, стержень, так, чтобы плоскость неподвижного блока и конец стержня лежали в одной плоскости.
2. Один конец верёвки закрепить на стержне, верёвку перебросить через подвижный блок и через неподвижный блок.
3. К крючку подвижного блока подвесить гирю, к свободному концу верёвки прицепить динамометр.
5.Сделать вывод.
Результаты измерений:
Вывод: F = Р/2, выигрыш в силе в 2 раза.
Оборудование. Установка для опыта № 1.
Проведение опыта№1.
Опыт №2. Получение выигрыша в силе в 4 раза с помощью 2-х подвижных блоков.
Оборудование: штатив, 2 подвижных блока, 2 неподвижных блока, 2 гири массой 1 кг (весом 10 Н) каждая, динамометр, верёвка.
Проведение эксперимента:
1.На штативе с помощью 3 муфт и 2 лапок закрепить 2 неподвижных блока и стержень, так, чтобы плоскости блоков и конец стержня лежали в одной плоскости.
2. Один конец верёвки закрепить на стержне, верёвку перебросить последовательно через 1-й подвижный блок, 1-й неподвижный блок, 2-й подвижный блок, 2-й неподвижный блок.
3. К крючку каждого подвижного блока подвесить гирю, к свободному концу верёвки прицепить динамометр.
4. Измерить силу тяги (руки) динамометром, сравнить её с весом гирь.
5.Сделать вывод.
Установка для опыта №2.
Результаты измерений:
Вывод: F = Р/4, выигрыш в силе в 4 раза.
Опыт № 3. Получение выигрыша в силе в 3 раза с помощью 1-ого подвижного блока.
Для получения выигрыша в силе в 3 раза, надо использовать 1,5 подвижного блока. Так как нельзя отделить от подвижного блока половину, то следует использовать верёвку дважды: один раз перекинуть верёвку через него полностью, второй раз прицепить конец верёвки к его половине, т.е. к центру.
Оборудование: штатив, 1 подвижный блок с двумя крючками, 1 неподвижный блок, 1 гиря массой 1 кг (весом 10 Н), динамометр, верёвка.
Проведение эксперимента:
1.На штативе с помощью муфты закрепить 1 неподвижный блок.
2. Один конец верёвки прицепить к верхнему крючку подвижного блока, к нижнему крючку подвижного блока прицепить гирю.
3. Верёвку перекинуть последовательно от верхнего крючка подвижного блока через неподвижный блок, снова вокруг подвижного блока и снова через неподвижный блок, к свободному концу верёвки подцепить динамометр. Должно получиться 3 верёвки, на которые опирается подвижный блок – 2 по краям (полный блок) и одна к его центру (половина блока). Таким образом, мы используем 1,5 подвижного блока.
4. Измерить силу тяги (руки) динамометром, сравнить её с весом гири.
5.Сделать вывод.
Установка к опыту № 3. Проведение опыта№ 3.
Результаты измерений:
Вывод: F = Р/3, выигрыш в силе в 3 раза.
Вывод:
Проделав опыты №№1-3, мы проверили гипотезу, выдвинутую перед исследованием. Она подтвердилась. По результатам опытов, мы выяснили, следующие факты:
чтобы получить выигрыш в силе в 2 раза, нужно применить 1 подвижный блок;
чтобы выиграть в силе в 4 раза, надо применить 2 подвижных блока;
чтобы выиграть в 3 раза, надо применить 1,5 подвижных блока.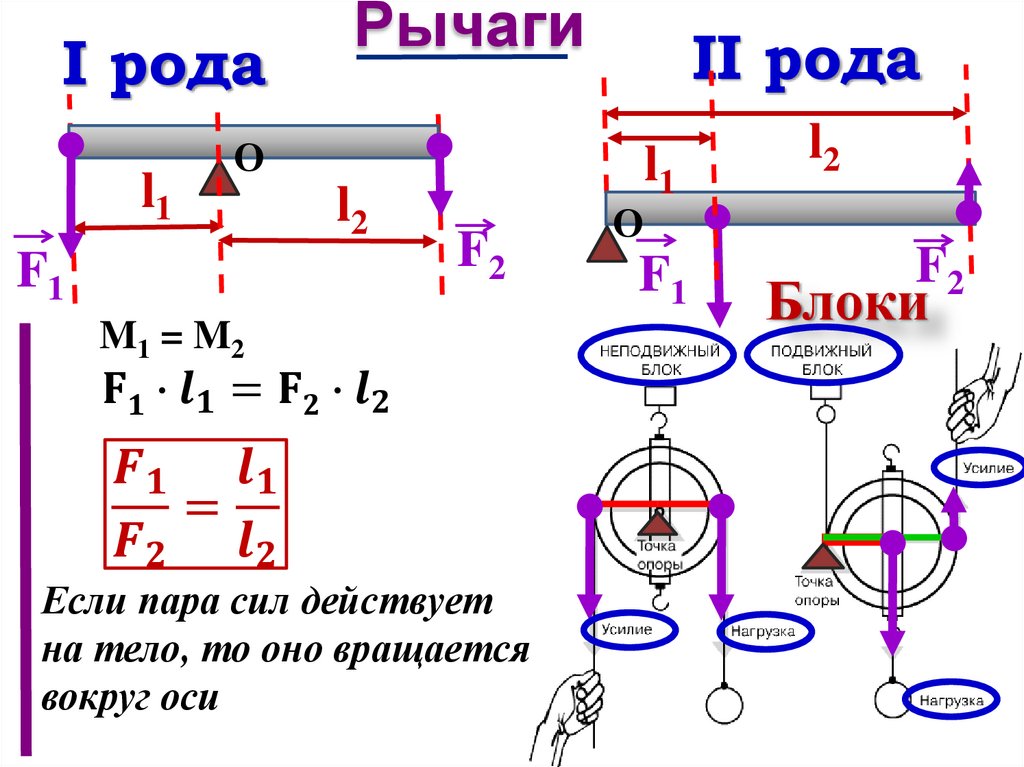
Также заметили, что выигрыш в силе равен числу верёвок, на которые опираются подвижные блоки:
в опыте №1: 1подвижный блок опирается на 2 верёвки – выигрыш в силе в 2 раза;
в опыте №2: 2 подвижных блока опираются на 4 верёвки – выигрыш в силе в 4 раза;
в опыте №3 подвижный блок опирается на 3 верёвки – выигрыш в силе в 3 раза.
Эту закономерность можно применять для получения любого числа выигрыша в силе. Например, для получения выигрыша в 8 раз надо применить 4 подвижных блока, чтобы они опирались на 8 верёвок.
Приложение:
Схемы блоков для опытов №№1-3.
См. на следующей странице.
Какой прирост силы дает подвижный блок. Чем подвижный блок отличается от неподвижного? Золотое правило механики
Чаще всего для набора прочности используют простые механизмы. То есть с меньшим усилием перемещать больший вес по сравнению с ним. При этом прирост мощности не достигается «бесплатно».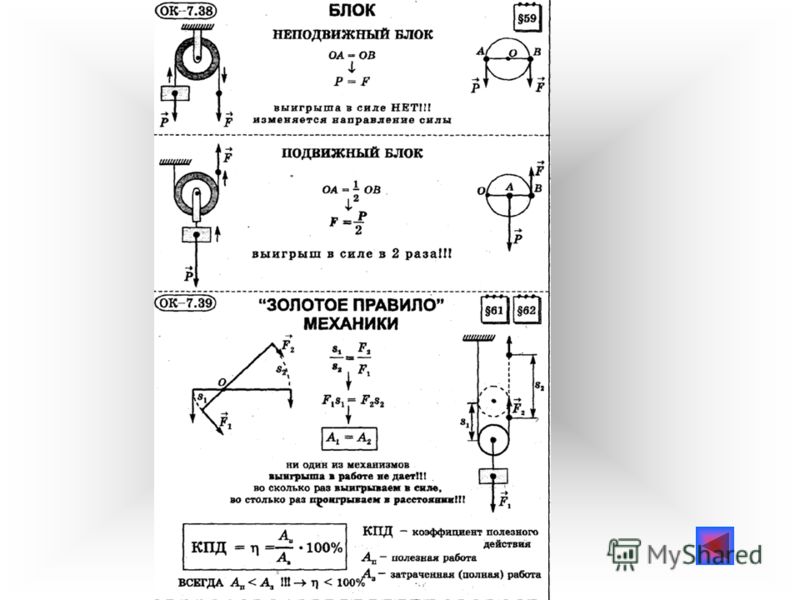 Цена за это – потеря в расстоянии, то есть требуется большее движение, чем без использования простого механизма. Однако, когда силы ограничены, выгоден «размен» расстояния на силу.
Цена за это – потеря в расстоянии, то есть требуется большее движение, чем без использования простого механизма. Однако, когда силы ограничены, выгоден «размен» расстояния на силу.
Подвижные и неподвижные блоки являются одними из типов простых механизмов. Кроме того, они представляют собой модифицированный рычаг, который также является простым механизмом.
Фиксированный блок не дает прибавки в силе, он просто меняет направление своего применения. Представьте, что вам нужно поднять за веревку тяжелый груз вверх. Вам придется его подтянуть. Но если использовать стационарный блок, то тянуть придется вниз, а груз будет подниматься вверх. В этом случае вам будет легче, так как необходимая сила будет складываться из силы мышц и вашего веса. Без использования неподвижного блока пришлось бы прикладывать такое же усилие, но оно достигалось бы исключительно за счет силы мышц.
Неподвижный блок представляет собой колесо с канатным желобом. Колесо неподвижно, оно может вращаться вокруг своей оси, но не может двигаться. Концы каната (троса) свисают вниз, к одному прикреплен груз, а к другому приложена сила. Если тянуть веревку вниз, груз поднимается вверх.
Концы каната (троса) свисают вниз, к одному прикреплен груз, а к другому приложена сила. Если тянуть веревку вниз, груз поднимается вверх.
Поскольку нет прироста силы, нет и потери в расстоянии. На какое расстояние будет подниматься груз, на такое же расстояние необходимо опустить веревку.
Применение прокатный блок дает прирост прочности в два раза (в идеале). Это означает, что если вес груза равен F, то для того, чтобы его поднять, необходимо приложить силу F/2. Подвижный блок состоит из того же колеса с тросовым желобком. Однако здесь один конец троса закреплен, а колесо подвижно. Колесо движется вместе с грузом.
Вес груза – это сила, направленная вниз. Он уравновешивается двумя восходящими силами. Один создается опорой, к которой крепится трос, а другой натягивается тросом. Тяговое усилие троса одинаково с обеих сторон, а значит, вес груза распределяется между ними поровну. Следовательно, каждая из сил в 2 раза меньше веса груза.
В реальных ситуациях выигрыш в силе менее чем в 2 раза, так как подъемная сила частично “тратится” на вес каната и блока, а также на трение.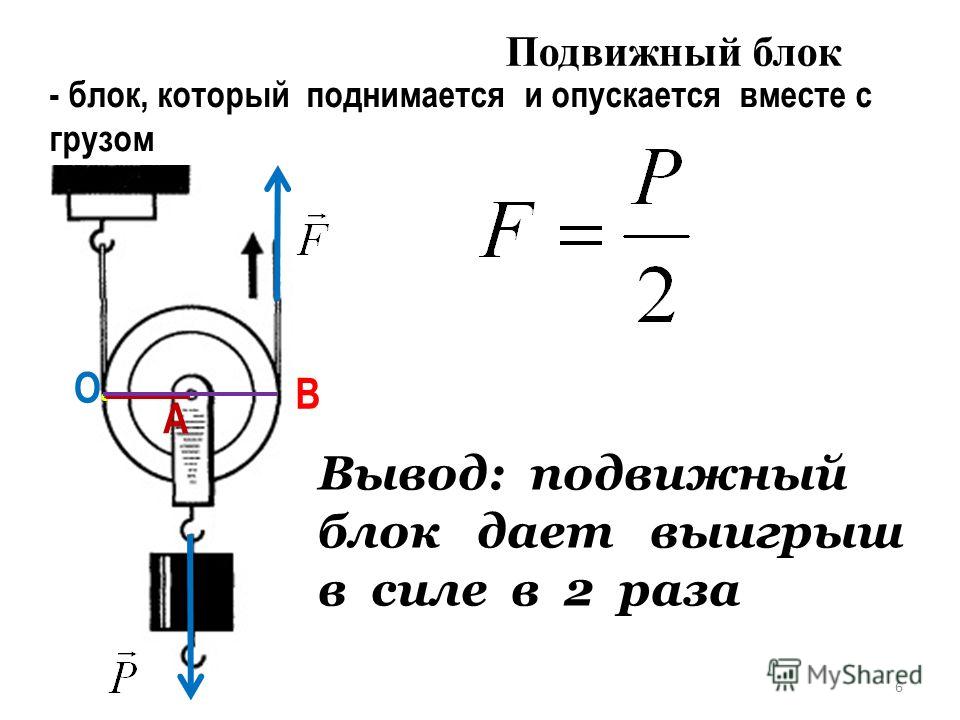
Подвижный блок, дающий почти двойной прирост силы, дает двойную потерю дистанции. Чтобы поднять груз на некоторую высоту h, необходимо, чтобы канаты с каждой стороны блока уменьшились на эту высоту, т. е. всего 2h.
Обычно используются комбинации неподвижных и подвижных блоков – полиспасты. Они позволяют увеличить силу и направление. Чем больше подвижных блоков в полиспасте, тем больше выигрыш в силе.
Блок представляет собой устройство в виде колеса с канавкой, через которую пропускают канат, трос или цепь. Блоки бывают двух основных типов — подвижные и неподвижные. У неподвижного блока ось неподвижна и при подъеме груза не поднимается и не опускается (рис. 54), а у подвижного блока ось перемещается вместе с грузом (рис. 55).
Неподвижный блок не дает прироста силы. Используется для изменения направления силы. Так, например, прикладывая к веревке, перекинутой через такой блок, направленную вниз силу, мы заставляем груз подниматься вверх (см. рис. 54). Иная ситуация с подвижным блоком. Этот блок позволяет небольшой силе уравновесить силу в 2 раза большую. Для доказательства обратимся к рис. 56. Приложив силу F, попытаемся повернуть брусок вокруг оси, проходящей через точку O. Момент этой силы равен произведению Fl, где l — плечо силы F , равный диаметру блока OB. При этом груз, прикрепленный к блоку своим весом Р, создает момент, равный, где плечо силы Р, равное радиусу блока ОА. По правилу моментов (21.2)
рис. 54). Иная ситуация с подвижным блоком. Этот блок позволяет небольшой силе уравновесить силу в 2 раза большую. Для доказательства обратимся к рис. 56. Приложив силу F, попытаемся повернуть брусок вокруг оси, проходящей через точку O. Момент этой силы равен произведению Fl, где l — плечо силы F , равный диаметру блока OB. При этом груз, прикрепленный к блоку своим весом Р, создает момент, равный, где плечо силы Р, равное радиусу блока ОА. По правилу моментов (21.2)
К.Э.Д.
Из формулы (22.2) следует, что P/F = 2. Это означает, что выигрыш в силе, полученный с подвижным агрегатом, равен 2 … Опыт, изображенный на рис. 57, подтверждает этот вывод.
На практике часто используется комбинация подвижного блока с неподвижным (рис. 58). Это позволяет изменять направление силового воздействия с одновременным двукратным выигрышем в силе.
Для получения большего прироста силы подъемный механизм под названием полиспаст … Греческое слово “полиспаст” образовано от двух корней: “поли” – много и “спао” – тяну, так что вообще получается “многотяг”.
Полиспаст представляет собой комбинацию двух зажимов, один из которых состоит из трех неподвижных блоков, а другой – из трех подвижных блоков (рис. 59). Поскольку каждый из движущихся блоков удваивает тяговое усилие, общий блок шкивов дает шестикратный выигрыш в силе.
1. Какие два типа блоков вы знаете? 2. Чем отличается подвижный блок от неподвижного? 3. Для какой цели используется неподвижный блок? 4. Для чего используется подвижный блок? 5. Что такое цепная таль? Какой прирост силы он дает?
Темы кодификатора ЕГЭ: простые механизмы, эффективность механизмов.
Механизм – устройство для преобразования усилия (увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.
Рычаг.
Рычаг представляет собой твердое тело, способное вращаться вокруг фиксированной оси. На рис. 1) показан рычаг с осью вращения. Силы и приложены к концам рычага (точкам и). Плечи этих сил равны соответственно и .
Плечи этих сил равны соответственно и .
Условие равновесия рычага задается правилом моментов:, откуда
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг дает выигрыш в силе или в расстоянии (в зависимости от цели, для которой он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы поднять вес 700 Н с усилием 100 Н, нужно взять рычаг с соотношением плеч 7:1 и разместить вес на коротком плече. Мы выиграем в 7 раз по силе, но столько же раз проиграем по дистанции: конец длинного плеча будет описывать в 7 раз большую дугу, чем конец короткого плеча (то есть вес).
Примеры рычагов, дающих преимущество в силе: лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, который дает вам расстояние. А обычные балочные весы представляют собой равноплечие рычаги, которые не выигрывают ни в расстоянии, ни в силе (иначе их можно использовать для взвешивания покупателей).
Фиксированный блок.
Важным типом кредитного плеча является блок – колесо, армированное в обойме с желобком, по которому пропускается канат. В большинстве задач веревка считается невесомой, нерастяжимой нитью.
На рис. 2 показан неподвижный блок, т.е. блок с фиксированной осью вращения (проходящей перпендикулярно плоскости рисунка через точку).
На правом конце нити в точке закреплен груз. Напомним, что вес тела – это сила, с которой тело давит на опору или растягивает подвес. В этом случае груз прикладывается к точке, в которой груз прикреплен к струне.
К левому концу нити в точке приложена сила.
Плечо силы равно, где – радиус блока. Плечо веса равно. Это означает, что неподвижный блок является равноплечим рычагом и поэтому не дает выигрыша ни в силе, ни в расстоянии: во-первых, мы имеем равенство, а во-вторых, в процессе движения груза и нити движение точка равна перемещению груза.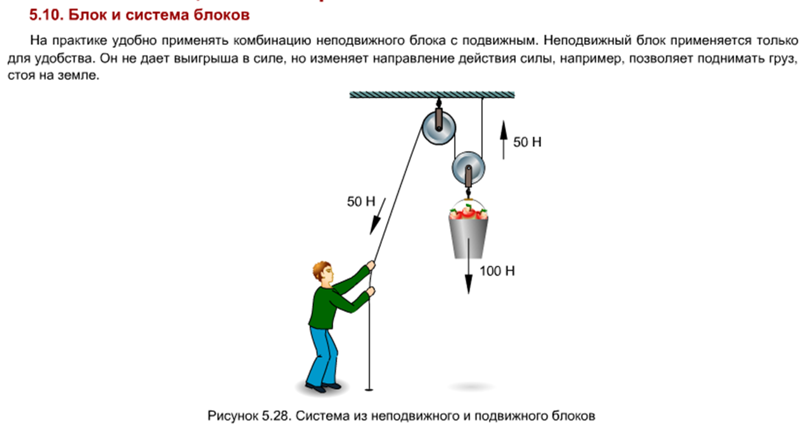
Зачем тогда вообще нужен фиксированный блок? Он полезен тем, что позволяет менять направление усилия. Обычно неподвижный блок используется в составе более сложных механизмов.
Подвижный блок.
На рис. 3 изображен подвижный блок , ось которого перемещается вместе с грузом. Тянем за нить с усилием, которое приложено в точке и направлено вверх. Блок вращается и одновременно также движется вверх, поднимая подвешенный на нити вес.
В данный момент времени неподвижной точкой является точка, и именно вокруг нее вращается блок (он «перекатывался» через точку). Еще говорят, что мгновенная ось вращения блока проходит через точку (эта ось направлена перпендикулярно плоскости чертежа).
Вес груза приложен в точке крепления груза к резьбе. Плечо силы равно.
Но плечо силы, с которой мы тянем нить, оказывается в два раза больше: оно равно. Соответственно, условием баланса нагрузки является равенство (что мы и видим на рис. 3: вектор короче вектора в два раза).
Соответственно, условием баланса нагрузки является равенство (что мы и видим на рис. 3: вектор короче вектора в два раза).
Следовательно, подвижный блок дает двукратный выигрыш в прочности. При этом, однако, мы дважды проигрываем в расстоянии: чтобы поднять груз на один метр, точку придется переместить на два метра (то есть вытянуть два метра нити).
Блок на рис. 3 имеет один недостаток: тянуть нить вверх (за острие) — не лучшая идея. Согласитесь, что гораздо удобнее тянуть нитку вниз! Здесь нам на помощь приходит фиксированный блок.
На рис. 4 показан подъемный механизм, представляющий собой комбинацию подвижного узла с неподвижным. К подвижному блоку подвешивается груз, а над неподвижным блоком дополнительно набрасывается трос, что дает возможность натянуть трос вниз для подъема груза вверх. Внешняя сила на кабеле снова обозначена вектором.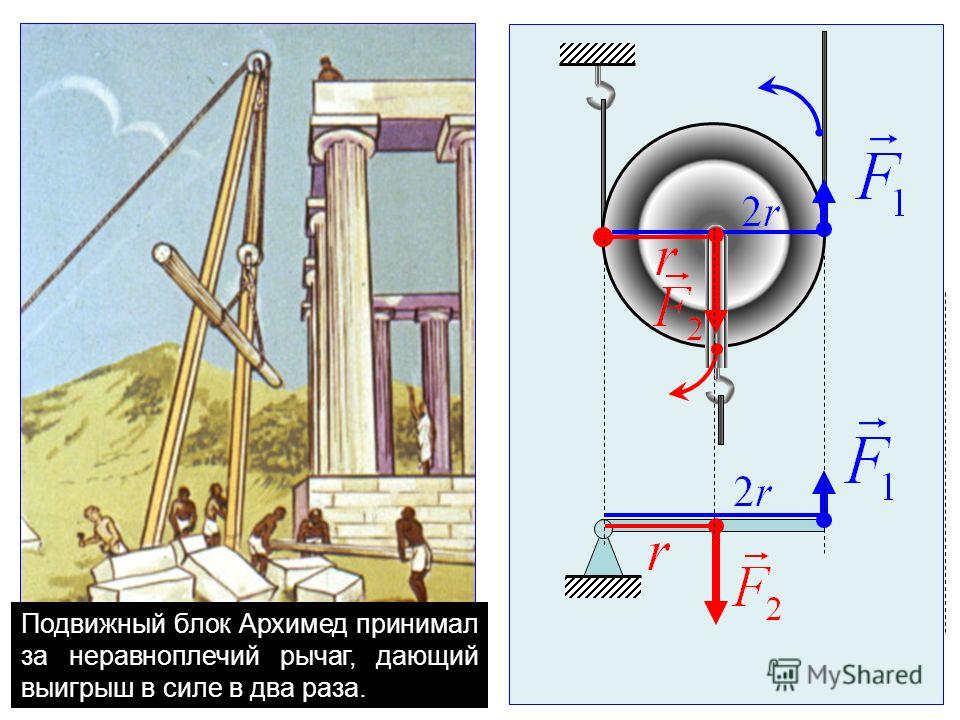
В принципе, это устройство ничем не отличается от движущегося агрегата: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как известно, тяжелую бочку легче перекатить по пандусу, чем поднять вертикально. Мосты, таким образом, представляют собой механизм, обеспечивающий увеличение прочности.
В механике такой механизм называется наклонной плоскостью. Наклонная плоскость представляет собой плоскую ровную поверхность, расположенную под углом к горизонту. В этом случае говорят кратко: «наклонная плоскость с углом».
Найдем силу, которую необходимо приложить к весу груза, чтобы равномерно поднять его по гладкой наклонной плоскости под углом. Эта сила, разумеется, направлена по наклонной плоскости (рис. 5).
| |
Выберем ось, как показано на рисунке.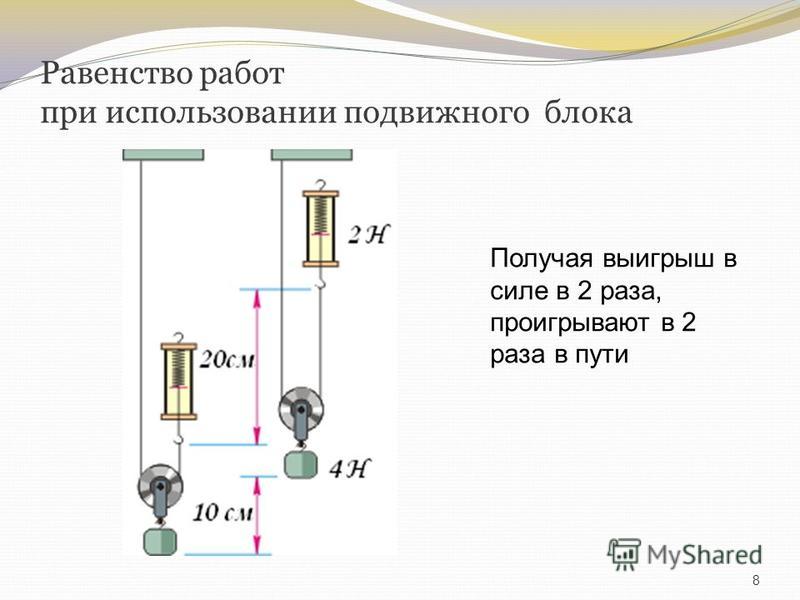 Так как груз движется без ускорения, то действующие на него силы уравновешены:
Так как груз движется без ускорения, то действующие на него силы уравновешены:
Проецируем на ось:
Это такая сила, которую необходимо приложить, чтобы переместить груз вверх по наклонной плоскости.
Чтобы равномерно поднять один и тот же груз по вертикали, нужно приложить силу, равную . Видно, что с. Наклонная плоскость действительно дает выигрыш в силе, причем тем больше, чем меньше угол.
Широко применяемыми разновидностями наклонной плоскости являются клиновая и винтовая.
Золотое правило механики.
Простой механизм может обеспечить увеличение силы или расстояния, но не может обеспечить увеличение производительности.
Например, рычаг с соотношением плеч 2:1 удваивает силу. Чтобы поднять груз с весом на меньшем плече, нужно приложить силу к большему плечу. Но чтобы поднять груз на высоту, большее плечо придется опустить на , и проделанная работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае с наклонной плоскостью мы выигрываем в силе, так как прикладываем к грузу силу, меньшую силы тяжести. Однако для того, чтобы поднять груз на высоту выше исходного положения, нам нужно пройти путь по наклонной плоскости. При этом делаем работу
то есть то же, что и для вертикального подъема груза.
Эти факты являются проявлением так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не дает выигрыша в производительности. Сколько раз мы выигрываем в силе, сколько раз проигрываем в расстоянии, и наоборот.
Золотое правило механики — не что иное, как упрощенная версия закона сохранения энергии.
Эффективность механизма.
На практике следует различать полезную работу A полезную для выполнения механизмом в идеальных условиях без каких-либо потерь и полную работу A полную,
которая выполняется для тех же целей в реальной ситуации .
Полная работа равна сумме:
– полезная работа;
– работа, выполняемая против сил трения в различных частях механизма;
– работа, совершаемая по перемещению составных частей механизма.
Так, при подъеме груза рычагом, кроме того, необходимо совершить работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего определенный вес.
Полная работа всегда приносит больше удовольствия. Отношение полезной работы к полной называется КПД механизма:
= А полезного / А полного
КПД обычно выражается в процентах. КПД реальных механизмов всегда меньше 100%.
Рассчитаем КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен.
Пусть вес массы поднимается равномерно по наклонной плоскости под действием силы от точки к точке на высоту (рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения.
| |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
Проецируем на ось X:
. (1)
(1)
Проецируем по оси Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
Тогда из (3):
Подставляя это в (1), получаем:
Полная работа равна произведению силы F на путь, пройденный телом по поверхности наклонной плоскости:
А полный =.
Полезная работа, очевидно, равна:
A полезная =.
Для нужной эффективности получаем.
Команда “Физические пираты”
Исследовательское задание
Используя систему блоков, вы получите в 2,3,4 раза больше силы. Что еще ты выиграл? Прислать схемы подключения блоков и фото .
Цель: Используя блочную систему, получить прирост силы в 2,3,4 раза.
План:
Узнайте, что такое блоки и для чего они нужны.
Проведите эксперименты с блоками, получите прирост прочности в 2,3,4 раза.
Проверить работу.
Сделать фотоотчет.
Отчет:
Мы узнали, что неподвижный блок не дает прибавки в силе, а подвижный блок дает прибавку в силе в 2 раза.
Выдвинуть гипотезу :
Опыт №1. Получение прибавки прочности в 2 раза с помощью прокатного блока .
Оборудование: штатив, 2 муфты, 1 ножка, стержень, 1 подвижный блок, 1 неподвижный блок, груз 1 кг (10 Н), динамометр, веревка.
Эксперимент:
1. На штативе закрепить стационарный блок, стержень так, чтобы плоскости стационарного блока и конца стержня лежали в одной плоскости.
2. Закрепите один конец веревки на стержне, перекиньте веревку через подвижный блок и через неподвижный блок.
3. Подвесьте груз на крюк подвижного блока, к свободному концу веревки прикрепите динамометр.
5. Сделать вывод.
Результаты измерений:
Вывод: F= P/2, выигрыш в силе в 2 раза.
Оборудование. Установка для опыта №1.
Опыт №1.
Опыт №2. Получение прибавки в силе в 4 раза с помощью 2-х подвижных блоков.
Оборудование: штатив, 2 подвижных блока, 2 неподвижных блока, 2 груза массой 1 кг (массой 10 Н) каждый, динамометр, веревка.
Эксперимент:
1. На штативе с помощью 3-х муфт и 2-х ножек закрепить 2 неподвижных блока и стержень так, чтобы плоскости блоков и конец стержня лежали в одной плоскости.
2. Закрепить один конец веревки на удилище, перекинуть веревку последовательно через 1-й подвижный блок, 1-й неподвижный блок, 2-й подвижный блок, 2-й неподвижный блок.
3. Подвесьте груз к крюку каждого подвижного блока, к свободному концу веревки прикрепите динамометр.
4. Измерить силу тяги (руки) динамометром, сравнить с весом гирь.
5. Сделать вывод.
Установка для эксперимента №2.
Результаты измерений:
Вывод: F= P/4, прирост силы в 4 раза.
Опыт №3. Получение прибавки в силе в 3 раза с помощью 1-го подвижного блока.
Чтобы получить прирост силы в 3 раза, нужно использовать 1,5 подвижных блока. Так как половинку от подвижного блока отделить невозможно, следует использовать веревку дважды: один раз перекинуть веревку полностью через него, второй раз привязать конец веревки к его половинке, т. е. к центру.
е. к центру.
Оборудование: штатив, 1 подвижный блок с двумя крючками, 1 неподвижный блок, 1 груз 1 кг (10 Н), динамометр, веревка.
Эксперимент:
1.На штативе с помощью муфты закрепить 1 стационарный блок.
2. Прикрепите один конец веревки к верхнему крюку подвижного блока, к нижнему крюку подвижного блока прикрепите груз.
3. Перебросить веревку последовательно с верхнего крюка подвижного блока через неподвижный блок, снова вокруг подвижного блока и снова через неподвижный блок, чтобы подобрать динамометр к свободному концу веревки. У вас должно получиться 3 веревки, на которых держится подвижный блок — 2 по краям (полный блок) и одна ближе к его центру (половина блока). Таким образом, мы используем 1,5 движущихся блока.
4. Измерьте силу тяги (руки) динамометром, сравните с весом гири.
5. Сделать вывод.
Установка для опыта №3. Проведение опыта №3.
Результаты измерений:
Вывод: F= P/3, прирост силы в 3 раза.
Вывод:
Проведя опыты №1-3, мы проверили выдвинутую перед исследованием гипотезу. Она подтвердилась. По результатам экспериментов мы выяснили следующие факты:
чтобы получить прирост силы в 2 раза, нужно использовать 1 подвижный блок;
чтобы победить в силе 4 раза, нужно использовать 2 подвижных блока;
чтобы выиграть 3 раза, нужно использовать 1,5 подвижных блока.
Мы также заметили, что выигрыш в силе равен количеству канатов, на которых опираются подвижные блоки:
в опыте №1: 1 подвижный блок опирается на 2 веревки – увеличение силы в 2 раз;
в эксперименте №2: 2 подвижных блока на основе 4 веревки – увеличение силы в 4 раз;
в эксперименте №3 подвижный блок основан на 3 веревки – увеличение силы в 3 раз.
Этот шаблон можно применять для получения любого количества прироста силы. Например, чтобы получить выигрыш в 8 раз, нужно использовать 4 подвижных блока так, чтобы они опирались на 8 веревок.
Заявка:
Блок-схемы для опытов №1-3.
См. следующую страницу.
Механическое преимущество Block & Tackle
Обновлено 24 апреля 2017 г.
Автор: David Weinberg
Блоки и полиспасты — это машина, которая значительно снижает величину силы, необходимой для перемещения или подъема объекта, например тяжелого ящика. . Стандартный шкив состоит из одного колеса на оси, по которому проходит канат. Сам по себе шкив может изменить только направление силы, приложенной к объекту. Система блоков, работающих вместе, может образовывать блок и захват, который умножает силу в дополнение к изменению направления силы, что означает, что для перемещения объекта требуется меньшее усилие. Степень, в которой блок и снасть умножают силу, является их механическим преимуществом.
Функция
Блоки и тали часто используются в местах, где тяжелая техника недоступна и вместо нее необходимо использовать человеческую силу. В древности блоки и тали использовались в строительных проектах для перемещения тяжелых грузов. В современную эпоху они часто используются на лодках, где было бы нецелесообразно иметь кран или другое тяжелое подъемное оборудование.
В древности блоки и тали использовались в строительных проектах для перемещения тяжелых грузов. В современную эпоху они часто используются на лодках, где было бы нецелесообразно иметь кран или другое тяжелое подъемное оборудование.
Подъем с помощью шкива
Если бы мы пытались поднять ящик весом 200 фунтов с пола на стропила здания, мы могли бы сделать это с помощью простого шкива. Мы помещали один блок в стропила и пропускали через него веревку, прикрепляя один конец веревки к обрешетке. Потянув за другой конец веревки (тяговую часть), мы смогли поднять ящик на стропила. В этой системе каждый раз, когда мы тянем веревку на один фут с усилием в 200 фунтов. силы, мы поднимаем ящик на одну ногу. Подъем чего-либо менее 200 фунтов. силы не сдвинет наш 200-фунтовый ящик.
Подъем с помощью блока и талей
Если вместо того, чтобы прикреплять веревку непосредственно к обрешетке, мы пропускаем ее через новый шкив, прикрепленный к обрешетке, а затем прикрепляем конец веревки к стропилам, у нас будет блок и снасть. Теперь каждый раз, когда мы тянули за свободный конец веревки, веревке приходилось проходить между стропилами и обрешеткой дважды. Нам пришлось бы тянуть два фута за веревку, чтобы поднять ящик на один фут. Однако нам пришлось бы тянуть только 100 фунтов. силы.
Теперь каждый раз, когда мы тянули за свободный конец веревки, веревке приходилось проходить между стропилами и обрешеткой дважды. Нам пришлось бы тянуть два фута за веревку, чтобы поднять ящик на один фут. Однако нам пришлось бы тянуть только 100 фунтов. силы.
Механическое преимущество
Это несоответствие между силой, необходимой для перемещения объекта, и весом объекта является механическим преимуществом блока и снасти. Это то же самое, что и несоответствие между тем, сколько веревки мы тянем, и расстоянием, которое перемещает объект. Чтобы вычислить механическое преимущество, мы можем либо разделить вес поднимаемого объекта на силу, необходимую для его подъема, либо разделить количество веревки, которую мы должны тянуть, на расстояние, на которое перемещается объект. Чтобы найти механическое преимущество нашей машины с помощью первого метода, мы должны разделить вес ящика, 200 фунтов, на величину силы, необходимой для его подъема, 100 фунтов, что даст нам механическое преимущество, равное двум. Разделив количество веревки, которую мы тянем за раз, 2 фута, на расстояние, на которое поднимается ящик, 1 фут, мы получим тот же ответ. Как правило, количество отрезков каната между двумя шкивами в блоке и полиспасте соответствует механическому преимуществу машины. В нашей машине веревка проходит от верхнего шкива к нижнему шкиву и обратно к стропилам: две длины веревки дают нам механическое преимущество над двумя.
Разделив количество веревки, которую мы тянем за раз, 2 фута, на расстояние, на которое поднимается ящик, 1 фут, мы получим тот же ответ. Как правило, количество отрезков каната между двумя шкивами в блоке и полиспасте соответствует механическому преимуществу машины. В нашей машине веревка проходит от верхнего шкива к нижнему шкиву и обратно к стропилам: две длины веревки дают нам механическое преимущество над двумя.
Сила и работа
Несмотря на то, что блок и захват уменьшают количество силы, необходимой для перемещения объекта, это не меняет количество работы. Например, блок и снасть с механическим преимуществом в четыре раза позволят вам поднять объект весом 4 фунта с усилием всего в 1 фунт. Однако вам также потребуется тянуть 4 фута веревки, чтобы поднять объект на один фут.
Трение
Когда какой-либо объект движется против другого объекта, часть энергии движущегося объекта теряется из-за трения. В блоке и захвате некоторое трение в шкивах уменьшит механическое преимущество машины.