Кинематическая схема привода: 1. Кинематическая схема привода

1. Кинематическая схема привода

двигатель клиноременная передача цилиндрический редуктор упругая муфта с торообразной оболочкой ведущая звездочка конвейера тяговая цепь	Исходные данные: Тяговая сила цепи Скорость тяговой цепи Шаг тяговой цепи Число зубьев звездочки Срок службы привода лет
Валы: В1 – двигателя, В2 – быстроходный редуктора, В3. тихоходный редуктора, В4 – рабочей машины (тяговой цепи)

2.

Выбор электродвигателя. Кинематический и силовой расчет привода

2.1. Определение номинальной мощности и номинальной частоты вращения двигателя

Мощность двигателя зависит от требуемой мощности рабочей машины, а его частота вращения – от частоты вращения приводного вала рабочей машины.

Исходные данные:

– тяговая сила цепи конвейера,

– скорость цепи конвейера.

1. Определяем требуемую мощность конвейера:

2. Определяем КПД привода:

где – КПД закрытой передачи (цилиндрический редуктор),

– КПД открытой передачи (клиноременная передача),

– КПД муфты,

– КПД подшипников качения (по кинематической схеме в редукторе две пары подшипников),

– КПД подшипников скольжения (по схеме на приводном валу конвейера одна пара подшипников).

3. Находим требуемую мощность двигателя:

.

Из условия потаблице диапазонов мощностей трехфазных асинхронных двигателей серии 4А (А.Е. Шейнблит «Курсовое проектирование деталей машин», таблица 2.1, стр.41) выбираем ближайшее к требуемой мощности двигателя значение номинальной мощности.

4. По значению номинальной мощности выбираем четыре варианта типа двигателя серии А4:

Вариант	Тип двигателя	Номинальная мощность	Частота вращения, об/мин
			синхронная	При номинальном режиме
1	4АМ112МАУ3	2,2	750	700
2	4АМ100L6У3	2,2	1000	950
3	4АМ90L4У3	2,2	1500	1425
4	4АМ80В2У3	2,2	3000	2850

2.

2. Определение передаточного числа привода

Исходные данные:

– скорость тяговой цепи конвейера,

– число зубьев звездочки,

– шаг тяговой цепи.

1. Определяем частоту вращения приводного вала конвейера:

– диаметр барабана,

.

2. Находим передаточное число привода для каждого варианта: ,

,,,.

3. Передаточное число привода .

Рекомендуемые значения передаточных чисел для открытой ременной и закрытой цилиндрической зубчатой передач соответственно:

,.

Следовательно, передаточное число привода .

В этот промежуток попадают передаточные числа для первого и второго вариантов двигателя. Из двух вариантов выбираем второй (,), так как первый вариант (;) не рекомендуется для приводов общего назначения.

Выбрали двигатель 4АМ100L6У3

4. Производим разбивку передаточного числа привода: ,

2.3. Кинематический и силовой расчет привода

Индексом Б обозначены параметры быстроходного вала, Т – тихоходного, дв – двигателя, вых – конвейера.

1. Кинематические характеристики:

Частоты вращения:

,

,

,

.

Угловые скорости:

,

,

,

.

2. Силовые характеристики:

Мощности:

,

,

,

.

Вращающие моменты:

,

,

,

.

Тип двигателя 4АМ100L6 У3 ;
Параметр	Передача		Параметр	Вал
	закрытая цилиндр. зубчатая	открытая ременная		двигателя	редуктора		тяговой цепи
					быстроходный	тихоходный
Передаточное число	5,0	3,68	Расчетная мощность Р, кВт	1,69	1,64	1,59	1,54
			Угловая скорость	99,48	27,03	5,41	5,41
КПД	0,97	0,97	Частота вращения п, об/мин	950	258,15	51,63	51,63
			Вращающий момент Т,	16,98	60,91	293,96	285,2

Кинематическая схема привода технологической машины.

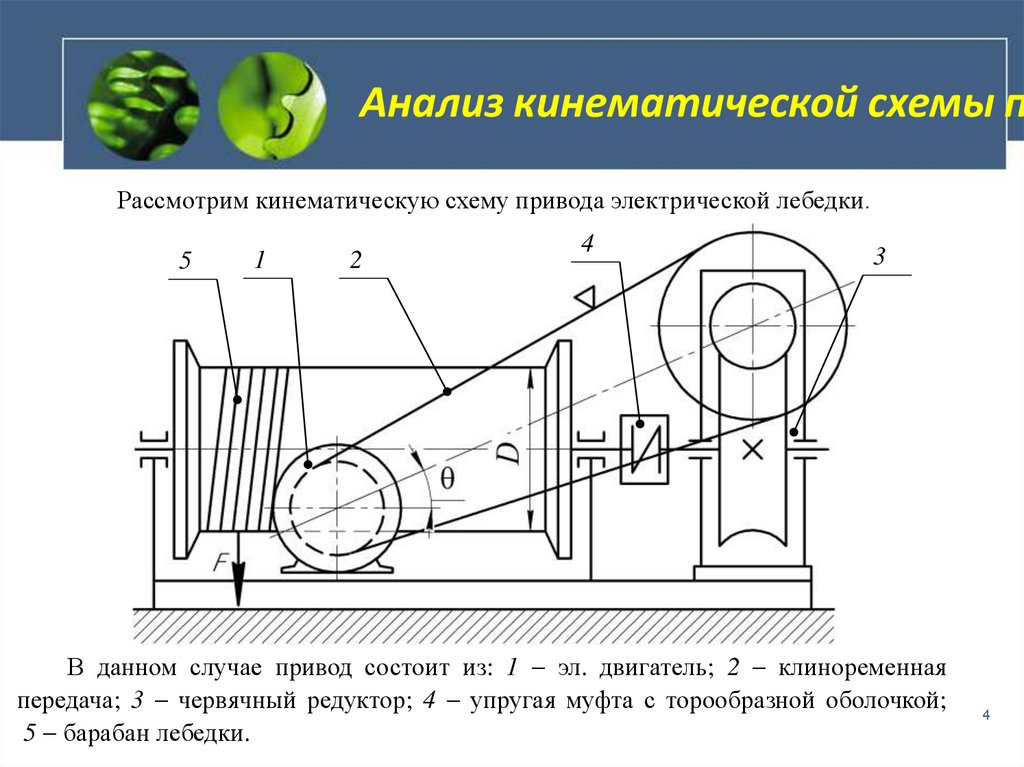Обозначения элементов привода на кинематических схемах

Похожие презентации:

Грузоподъемные машины. (Лекция 4.1.2)

Зубчатые передачи

Гидравлический домкрат в быту

Детали машин и основы конструирования

Газораспределительный механизм

Свайные фундаменты. Классификация. (Лекция 6)

Ременные передачи

Редукторы

Техническая механика. Червячные передачи

Фрезерные станки. (Тема 6)

1. Прикладная механика

Давидович
Игорь Юрьевич
(курс лекций)
Кинематическая схема привода
технологической машины.
Обозначения элементов привода
на кинематических схемах.
к. 205, корпус 1, т. 80222410512
E-mail: [email protected]
1

2. Источник движения

м
2

3. Передача гибкой связью (клиноременная)

3

4. Передача зацеплением (цепная)

x
x
4

5. Передача зацеплением (зубчатая цилиндрическая)

x
x
5

6. Передача зацеплением (зубчатая коническая)

6

7.

Передача зацеплением (червячная) 7
МУФТЫ
жесткая
упругая
8
Цилиндрический редуктор
ЦР
9
Конический редуктор
КР
10
Коническо-цилиндрический
редуктор
КЦР
11
Червячный редуктор
ЧР
12
Рабочие органы машин
Цепной транспортер
x
x
x
x
Обозначение на кинематической схеме
13
Рабочие органы машин
Ленточный транспортер
Обозначение на кинематической схеме
14
Рабочие органы машин
Винтовой (шнековый) транспортер
а – горизонтальный транспортер
б – вертикальный транспортер
Обозначение на кинематической схеме
15
Рабочие органы машин
Грузоподъемное устройство (таль)
m
Обозначение на кинематической схеме
16
Кинематическая схема привода
м
ЧР
Составить кинематическую схему для
привода, состоящего из электродвигателя,
упругой муфты и червячного редуктора
17
Кинематическая схема привода
Х
м
Составить кинематическую схему
для привода, состоящего из двигателя,
упругой муфты, цилиндрического
редуктора, цепной передачи и
приводного вала цепного транспортера
x
x
x
x
ЦР
Х
18
Кинематическая схема привода
М
ЦР
x
Привод, состоящий из двигателя,
упругой муфты, цилиндрического
редуктора и цепной передачи
x
19
Кинематическая схема привода
М
ЦР
X
X
Привод, состоящий из электродвигателя,
упругой муфты, цилиндрического
редуктора и клиноременной передачи
20
Кинематическая схема привода
Задание:
Составить кинематическую схему привода ленточного транспортера,
состоящего из электродвигателя, упругой муфты, коническоцилиндрического редуктора и клиноременной передачи
X
X
М
КЦР
21
Кинематическая схема привода
Задание:
ЧР
x
Составить кинематическую
схему привода барабана
лебедки, состоящего из:
электродвигателя
упругой муфты
червячного редуктора
цепной передачи
М
x
m
22

English     Русский Правила

Читать журналы GJRE

(Пожалуйста, подождите, показ может занять несколько секунд)

• Опубликуйте у нас видео

  Если картинка стоит тысячи слов, то видео стоит миллиона. Транслируйте свои исследования в видеоформате бесплатно.

  Узнайте больше и отправьте свое видео

• Организуйте конференцию вместе с нами

  Давайте делать по-крупному. Организуйте, сотрудничайте и спонсируйте предстоящие семинары, семинары, симпозиумы, конференции и вебинары.

  Связаться с Evangelist

• Доступ к инфраструктуре научного сообщества

  • Используйте нашу стандартную облачную инфраструктуру для проведения исследований.
  • Получите доступ к соответствующим спонсорам исследовательского проекта.
  • Автоматизированные инструменты позволяют нам сотрудничать и проверять вашу рукопись и ссылки во время процесса создания в облаке.

  Отправьте свой проект

• Резервуар знаний диссертаций и электронных книг

  Опубликуйте у нас свою электронную книгу, диссертацию или диссертацию. Наша служба публикации электронных книг с открытым доступом позволяет авторам совместно с нами редактировать рукопись.

  Подать диссертацию Подать электронную книгу

• Подписаться на журналы

Блог о социальных инновациях

• Поиск глобальных журналов «Жизненной энергии» планет | Блог о социальных инновациях и историях

  Обзор моей последней статьи и доступ к блогу в Google Cloud Автор: Джон Ф. Кэдди, доктор философии. продуктивность в прошлом[…]

  Подробнее…

• Краткий обзор «Исследование осуществимости теорий художественного перевода Сюй Юаньчуна и его открытий»

  Global Journals | Блог о социальных инновациях и историях

  Автор: Fangfang Tan ＊ Шанхайский педагогический университет, КНР Эта статья состоит из пяти частей. Первая часть служит введением к блестящим достижениям профессора Сюй в области перевода. Он известен как первый человек, переведший классический китайский[…]

  Подробнее. ..

• Разум и будущее национального государства

  Глобальные журналы | Блог социальных инноваций и историй

  Блог. Хосе Луис Техеда Гонсалес. Статья, опубликованная в Global Journal под названием «Разум и будущее национального государства», была сделана в рамках расширения глобализации и кризиса национальных государств. Все говорило бы о том, что регионализация и[…]

  Подробнее…

• «Пустые пространства» в структуре современных культурных ландшафтов: идентификация ради социально-экономической стабильности

  Глобальные журналы | Блог о социальных инновациях и историях

  Автор: Т.М. КрасовскаяЭто мой первый опыт публикаций в Global Journals. Это оказалось успешным. Доволен контактами с редакцией и техническими отделами. Это тоже мой первый опыт блогерской деятельности – №[…]

  Подробнее…

• Родственные корни моего интереса к изучению критических ситуаций и участие в них волонтера

  Глобальные журналы | Блог о социальных инновациях и историях

  Автор: проф. Олег ЯницкийКонечно, это некоторое преувеличение, но тем не менее это так. Так уж получилось, что мое детство совпало с длинной чередой удушающих событий и радикальных преобразований в России. Основным был Второй мировой война, и […]

  Читать подробности …

Представление

Глобальные журналы Ebooks

и тезис

Служба публикации

Начало

2

. ГЖСС-Г

Системные требования LMS с точки зрения библиотек

Библиотечные услуги необходимы для обучения. Поэтому концепция редизайна LMS должна гарантировать лучшую интеграцию библиотечных услуг, таких как каталоги, базы данных и медиа, а также управление литературой и информацией. Сравнение с другими отраслями может быть полезным: часто отношения с клиентами поддерживаются и укрепляются с помощью учетных записей клиентов.0003

Франция имеет очень уважаемую систему образования с тремя основными уровнями: начальное, среднее и высшее образование.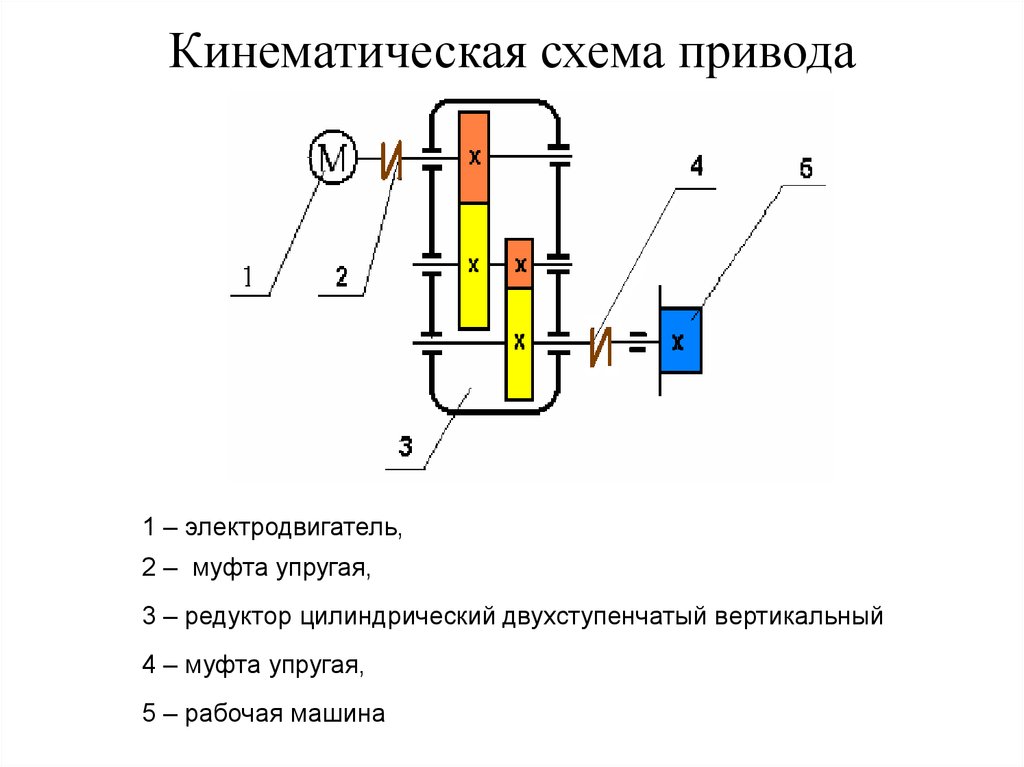 Начальное и среднее образование являются обязательными и бесплатными, а высшее образование делится на государственные и частные учебные заведения. Французское правительство играет центральную роль в политике и финансировании образования, при этом большая часть финансирования направляется на…

Read Paper

Публикации в прессе

 

Расизм в Бразилии: государственная автономия смягчения социального неравенства

Цель этой статьи — обсудить права человека выходцев из Африки и их эволюцию в Бразилии, особенно в отношении исторической, политической и социальной структуры. Анализируется характеристика информации от колониального периода до современной Бразилии, при этом рассматриваются противопоставление расизма и прав завоевания…

Повествование об следственном процессе. Первое испытание веры Паулы де Эгилуз (Картахена-де-Индиас, 1623–1626 гг.)

В 1624 году был начат процесс против Паулы де Эгилуз, черной рабыни, обвиненной в колдовстве.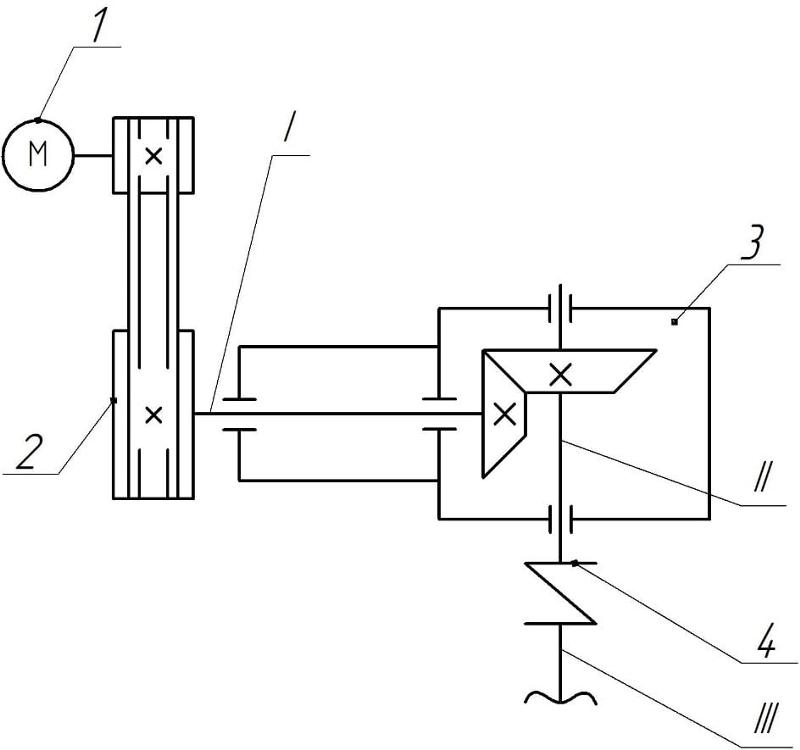 Текущий текст включает в себя все установленные юридические процедуры и свидетельские показания, отражающие условия жизни обвиняемой и окружающего ее мира. Документ, фиксирующий события в штаб-квартире инквизиции, имеет лит…

Об обороне Большого Константинопольского дворца: Предложение о местонахождении и идентификации острога или квартала Нумеры.

Были проведены многочисленные и исчерпывающие исследования оборонительной системы города Константинополя, его войск, количества имевшихся в разные династические периоды, его успешных и неприступных феодосийских стен и того, как они выстояли, отражая атаки иностранных врагов во время более десяти столетий (без учета ци…

Мораль и насилие: принципы исторической и социальной картографии ценностей

В этой статье мы стремимся выявить элементы, составляющие часть картографии власти, последовательность работ связанных с более крупным исследованием.В криминальных процессах Малле-PR в Бразилии удалось найти точки, которые предполагают довольно скрытую мораль в обществе, которая настраивает осуществление власти, пересекая предметы, институты и знания. ..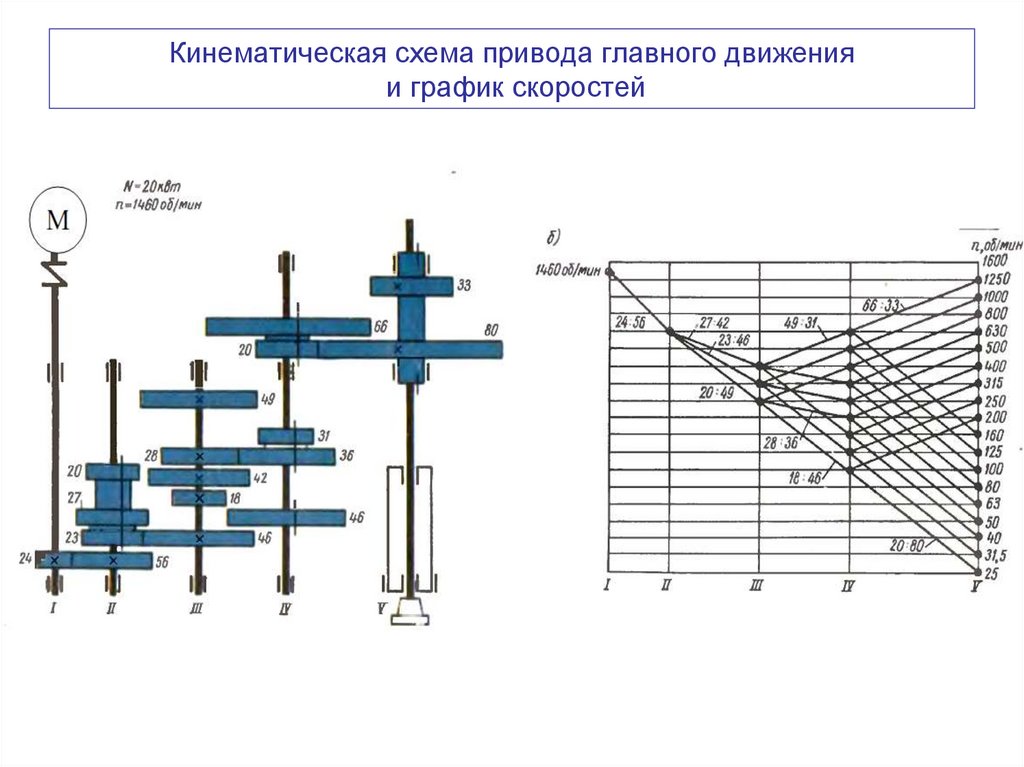

Предварительное исследование плана социальных пособий как мотивационного фактора человеческого капитала в государственных университетах Анголы, Universidade Cuito Cuanavale-Cuando Cubango-Angola

Исследование было сосредоточено на выявлении, анализе и обсуждении результатов на уровне валоризации этого капитал. Для исследования хороший обзор чтения по управлению людьми, навыкам управления знаниями и обучению и развитию людей в организациях, а также нормативно-правовой базе по повышению ценности человеческого капитала …

Рецензируемые статьи

Подтверждение Карнейро: нехватка ресурсов и досовременная война

В 1970 году Роберт Карнейро представил теорию, названную ограничением. Теория предполагает, что воздействие определенных условий окружающей среды является основным фактором, определяющим конфликт в досовременную эпоху. Хорошо принятая в одних кругах, другие тщательно изучали, была ли эта теория настолько действенной, как она утверждала (см. , например, симпозиум, опубликованный американским …

«Перо сильнее меча»: популярная этика в Японии периода Эдо).

К концу периода Эдо в Японии (1603–1868) каждая из трех основных религиозных традиций Японии, по-видимому, нашла формально определенные роли в японской культуре и политике. В середине XIX века Н. Сонтоку (1787–1858) кратко резюмировал свое понимание их более формализованной роли следующим образом: «Синтоизм — это путь, который…

Этическая дилемма зеленой экономики: изучение человеческого и экологические затраты на добычу кобальта в ДРК

…

Современные подходы к преподаванию программы бизнес-образования в Нигерии: уроки пандемии Covid-19.

Закрытие учебных заведений в стране, вызванное последствиями COVID-19, требует более эффективных подходов к обучению учащихся, чтобы предотвратить ненужные задержки в процессе преподавания и обучения. Таким образом, в данной статье были рассмотрены значение и задачи бизнес-образования, бизнес-образования. …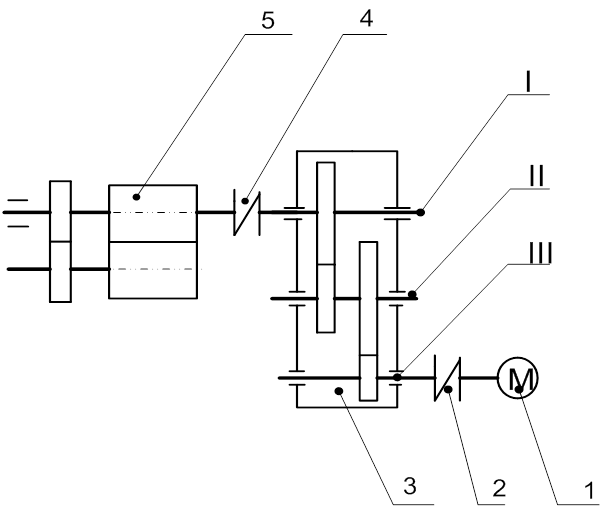

Повторное основание исполнительных воображаемых образов и коллективные обозначения организационной функциональной композиции в «Дьяволе на кресте» Нгуги Ва Тионго (1980)

Через частоту фрейма импортированного государства и вестернизацию африканского политического порядка социальная конструкция африканской бюрократии предстает как структурное устройство абстракции, эксплуатации и жестокости. Затем, через систему отсчета с импортом концептуальной юридической координации и перцептивного представления…

США Регистрационный номер: 0423089 | Идентификатор членства OARS: 4636/AO | Идентификационный номер налогоплательщика США (Emp. ID): 098-0673227 | Лицензия №: 42125/022010/1186 | Рег. №: 430374 | Импорт-экспорт: 11027
Группа, сертифицированная по стандарту ISO 9001:2005. Global Journals Logo® является зарегистрированным товарным знаком Global Journals Incorporated и Global Journals Private Limited. Патенты на корпоративные исследования находятся на рассмотрении. Авторские права © Global Journals, 2016 г. Лицензия Creative Commons Журналы с открытым доступом от Global Journals находятся под лицензией Creative Commons Attribution 4.0 International License.

Кинематические уравнения и кинематические графики

Урок 4 этого раздела в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом Уроке подчеркивалось, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики зависимости скорости от времени можно использовать для определения числовых значений и отношений между величинами перемещения (d), скорости (v), ускорения (a) и времени (t). В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и предсказания численных значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (т). Таким образом, теперь есть два метода решения задач, связанных с числовыми соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем отношения между этими двумя методами.

Пример задачи — графическое решение

Рассмотрим объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд. секунды. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.

Горизонтальная часть графика изображает движение с постоянной скоростью, что соответствует словесному описанию. Участок графика с положительным наклоном (т. е. с наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося с 5 м/с до 15 м/с. Наклон линии можно вычислить, используя коэффициент подъема относительно пробега. Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с ² . По графику скорость-время определено ускорение объекта, равное 2 м/с ² в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.

Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.

Прямоугольник	Треугольник
Площадь = основание * высота Площадь = (10 с) * (5 м/с) Площадь = 50 м	Площадь = 0,5 * основание * высота Площадь = 0,5 * (5 с) * (10 м/с) Площадь = 25 м

Общая площадь (прямоугольник плюс треугольник) равна 75 м. кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.

Приведенное выше обсуждение иллюстрирует, как графическое представление движения объекта можно использовать для извлечения числовой информации об ускорении и смещении объекта. После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения. Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут быть использованы для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.

 

Пример задачи — решение с использованием кинематического уравнения

Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематического уравнения. Вербальное описание движения было следующим:

Объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд

Кинематические уравнения могут быть применены к любому движению, для которого ускорение является постоянным. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд. В таблице ниже перечислены заданные параметры движения.

t = 0 с – 5 с	т = 5 с – 10 с
v i = 5 м/с v f = 5 м/с t = 5 с a = 0 м/с 2	v i = 5 м/с v f = 15 м/с t = 5 с

Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м/с ² , несмотря на то, что это явно не указано. Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.

v _f = v _i + a*t

Здесь показаны подстановка и алгебра.

15 м/с = 5 м/с + а*(5 с)
15 м/с – 5 м/с = a*(5 с)

10 м/с = a*(5 с)

(10 м/с)/(5 с) = a

a = 2 м /с ²

Это значение ускорения объекта за время от 5 с до 10 с согласуется со значением, определяемым по наклону линии на графике скорость-время.

Перемещение объекта за все 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают в себя два совершенно разных интервала ускорения, расчеты для каждого интервала необходимо выполнять отдельно. Это показано ниже.

t = 0 с – 5 с	т = 5 с – 10 с
d = v i *t + 0,5*a*t 2 d = (5 м/с)*(5 с) +0,5*(0 м/с 2 )*(5 с) 2 d = 25 м + 0 м д = 25 м	d = ((v i + v f )/2)*t d = ((5 м/с + 15 м/с)/2)*(5 с) d = (10 м/с)*(5 с) д = 50 м

Общее перемещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.

Анализ этого простого движения иллюстрирует значение этих двух представлений движения – графика скорость-время и кинематических уравнений. Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.

Проверьте свое понимание

1. Rennata Gas движется по городу со скоростью 25,0 м/с и начинает ускоряться с постоянной скоростью -1,0 м/с ² . В конце концов Ренната полностью останавливается.

а. Представьте ускоренное движение Реннаты, нарисовав график зависимости скорости от времени. Используйте график зависимости скорости от времени, чтобы определить это расстояние.
б. Используйте кинематические уравнения для расчета расстояния, которое проходит Ренната при замедлении.

См. график и ответ

2. Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с ² в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.

а. Представьте 15 секунд движения Отто Эмиссион, нарисовав график зависимости скорости от времени. Используйте график, чтобы определить расстояние, пройденное Отто за все 15 секунд.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.

См. график и ответ

 

3. Люк Аутбелоу, человек, мастер по стрельбе из пушечного ядра, был сброшен с края обрыва с начальной восходящей скоростью +40,0 м/с. Люк ускоряется с постоянным нисходящим ускорением -10,0 м/с ² (приблизительное значение ускорения свободного падения).

а. Нарисуйте график зависимости скорости от времени для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбело, чтобы вернуться на исходную высоту скалы. Укажите это время на графике.

См. график и ответ

 

4. Чак Вагон движется с постоянной скоростью 0,5 мили/минуту в течение 10 минут. Затем Чак замедляется со скоростью -0,25 мили/мин ² в течение 2 минут.

а. Нарисуйте график скорости во времени для движения Чака Вагона. Используйте график зависимости скорости от времени, чтобы определить общее расстояние, пройденное Чаком Вагоном за 12 минут движения.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.

См. график и ответ

 

5. Вера Сайд мчится по межштатной автомагистрали со скоростью 45,0 м/с. Вера смотрит вперед и наблюдает за аварией, в результате которой посреди дороги образовалась авария. К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с ² .

а. Постройте график зависимости скорости от времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера преодолела бы до полной остановки (если бы она не столкнулась с нагромождением).
б. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд преодолела бы до полной остановки (если бы она не столкнулась с нагромождением). Столкнется ли Вера с машинами в толпе? То есть проедет ли Вера больше 50,0 метров?

См. график и ответ

 

6. Эрл Э. Бёрд движется со скоростью 30,0 м/с за 10,0 секунд. Затем он разгоняется до 3,00 м/с ² за 5,00 секунд.

а. Постройте график зависимости скорости от времени для движения Эрла Э. Бёрда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Earl E. Bird на два временных сегмента и используйте кинематические уравнения для расчета полного смещения.

См. график и ответ

Ответы на вышеуказанные вопросы

Ответ на вопрос 1

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.

Площадь = 0,5*b*h = 0,5*(25,0 с)*(25,0 м/с)

Площадь = 313 м

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Дано: v i = 25,0 м/с в ф = 0,0 м/с а = -1,0 м/с 2

Найти: д = ??

v _f ² = v _i ² + 2*a*d

(0 м/с) ² = (25,0 м/с) ² + 2 * (-1,0 м/с ² )*д

0,0 м ² /с ² = 625,0 м ² /с ² + (-2,0 м/с ² )*d

0,0 м ² /с ² – 625,0 м ² /с ² = (-2,0 м/с ² )*d

(-625,0 м ² /с ² )/(-2,0 м/с ² ) = d

313 м = д

Вернуться к вопросу 1

 

 

Ответ на вопрос 2

а. График скорости во времени для движения:

 

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.

Площадь = 0,5*b _tri *h _tri + b _rect1 *h _rect1 + b _rect2 *h _rect2

Площадь = 0,5*(5,0 с)*(10,0 м/с) + (5,0 с)*(25,0 м/с) + (10,0 с)*(35,0 м/с)

Площадь = 25 м + 125 м + 350 м

Площадь = 500 м

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Сначала найдите d за первые 5 секунд:

Дано: v i = 25,0 м/с т = 5,0 с а = 2,0 м/с 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (25,0 м/с)*(5,0 с) + 0,5*(2,0 м/с ² )*(5,0 с) ²

d = 125 м + 25,0 м

д = 150 м

Теперь найдите d за последние 10 секунд:

Дано: v i = 35,0 м/с т = 10,0 с а = 0,0 м/с 2

Найти: д = ??

(Примечание: скорость на 5-й секунде можно найти, зная, что автомобиль ускоряется с 25,0 м/с до +2,0 м/с ² на 5 секунд. Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)

d = v _i *t + 0,5*a*t ²

d = (35,0 м/с)*(10,0 с) + 0,5*(0,0 м/с ² )*(10,0 с) ²

d = 350 м + 0 м

d =350 м

Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (150 м + 350 м):

расстояние = 500 м

Вернуться к вопросу 2

 

 

Ответ на вопрос 3

а. График скорость-время для движения:

б. Время подъема и падения на исходную высоту в два раза превышает время подъема на пик. Таким образом, решение заключается в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.

Дано: v i = 40,0 м/с v f = 0,0 м/с а = -10,0 м/с 2

Найти: т до = ?? 2*t вверх = ??

v _f = v _i + a*t _вверх

0 м/с = 40 м/с + (-10 м/с2)*t _до

(10 м/с ² )*t _до = 40 м/с

t _up = (40 м/с)/(10 м/с ² )

t _до = 4,0 с

2*t _до = 8,0 с

Вернуться к вопросу 3

 

 

 

Ответ на вопрос 4

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.

Площадь = b _{прямоугольная} *h _{прямоугольная} + 0,5*b _{тройная} *h _{тройная}

Площадь = (10,0 мин)*(0,50 мили/мин) + 0,5*(2,0 мин)*(0,50 мили/мин)

Площадь = 5 миль + 0,5 мили

Площадь = 5,5 мили

б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.

Сначала найдите d за первые 10 минут:

Дано: v i = 0,50 миль/мин т = 10,0 мин а = 0,0 миль/мин 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (0,50 миль/мин)*(10,0 мин) + 0,5*(0,0 миль/мин ² )*(10,0 мин) ²

d = 5,0 миль + 0 миль

d = 5,0 миль

Теперь найдите d за последние 2 минуты:

Дано: v i = 0,50 миль/мин т = 2,0 мин а = -0,25 миль/мин 2

Найти: д = ??

d = v _i *t + 0,5*a*t ²

d = (0,50 миль/мин)*(2,0 мин) + 0,5*(-0,25 м/с ² )*(2,0 мин) ²

d = 1,0 мили + (-0,5 мили)

d = 0,5 мили

Общее расстояние за 12 минут движения равно сумме этих двух расчетов расстояния (5,0 миль + 0,5 мили):

расстояние = 5,5 мили

Вернуться к вопросу 4

 

 

Ответ на вопрос 5

а. График скорость-время для движения:

Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.

Площадь = 0,5*b*h = 0,5*(4,5 с)*(45,0 м/с)

Площадь = 101 м

 

б.

Дано: v i = 45,0 м/с v f = 0,0 м/с а = -10,0 м/с 2

Найти: д = ??

v _f ² = v _i ² + 2*a*d

(0 м/с) ² = (45,0 м/с) ² + 2 * (-10,0 м/с ² )*d

0,0 м ² /с ² = 2025,0 м ² /с ² + (-20,0 м/с ² )*d

0,0 м ² /с ² – 2025,0 м ² /с ² = (-20,0 м/с ² )*d

(-2025,0 м ² /с ² )/(-20,0 м/с ² ) =d

101 м =d

Так как место аварии находится менее чем в 101 м от Веры, она действительно врежется в нагромождение перед полной остановкой (если не отклонится в сторону).