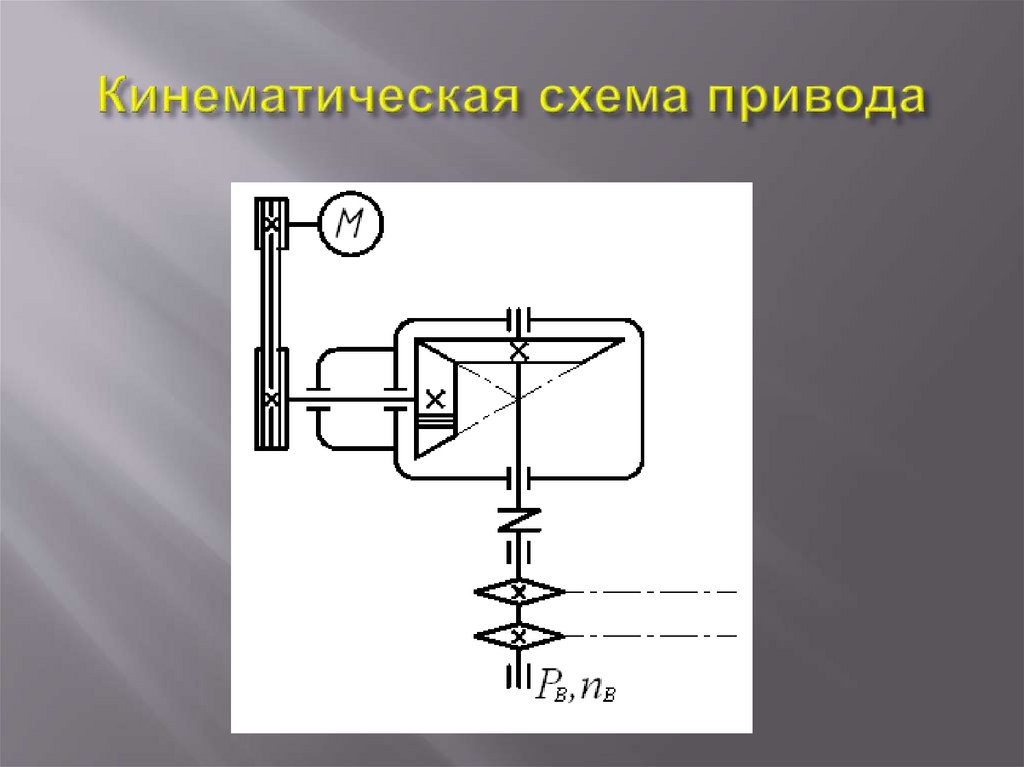
1. Кинематическая схема привода
| Исходные данные: Тяговая сила цепи Скорость тяговой цепи Шаг тяговой цепи Число зубьев звездочки Срок службы привода лет |
Валы: В1 – двигателя, В2 – быстроходный редуктора, В3. тихоходный редуктора, В4 – рабочей машины (тяговой цепи) | |
2.
 Выбор электродвигателя. Кинематический и силовой расчет привода
Выбор электродвигателя. Кинематический и силовой расчет привода2.1. Определение номинальной мощности и номинальной частоты вращения двигателя
Исходные данные:
– тяговая сила цепи конвейера,
– скорость цепи конвейера.
Определяем требуемую мощность конвейера:
Определяем КПД привода:
где – КПД закрытой передачи (цилиндрический редуктор),
– КПД открытой передачи (клиноременная передача),
– КПД муфты,
– КПД подшипников качения (по кинематической схеме в редукторе две пары подшипников),
– КПД подшипников скольжения (по схеме
на приводном валу конвейера одна пара
подшипников).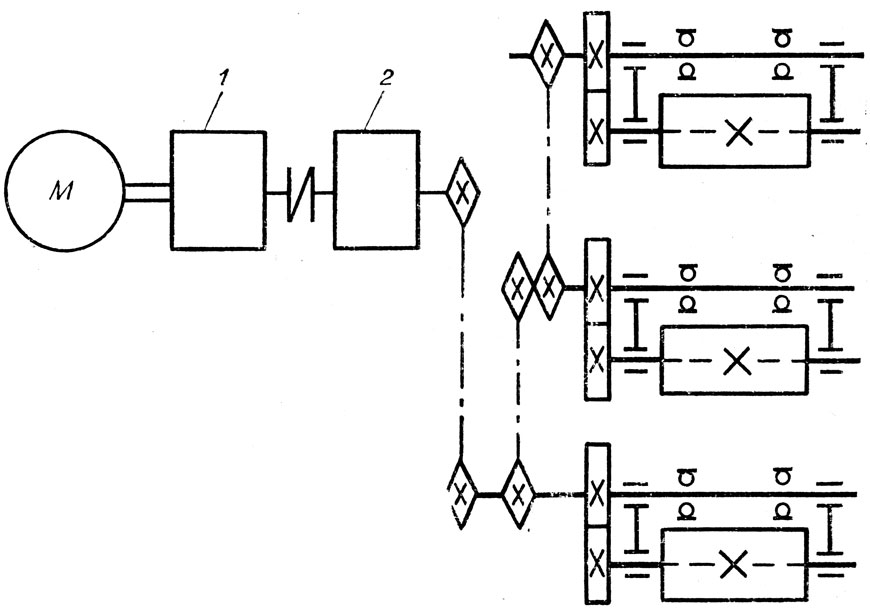
Находим требуемую мощность двигателя:
.
Из условия потаблице диапазонов мощностей трехфазных асинхронных двигателей серии 4А (А.Е. Шейнблит «Курсовое проектирование деталей машин», таблица 2.1, стр.41) выбираем ближайшее к требуемой мощности двигателя значение номинальной мощности.
По значению номинальной мощности выбираем четыре варианта типа двигателя серии А4:
Вариант
Тип двигателя
Номинальная мощность
Частота вращения, об/мин
синхронная
При номинальном режиме
1
4АМ112МАУ3
2,2
750
700
2
4АМ100L6У3
2,2
1000
950
3
4АМ90L4У3
2,2
1500
1425
4
4АМ80В2У3
2,2
3000
2850
2.
 2. Определение передаточного числа привода
2. Определение передаточного числа приводаИсходные данные:
– скорость тяговой цепи конвейера,
– число зубьев звездочки,
– шаг тяговой цепи.
Определяем частоту вращения приводного вала конвейера:
– диаметр барабана,
.
Находим передаточное число привода для каждого варианта: ,
,,,.
Передаточное число привода .
Рекомендуемые значения передаточных чисел для открытой ременной и закрытой цилиндрической зубчатой передач соответственно:
,.
Следовательно, передаточное число привода .
В этот
промежуток попадают передаточные числа
для первого и второго вариантов двигателя.
Из двух вариантов выбираем второй (,),
так как первый вариант (;)
не рекомендуется для приводов общего
назначения.
Выбрали двигатель 4АМ100L6У3
Производим разбивку передаточного числа привода: ,
2.3. Кинематический и силовой расчет привода
Индексом Б обозначены параметры быстроходного вала, Т – тихоходного, дв – двигателя, вых – конвейера.
Кинематические характеристики:
Частоты вращения:
,
,
,
.
Угловые скорости:
,
,
,
.
Силовые характеристики:
Мощности:
,
,
,
.
Вращающие моменты:
,,
,
.
Тип двигателя 4АМ100L6 У3 ; | |||||||
Параметр | Передача | Параметр | Вал | ||||
закрытая цилиндр. зубчатая | открытая ременная | двигателя | редуктора | тяговой цепи | |||
быстроходный | тихоходный | ||||||
Передаточное число | 5,0 | 3,68 | Расчетная мощность Р, кВт | 1,69 | 1,64 | 1,59 | 1,54 |
Угловая скорость | 99,48 | 27,03 | 5,41 | 5,41 | |||
КПД | 0,97 | 0,97 | Частота вращения п, об/мин | 950 | 258,15 | 51,63 | 51,63 |
Вращающий момент Т, | 16,98 | 60,91 | 293,96 | 285,2 | |||
Кинематическая схема привода технологической машины.
 Обозначения элементов привода на кинематических схемах
Обозначения элементов привода на кинематических схемахПохожие презентации:
Грузоподъемные машины. (Лекция 4.1.2)
Зубчатые передачи
Гидравлический домкрат в быту
Детали машин и основы конструирования
Газораспределительный механизм
Свайные фундаменты. Классификация. (Лекция 6)
Ременные передачи
Редукторы
Техническая механика. Червячные передачи
Фрезерные станки. (Тема 6)
1. Прикладная механика
ДавидовичИгорь Юрьевич
(курс лекций)
Кинематическая схема привода
технологической машины.
Обозначения элементов привода
на кинематических схемах.
к. 205, корпус 1, т. 80222410512
E-mail: [email protected]
1
2. Источник движения
м2
3. Передача гибкой связью (клиноременная)
34. Передача зацеплением (цепная)
xx
4
5. Передача зацеплением (зубчатая цилиндрическая)
xx
5
6. Передача зацеплением (зубчатая коническая)
67.
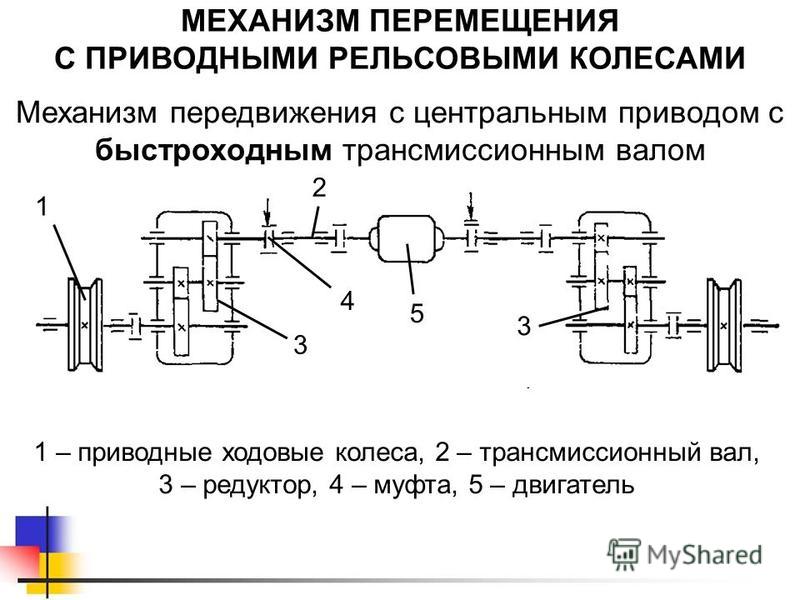 Передача зацеплением (червячная) 7
Передача зацеплением (червячная) 7МУФТЫ
жесткая
упругая
8
Цилиндрический редуктор
ЦР
9
Конический редуктор
КР
10
Коническо-цилиндрический
КЦР
11
Червячный редуктор
ЧР
12
Рабочие органы машин
Цепной транспортер
x
x
x
x
Обозначение на кинематической схеме
13
Рабочие органы машин
Ленточный транспортер
Обозначение на кинематической схеме
14
Рабочие органы машин
Винтовой (шнековый) транспортер
а – горизонтальный транспортер
б – вертикальный транспортер
Обозначение на кинематической схеме
15
Рабочие органы машин
Грузоподъемное устройство (таль)
m
Обозначение на кинематической схеме
16
Кинематическая схема привода
м
ЧР
Составить кинематическую схему для
привода, состоящего из электродвигателя,
упругой муфты и червячного редуктора
17
Кинематическая схема привода
Х
м
Составить кинематическую схему
для привода, состоящего из двигателя,
упругой муфты, цилиндрического
редуктора, цепной передачи и
приводного вала цепного транспортера
x
x
x
x
ЦР
Х
18
Кинематическая схема привода
М
ЦР
x
Привод, состоящий из двигателя,
упругой муфты, цилиндрического
редуктора и цепной передачи
x
19
Кинематическая схема привода
М
ЦР
X
X
Привод, состоящий из электродвигателя,
упругой муфты, цилиндрического
редуктора и клиноременной передачи
20
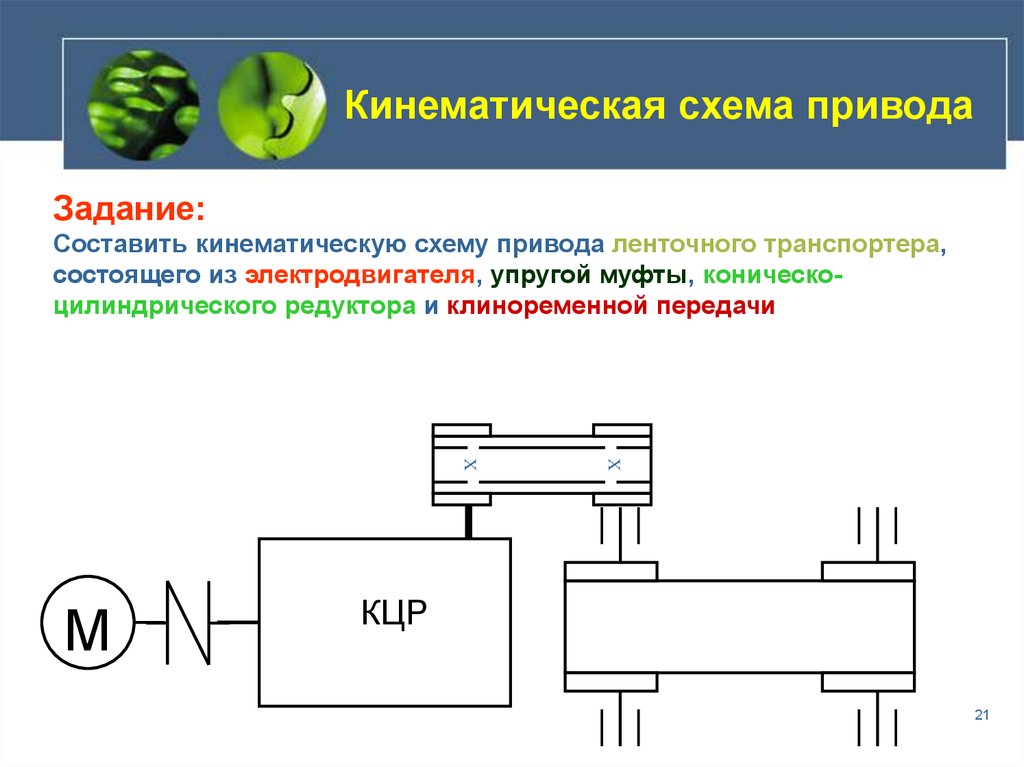
Кинематическая схема привода
Задание:
Составить кинематическую схему привода ленточного транспортера,
состоящего из электродвигателя, упругой муфты, коническоцилиндрического редуктора и клиноременной передачи
X
X
М
КЦР
21
Кинематическая схема привода
Задание:
ЧР
x
Составить кинематическую
схему привода барабана
лебедки, состоящего из:
электродвигателя
упругой муфты
червячного редуктора
цепной передачи
М
x
m
22
English Русский Правила
Кинематические уравнения и кинематические графики
Урок 4 этого раздела в классе физики был посвящен использованию графиков скорость-время для описания движения объектов.
Пример задачи — графическое решение
Рассмотрим объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд. секунды. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
секунды. Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
Горизонтальная часть графика изображает движение с постоянной скоростью, что соответствует словесному описанию. Участок графика с положительным наклоном (т. е. с наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося с 5 м/с до 15 м/с. Наклон линии можно вычислить, используя коэффициент подъема относительно пробега. Между 5 и 10 секундами скорость линии увеличивается с 5 м/с до 15 м/с и продолжается от 5 до 10 с. Это общий подъем +10 м/с и общий пробег 5 с. Таким образом, уклон (соотношение подъем/спуск) равен (10 м/с)/(5 с) = 2 м/с 2 . По графику скорость-время определено ускорение объекта, равное 2 м/с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика зависимости скорости от времени. Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Площадь между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции. Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего на вершине площади прямоугольника. Это показано на диаграмме ниже.
Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
| Прямоугольник | Треугольник |
|---|---|
| Площадь = основание * высота Площадь = (10 с) * (5 м/с) Площадь = 50 м | Площадь = 0,5 * основание * высота Площадь = 0,5 * (5 с) * (10 м/с) Площадь = 25 м |
Общая площадь (прямоугольник плюс треугольник) равна 75 м.кв. Таким образом, перемещение объекта за 10 секунд движения составляет 75 метров.
Приведенное выше обсуждение иллюстрирует, как графическое представление движения объекта может использоваться для извлечения числовой информации об ускорении и смещении объекта.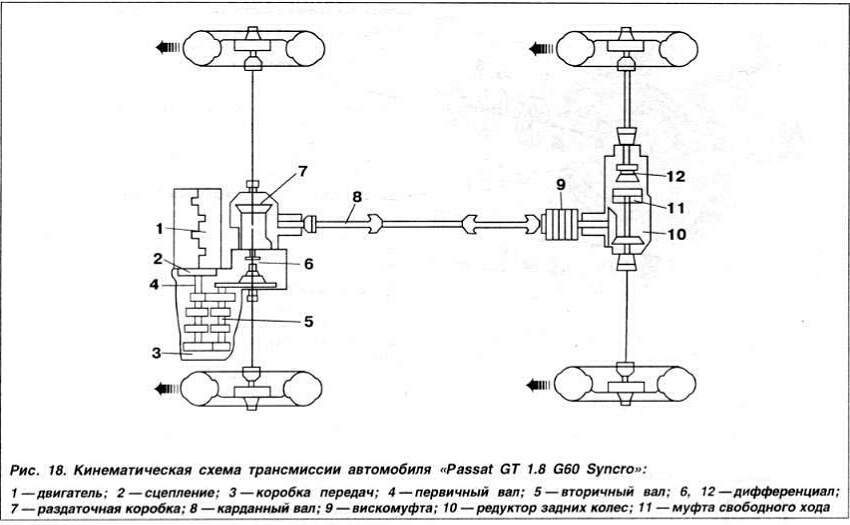 После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения. Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут быть использованы для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.
После построения график зависимости скорости от времени можно использовать для определения скорости объекта в любой момент времени в течение 10 секунд движения. Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время могут быть использованы для выявления (или определения) числовых значений и взаимосвязей между величинами смещения (d), скорости (v), ускорения (a) и времени (t) для любого заданного движения.
Пример задачи — решение с использованием кинематического уравнения
Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематического уравнения. Вербальное описание движения было следующим:
Объект, который движется с постоянной скоростью +5 м/с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м/с в течение следующих 5 секунд
Кинематические уравнения могут быть применены к любому движению, для которого ускорение является постоянным. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд. В таблице ниже перечислены заданные параметры движения.
Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения для первых 5 секунд не смешивались с параметрами движения для последних 5 секунд. В таблице ниже перечислены заданные параметры движения.
| t = 0 с – 5 с | т = 5 с – 10 с |
|---|---|
| v i = 5 м/с v f = 5 м/с t = 5 с a = 0 м/с 2 | v i = 5 м/с v f = 15 м/с t = 5 с |
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м/с 2 , несмотря на то, что это явно не указано. Фраза постоянная скорость указывает на движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v f = v i + a*t
Здесь показаны подстановка и алгебра.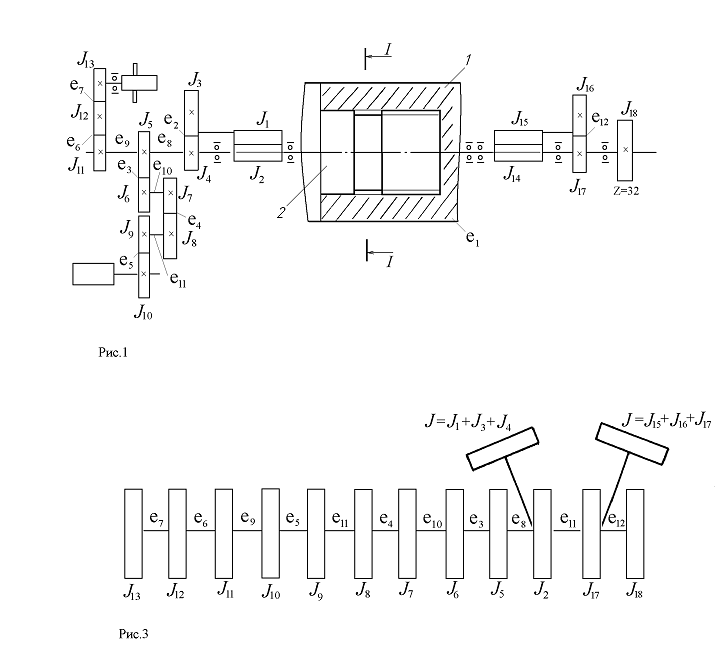
15 м/с = 5 м/с + а*(5 с)
15 м/с – 5 м/с = a*(5 с)
10 м/с = a*(5 с)
(10 м/с)/(5 с) = a
a = 2 м /с 2
Это значение ускорения объекта за время от 5 с до 10 с согласуется со значением, определяемым по наклону линии на графике скорость-время.
Смещение объекта за все 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают в себя два совершенно разных интервала ускорения, расчеты для каждого интервала необходимо выполнять отдельно. Это показано ниже.
| t = 0 с – 5 с | т = 5 с – 10 с |
|---|---|
| d = v i *t + 0,5*a*t 2 d = (5 м/с)*(5 с) +0,5*(0 м/с 2 )*(5 с) 2 d = 25 м + 0 м д = 25 м | d = ((v i + v f )/2)*t d = ((5 м/с + 15 м/с)/2)*(5 с) d = (10 м/с)*(5 с) д = 50 м |
Общее перемещение за первые 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует значение этих двух представлений движения – графика скорость-время и кинематических уравнений. Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м/с и начинает ускоряться с постоянной скоростью -1,0 м/с 2 . В конце концов Ренната полностью останавливается.
а. Представьте ускоренное движение Реннаты, нарисовав график зависимости скорости от времени. Используйте график зависимости скорости от времени, чтобы определить это расстояние.
б. Используйте кинематические уравнения для расчета расстояния, которое проходит Ренната при замедлении.
См. график и ответ
2. Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
Отто Эмиссионс едет на своей машине со скоростью 25,0 м/с. Отто ускоряется со скоростью 2,0 м/с 2 в течение 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
а. Представьте 15 секунд движения Отто Эмиссион, нарисовав график зависимости скорости от времени. Используйте график, чтобы определить расстояние, пройденное Отто за все 15 секунд.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения для расчета общего расстояния, пройденного за все 15 секунд.
См. график и ответ
3. Люк Отбелоу, человек, мастер по стрельбе из пушечного ядра, был сброшен с края обрыва с начальной восходящей скоростью +40,0 м/с. Люк ускоряется с постоянным нисходящим ускорением -10,0 м/с 2 (приблизительное значение ускорения свободного падения).
а. Нарисуйте график зависимости скорости от времени для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбело, чтобы вернуться на исходную высоту скалы. Укажите это время на графике.
См. график и ответ
4. Чак Вагон движется с постоянной скоростью 0,5 мили/мин в течение 10 минут. Затем Чак замедляется со скоростью -0,25 мили/мин 2 в течение 2 минут.
а. Нарисуйте график скорости во времени для движения Чака Вагона. Используйте график зависимости скорости от времени, чтобы определить общее расстояние, пройденное Чаком Вагоном за 12 минут движения.
б. Наконец, разбейте движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
См. график и ответ
5. Вера Сайд мчится по межштатной автомагистрали со скоростью 45,0 м/с. Вера смотрит вперед и наблюдает за аварией, в результате которой посреди дороги образовалась авария. К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
К моменту, когда Вера бьет по тормозам, она находится в 50,0 м от пайлапа. Она замедляется со скоростью -10,0 м/с 2 .
а. Постройте график зависимости скорости от времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера преодолела бы до полной остановки (если бы она не столкнулась с нагромождением).
б. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд преодолела бы до полной остановки (если бы она не столкнулась с нагромождением). Столкнется ли Вера с машинами в толпе? То есть проедет ли Вера больше 50,0 метров?
См. график и ответ
6. Эрл Э. Берд движется со скоростью 30,0 м/с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м/с 2 в течение 5,00 секунд.
a.Построить график зависимости скорости от времени для движения Эрла Э. Бёрда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Earl E. Bird на два временных сегмента и используйте кинематические уравнения для расчета полного смещения.
См. график и ответ
Ответы на вышеуказанные вопросы
Ответ на вопрос 1
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(25,0 с)*(25,0 м/с)
Площадь = 313 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (25,0 м/с) 2 + 2 * (-1,0 м/с 2 )*д
0,0 м 2 /с 2 = 625,0 м 2 /с 2 + (-2,0 м/с 2 )*d
0,0 м 2 /с 2 – 625,0 м 2 /с 2 = (-2,0 м/с 2 )*d
(-625,0 м 2 /с 2 )/(-2,0 м/с 2 ) = d
313 м = д
Вернуться к вопросу 1
Ответ на вопрос 2
а. График скорости во времени для движения:
График скорости во времени для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b rect1 *h rect1 + b rect2 *h rect2
Площадь = 0,5*(5,0 с)*(10,0 м/с) + (5,0 с)*(25,0 м/с) + (10,0 с)*(35,0 м/с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (25,0 м/с)*(5,0 с) + 0,5*(2,0 м/с 2 )*(5,0 с) 2
d = 125 м + 25,0 м
д = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
| Найти: д = ?? |
(Примечание: скорость на 5-й секунде можно найти, зная, что автомобиль ускоряется с 25,0 м/с до +2,0 м/с 2 на 5 секунд. Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
Это приводит к изменению скорости a*t = 10 м/с и, следовательно, к скорости 35,0 м/с.)
d = v i *t + 0,5*a*t 2
d = (35,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 350 м + 0 м
d =350 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (150 м + 350 м):
расстояние = 500 м
Вернуться к вопросу 2
Ответ на вопрос 3
а. График скорость-время для движения:
б. Время подъема и падения на исходную высоту в два раза превышает время подъема на пик. Таким образом, решение заключается в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
| Найти: т до = ?? 2*t вверх = ?? |
v f = v i + a*t вверх
0 м/с = 40 м/с + (-10 м/с2)*t вверх
(10 м/с 2 )*t до = 40 м/с
t up = (40 м/с)/(10 м/с 2 )
т до = 4,0 с
2*t до = 8,0 с
Вернуться к вопросу 3
Ответ на вопрос 4
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b прямоугольная *h прямоугольная + 0,5*b тройная *h тройная
Площадь = (10,0 мин)*(0,50 мили/мин) + 0,5*(2,0 мин)*(0,50 мили/мин)
Площадь = 5 миль + 0,5 мили
Площадь = 5,5 мили
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 минут:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(10,0 мин) + 0,5*(0,0 миль/мин 2 )*(10,0 мин) 2
d = 5,0 миль + 0 миль
d = 5,0 миль
Теперь найдите d за последние 2 минуты:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (0,50 миль/мин)*(2,0 мин) + 0,5*(-0,25 м/с 2 )*(2,0 мин) 2
d = 1,0 мили + (-0,5 мили)
d = 0,5 мили
Общее расстояние за 12 минут движения равно сумме этих двух расчетов расстояния (5,0 миль + 0,5 мили):
расстояние = 5,5 мили
Вернуться к вопросу 4
Ответ на вопрос 5
а. График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5*b*h = 0,5*(4,5 с)*(45,0 м/с)
Площадь = 101 м
б.
Дано:
| Найти: д = ?? |
v f 2 = v i 2 + 2*a*d
(0 м/с) 2 = (45,0 м/с) 2 + 2 * (-10,0 м/с 2 )*d
0,0 м 2 /с 2 = 2025,0 м 2 /с 2 + (-20,0 м/с 2 )*d
0,0 м 2 /с 2 – 2025,0 м 2 /с 2 = (-20,0 м/с 2 )*d
(-2025,0 м 2 /с 2 )/(-20,0 м/с 2 ) =d
101 м =d
Так как место аварии находится менее чем в 101 м от Веры, она действительно врежется в нагромождение перед полной остановкой (если не отклонится в сторону).
Вернуться к вопросу 5
Ответ на вопрос 6
а. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5*b tri *h tri + b 1 *ч 1 + б 2 *ч 2
Площадь = 0,5*(5,0 с)*(15,0 м/с) + (10,0 с)*(30,0 м/с) + (5,0 с)*(30,0 м/с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
б. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d за первые 10 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(10,0 с) + 0,5*(0,0 м/с 2 )*(10,0 с) 2
d = 300 м + 0 м
d =300 м
Теперь найдите d за последние 5 секунд:
Дано:
| Найти: д = ?? |
d = v i *t + 0,5*a*t 2
d = (30,0 м/с)*(5,0 с) + 0,5*(3,0 м/с 2 )*(5,0 с) 2
d = 150 м + 37,5 м
д = 187,5 м
Общее расстояние за 15 секунд движения равно сумме этих двух расчетов расстояния (300 м + 187,5 м):
расстояние = 488 м
Вернуться к вопросу 6
Карта механики — Системы с ременным и зубчатым приводом
Системы с ременным и шкивным приводом, а также системы с зубчатым приводом представляют собой распространенные способы, с помощью которых инженеры передают вращательное движение и крутящий момент с одного вала на другой. Ремни обеспечивают гибкость, поскольку валы не обязательно должны располагаться рядом друг с другом, а шестерни чаще используются в приложениях с высокими нагрузками.
Ремни обеспечивают гибкость, поскольку валы не обязательно должны располагаться рядом друг с другом, а шестерни чаще используются в приложениях с высокими нагрузками.
| Ремни и шкивы часто используются для передачи движения и крутящего момента от одного вала к другому. | Шестерни— еще один распространенный способ передачи движения и крутящего момента с одного вала на другой. |
Положение, скорость и ускорение в системах с ременным приводом
На приведенной ниже схеме показана простая система с ременным приводом. Шкив A и шкив B имеют каждый свой радиус и соединены ремнем, который, как мы предполагаем, не проскальзывает относительно шкивов. Каждый шкив вращается с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно; однако движение ремня можно использовать для связи движения двух шкивов.
На приведенной выше диаграмме показана простая система с ременным приводом, соединяющая шкив A и шкив B.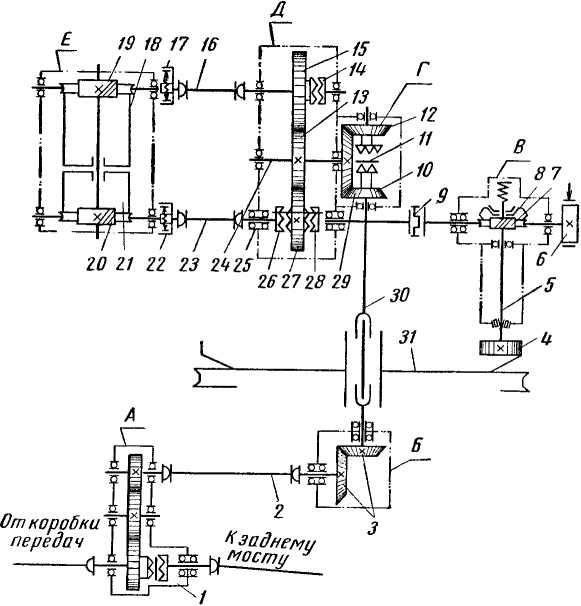
В качестве ограничения мы можем предположить, что скорость шкива будет одинаковой по всему контуру в любой момент времени. Если бы это было не так, ремень бы сбивался в одних местах и растягивался в других. Если ремень не проскальзывает, скорость ремня будет равна скорости края каждого из двух шкивов. Установив эти две скорости равными друг другу и работая в обратном направлении, чтобы связать их с угловыми скоростями, мы получим среднее уравнение ниже. Взятие интеграла или производной позволяет нам также связать угловые смещения или угловые ускорения с помощью подобных уравнений.
| Угловые смещения: | \[r_{A}(\Delta\Theta_{A})=r_{B}(\Delta\Theta_{B})\] |
|---|---|
| Угловые скорости: | \[r_{A}\omega_{A}=r_{B}\omega_{B}\] |
| Угловые ускорения: | \[r_{A}\alpha_{A}=r_{B}\alpha_{B}\] |
Если у нас есть более сложная серия ремней и шкивов, мы будем анализировать систему шаг за шагом. Это будет включать в себя шкивы, соединенные ремнями, как указано выше, а также шкивы, соединенные валом, как показано со шкивами B и C на диаграмме ниже.
Это будет включать в себя шкивы, соединенные ремнями, как указано выше, а также шкивы, соединенные валом, как показано со шкивами B и C на диаграмме ниже.
При наличии шкивов на одном валу угловые смещения, угловые скорости и угловые ускорения будут одинаковыми.
| \[\Delta \Theta_{B}=\Delta \Theta_{C}\] | \[\omega_{B}=\omega_{C}\] | \[\alpha_{B}=\alpha_{C}\] |
Если мы знаем угловое смещение, угловую скорость или угловое ускорение шкива A, мы могли бы найти угловое смещение, угловую скорость или угловое ускорение шкива D, совершая одно взаимодействие за раз (определяя движение шкива В, затем С, затем Г).
Положение, скорость и ускорение в зубчатых передачах
На приведенной ниже схеме показана простая зубчатая передача.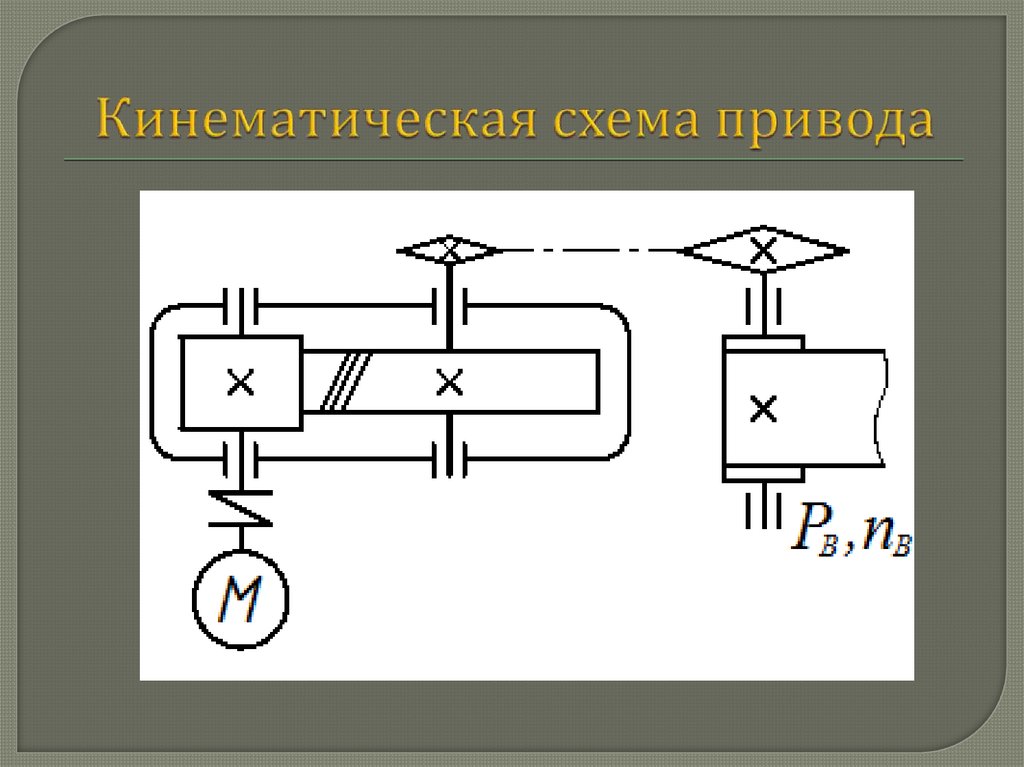 Механизм A и механизм B имеют каждый свой собственный радиус и взаимодействуют в точке контакта. Каждая шестерня вращается с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно; однако движение зубьев в точке контакта можно использовать для связи движения одной шестерни с другой.
Механизм A и механизм B имеют каждый свой собственный радиус и взаимодействуют в точке контакта. Каждая шестерня вращается с фиксированной осью и поэтому будет следовать этим кинематическим правилам отдельно; однако движение зубьев в точке контакта можно использовать для связи движения одной шестерни с другой.
В качестве ограничения можно предположить, что скорость зубьев в точке контакта будет одинаковой. Если бы это было не так, зубья одной шестерни проходили бы через зубья другой шестерни. Установив эти две скорости равными друг другу и работая в обратном порядке, чтобы связать угловые скорости, мы находим второе уравнение ниже. Взятие интеграла или производной позволяет нам также связать угловые смещения или угловые ускорения с помощью подобных уравнений.
| Угловые смещения: | \[r_{A}(\Delta\Theta_{A})=-r_{B}(\Delta\Theta_{B})\] |
|---|---|
| Угловые скорости: | \[r_{A}\omega_{A}=-r_{B}\omega_{B}\] |
| Угловые ускорения: | \[r_{A}\alpha_{A}=-r_{B}\alpha_{B}\] |
Вы заметите, что приведенные выше уравнения совпадают с уравнениями для систем с ременным приводом, за исключением знака минус в правой части каждого уравнения.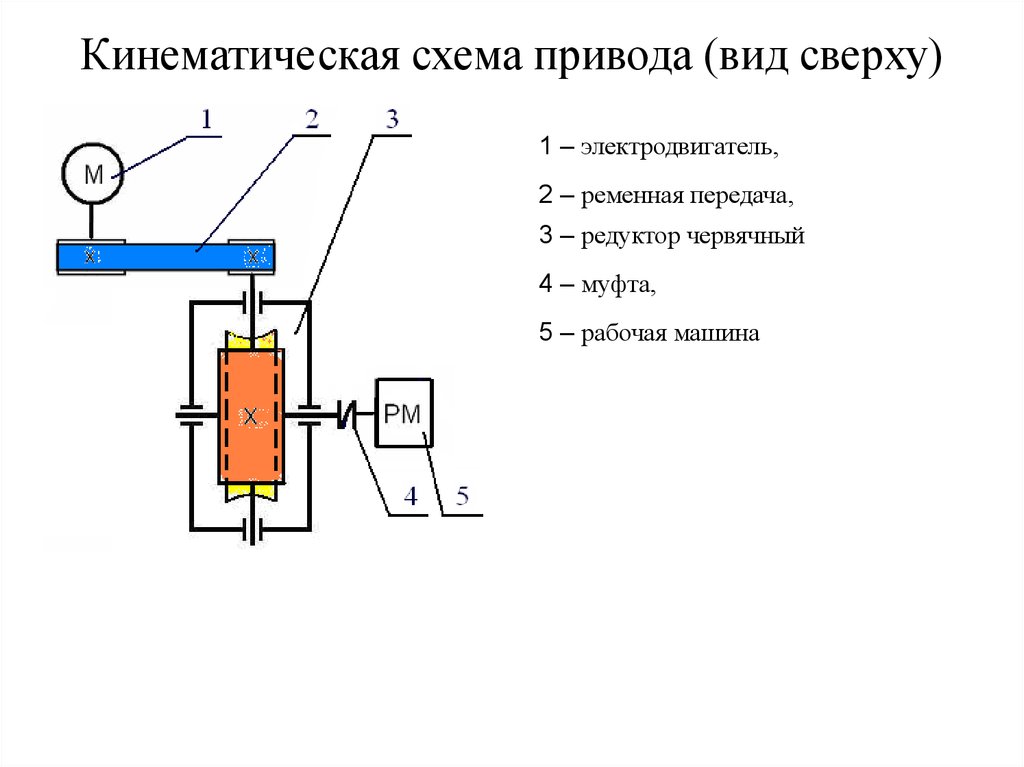 Это связано с тем, что зацепленные шестерни вращаются в противоположных направлениях (если одна шестерня вращается по часовой стрелке, другая будет вращаться против часовой стрелки), в то время как шкивы в системах с ременным приводом всегда вращаются в одном направлении.
Это связано с тем, что зацепленные шестерни вращаются в противоположных направлениях (если одна шестерня вращается по часовой стрелке, другая будет вращаться против часовой стрелки), в то время как шкивы в системах с ременным приводом всегда вращаются в одном направлении.
Подобно системам с ременным приводом, мы можем иметь составные зубчатые передачи с тремя или более передачами, как показано на рисунке ниже. В этих сценариях у нас также, вероятно, будут шестерни, которые соединены через вал, такие как синяя и желтая шестерни, показанные ниже. В таких ситуациях шестерни на одном валу будут иметь соответствующие угловые смещения, угловые скорости и угловые ускорения. Как и в системах с ременным приводом, вам просто нужно перемещать зубчатую передачу по одному шагу за раз, применяя правильный набор уравнений для соответствия каждому шагу взаимодействия.
На приведенной выше анимированной диаграмме показана составная зубчатая передача. Красная и синяя шестерни взаимодействуют через зацепление зубьев, затем синяя и желтая шестерни находятся на одном валу, затем, наконец, желтая и зеленая шестерни взаимодействуют через зацепление зубьев.
Концепция, которая обычно используется в зубчатых передачах, но обычно не используется в системах с ременным приводом, — это концепция передаточного числа . Для любой зубчатой передачи передаточное число определяется как угловая скорость на входе, деленная на угловую скорость на выходе. Основываясь на приведенных выше уравнениях, мы также можем доказать, что отношение угловых перемещений или угловых ускорений будет аналогично равно передаточному числу. Передаточное число всегда определяется как положительное число; однако вам все равно придется использовать интуицию, чтобы определить направление выхода.
| \[Передаточное число=\frac{\omega_{вход}}{\omega_{выход}}=\frac{\Delta\Theta_{вход}}{\Delta\Theta_{выход}}=\frac {\alpha_{вход}}{\alpha_{выход}}\] |
В простой двухступенчатой системе передаточное отношение будет равно радиусу выходной шестерни, деленному на радиус входной шестерни, или числу зубьев выходной шестерни, деленному на количество зубьев на входная шестерня (поскольку количество зубьев будет прямо пропорционально радиусу).