Класс точности h: Класс точности станка | MoscowShpindel

Содержание

Класс точности станка | MoscowShpindel

На каждом виде станков проводится испытание на соответствие норме точности. Результаты испытания записываются в акт, который вкладывается в паспорт станка. Каждый тип станков имеет ГОСТ, который регламентирует допустимые отклонения во всех проверках. Количество проверок для разных типов станков бывает различным. Некоторые модели настольных широкоуниверсальных фрезерных станков с ЧПУ имеют несколько десятков проверок. Все станки классифицируются по точности работы делением на классы:

На станках нормальной точности обрабатываются заготовки из проката, литья и поковок. Обозначаются буквой Н.
На станках повышенной точности (они выпускаются на базе станков с нормальной точностью, но их монтаж отличается особой тщательностью) можно обрабатывать заготовки такого же производства, но с более точным выполнением всех работ. Обозначаются буквой П.
На станках высокой точности (обозначаются буквой В) и особо высокой точности (буквой А) более высокая точность достигается за счет специальных конструктивных особенностей и высокой точности изготовления их узлов, а также благодаря специальным условиям эксплуатации.
На особо точных станках можно достичь наивысшей точности обработки очень ответственных деталей: делительных дисков, зубчатых колес, измерительного инструмента и других видов. Обозначаются буквой С.

Допустимые отклонения по проверкам соседних классов точности станков отличаются друг от друга в 1,6 раза. Вот таблица величин допускаемых отклонений при прямолинейном движении для станков, имеющих различный класс точности.

Класс точности станка
Н		П		В	А		С
Допустимые отклонения, микроны
10	6		4			2,5		1,6

ГОСТ 8-82 для всех видов металлорежущих станков, в том числе и настольных с ЧПУ, устанавливает стандарт общих требований к испытаниям на точность. По нему точность всех станков этого типа определяется по трем группам показателей:

точность обработки испытываемых образцов;
геометрическая точность самих станков;
дополнительные показатели.

Этот стандарт устанавливает порядок присвоения группе станков одинакового класса точности, который должен обеспечивать одинаковую точность обработки идентичных по форме и размеру образцов изделий.

Точность обработки деталей. Классы точности

Взаимозаменяемость деталей.

Выпуск велосипедов, мотоциклов, тракторов, автомобилей, электродвигателей, швейных и других машин осуществляется на заводах такими темпами, когда счет времени обработки и сборки ведется не только минутами, но и секундами. Детали этих машин должны быть изготовлены точно по чертежам и техническим условиям так, чтобы при сборке они подходили одна к другой без слесарной подгонки, что сокращает время на сборку и удешевляет стоимость изделия. Важно также, чтобы при ремонте машины новая деталь, заменяющая изношенную, могла быть установлена на ее место без подгонки. Детали, удовлетворяющие таким требованиям, называются взаимозаменяемыми. Взаимозаменяемость – это свойство деталей занимать свои места в узлах и изделиях без предварительного подбора или подгонки по месту.

Сопряжение деталей.

Две детали, подвижно или неподвижно соединяемые друг с другом, называют сопрягаемыми. Размеры, по которым происходит соединение этих деталей, называют

сопрягаемыми размерами. Размеры, по которым не происходит соединение деталей, называют свободными размерами. Примером сопрягаемых размеров может служить наружный диаметр фрезерной оправки и соответствующий ему диаметр отверстия в насадной фрезе, диаметр шейки оправки и соответствующий ему диаметр отверстия в подшипнике подвески. Примером свободных размеров может служить наружный диаметр установочных колец фрезерной оправки, длина фрезерной оправки, ширина цилиндрической фрезы.

Сопрягаемые детали должны быть выполнены взаимозаменяемыми.

Понятие о точности обработки.

Изготовить партию взаимозаменяемых деталей абсолютно одинакового размера невозможно, так как на точность обработки влияют неточность и износ станка, износ фрезы, неточности при установке и закреплении заготовки и другие причины. Как правило, все детали данной партии при обработке имеют отклонения от заданных размеров и формы. Но величины этих отклонений должны быть назначены таким образом, чтобы сопрягаемые размеры могли обеспечить сборку деталей без подгонки, т.е. чтобы детали были взаимозаменяемыми.

Конструкторы изделий при назначении величины допускаемых отклонений на сопрягаемые детали руководствуются установленными государством стандартами – ГОСТ. Ниже вкратце излагаются основные понятия о допусках и предельных отклонениях, вытекающие их ГОСТ 7713-55.

Понятие о допуске и предельных отклонениях. Величина допустимых отклонений указывается в чертежах детали со знаками плюс и минус.

Знак минус показывает, что деталь может быть изготовлена с отклонением в меньшую сторону; знак плюс показывает, что деталь может быть изготовлена с отклонением в большую сторону. Например, поставленный в чертеже бруска размер 10_-0,1 мм показывает, что брусок может быть отфрезерован так, чтобы после его обработки его размер лежал в пределах между 10 мм и 9,9 мм. Точно также поставленный в чертеже диаметр паза

10^+0,2 мм показывает, что паз может быть отфрезерован так, чтобы после обработки его размер лежал в пределах между 10 мм и 10,2 мм.

Поставленный в чертеже размер 10^+0,2_-0,1 мм показывает, что обработанная деталь будет годной, если ее размер составляет не менее 9,9 мм и не более 10,2 мм, т.е. лежит в этих пределах.

Номинальным размером называется основной расчетный размер, от которого исходят при назначении отклонений. Если в чертеже указан размер 10^+0,2 _-0,1 мм, то размер 10 мм называется номинальным.

Действительным размером называется размер, полученный при измерении обработанной детали. Размеры, между которыми может находиться действительный размер годной детали, называются

предельными размерами. Действительный размер детали с размерами 10^+0,2_-0,1 мм может лежать в пределах 10+0,2 = 10,02 мм и 10-0,1 =9,9 мм. Больший размер называется наибольшим предельным размером, а меньший – наименьшим предельным размером.

Разность между наибольшим и наименьшим предельными размерами называется допуском размера.

Верхним предельным отклонением называется разность между наибольшим предельным размером и номинальным размером.
Нижним предельным отклонением называется разность между наименьшим предельным размером и номинальным размером.

Допуск можно также определить, как разность между верхним и нижним предельными отклонениями.

Действительным отклонением называется разность между действительным и номинальным размерами.

При графическом изображении допусков отклонения размеров откладываются от линии, соответствующей номинальному размеру и называемой нулевой линией; положительные отклонения откладываются вверх от нулевой линии, а отрицательные – вниз.

Зазоры и натяги.

Если брусок с размерами грани 10_-0,1 мм посадить в паз с размерами грани 10^+0,2_+0,1 мм, то в соединении бруска с пазом получится зазор, и брусок можно будет передвигать вдоль паза. Такая посадка (сопряжение двух деталей) называется свободной. Наибольший зазор в этом случае составит 0,3 мм, а наименьший будет равен 0,1 мм.

Если же размер бруска будет 10^+0,2_+0,1 мм, а паза 10_-0,1 мм, то брусок не войдет свободно в паз и его придется вставлять с силой или запрессовывать. В соединении получится натяг

или отрицательный зазор, наименьшая величина которого равна 0,1 мм. А наибольшая 0,3 мм. Такая посадка называется неподвижной, так как брусок нельзя будет передвигать вдоль паза.

Таким образом, можно сделать следующие заключения.

Зазором называется положительная разность между размером паза и размером бруска, обеспечивающая свободу их движения относительно друг друга.
Натягом называется отрицательная разность между размером паза и размером бруска (размер бруска больше размера паза), которая после посадки бруска в паз создает неподвижное их соединение.

Посадки.

Посадкой называется характер соединения сопрягаемых деталей, определяемый разностью между размерами паза и бруска, создающий большую или меньшую свободу (зазор или натяг) их относительного перемещения или степень сопротивления взаимному перемещению. В зависимости от наличия в сопряжении бруска и паза зазора или натяга различают посадки с зазором, с натягом и переходные.

Посадками с зазором, или свободными, называют такие посадки, при которых обеспечивается возможность относительного перемещения сопряженных деталей во время работы. В зависимости от величины зазора степень относительного перемещения деталей, сопряженных свободной посадкой, может быть различной. Для вращения шпинделя фрезерного станка в подшипниках зазор должен быть меньшим и, следовательно, посадка более тугой, чем для посадки колец на фрезерную оправку.

Посадками с натягом, или неподвижными, называют посадки, при которых во время работы не должно происходить перемещения сопряженных деталей относительно друг друга. В зависимости от величины натяга степень свободы сопряженных деталей неподвижной посадки может быть различной. Так, посадку шейки вала в кольцо шарикоподшипника производят с меньшим натягом, чем посадку колеса железнодорожного вагона на шейку оси.

При

переходных посадках возможно получение, как натягов, так и зазоров. При наибольшем предельном размере бруска и наименьшем предельном размере паза получается натяг, а при наименьшем предельном размере бруска и наибольшем предельном размере паза получается зазор (в таблицах допусков в графе «натяг» обозначен знаком минус).

Ниже приводятся посадки, относящиеся к рассмотренным трем группам; в скобках даются их сокращенные обозначения.

Наибольший натяг получается при горячей посадке, меньший — при прессовых посадках; наименьший зазор получается при скользящей посадке, немного больший — при посадке движения, почти втрое больший при ходовой, затем еще больший при легкоходовой и, наконец, наибольший при широкоходовой посадке.

При глухой, тугой, напряженной и плотной посадках, как указывалось выше, возможны натяги и зазоры в зависимости от получающихся отклонений размера.

Классы точности.

Точность изготовления характеризуется величиной допускаемых отклонений от заданных размеров и формы. Для разных машин требуются детали с различной точностью обработки. Очевидно, что детали плуга, дорожного катка и других сельскохозяйственных и дорожных машин могут быть изготовлены менее точно, чем детали фрезерного станка, а детали фрезерного станка требуют меньшей точности, чем детали измерительного прибора. В связи с этим в машиностроении детали разных машин изготовляют по разным классам точности. В СССР (были) приняты десять классов точности.

пять из них: 1-й, 2-й, 2а, 3-й, За — требуют наибольшей точности обработки;
два других: 4-й и 5-й — меньшей;
три остальных: 7-й, 8-й, 9-й — еще меньшей.

Применение классов точности в различных областях

1-й класс точности применяют при изготовлении особо точных изделий. Вследствие очень малых допусков работа по 1-му классу точности требует высокой квалификации рабочего и точного оборудования, приспособлений и инструмента.
2-й и 2а классы точности применяют наиболее часто. По ним изготовляют ответственные детали станков, автомобильных, тракторных, авиационных и электрических двигателей, текстильных и других машин.Наряду с этим в отраслях машиностроения, выпускающих указанные машины, детали менее ответственных соединений изготовляют по 3-му, 4-му, 5-му и другим более грубым классам точности.
3-й и За классы точности применяют главным образом в тяжелом машиностроении при производстве турбин, паровых машин, двигателей внутреннего сгорания, трансмиссионных деталей и т. д.
По 4-му классу точности изготовляют детали сельскохозяйственных машин, паровозов, железнодорожных вагонов и т. д.
5-й класс точности применяют в машиностроении для неответственных деталей менее точных механизмов.
7-й, 8-й и 9-й классы точности применяют при изготовлении более грубых деталей и особенно при заготовительных операциях: литье, штамповке, медницко-слесарных работах и т. д.
Свободные размеры деталей выполняют обычно по 5-му или 7-му классам точности.

Чтобы показать, с какой посадкой и по какому классу точности нужно изготовить деталь, в чертежах на номинальных сопрягаемых размерах ставится буква, обозначающая посадку, и цифра, соответствующая классу точности. Например, С₄ означает: скользящая посадка 4-го класса точности; Х₃ — ходовая посадка 3-го класса точности и т. п. Для посадок 2-го класса точности (особенно широко распространенных) цифра 2 не ставится. Поэтому, если в чертеже на сопрягаемом размере рядом с буквой посадки нет цифры, то это значит, что деталь надо изготовить по 2-му классу точности. Например, Л означает легкоходовая посадка 2-го класса точности.

Автор: С. В. Аврутин
Источник: Основы фрезерного дела, С. В. Аврутин, 1962г
Дата в источнике: 1962г

Особенности резьбонарезания, точность резьбы | stamo-tools.ru

Силы, действующие при резьбонарезании

Ниже приведены силы возникающие при резьбонарезании у метчика со спиральной канавкой (рис. А) и с прямой канавкой с подточкой (рис. Б):

Направление вращения

Силы резания

Осевые силы

Радиальные силы

рис. А (силы, действующие при использовании метчиков с правой спиралью)

рис. Б (силы, действующие при использовании метчиков со спиральным забрным конусом)

Это необходимо учесть при использовании плавающих резьбонарезных патронов.

В случае использования метчиков с правой спиралью осевые силы направлены в сторону подачи, что компенсируется продольным растяжением патрона. Это может привести к увеличенному шагу резьбы.

Поэтому значение подачи необходимо назначать приблизительно на 5% меньше от расчетной Vf= n*p (где n частота вращения, p-шаг резьбы).

В случае использования метчиков с левой спиралью или прямыми канавками осевые силы действуют против направления подачи, поэтому рекомендуется использовать расчетное значение подачи.

Точность резьбы

Метчик			Внутренняя резьба, гайка					Тип соединения
ISO	DIN	ANSI/ASME	Внутренняя резьба, гайка					Тип соединения
ISO 1	4H	3B	4H	5H				C натягом
ISO 2	6H	2B	4G	5G	6H			По переходной посадке
ISO 3	6G	1B			6G	7H	8H	С зазором
	7G					7G	8G	Прослабленное под покрытие

Классы точности

Внутренняя резьба

класс точности H

Допуски на метчики

Допуски на раскатники

Внутренняя резьба

класс G

D2 – средний диаметр, Au- основное отклонение

Для получения стандартного резьбового соединения с переходной посадкой необходимо использовать метчики с допуском ISO 2, 6H или 2В. Метчики с меньшим допуском по ISO 1 (4Н или 3В) позволяют получить соединение с натягом по среднему диаметру резьбы. Метчики с допуском по ISO 3 (6G, 1B) используются в гайках, на которые предполагается нанести покрытие.

Кроме метчиков с допусками 6H, 6G и 7G выпускаются метчики 6HX и 6GX. Буква “X” означает, что данный допуск не является стандартным. Такие метчики применяются в материалах для компенсации эластичной деформации материала. Поле допуска 6H и 6HX одно и то же. Используется такой вид допуска, как правило, в раскатниках.

Допуски на метрическую резьбу по стандарту ISO

Внутренняя резьба
Au	Основное отклонение
D	Диаметр впадин внутренней резьбы
D1	Диаметр вершин внутренней резьбы
D2	Средний диаметр
H	Высота исходного треугольника
P	Шаг
Td1	Допуск D1
Td2	Допуск D2
a	Угол профиля

Метчик
d	Диаметр впадин внутренней резьбы (=D)
d min	Диаметр впадин резьбы метчика
d2	Средний диаметр
d2 max	Максимальный средний диаметр
d2 min	Минимальный средний диаметр
E1	Нижнее отклонение d2
Es	Верхнее отклонение d2
E1d	Нижнее отклонение d
P	Шаг
R	Радиус впадины метчика
Td2	Допуск на средний диаметр
Ta2	Допуск половины угла профиля
a	Угол профиля
a/2	Половина угла профиля

	Внутренняя резьба
	Метчик

Что такое класс точности манометра — Автомастерская Adrenaline Garage Солонцы

Манометры выпускаются следующих классов точности: 0,6; 1; 1,5; 2,5; 4 (цифры расположены в порядке уменьшения значения класса точности приборов).

Класс точности – это максимально допустимая относительная погрешность прибора, приведенная к диапазону его шкалы, выраженная в процентах. Чем ниже значение класса точности тем меньше погрешность манометра.

Согласно ГОСТ 2405-88 класс точности приборов должен выбираться из ряда: 0,4; 0,6; 1,0; 1,5; 2,5; 4,0. В случае с дифференцированным значением основной погрешности устанавливают следующие условные обозначения классов точности: 0,6-0,4-0,6; 1-0,6-1; 1,5-1-1,5; 2,5-1,5-2,5; 4-2,5-4.

Обозначение класса точности	Предел допускаемой основной погрешности, % диапазона показаний, в диапазоне шкалы
Обозначение класса точности	от 0 до 25%	от 25 до 75%	св. 75 до 100%
0,4	±0,4	±0,4*	±0,4
0,6-0,4-0,6	±0,6	±0,4	±0,6
0,6	±0,6	±0,6	±0,6
1-0,6-1	±1,0	±0,6	±1,0
1	±1,0	±1,0	±1,0
1,5-1-1,5	±1,5	±1,0	±1,5
1,5	±1,5	±1,5	±1,5
2,5-1,5-2,5	±2,5	±1,5	±2,5
2,5	±2,5	±2,5	±2,5
4-2,5-4	±4,0	±2,5	±4,0
4	±4,0	±4,0	±4,0

Классом точности называют выраженную в процентах максимально допустимую погрешность манометра, приведенную к его диапазону измерений.

Чем ниже значение класса точности, тем меньше погрешность измерительного прибора.

Какие существуют классы точности

Согласно ГОСТ 2405-88 класс точности манометра должен выбираться из ряда чисел:

0,4;
0,6;
1,0;
1,5;
2,5;
4,0.

Как связаны диаметр и класс точности

Диаметр и класс точности манометра параметры взаимосвязанные, чем выше точность прибора для измерения давления, тем больше диаметр его шкалы.

Связь диаметра и класса точности манометра

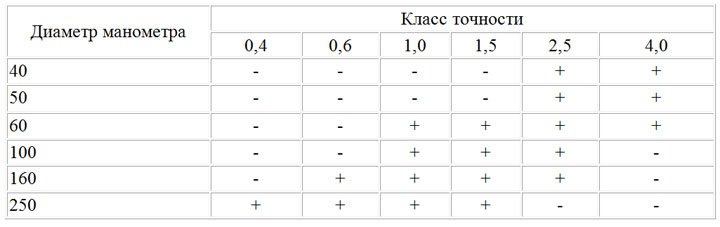
Какая погрешность у манометра с классом точности 1,5

Погрешность измерения манометра, зависит не только от его класса точности, но и от диапазона измерений.

Рассмотрим пример, диапазон измерения манометра составляет 10 МПа, класс точности прибора 1,5. Это означает, что максимальная погрешность манометра не должна превышать 10*1,5/100=0,15 МПа.

Манометр класса точности 2,5

Обозначение 2,5 означает, что максимально допустимая погрешность измерений манометра составляет 2,5% от его диапазона измерений.

Как узнать класс точности манометра

Класс точности указывается на шкале прибора, перед числовым значением могут располагаться буквы KL или CL.

Вычисление класса точности прибора

Предположим, что на шкале указан класс точности 1,0, а диапазон измерения прибора 250 Bar. При сравнении результатов измерения давления с показаниями образцового манометра выяснилось, что погрешность составляет 2 Bar. Соответствует ли манометр указанному классу точности?

Для того, чтобы ответить на этот вопрос произведем вычисление класса точности, для этого соотнесем погрешность измерений с диапазоном измерения прибора и выразим результат в процентах.

2*100/250=0,8

Полученный результат не превышает 1, это означает, что манометр соответствует указанному классу точности 1,0.

Классы точности весового оборудования – ЮУВЗ

Главным показателем качества весового оборудования прежде всего является его точность. Для каждого средства измерений устанавливается класс точности, что отражает их метрологические свойства, соответствующие требованиям техники и безопасности.

Метрологические характеристики – характеристики свойств измерительных приборов, которые оказывают влияние на конечный результат и в большей степени определяют погрешность прибора. Эти характеристики устанавливаются в соответствие с нормативно-техническими документами. Установленные этими документами характеристики называются нормируемыми, а когда их определяют экспериментальным путем, становятся – действительными. Правила выбора комплексов нормируемых метрологических характеристик для измерительных средств и способы их нормирования определены стандартом ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений». К основным характеристикам измерительных приборов относят: основную и дополнительную погрешность.

Существуют определенные классы точности и пределы допустимых погрешностей, прописанные в государственных стандартах. На сегодняшний день, для обозначения точности весового прибора используется ГОСТ OIML R 76-1-2011.

Согласно международным рекомендациям OIML класс точности подразделяется на 3 класса:

I-й специальный,
II-й высокий,
III-й средний.

Однако до 2001 года по ГОСТ 24104-1988 существовало 4 класса точности. Если сравнивать ГОСТы 1988 и 2001 и 2011 года, то в I-й(специальный) класс вошли 1 и 2 классы госта старой версии, а 3-4 класс в III-й средний. Также, отличаем новой версии стандарта следует считать появление новых характеристик: цена поверочного деления «е» и число поверочных делений «n». Пользуясь именно этими характеристиками, каждый специалист гарантированно может выбрать для себя те весы, которые подходят именно для выбранных задач. К тому же, из стандарта было исключено деление весов на общего назначения и образцовые, и деление по разрядам и классам точности I/1 – IV/4.

Классы точности присваивают при разработке по результатам государственных приемочных испытаний. При определении класса точности нормируют пределы допускаемой основной погрешности. Для промышленных весов, взвешивающих многотонные грузы, раньше использовался ГОСТ 29329-92 Весы для статического взвешивания. Сейчас же, все весовые производители(Южно-Уральский Весовой Завод не исключение), используют ГОСТ OIML R 76-1-2011.

Формы выражения пределов погрешностей

Пределы погрешностей могут быть выражены в форме абсолютной, приведенной или относительной погрешности. Форма выражения погрешности для измерительных средств определяется в соответствии с их видом, свойствами, принципом действия, назначением и других факторов, влияющих на характер погрешности.

Параметры точности и погрешности весов

В весоизмерительных оборудованиях существует наибольший(НПВ) и наименьший(НМПВ) предел взвешивания весов. Наибольший предел взвешивания – это верхняя граница предела взвешивания. НПВ определяет самую большую массу при взвешивании на весах за один раз. Наименьший предел взвешивания – это нижняя граница предела взвешивания. НМПВ определяет какой наименьший вес можно взвесить на весах с допустимой степенью погрешности.

Цена деления весов

Предельно допустимая погрешность у весов обозначается величиной «e», ее еще называют «цена поверочного деления». Предельно допустимая погрешность должна быть не более определенной по нормативным документам. Она указывается заводом изготовителем при производстве весов. Дискретность – это значение, изменяющееся между несколькими различными стабильными состояниями. В качестве примера можно привести механические часы, в которых минутная стрелка перемещается скачкообразно, т.е. дискретно, на одну шестидесятую целой окружности циферблата. Дискретность обозначается как «d». Предельно допустимая погрешность весов определяется ценой поверочного деления e. Производители весов и весового оборудования весов гарантирует следующее соотношение: d = e. Чем ниже погрешность на весах, тем выше точность измерений весового прибора. Погрешность весов в диапазоне измерений по абсолютному значению не должна превышать пределов допускаемой погрешности.

Пределы допускаемой погрешности

Для нагрузки (m),выраженной в поверочных интервалах весов			Пределы допускаемой погрешности
I класс точности (специальный)	II класс точности (высокий)	III класс точноcти (средний)	Первичная проверка	В эксплуатации
0 ≤ m ≤ 50000 e	0 ≤ m≤5000 e	0 ≤ m≤500 e	± 0,5 e	± 1 e
50000 e < m ≤ 200000 e	5000 e < m ≤ 20000 e	500 e < m ≤ 2000 e	± 1,0 e	± 2 e
20000 e < m	20000 e < m ≤ 100000	2000 e < m ≤ 10000	± 1,5 e	± 3 e

Промышленные весы, взвешивающие большие многотонные грузы, производства Южно-Уральского Весового Завода такие как автомобильные, вагонные, платформенные и др. используется III (средний) класс точности.

Другие факторы, влияющие на погрешность измерения весов

Существует великое множество факторов, влияющих на погрешность измерения весоизмерительного оборудования. Очень сложно, если не невозможно, точно измерить вес объекта. Влияет буквально все – погодные условия (температура, влажность), человеческий фактор и др. Механические весы страдают от естественного стачивания трущихся деталей механизма. А также прочие факторы, влияющих на погрешность при взвешивании. Именно поэтому, производители весов ставят в приоритет задачи по сведению к минимуму погрешности измерения веса, для долгого срока службы весов.

В Российской Федерации средства измерений должны соответствовать условиям эксплуатации и установленным требованиям. На средство взвешивания обязательно оформляется сертификат об утверждении типа средства взвешивания.

Класс точности – это… Что такое Класс точности?

Класс точности — основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.

Погрешность может нормироваться, в частности, по отношению к:

результату измерения (по относительной погрешности)

в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.

длине (верхнему пределу) шкалы прибора (по приведенной погрешности)

Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.

Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.

Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Следует иметь в виду, что понятие класса точности встречается в различных областях техники. Так в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков (по ГОСТ 20551).

Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.

Аппараты с классом точности 0,5 (0,2) начинают работать в классе от 5 % загрузки. а 0,5s (0,2s) уже с 1 % загрузки

См. также

Ссылки

Класс точности — Карта знаний

Класс точности — обобщённая характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений.
Погрешность может нормироваться, в частности, по отношению к:
результату измерения (по относительной погрешности)в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.длине (верхнему пределу) шкалы прибора (по приведенной погрешности).Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0—30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В.
Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1—0,5 В.
Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
Следует иметь в виду, что понятие класса точности встречается в различных областях техники. Так, в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков (по ГОСТ 20551).
Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.
Аппараты с классом точности 0,5 (0,2) проходят метрологические испытания с 5 % загрузки, а 0,5s (0,2s) уже с 1 % загрузки.

Источник: Википедия

Связанные понятия

Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения. Параметр — это обобщенное название определенного физического, геометрического или иного свойства устройства (процесса). Это могут быть, например, размер, скорость, напряжение и т. д. Градуиро́вка (нем. graduiren «градуировать» от лат. gradus «шаг, ступень, степень») средств измерений, иногда тари́рование — метрологическая операция, при помощи которой средство измерений (меру или измерительный прибор) снабжают шкалой или градуировочной таблицей (кривой). Отметки шкалы должны с требуемой точностью соответствовать значениям измеряемой величины, а таблица (кривая) с требуемой точностью отражать связь эффекта на выходе прибора с величиной, подводимой ко входу (например, зависимость… Измери́тельный прибо́р — средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне. Часто измерительным прибором называют средство измерений для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия оператора. Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).

Упоминания в литературе

Излучатели профилографов можно ориентировать как вверх, так и вниз. Задаваемая толщина слоев лимитируется необходимой точностью измерения (табл. 5). По классу точности датчика температуры данные профилографы относятся к ненормируемым, что оправдано, поскольку данный параметр выступает как вспомогательный. По классу точности датчика давления они относятся к высшему классу точности (табл. 1). Кроме интерфейса типа RS232 (RS232C) профилографы течений также имеют интерфейс типа RS422. Передача данных производится со скоростью 9600–115 400 бод. Если на предприятии нет самопишущих вольтметров, записи напряжения производятся по лабораторным стрелочным приборам класса точности 0,5-1,5, подключаемым к шинам низкого напряжения непосредственно или через трансформаторы напряжения класса точности 0,5. На вводах высокого напряжения лабораторные вольтметры включаются во вторичную обмотку трансформаторов напряжения. При отсутствии самопишущих и лабораторных стрелочных вольтметров напряжение записывается по щитовым вольтметрам. Вольтметры, по которым составляются графики напряжения, должны быть исправны, и проверены госповерителем.

Связанные понятия (продолжение)

Мнимая точность, также ложная, кажущаяся, избыточная то́чность (англ. spurious accuracy) — ошибка мнения о точности данных, возникающая на основании представления данных в более точном виде, чем известно об их точности. Компара́тор — это техническое средство, естественные или специально создаваемые среды, позволяющие сличать друг с другом меры однородных величин или показания измерительных приборов, а также сравнивать участки (точки) шкал измерений. Шкала́ (лат. scala — лестница) — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией или техническая отметка на шкале измерительного прибора. Шкалы могут располагаться по окружности, дуге или прямой линии. Показания отсчитываются невооружённым глазом при расстояниях между делениями до 0,7 мм, при меньших — при помощи лупы или микроскопа, для долевой оценки делений применяют дополнительные шкалы — нониусы. До́пуск — разность между наибольшим и наименьшим предельными значениями параметров (размеров, массовой доли, массы), задаётся на геометрические размеры деталей, механические, физические и химические свойства. Назначается (выбирается) исходя из технологической точности или требований к изделию (продукту). Любое значение параметра, оказывающееся в заданном интервале, является допустимым. Измеритель уровня звука — измерительный прибор, применяемый в звукотехнике для определения уровня звукового сигнала. Звук измеряется в децибелах (дБ). Это логарифмические единицы, которые хорошо отражают характеристику слуха, поскольку слух человека ощущает только относительные изменения акустического давления. Но́ниус (шкала́-но́ниус, шкала́ Но́ниуса, вернье́р) — вспомогательная шкала, устанавливаемая на различных измерительных приборах и инструментах, служащая для более точного определения количества долей делений основной шкалы. Преобразова́ние едини́ц — перевод физической величины, выраженной в одной системе единиц, в другую систему, обычно через коэффициент пересчёта. Номогра́мма (от др.-греч. νόμος — закон и γράμμα — письмо) — графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывания линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул. Округление — замена числа на его приближённое значение (с определённой точностью), записанное с меньшим количеством значащих цифр. Модуль разности между заменяемым и заменяющим числом называется ошибкой округления. Метод парных точек — метод обработки экспериментальных данных, созданный для оценивания значения углового коэффициента зависимости и определения его погрешности. Из экспериментальных точек на графике берутся те, которые находятся друг от друга примерно на одинаковом расстоянии (это расстояние должно быть максимально возможным). Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Математически распределение частот является функцией, которая в первую очередь определяет для каждого показателя идеальное значение, так как эта величина обычно уже измерена. Такое распределение можно представить в виде таблицы или графика, моделируя функциональные уравнения. В описательной статистике частота распределения имеет ряд математических функций, которые используются для выравнивания… Светочувствительность цифровой фотокамеры — характеристика цифрового фотоаппарата, определяющая зависимость числовых параметров созданного им цифрового изображения от экспозиции, полученной светочувствительной матрицей. Светочувствительность цифровых фотоаппаратов принято выражать в единицах, эквивалентных светочувствительности ISO желатиносеребряных фотоэмульсий. Это позволяет пользоваться методами измерения экспозиции, свойственными классической плёночной фотографии. Твёрдость по Шору обозначается в виде числового значения шкалы, к которому приписывается буква, указывающая тип шкалы с явным указанием названия метода измерения твердости или прибора. Например… Твёрдость — свойство материала сопротивляться внедрению более твёрдого тела — индентора. Предел обнаружения в химическом анализе — минимальное содержание определяемого вещества в пробе, сигнал от которого можно надёжно отличить от фона. Обычно предел обнаружения принимают равным утроенному значению стандартного отклонения шумового сигнала. Иными словами сигнал, равный или превышающий уровень сигнала, установленный для предела обнаружения, с вероятностью более 99 % означает, что он относится к искомому компоненту. Измери́тельный мост (мост Уи́тстона, мо́стик Ви́тстона, англ. Wheatstone bridge) — электрическая схема или устройство для измерения электрического сопротивления. Предложен в 1833 году Самуэлем Хантером Кристи (англ. Samuel Hunter Christie) и в 1843 году усовершенствован Чарльзом Уитстоном (англ. Charles Wheatstone). Мост Уитстона относится к одинарным мостам в отличие от двойных мостов Томсона. Мост Уитстона — электрическое устройство, механическим аналогом которого являются аптекарские рычажные… Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых…

Подробнее: Критерий Уилкоксона

Винеровское оценивание — задача нахождения импульсной характеристики линейной стационарной системы, дающей на выходе оптимальную в смысле минимума математического ожидания средней квадратической ошибки оценку значений полезного сигнала, поступающего на вход в аддитивной смеси с шумом. Наземный лазерный сканер (НЛС) — это съёмочная система, измеряющая с высокой скоростью (от нескольких тысяч до миллиона точек в секунду) расстояния от сканера до поверхности объекта и регистрирующая соответствующие направления (вертикальные и горизонтальные углы) с последующим формированием трёхмерного изображения (скана) в виде облака точек.

Подробнее: Наземное лазерное сканирование

Число Штреля (англ. Strehl ratio) — величина, характеризующая качество оптического изображения, впервые предложенная Карлом Штрелем и названная в честь него. Используется в ситуациях, когда оптическое разрешение ухудшается из-за аберраций в линзе или из-за искажений при прохождении через турбулентную атмосферу. Имеет значение от 0 до 1, при этом в гипотетической идеальной оптической системе число Штреля равно 1. Экспозиционное число, экспозиционный канал (англ. Exposure Value, EV) — условное целое число, однозначно характеризующее экспозицию при фото- и киносъёмке. Одному и тому же экспозиционному числу могут соответствовать различные комбинации выдержки и диафрагмы (экспопары), но одно и то же количество света. В соответствии с законом взаимозаместимости эти сочетания по действию на светочувствительный материал равнозначны и соответствуют одному и тому же экспозиционному числу. При этом, экспозиционное… Модель сейсмического воздействия «СА-482» — совокупность универсальных характеристик, предназначенных для расчётов сейсмостойкости наземных объектов, состоящая из обобщённых спектров коэффициента динамичности (СКД) и синтезированной акселерограммы (СА-482). Анализ размерности (чаще говорят «соображения размерности» или «метрические соображения») — инструмент, используемый в физике, химии, технике и нескольких направлениях экономики для построения обоснованных гипотез о взаимосвязи различных параметров сложной системы. Неоднократно применялся физиками на интуитивном уровне не позже XIX века. Доплеровский измеритель скорости и сноса (ДИСС) — бортовое радиолокационное устройство, основанное на использовании эффекта Доплера, предназначенное для автоматического непрерывного измерения и индикации составляющих вектора скорости, модуля путевой скорости, угла сноса и координат летательного аппарата, автономно или в комплексе с навигационным оборудованием. Физи́ческая величина́ — измеряемое качество, признак или свойство материального объекта или явления, общее в качественном отношении для класса материальных объектов или процессов, явлений, но в количественном отношении индивидуальное для каждого из них. Физические величины имеют род, размер, единицу(измерения) и значение. Коэффициент стоячей волны (КСВ, от англ. standing wave ratio, SWR) — отношение наибольшего значения амплитуды напряжённости электрического или магнитного поля стоячей волны в линии передачи к наименьшему. Пара́метр (от др.-греч. παραμετρέω — «отмеривающий»; где παρά: «рядом», «второстепенный», «вспомогательный», «подчинённый»; и μέτρον: «измерение») — величина, значения которой служат для различения элементов некоторого множества между собой.. Параметр – величина, постоянная в пределах данного явления или задачи, но при переходе к другому явлению или задаче могущая изменить своё значение. Иногда параметрами называют также величины, очень медленно изменяющиеся по сравнению с другими величинами (переменными… Складной нож (англ. jackknife) — один из методов ресэмплинга (линейное приближением статистического бутстрэпа), используемый для оценки погрешности в статистическом выводе. Способ заключается в следующем: для каждого элемента вычисляется среднее значение выборки без учёта данного элемента, а затем — среднее всех таких значений. Для выборки из N элементов оценка получается путём вычисления среднего значения остальных N-1 элементов. Чувстви́тельность — способность объекта реагировать определённым образом на определённое малое воздействие, а также количественная характеристика этой способности. Измери́тель нелине́йных искаже́ний, ИНИ, (измеритель коэффициента гармоник) — прибор для измерения коэффициента нелинейных искажений, КНИ (коэффициента гармоник) сигналов в радиотехнических и электронных устройствах. Ме́тод Рокве́лла — метод неразрушающей проверки твёрдости материалов. Основан на измерении глубины проникновения твёрдого наконечника индентора в исследуемый материал при приложении одинаковой для каждой шкалы твердости нагрузкой, в зависимости от шкалы обычно 60, 100 и 150 кгс. Многочасти́чный фильтр (МЧФ, англ. particle filter — «фильтр частиц», «частичный фильтр», «корпускулярный фильтр») — последовательный метод Монте-Карло — рекурсивный алгоритм для численного решения проблем оценивания (фильтрации, сглаживания), особенно для нелинейных и не-гауссовских случаев. Со времени описания в 1993 году Н. Гордоном, Д. Салмондом и А. Смитом используется в различных областях — навигации, робототехнике, компьютерном зрении. Фи́льтр Ка́лмана — эффективный рекурсивный фильтр, оценивающий вектор состояния динамической системы, используя ряд неполных и зашумленных измерений. Назван в честь Рудольфа Калмана. Задача характеризации элементов микросхем заключается в получении зависимостей функциональных параметров библиотечного элемента или блока от длительности фронтов сигналов на входе и от величины нагрузочных емкостей для заданных наборов этих величин. В коммерческих системах характеризации (SiliconSmart , Virtuoso Liberate Characterization Solution , Virtuoso Variety Statistical Characterization Solution , Virtuoso Liberate MX Memory Characterization Solution , Kronos Characterizer Plus ) такие зависимости… Кориолисовы расходомеры — приборы, использующие эффект Кориолиса для измерения массового расхода жидкостей, газов. Принцип действия основан на изменениях фаз механических колебаний U-образных трубок, по которым движется среда. Сдвиг фаз пропорционален величине массового расхода. Поток с определенной массой, движущийся через входные ветви расходомерных трубок, создает кориолисову силу, которая сопротивляется колебаниям расходомерных трубок. Наглядно это сопротивление чувствуется, когда гибкий шланг…

Подробнее: Кориолисов расходомер

Виды измерений — области измерений, выделяемые по одному из классифицирующих признаков. Рассматриваются в метрологии. Канде́ла (от лат. candela — свеча; русское обозначение: кд; международное: cd) — единица силы света, одна из семи основных единиц Международной системы единиц (СИ). Определена как «сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540⋅1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср». Принята в качестве единицы СИ в 1979 году XVI Генеральной конференцией по мерам и весам. Весы́ — устройство или прибор для определения массы тел (взвешивания) по действующему на них весу, приближённо считая его равным силе тяжести. Вес тела может быть определён как через сравнение с весом эталонной массы (как в рычажных весах), так и через измерение этой силы через другие физические величины. Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала. Иногда эту характеристику называют «частотным откликом системы» (frequency response). Штрихова́я ме́ра длины́ — мера, представляющая одно или несколько значений длины, определённых кратчайшим расстоянием между центрами двух штрихов шкалы меры. Штриховые меры длины применяются как эталонные меры для передачи размера единицы длины мерам меньшей точности, для калибровки средств измерений длины и линейных измерительных преобразователей, как рабочие меры для регулировки средств измерений длины и станков, для прямых измерений длины и линейных перемещений в станках и приборах. Логарифмический масштаб (шкала) — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах. Установка для поверки расходомеров представляет собой достаточно сложное техническое устройство, обеспечивающее воспроизведение потока жидкости с расходом от 10 — 20 до 600000 литров в час (0,01 — 600 м³/ч) и измерение объема (массы) эталонными расходомерами или весовым устройством с необходимой для поверки точностью. Установка относится к средствам измерения, для которых установлена своя система сертификации (утверждение типа и внесение в Государственный реестр) и подтверждение пригодности для использования… Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования…

Подробнее: ПИД-регулятор

90000 Accuracy Class C H P Linear Guide Rail With Competitive Price 90001 90002 90003 accuracy class CHP linear guide rail with competitive price 90004 90005 90002 accuracy class CHP linear guide rail with competitive price 90005 90002 accuracy class CHP linear guide rail with competitive price 90005 90002 90005 90002 Product Description 90005 90002 90003 Feature of Linear Guide Rail 90004 90005 90018 90019 Cost reduction 90020 90019 Clean and environmentally friendly 90020 90019 Long last and low maintenance 90020 90019 No installed limitations 90020 90019 Easy to be assembled and dismantled 90020 90019 Different oils can be selected 90020 90031 90002 90005 90002 90003 Pictures of Linear Guide Rail 90004 90005 90002 90005 90002 90005 90002 90005 90002 90005 90002 90003 Specification of Linear Guide Rail: 90004 90005 90002 90005 90002 90005 90002 90003 Model number of linear motion guideway: 90004 90005 90002 90005 90002 90005 90002 HGh25CA HGh30CA HGh30HA HGh35CA HGh35HA H Gh40CA HGh40HA HGh45CA HGh45HA HGh55CA HGh55HA HGH55CA HGH55HA HGH65CA HGH65HA 90005 90002 90005 90002 HGW15CA HGW20CA HGW20HA HGW25CA HGW25HA HGW30CA HGW30HA HGW35CA HGW35HA HGW45CA HGW45HA HGW55CA HGW55HA HGW65CA HGW65HA 90005 90002 90005 90002 HGW15CB HGW20CB HGW20HB HGW25CB HGW25HB HGW30CB HGW30HB HGW35CB 90005 90002 HGW35HB HGW45CB HGW45HB HGW55CB HGW55HB HGW65CB HGW65HB 90005 90002 90005 90002 HGW15CC HGW20CC HGW20HC HGW25CC HGW25HC HGW30CC HGW30HC HGW35CC HGW35HC HGW45CC HGW45HC HGW55CC HGW55HC HGW65CC HGW65HC 90005 90002 90005 90002 EGh25SA EGh25CA EGh30SA EGh30CA EGh35SA EGh35CA EGh40SA EGh40CA 90005 90002 90083 EGW15SA EGW15CA EGW20SA EGW20CA EGW25SA EGW30SA EGW30CA 90005 90002 90083 EGW15SB EGW15CB EGW20SB EGW20CB EGW25SB EGW25CB EGW30SB EGW30CB 90005 90002 90005 90002 MGN7C MGN9C MGN12C MGN15C MGW7C MGW9C MGW12C MGW15C MGN7H MGN9H MGN12H 90005 90002 90005 90002 90003 Installation Drawing 🙁 just for reference) 90004 90005 90002 90005 90002 90003 90004 90005 90002 90005 90002 90005 90002 90003 For more product information, you can click the following 90004 90005 90002 90003 picture.90004 90005 90002 90005 90002 90005 90002 90005 90002 90003 Application of linear guideway: 90004 90005 90002 90005 90018 90019 1.Machining center 90020 90019 2.Machine tools, 90020 90019 3.Precision processing 90020 90019 4.Heavy cutting tools, 90020 90019 5. Marble cutting machine 90020 90019 6.grinder 90020 90019 7.Injection machine 90020 90019 8.punch 90020 90019 9.Automation devices 90020 90031 90002 90005 90002 90005 90002 Packaging & Shipping 90005 90002 90005 90002 90005 90158 90005 90160 90005 90160 90005 90002 90005 90002 90005 90168 90005 90002 FAQ 90005 90002 90005 90002 90005 90002 90005 90168 90003 Welcome to inquiry us! 90004 90005 90168 accuracy class C H P linear guide rail with competitive price 90005 90168 accuracy class C H P linear guide rail with competitive price 90005 90168 90005 .90000 Evaluation of Classification Model Accuracy: Essentials – Articles 90001 90002 After building a predictive classification model, you need to 90003 evaluate the performance of the model 90004, that is how good the model is in predicting the outcome of new observations test data that have been not used to train the model. 90005 90002 In other words you need to estimate the model prediction 90007 accuracy 90008 and prediction errors using a new test data set. Because we know the actual outcome of observations in the test data set, the performance of the predictive model can be assessed by comparing the predicted outcome values against the known outcome values.90005 90002 This chapter describes the commonly used metrics and methods for assessing the performance of predictive classification models, including: 90005 90012 90013 90003 Average classification accuracy 90004, representing the proportion of correctly classified observations. 90016 90013 90003 Confusion matrix 90004, which is 2×2 table showing four parameters, including the number of true positives, true negatives, false negatives and false positives. 90016 90013 90003 Precision, Recall and Specificity 90004, which are three major performance metrics describing a predictive classification model 90016 90013 90003 ROC curve 90004, which is a graphical summary of the overall performance of the model, showing the proportion of true positives and false positives at all possible values of probability cutoff.The 90003 Area Under the Curve 90004 (90003 AUC 90004) summarizes the overall performance of the classifier. 90016 90033 90002 We’ll provide practical examples in R to compute these above metrics, as well as, to create the ROC plot. 90005 90002 Contents: 90005 90038 90002 The Book: 90005 90038 Machine Learning Essentials: Practical Guide in R 90042 Loading required R packages 90043 90012 90013 90046 tidyverse 90047 for easy data manipulation and visualization 90016 90013 90046 caret 90047 for easy machine learning workflow 90016 90033 90054 90046 library (tidyverse) library (caret) 90047 90057 90042 Building a classification model 90043 90002 To keep things simple, we’ll perform a binary classification, where the outcome variable can have only two possible values: negative vs positive.90005 90002 We’ll compute an example of linear discriminant analysis model using the 90046 PimaIndiansDiabetes2 90047 [mlbench package], introduced in Chapter @ref (classification-in-r), for predicting the probability of diabetes test positivity based on clinical variables. 90005 90066 90013 Split the data into training (80%, used to build the model) and test set (20%, used to evaluate the model performance): 90016 90069 90054 90046 # Load the data data ( “PimaIndiansDiabetes2”, package = “mlbench”) pima.data% createDataPartition (p = 0.8, list = FALSE) train.data 90047 90057 90074 90013 Fit the LDA model on the training set and make predictions on the test data: 90016 90069 90054 90046 library (MASS) # Fit LDA fit 90047 90057 90042 Overall classification accuracy 90043 90002 The overall 90003 classification accuracy 90004 rate corresponds to the proportion of observations that have been correctly classified. Determining the raw classification accuracy is the first step in assessing the performance of a model.90005 90002 Inversely, the 90003 classification error rate 90004 is defined as the proportion of observations that have been misclassified. 90046 Error rate = 1 – accuracy 90047 90005 90002 The raw classification accuracy and error can be easily computed by comparing the observed classes in the test data against the predicted classes by the model: 90005 90054 90046 accuracy 90047 90057 90054 90046 ## [1] 0.808 90047 90057 90054 90046 error 90047 90057 90054 90046 ## [1] 0.192 90047 90057 90002 From the output above, the linear discriminant analysis correctly predicted the individual outcome in 81% of the cases. This is by far better than random guessing. The misclassification error rate can be calculated as 100 – 81% = 19%. 90005 90002 In our example, a binary classifier can make two types of errors: 90005 90012 90013 it can incorrectly assign an individual who is diabetes-positive to the diabetes-negative category 90016 90013 it can incorrectly assign an individual who is diabetes-negative to the diabetes-positive category.90016 90033 90002 The proportion of theses two types of errors can be determined by creating a 90003 confusion matrix 90004, which compare the predicted outcome values against the known outcome values. 90005 90042 Confusion matrix 90043 90002 The R function 90046 table () 90047 can be used to produce a 90003 confusion matrix 90004 in order to determine how many observations were correctly or incorrectly classified. It compares the observed and the predicted outcome values and shows the number of correct and incorrect predictions categorized by type of outcome.90005 90054 90046 # Confusion matrix, number of cases table (observed.classes, predicted.classes) 90047 90057 90054 90046 ## predicted.classes ## observed.classes neg pos ## neg 48 4 ## pos 11 15 90047 90057 90054 90046 # Confusion matrix, proportion of cases table (observed.classes, predicted.classes)%>% prop.table ()%>% round (digits = 3) 90047 90057 90054 90046 ## predicted.classes ## observed.classes neg pos ## neg 0.615 0.051 ## pos 0.141 0.192 90047 90057 90002 The diagonal elements of the confusion matrix indicate correct predictions, while the off-diagonals represent incorrect predictions. So, the correct classification rate is the sum of the number on the diagonal divided by the sample size in the test data. In our example, that is (48 + 15) / 78 = 81%. 90005 90002 Each cell of the table has an important meaning: 90005 90002 90005 90012 90013 90003 True positives 90004 (d): these are cases in which we predicted the individuals would be diabetes-positive and they were.90016 90013 90003 True negatives 90004 (a): We predicted diabetes-negative, and the individuals were diabetes-negative. 90016 90013 90003 False positives 90004 (b): We predicted diabetes-positive, but the individuals did not actually have diabetes. (Also known as a 90007 Type I error 90008.) 90016 90013 90003 False negatives 90004 (c): We predicted diabetes-negative, but they did have diabetes. (Also known as a 90007 Type II error 90008.) 90016 90033 90002 Technically the raw prediction accuracy of the model is defined as 90046 (TruePositives + TrueNegatives) / SampleSize 90047.90005 90042 Precision, Recall and Specificity 90043 90002 In addition to the raw classification accuracy, there are many other metrics that are widely used to examine the performance of a classification model, including: 90005 90002 90003 Precision 90004, which is the proportion of true positives among all the individuals that have been predicted to be diabetes-positive by the model. This represents the accuracy of a predicted positive outcome. 90046 Precision = TruePositives / (TruePositives + FalsePositives) 90047.90005 90002 90003 Sensitivity 90004 (or 90003 Recall 90004), which is the 90003 True Positive Rate 90004 (TPR) or the proportion of identified positives among the diabetes-positive population (class = 1). 90046 Sensitivity = TruePositives / (TruePositives + FalseNegatives) 90047. 90005 90002 90003 Specificity 90004, which measures the 90003 True Negative Rate 90004 (TNR), that is the proportion of identified negatives among the diabetes-negative population (class = 0). 90046 Specificity = TrueNegatives / (TrueNegatives + FalseNegatives) 90047.90005 90002 90003 False Positive Rate 90004 (FPR), which represents the proportion of identified positives among the healthy individuals (i.e. diabetes-negative). This can be seen as a false alarm. The FPR can be also calculated as 90046 1-specificity 90047. When positives are rare, the FPR can be high, leading to the situation where a predicted positive is most likely a negative. 90005 90002 90003 Sensitivy 90004 and 90003 Specificity 90004 are commonly used to measure the performance of a predictive model.90005 90002 These above mentioned metrics can be easily computed using the function 90046 confusionMatrix () 90047 [caret package]. 90005 90002 In two-class setting, you might need to specify the optional argument 90046 positive 90047, which is a character string for the factor level that corresponds to a “positive” result (if that makes sense for your data). If there are only two factor levels, the default is to use the first level as the “positive” result. 90005 90054 90046 confusionMatrix (predicted.classes, observed.classes, positive = “pos”) 90047 90057 90054 90046 ## Confusion Matrix and Statistics ## ## Reference ## Prediction neg pos ## neg 48 11 ## pos 4 15 ## ## Accuracy: 0.808 ## 95% CI: (0.703, 0.888) ## No Information Rate: 0.667 ## P-Value [Acc> NIR]: 0.00439 ## ## Kappa: 0.536 ## Mcnemar’s Test P-Value: 0.12134 ## ## Sensitivity: 0.577 ## Specificity: 0.923 ## Pos Pred Value: 0.789 ## Neg Pred Value: 0.814 ## Prevalence: 0.333 ## Detection Rate: 0.192 ## Detection Prevalence: 0.244 ## Balanced Accuracy: 0.750 ## ## ‘Positive’ Class: pos ## 90047 90057 90002 The above results show different statistical metrics among which the most important include: 90005 90012 90013 the cross-tabulation between prediction and reference known outcome 90016 90013 the model accuracy, 81% 90016 90013 the kappa (54%), which is the accuracy corrected for chance.90016 90033 90002 In our example, the sensitivity is ~ 58%, that is the proportion of diabetes-positive individuals that were correctly identified by the model as diabetes-positive. 90005 90002 The specificity of the model is ~ 92%, that is the proportion of diabetes-negative individuals that were correctly identified by the model as diabetes-negative. 90005 90002 The model precision or the proportion of positive predicted value is 79%. 90005 90002 In medical science, sensitivity and specificity are two important metrics that characterize the performance of classifier or screening test.The importance between sensitivity and specificity depends on the context. Generally, we are concerned with one of these metrics. 90005 90002 In medical diagnostic, such as in our example, we are likely to be more concerned with minimal wrong positive diagnosis. So, we are more concerned about high Specificity. Here, the model specificity is 92%, which is very good. 90005 90002 In some situations, we may be more concerned with tuning a model so that the sensitivity / precision is improved. To this end, you can test different probability cutoff to decide which individuals are positive and which are negative.90005 90002 Note that, here we have used 90046 p> 0.5 90047 as the probability threshold above which, we declare the concerned individuals as diabetes positive. However, if we are concerned about incorrectly predicting the diabetes-positive status for individuals who are truly positive, then we can consider lowering this threshold: 90046 p> 0.2 90047. 90005 90042 ROC curve 90043 90268 Introduction 90269 90002 The 90003 ROC curve 90004 (or 90003 receiver operating characteristics curve 90004) is a popular graphical measure for assessing the performance or the accuracy of a classifier, which corresponds to the total proportion of correctly classified observations.90005 90002 For example, the accuracy of a medical diagnostic test can be assessed by considering the two possible types of errors: false positives, and false negatives. In classification point of view, the test will be declared positive when the corresponding predicted probability, returned by the classifier algorithm, is above a fixed threshold. This threshold is generally set to 0.5 (i.e., 50%), which corresponds to the random guessing probability. 90005 90002 So, in reference to our diabetes data example, for a given fixed probability cutoff: 90005 90012 90013 the 90003 true positive rate 90004 (or fraction) is the proportion of identified positives among the diabetes-positive population.Recall that, this is also known as the 90003 sensitivity 90004 of the predictive classifier model. 90016 90013 and the 90003 false positive rate 90004 is the proportion of identified positives among the healthy (i.e. diabetes-negative) individuals. This is also defined as 90046 1-specificity 90047, where 90003 specificity 90004 measures the 90003 true negative rate 90004, that is the proportion of identified negatives among the diabetes-negative population. 90016 90033 90002 Since we do not usually know the probability cutoff in advance, the ROC curve is typically used to plot the true positive rate (or sensitivity on y-axis) against the false positive rate (or “1-specificity” on x-axis ) at all possible probability cutoffs.This shows the trade off between the rate at which you can correctly predict something with the rate of incorrectly predicting something. Another visual representation of the ROC plot is to simply display the sensitive against the specificity. 90005 90002 The 90003 Area Under the Curve 90004 (90003 AUC 90004) summarizes the overall performance of the classifier, over all possible probability cutoffs. It represents the ability of a classification algorithm to distinguish 1s from 0s (i.e, events from non-events or positives from negatives).90005 90002 For a good model, the ROC curve should rise steeply, indicating that the true positive rate (y-axis) increases faster than the false positive rate (x-axis) as the probability threshold decreases. 90005 90002 So, the “ideal point” is the top left corner of the graph, that is a false positive rate of zero, and a true positive rate of one. This is not very realistic, but it does mean that the larger the AUC the better the classifier. 90005 90002 The AUC metric varies between 0.50 (random classifier) and 1.00. Values above 0.80 is an indication of a good classifier. 90005 90002 In this section, we’ll show you how to compute and plot ROC curve in R for two-class and multiclass classification tasks. We’ll use the linear discriminant analysis to classify individuals into groups. 90005 90268 Computing and plotting ROC curve 90269 90002 The ROC analysis can be easily performed using the R package 90046 pROC 90047. 90005 90054 90046 library (pROC) # Compute roc res.roc 90047 90057 90002 90005 90002 The gray diagonal line represents a classifier no better than random chance. 90005 90002 A highly performant classifier will have an ROC that rises steeply to the top-left corner, that is it will correctly identify lots of positives without misclassifying lots of negatives as positives. 90005 90002 In our example, the AUC is 0.85, which is close to the maximum (max = 1). So, our classifier can be considered as very good. A classifier that performs no better than chance is expected to have an AUC of 0.5 when evaluated on an independent test set not used to train the model. 90005 90002 If we want a classifier model with a specificity of at least 60%, then the sensitivity is about 0.88%. The corresponding probability threshold can be extract as follow: 90005 90054 90046 # Extract some interesting results roc.data% filter (specificity> = 0.6) 90047 90057 90054 90046 ## # A tibble: 44 x 3 ## thresholds sensitivity specificity ## ## 1 0.111 0.885 0.615 ## 2 0.114 0.885 0.635 ## 3 0.114 0.885 0.654 ## 4 0.115 0.885 0.673 ## 5 0.119 0.885 0.692 ## 6 0.131 0.885 0.712 ## # … with 38 more rows 90047 90057 90002 The best threshold with the highest sum sensitivity + specificity can be printed as follow. There might be more than one threshold. 90005 90054 90046 plot.roc (res.roc, print.auc = TRUE, print.thres = “best”) 90047 90057 90002 90005 90002 Here, the best probability cutoff is 0.335 resulting to a predictive classifier with a specificity of 0.84 and a sensitivity of 0.660. 90005 90002 Note that, 90046 print.thres 90047 can be also a numeric vector containing a direct definition of the thresholds to display: 90005 90054 90046 plot.roc (res.roc, print.thres = c (0.3, 0.5, 0.7)) 90047 90057 90268 Multiple ROC curves 90269 90002 If you have grouping variables in your data, you might wish to create multiple ROC curves on the same plot. This can be done using ggplot2.90005 90054 90046 # Create some grouping variable glucose% filter (thresholds! = – Inf)%>% mutate (glucose = glucose, age = age) # Create ROC curve ggplot (roc.data, aes (specificity, sensitivity)) + geom_path (aes (color = age)) + scale_x_reverse (expand = c (0,0)) + scale_y_continuous (expand = c (0,0)) + geom_abline (intercept = 1, slope = 1, linetype = “dashed”) + theme_bw () 90047 90057 90002 90005 90042 Multiclass settings 90043 90002 We start by building a linear discriminant model using the 90046 iris 90047 data set, which contains the length and width of sepals and petals for three iris species.We want to predict the species based on the sepal and petal parameters using LDA. 90005 90054 90046 # Load the data data ( “iris”) # Split the data into training (80%) and test set (20%) set.seed (123) training.samples% createDataPartition (p = 0.8, list = FALSE) train.data 90047 90057 90002 Performance metrics (sensitivity, specificity, …) of the predictive model can be calculated, separately for each class, comparing each factor level to the remaining levels (i.e. a “one versus all” approach).90005 90054 90046 # Make predictions on the test data predictions% predict (test.data) # Model accuracy confusionMatrix (predictions $ class, test.data $ Species) 90047 90057 90054 90046 ## Confusion Matrix and Statistics ## ## Reference ## Prediction setosa versicolor virginica ## setosa 10 0 0 ## versicolor 0 10 0 ## virginica 0 0 10 ## ## Overall Statistics ## ## Accuracy: 1 ## 95% CI: (0.884, 1) ## No Information Rate: 0.333 ## P-Value [Acc> NIR]: 4.86e-15 ## ## Kappa: 1 ## Mcnemar’s Test P-Value: NA ## ## Statistics by Class: ## ## Class: setosa Class: versicolor Class: virginica ## Sensitivity 1.000 1.000 1.000 ## Specificity 1.000 1.000 1.000 ## Pos Pred Value 1.000 1.000 1.000 ## Neg Pred Value 1.000 1.000 1.000 ## Prevalence 0.333 0.333 0.333 ## Detection Rate 0.333 0.333 0.333 ## Detection Prevalence 0.333 0.333 0.333 ## Balanced Accuracy 1.000 1.000 1.000 90047 90057 90002 Note that, the ROC curves are typically used in binary classification but not for multiclass classification problems.90005 90042 Discussion 90043 90002 This chapter described different metrics for evaluating the performance of classification models. These metrics include: 90005 90012 90013 classification accuracy, 90016 90013 confusion matrix, 90016 90013 Precision, Recall and Specificity, 90016 90013 and ROC curve 90016 90033 90002 To evaluate the performance of regression models, read the Chapter @ref (regression-model-accuracy-metrics). 90005 .90000 Accuracy metrics 90001 90002 90003 Accuracy 90004 class 90005 90006 90003 tf.keras.metrics.Accuracy (name = “accuracy”, dtype = None) 90004 90009 90010 Calculates how often predictions equals labels. 90011 90010 This metric creates two local variables, 90003 total 90004 and 90003 count 90004 that are used to compute the frequency with which 90003 y_pred 90004 matches 90003 y_true 90004. This frequency is ultimately returned as 90003 binary accuracy 90004: an idempotent operation that simply divides 90003 total 90004 by 90003 count 90004.90011 90010 If 90003 sample_weight 90004 is 90003 None 90004, weights default to 1. Use 90003 sample_weight 90004 of 0 to mask values. 90011 90010 90037 Arguments 90038 90011 90040 90041 90037 name 90038: (Optional) string name of the metric instance. 90044 90041 90037 dtype 90038: (Optional) data type of the metric result. 90044 90049 90010 Standalone usage: 90011 90006 90003 >>> m = tf.keras.metrics.Accuracy () >>> m.update_state ([[1], [2], [3], [4]], [[0], [2], [3], [4]]) >>> m.result (). numpy () 0.75 90004 90009 90006 90003 >>> m.reset_states () >>> m.update_state ([[1], [2], [3], [4]], [[0], [2], [3], [4]], … sample_weight = [1, 1, 0, 0]) >>> m.result (). Numpy () 0.5 90004 90009 90010 Usage with 90003 compile () 90004 API: 90011 90006 90003 model.compile (optimizer = ‘sgd’, loss = ‘mse’, metrics = [tf.keras.metrics.Accuracy ()]) 90004 90009 90068 90002 90003 BinaryAccuracy 90004 class 90005 90006 90003 tf.keras.metrics.BinaryAccuracy ( name = “binary_accuracy”, dtype = None, threshold = 0.5 ) 90004 90009 90010 Calculates how often predictions matches binary labels. 90011 90010 This metric creates two local variables, 90003 total 90004 and 90003 count 90004 that are used to compute the frequency with which 90003 y_pred 90004 matches 90003 y_true 90004. This frequency is ultimately returned as 90003 binary accuracy 90004: an idempotent operation that simply divides 90003 total 90004 by 90003 count 90004.90011 90010 If 90003 sample_weight 90004 is 90003 None 90004, weights default to 1. Use 90003 sample_weight 90004 of 0 to mask values. 90011 90010 90037 Arguments 90038 90011 90040 90041 90037 name 90038: (Optional) string name of the metric instance. 90044 90041 90037 dtype 90038: (Optional) data type of the metric result. 90044 90041 90037 threshold 90038: (Optional) Float representing the threshold for deciding whether prediction values are 1 or 0. 90044 90049 90010 Standalone usage: 90011 90006 90003 >>> m = tf.keras.metrics.BinaryAccuracy () >>> m.update_state ([[1], [1], [0], [0]], [[0.98], [1], [0], [0.6]]) >>> m.result (). Numpy () 0.75 90004 90009 90006 90003 >>> m.reset_states () >>> m.update_state ([[1], [1], [0], [0]], [[0.98], [1], [0], [0.6]], … sample_weight = [1, 0, 0, 1]) >>> m.result (). Numpy () 0.5 90004 90009 90010 Usage with 90003 compile () 90004 API: 90011 90006 90003 model.compile (optimizer = ‘sgd’, loss = ‘mse’, metrics = [tf.keras.metrics.BinaryAccuracy ()]) 90004 90009 90068 90002 90003 CategoricalAccuracy 90004 class 90005 90006 90003 tf.keras.metrics.CategoricalAccuracy (name = “categorical_accuracy”, dtype = None) 90004 90009 90010 Calculates how often predictions matches one-hot labels. 90011 90010 You can provide logits of classes as 90003 y_pred 90004, since argmax of logits and probabilities are same. 90011 90010 This metric creates two local variables, 90003 total 90004 and 90003 count 90004 that are used to compute the frequency with which 90003 y_pred 90004 matches 90003 y_true 90004.This frequency is ultimately returned as 90003 categorical accuracy 90004: an idempotent operation that simply divides 90003 total 90004 by 90003 count 90004. 90011 90010 90003 y_pred 90004 and 90003 y_true 90004 should be passed in as vectors of probabilities, rather than as labels. If necessary, use 90003 tf.one_hot 90004 to expand 90003 y_true 90004 as a vector. 90011 90010 If 90003 sample_weight 90004 is 90003 None 90004, weights default to 1. Use 90003 sample_weight 90004 of 0 to mask values.90011 90010 90037 Arguments 90038 90011 90040 90041 90037 name 90038: (Optional) string name of the metric instance. 90044 90041 90037 dtype 90038: (Optional) data type of the metric result. 90044 90049 90010 Standalone usage: 90011 90006 90003 >>> m = tf.keras.metrics.CategoricalAccuracy () >>> m.update_state ([[0, 0, 1], [0, 1, 0]], [[0.1, 0.9, 0.8], … [0.05, 0.95, 0]]) >>> m.result (). Numpy () 0.5 90004 90009 90006 90003 >>> m.reset_states () >>> m.update_state ([[0, 0, 1], [0, 1, 0]], [[0.1, 0.9, 0.8], … [0.05, 0.95, 0]], … sample_weight = [0.7, 0.3]) >>> m.result (). Numpy () 0.3 90004 90009 90010 Usage with 90003 compile () 90004 API: 90011 90006 90003 model.compile ( optimizer = ‘sgd’, loss = ‘mse’, metrics = [tf.keras.metrics.CategoricalAccuracy ()]) 90004 90009 90068 90002 90003 TopKCategoricalAccuracy 90004 class 90005 90006 90003 tf.keras.metrics.TopKCategoricalAccuracy ( k = 5, name = “top_k_categorical_accuracy”, dtype = None ) 90004 90009 90010 Computes how often targets are in the top 90003 K 90004 predictions. 90011 90010 90037 Arguments 90038 90011 90040 90041 90037 k 90038: (Optional) Number of top elements to look at for computing accuracy. Defaults to 5. 90044 90041 90037 name 90038: (Optional) string name of the metric instance. 90044 90041 90037 dtype 90038: (Optional) data type of the metric result. 90044 90049 90010 Standalone usage: 90011 90006 90003 >>> m = tf.keras.metrics.TopKCategoricalAccuracy (k = 1) >>> m.update_state ([[0, 0, 1], [0, 1, 0]], … [[0.1, 0.9, 0.8], [0.05, 0.95, 0]]) >>> m.result (). Numpy () 0.5 90004 90009 90006 90003 >>> m.reset_states () >>> m.update_state ([[0, 0, 1], [0, 1, 0]], … [[0.1, 0.9, 0.8], [0.05, 0.95, 0]], … sample_weight = [0.7, 0.3]) >>> m.result (). Numpy () 0.3 90004 90009 90010 Usage with 90003 compile () 90004 API: 90011 90006 90003 model.compile (optimizer = ‘sgd’, loss = ‘mse’, metrics = [tf.keras.metrics.TopKCategoricalAccuracy ()]) 90004 90009 90068 90002 90003 SparseTopKCategoricalAccuracy 90004 class 90005 90006 90003 tf.keras.metrics.SparseTopKCategoricalAccuracy ( k = 5, name = “sparse_top_k_categorical_accuracy”, dtype = None ) 90004 90009 90010 Computes how often integer targets are in the top 90003 K 90004 predictions. 90011 90010 90037 Arguments 90038 90011 90040 90041 90037 k 90038: (Optional) Number of top elements to look at for computing accuracy.Defaults to 5. 90044 90041 90037 name 90038: (Optional) string name of the metric instance. 90044 90041 90037 dtype 90038: (Optional) data type of the metric result. 90044 90049 90010 Standalone usage: 90011 90006 90003 >>> m = tf.keras.metrics.SparseTopKCategoricalAccuracy (k = 1) >>> m.update_state ([2, 1], [[0.1, 0.9, 0.8], [0.05, 0.95, 0]]) >>> m.result (). Numpy () 0.5 90004 90009 90006 90003 >>> m.reset_states () >>> m.update_state ([2, 1], [[0.1, 0.9, 0.8], [0.05, 0.95, 0]], … sample_weight = [0.7, 0.3]) >>> m.result (). Numpy () 0.3 90004 90009 90010 Usage with 90003 compile () 90004 API: 90011 90006 90003 model.compile ( optimizer = ‘sgd’, loss = ‘mse’, metrics = [tf.keras.metrics.SparseTopKCategoricalAccuracy ()]) 90004 90009 90068 .90000 HTTP / 1.1 404 Not Found 90001 HTTP / 1.1 404 Not Found 90002 The requested resource is not available. 90003 90004 stack trace 90005 90006 com.sapportals.wcm.protocol.webdav.server.WDServletException at com.sapportals.wcm.protocol.webdav.server.WDObject.throwNotFoundIf (WDObject.java:54) at com.sapportals.wcm.protocol.webdav.server.WDGetHandler.handle (WDGetHandler.java:176) at com.sapportals.wcm.protocol.webdav.server.WDServlet.doGet (WDServlet.java: 791) at com.sapportals.wcm.protocol.webdav.server.WDServlet.service (WDServlet.java:483) at javax.servlet.http.HttpServlet.service (HttpServlet.java:853) at com.sapportals.wcm.portal.proxy.PCProxyServlet.service (PCProxyServlet.java:322) at javax.servlet.http.HttpServlet.service (HttpServlet.java:853) at com.sapportals.portal.prt.core.broker.ServletComponentItem $ ServletWrapperComponent.doContent (ServletComponentItem.java:110) at com.sapportals.portal.prt.component.AbstractPortalComponent.serviceDeprecated (AbstractPortalComponent.java: 209) at com.sapportals.portal.prt.component.AbstractPortalComponent.service (AbstractPortalComponent.java:114) at com.sapportals.portal.prt.core.PortalRequestManager.callPortalComponent (PortalRequestManager.java:328) at com.sapportals.portal.prt.core.PortalRequestManager.dispatchRequest (PortalRequestManager.java:136) at com.sapportals.portal.prt.core.PortalRequestManager.dispatchRequest (PortalRequestManager.java:189) at com.sapportals.portal.prt.component.PortalComponentResponse.include (PortalComponentResponse.java: 215) at com.sapportals.portal.prt.pom.PortalNode.service (PortalNode.java:645) at com.sapportals.portal.prt.core.PortalRequestManager.callPortalComponent (PortalRequestManager.java:328) at com.sapportals.portal.prt.core.PortalRequestManager.dispatchRequest (PortalRequestManager.java:136) at com.sapportals.portal.prt.core.PortalRequestManager.dispatchRequest (PortalRequestManager.java:189) at com.sapportals.portal.prt.core.PortalRequestManager.runRequestCycle (PortalRequestManager.java:753) at com.sapportals.portal.prt.connection.ServletConnection.handleRequest (ServletConnection.java:235) at com.sapportals.wcm.portal.connection.KmConnection.handleRequest (KmConnection.java:63) at com.sapportals.portal.prt.dispatcher.Dispatcher $ doService.run (Dispatcher.java:557) at java.security.AccessController.doPrivileged (Native Method) at com.sapportals.portal.prt.dispatcher.Dispatcher.service (Dispatcher.java:430) at javax.servlet.http.HttpServlet.service (HttpServlet.java:853) at com.sap.engine.services.servlets_jsp.server.HttpHandlerImpl.runServlet (HttpHandlerImpl.java:401) at com.sap.engine.services.servlets_jsp.server.HttpHandlerImpl.handleRequest (HttpHandlerImpl.java:266) at com.sap.engine.services.httpserver.server.RequestAnalizer.startServlet (RequestAnalizer.java:386) at com.sap.engine.services.httpserver.server.RequestAnalizer.startServlet (RequestAnalizer.java:364) at com.sap.engine.services.httpserver.server.RequestAnalizer.invokeWebContainer (RequestAnalizer.java:1060) at com.sap.engine.services.httpserver.server.RequestAnalizer.handle (RequestAnalizer.java:265) at com.sap.engine.services.httpserver.server.Client.handle (Client.java:95) at com.sap.engine.services.httpserver.server.Processor.request (Processor.java:175) at com.sap.engine.core.service630.context.cluster.session.ApplicationSessionMessageListener.process (ApplicationSessionMessageListener.java:33) at com.sap.engine.core.cluster.impl6.session.MessageRunner.run (MessageRunner.java:41) at com.sap.engine.core.thread.impl3.ActionObject.run (ActionObject.java:37) at java.security.AccessController.doPrivileged (Native Method) at com.sap.engine.core.thread.impl3.SingleThread.execute (SingleThread.java:104) at com.sap.engine.core.thread.impl3.SingleThread.run (SingleThread.java:176) 90007 .