Классы точности наносят на: Метрология и стандартизация

Метрология и стандартизация

Поможем написать любую работу на аналогичную тему

• Реферат

  Метрология и стандартизация

  От 250 руб

• Контрольная работа

  Метрология и стандартизация

  От 250 руб

• Курсовая работа

  Метрология и стандартизация

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Метроло́гия — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Предметом метрологии является извлечение количественной информации о свойствах объектов с заданной точностью и достоверностью; нормативная база для этого — метрологические стандарты.

Метрология состоит из трёх основных разделов:

• Теоретическая или фундаментальная — рассматривает общие теоретические проблемы (разработка теории и проблем измерений физических величин, их единиц, методов измерений).
• Прикладная — изучает вопросы практического применения разработок теоретической метрологии. В её ведении находятся все вопросы метрологического обеспечения.
• Законодательная — устанавливает обязательные технические и юридические требования по применению единиц физической величины, методов и средств измерений.

Стандартиза́ция — деятельность по разработке, опубликованию и применению стандартов, по установлению норм, правил и характеристик в целях обеспечения безопасности продукции, работ и услуг для окружающей среды, жизни, здоровья и имущества, технической и информационной совместимости, взаимозаменяемости и качества продукции, работ и услуг в соответствии с уровнем развития науки, техники и технологии, единства измерений, экономии всех видов ресурсов, безопасности хозяйственных объектов с учётом риска возникновения природных и техногенных катастроф и других чрезвычайных ситуаций, обороноспособности и мобилизационной готовности страны.

Стандартизация направлена на достижение оптимальной степени упорядочения в определенной области посредством установления положений для всеобщего и многократного применения в отношении реально существующих или потенциальных задач.

За реализацию норм стандартизации отвечают органы стандартизации, наделенные законным правом руководить разработкой и утверждать нормативные документы и другие правила, придавая им статус стандартов.

В области промышленности стандартизация ведет к снижению себестоимости продукции, поскольку:

• позволяет экономить время и средства за счет применения уже разработанных типовых ситуаций и объектов;
• повышает надежность изделия или результатов расчетов, поскольку применяемые технические решения уже неоднократно проверены на практике;
• упрощает ремонт и обслуживание изделий, так как стандартные узлы и детали — взаимозаменяемые (при условии, что сборка осуществлялась без пригоночных операций).

На нашем сайте предоставлены учебные материалы для студентов, по метрологии и стандартизации. Суммарно около

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимостиГарантииОтзывы

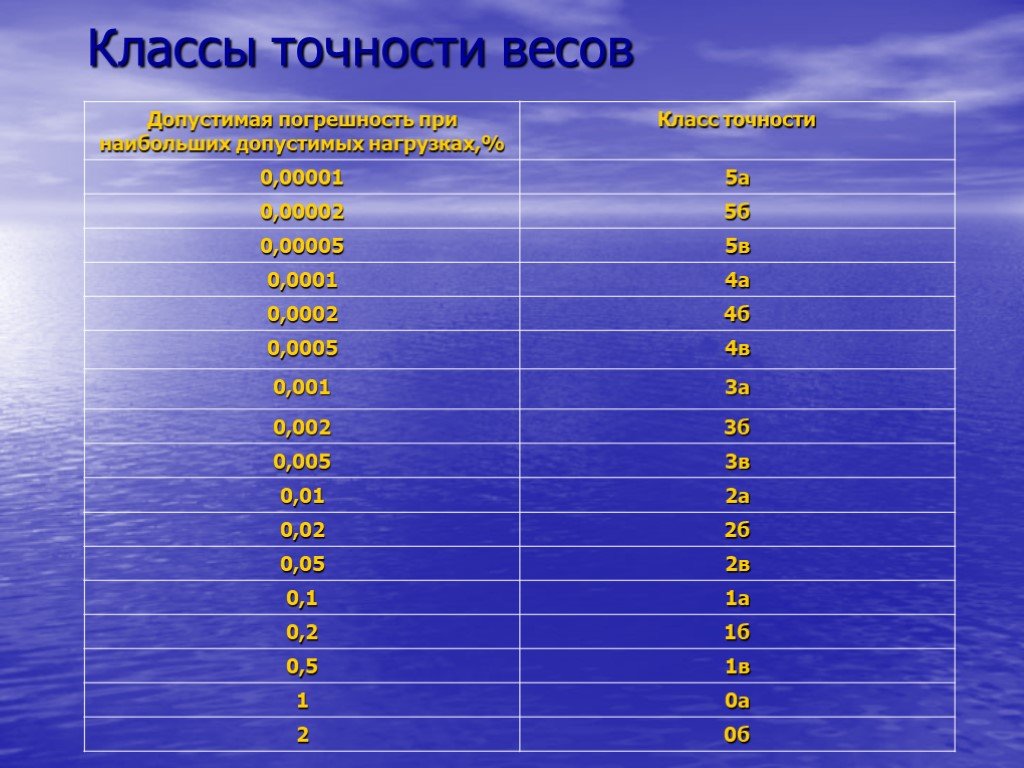
Класс точности средств измерений

В зависимости от основной погрешности средствам измерений присваивают соответствующие классы точности. Класс точности — это обобщенная характеристика средства измерения, определяемая пределами допускаемых основной и дополнительной погрешностей, а также другими свойствами средства измерения, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды средств измерений.

Средства измерений выпускают на следующие классы точ­ности: 0,01; 0,015; 0,02; 0,025; 0,04; 0,05; 0,1; 0,15; 0,2; 0,25; 0,4; 0,5; 0,6; 1,0; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0. Класс точности средств из­мерений

характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств (под точностью средств измерений понимают качество измерений, отражающее близость нулю его погрешностей). На циферблаты, шкалы, щитки, корпуса средств измерений всегда наносят условные обозначения класса точности, включающие числа и прописные буквы латинского ал­фавита.

Пределом допускаемой погрешности средства измерений на­зывается наибольшая (без учета знака) погрешность средства изме­рений, при которой оно может быть признано годным и допущено к применению. Предел допускаемой основной погрешности может выражаться одним из трех способов: в форме абсолютной, отно­сительной и приведенной погрешностей.

Для средств измерений, у которых нормируются абсолютные погрешности, класс точности обозначается

прописными буквами латинского алфавита или римскими цифрами. В определенных случаях добавляется индекс в виде арабской цифры. Такое обо­значение класса точности не связано с пределом допускаемой по­грешности, т.е. носит условный характер.

Для средств измерений, у которых нормируется приведенная или относительная погрешность, класс точности обозначается числами и существует связь между его обозначением и значением предела допускаемой погрешности.

При выражении предела основной допускаемой погрешности в форме приведенной погрешности класс точности обозначается числами, которые равны этому пределу, выраженному в процен­тах. При этом обозначение класса точности зависит от способа выбора нормирующего значения. Если нормирующее значение выражается в единицах

измеряемой величины, то класс точности обозначается числом, совпадающим с приведенной погрешностью. Например, если = 1,5%, то класс точности обозначается 1,5 (без кружка). Если нормирующее значение принято равным длине шкалы или ее части, то обозначение класса точности (при = 1,5%) будет иметь вид 1,5 (в кружке).

При выражении предела допускаемой основной погрешности в форме относительной погрешности необходимо руководство­ваться следующим.

Предел допускаемой основной погрешности согласно выра­жению (2.6)

, (2.10)

где — предел допускаемой абсолютной погрешности; X— из­меренное значение.

В том случае, когда предел относительной погрешности оста­ется постоянным во всем диапазоне измерений, выражение (2.10) принимает вид:

, (2.11)

где с — постоянное число.

Если же предел относительной погрешности изменяется, то

, (2.12)

где с — постоянное число, равное относительной погрешности на верхнем пределе измерения; d — постоянное число, равное по­грешности на нижнем пределе измерения, выраженной в процен­тах от верхнего предела; Хк — конечное значение диапазона изме­рений.

Примеры обозначений класса точности средств измерений представлены в табл. 2.1.

Таблица 2.1.

Стандарты точности

CT — Continental Control Systems, LLC

Трансформаторы тока (ТТ) серии Accu-CT ^® соответствуют требованиям к точности трех широко используемых стандартов:

• ANSI/IEEE C57.13-2008
• МЭК 61869-2:2012
• МЭК 60044-1, издание 1.2 (отменено)

Эти стандарты точности ТТ описывают типичный вторичный выход трансформатора тока как 5 А или 1 А с внешней нагрузкой. Семейства Accu-CT ACTL-0750 и ACTL-1250 имеют встроенные нагрузочные резисторы и обеспечивают выходное напряжение (номинально 0,33333 В переменного тока, также доступно 1,00 В переменного тока). Поправочный коэффициент трансформатора (TCF), точность и пределы фазового угла этих стандартов точности ТТ могут быть применены к выходному напряжению продуктов Accu-CT.

Для получения дополнительной информации см. Стандарты точности счетчиков (AN-136). Каждый из этих классов точности определяет предел для TCF в процентах, поэтому класс 1.2 означает, что TCF TCF должен быть в пределах 1,2 % от идеального при 100 % номинального первичного тока.

Из-за способа определения TCF результирующие пределы усиления (точности) и пределы фазового угла при отображении на графике образуют параллелограмм, что позволяет допускать большие положительные ошибки фазового угла для значений положительного коэффициента коррекции отношения (RCF) и большие ошибки отрицательного фазового угла для отрицательных значений RCF. Логика этого заключается в том, чтобы ограничить наихудшую системную ошибку при использовании ТТ в системе измерения с индуктивной нагрузкой, имеющей коэффициент мощности 0,6.

Для серии Accu-CT мы предлагаем три сорта:

Класс 1.2 (стандартный)

Стандартный класс CT соответствует ограничениям класса точности 1.2 IEEE C57.13, а также более жестким ограничениям по точности и фазовому углу, не требуемым C57. .13.

• TCF: ±1,2 % при 100 % и 120 % номинального первичного тока
• TCF: ±2,4 % при 10 % номинального первичного тока

Расширенные пределы, не требуемые C57.13

• TCF: ±2,4 % при 1 % номинального первичного тока
• Точность: ±0,75 % от 1 % до 120 % номинального первичного тока
• Фазовый угол: ±0,50 градуса (30 минут) от 1% до 120% номинального тока

Класс 0,6

Более высокий класс точности «Опция C0,6» соответствует ограничениям класса точности 0,6 IEEE C57.13, а также более жестким ограничениям точности и фазового угла, не требуемым C57.13.

• TCF: ±0,6 % при 100 % и 120 % номинального первичного тока
• TCF: ±1,2 % при 10 % номинального первичного тока

Расширенные пределы, не требуемые C57.13

• TCF: ±1,2% при 1% номинального первичного тока
• Точность: ±0,50 % от 1 % до 120 % номинального первичного тока
• Фазовый угол: ±0,25 градуса (15 минут) от 1% до 120% номинального тока
• (модели ACTL-0750) ±0,50 градуса (15 минут) ниже 0°C от 1% до 10% номинального тока

Класс 0.

3

Более высокий класс точности «Опция C0.3» соответствует ограничениям класса точности 0.3 IEEE C57.13, а также более жестким ограничениям точности и фазового угла, не требуемым C57.13. Также соответствует или превосходит стандарты IEC 60044-1 и IEC 61869-2, класс 0,5S.

• TCF: ±0,3 % при 100 % и 120 % номинального первичного тока
• TCF: ±1,2 % при 10 % номинального первичного тока

Расширенные пределы, не требуемые C57.13

• TCF: ±1,2 % при 1 % номинального первичного тока
• Точность: ±0,50 % от 1 % до 120 % номинального первичного тока
• Фазовый угол: ±0,25 градуса (15 минут) от 1% до 120% номинального тока
• (модели ACTL-0750) ±0,50 градуса (15 минут) ниже 0°C от 1% до 10% номинального тока

---

Поправочный коэффициент отношения (RCF)

Следующее определение дано в информационных целях, но CCS обычно не использует RCF, вместо этого описывая ту же концепцию, что и точность трансформатора тока. CCS не предоставляет значения RCF для наших ТТ, хотя RCF можно рассчитать на основе «измеренной точности», указанной в сертификате калибровки Accu-CT.

Поправочный коэффициент — это число (обычно близкое к 1,0), которое можно умножить на измеренное значение для получения скорректированного значения. Поправочный коэффициент отношения (RCF) определяется как коэффициент, который при умножении на выход трансформатора тока дает правильный результат:

Например, если предполагается, что ТТ должен быть ТТ 500:0,33333 В переменного тока (500 А на входе дает 0,33333 В на выходе), тогда «отмеченное соотношение» будет 500:0,33333. Если бы фактическое выходное напряжение на входе 500 А составляло 0,340 В переменного тока (высокое значение 2%), то RCF было бы:

Умножение выходного напряжения полной шкалы 0,340 В переменного тока на 0,98038 дает скорректированное выходное напряжение полной шкалы 0,33333 В переменного тока.

Поправочный коэффициент трансформатора (TCF)

Следующее определение дано в информационных целях, но CCS обычно не использует TCF, вместо этого описывая ошибки CT как ошибки точности и фазового угла. CCS предоставляет значения TCF в сертификате калибровки Accu-CT, но WattNode 9В счетчиках 0003 ® не используются поправочные коэффициенты TCF.

Поправочный коэффициент трансформатора (TCF) определяется для трансформаторов тока в стандарте IEEE C57.13 – 2008, стр. 13-14, следующим образом.

• RCF – поправочный коэффициент отношения
• — фазовый угол в минутах (положительный для вторичного сигнала, опережающего первичный ток)

Преобразование этого уравнения в градусы дает:

• фазовый угол в градусах (положительный для вторичного сигнала, предшествующего первичному току)

60044-1 и 61869-2

Пределы точности IEC 60044-1 и IEC 61869-2 проще, чем C57. 13, и определяют только допустимое соотношение (точность) и ошибки фазового угла.

Для Accu-CT мы соответствуем трем классам IEC 60044-1/61869-2. Примечание: некоторые модели Accu-CT доступны в версиях для 50 Гц, оптимизированных для наилучшей работы при 50 Гц, поэтому проверьте техническое описание, чтобы определить, следует ли вам заказывать вариант «50 Гц» для приложений с частотой 50 Гц.

Класс 1.0 (Стандарт)

Стандартный Accu-CT соответствует или превосходит пределы класса точности 1.0.

• Точность: ±1,0 % при 100 % и 120 % номинального первичного тока
• Точность: ±1,5 % при 20 % номинального первичного тока
• Точность: ±3,0% при 5% номинального первичного тока
• Фазовый угол: ±1,0 градуса (60 минут) при 100% и 120% номинального тока
• Фазовый угол: ±1,5 градуса (90 минут) при 20% номинального тока
• Фазовый угол: ±3,0 градуса (180 минут) при 5% номинального тока

Расширенные пределы не требуются согласно 60044-1/61869-2

ТТ стандартного класса также соответствует нашим более строгим ограничениям, которые превышают требования класса 1. 0.

• Точность: ±0,75 % от 1 % до 120 % номинального первичного тока
• Фазовый угол: ±0,50 градуса (30 минут) от 1% до 120% номинального тока

Класс 0,5 и Класс 0,5S

ТТ более высокого класса точности «Опция C0.6» и «Опция C0.3» соответствуют ограничениям класса 0,5 и 0,5S (расширенный диапазон).

• Точность: ±0,50 % при 20, 100 % и 120 % номинального первичного тока
• Точность: ±0,75% при 5% номинального первичного тока
• Точность: ±1,50% при 1% номинального первичного тока
• Фазовый угол: ±0,50 градуса (30 минут) при 20 %, 100 % и 120 % номинального тока
• Фазовый угол: ±0,75 градуса (45 минут) при 5% номинального тока
• Фазовый угол: ±1,50 градуса (90 минут) при 1% номинального тока

Расширенные пределы не требуются согласно 60044-1/61869-2

Трансформаторы тока класса «Опция C0.6» и «Опция C0. 3» соответствуют нашим более строгим ограничениям, которые превышают требования для классов 0,5 и 0,5S.

• Точность: ±0,50 % от 1 % до 120 % номинального первичного тока
• Фазовый угол: ±0,25 градуса (15 минут) от 1% до 120% номинального тока;

  (модели ACTL-0750) ±0,50 градуса (15 минут) ниже 0°C от 1% до 10% номинального тока

Класс 0.2 и класс 0.2S

ТТ более высокого класса точности ACTL-1250 Opt C0.2 соответствуют ограничениям классов 0.2 и 0.2S (расширенный диапазон).

• Точность: ±0,20 % при 20, 100 % и 120 % номинального первичного тока
• Точность: ±0,35% при 5% номинального первичного тока
• Точность: ±0,75 % при 1 % номинального первичного тока
• Фазовый угол: ±0,167 градуса (10 минут) при 20 %, 100 % и 120 % номинального тока
• Фазовый угол: ±0,25 градуса (15 минут) при 5% номинального тока
• Фазовый угол: ±0,50 градуса (30 минут) при 1% номинального тока

Расширенные пределы не требуются согласно 60044-1/61869-2

Трансформаторы тока «Опция C0. 2» соответствуют нашим более строгим ограничениям, которые превышают требования для классов 0,2 и 0,2S.

• Точность: ±0,20 % от 10 % до 120 % номинального первичного тока
• Точность: ±0,30 % от 1 % до 9 % номинального первичного тока
• Фазовый угол: ±0,125 градуса (7,5 минут) от 10% до 120% номинального тока
• Фазовый угол: ±0,250 градуса (15 минут) от 1% до 9% номинального тока

Сбалансированная точность: когда ее следует использовать?

Когда мы обучаем модель машинного обучения, мы хотим знать, как она работает, с помощью нескольких показателей. Пока производительность не станет достаточно хорошей, модель не стоит развертывать, мы должны продолжать итерации, чтобы найти золотую середину, в которой модель не будет ни недообучать, ни переобучать (идеальный баланс).

Существует множество различных показателей для измерения производительности модели машинного обучения. В этой статье мы собираемся изучить основные метрики, а затем немного углубиться в Balanced Accuracy.

Типы проблем в машинном обучении

В машинном обучении есть две общие проблемы: Классификация и Регрессия . Первый имеет дело с дискретными значениями, а второй — с непрерывными значениями.

Классификацию можно разделить на два более мелких типа:

• 1 Двоичный
• 2 Мультикласс

Двоичная классификация

Двоичная классификация имеет две целевые метки, в большинстве случаев один класс соответствует нормальному состоянию, а другой — ненормальному состоянию. Подумайте о модели мошеннических транзакций, которая предсказывает, является ли транзакция мошеннической или нет. Это ненормальное состояние (= мошенническая транзакция) иногда недопредставлено в некоторых данных, поэтому обнаружение может иметь решающее значение, а это означает, что вам могут потребоваться более сложные метрики.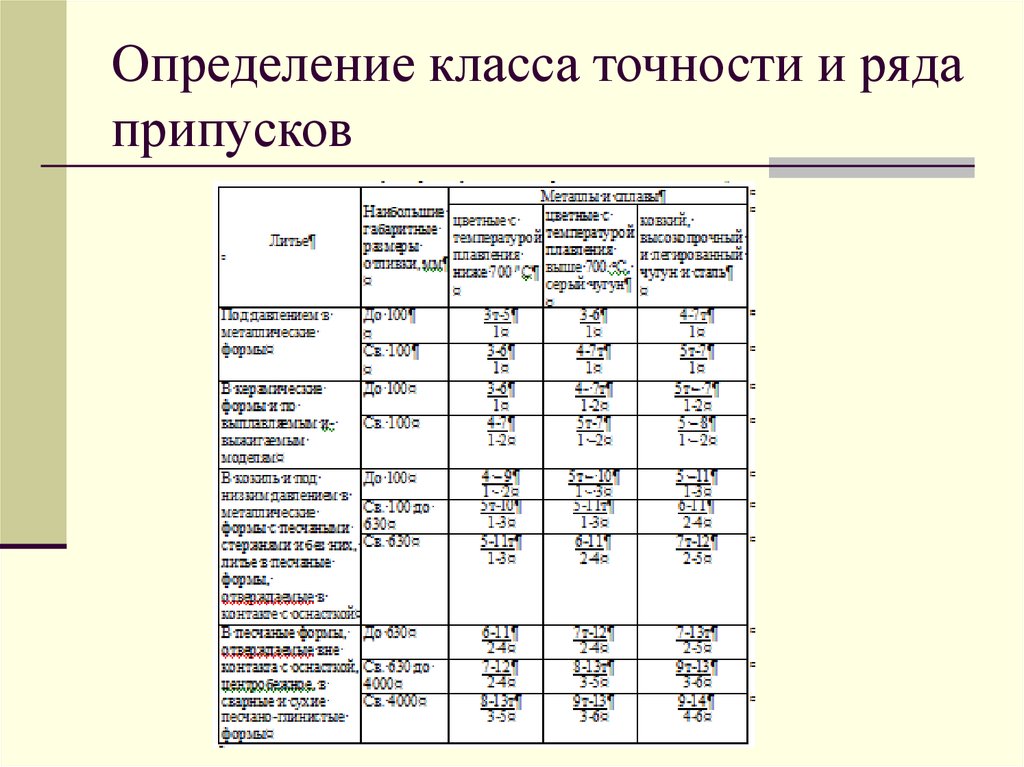

Многоклассовая классификация

В многоклассовой классификации классы равны или больше трех. Задачи мультиклассовой классификации могут быть решены с помощью аналогичного бинарного классификатора с применением некоторой стратегии, т. е. One-vs-Rest или One-vs-One.

См. также

Табличная классификация двоичных данных: все советы и рекомендации по результатам 5 соревнований Kaggle

Бинарная классификация: советы и рекомендации по результатам 10 соревнований Kaggle

Что такое показатель оценки?

Одна из ошибок, которую может совершить начинающий специалист по обработке и анализу данных, заключается в том, что он не оценивает свою модель после ее создания, то есть не знает, насколько эффективна и действенна его модель до ее развертывания. Это может привести к плачевным результатам.

Метрика оценки измеряет производительность модели после обучения. Вы строите модель, получаете обратную связь от метрики и вносите улучшения, пока не получите желаемую точность.

Выбор правильной метрики является ключом к правильной оценке модели машинного обучения. Выбор одной метрики может быть не лучшим вариантом, иногда лучший результат достигается за счет комбинации разных метрик. Различные варианты использования ML имеют разные показатели. Здесь мы сосредоточимся на метриках классификации.

Помните, что метрики — это не то же самое, что функции потерь. Функция потерь показывает показатель производительности модели во время обучения модели. Метрики используются для оценки и измерения производительности модели после обучения.

Одним из важных инструментов, показывающих эффективность нашей модели, является матрица путаницы. Это не метрика, но она так же важна, как и метрика.

Может вас заинтересовать

24 Показатели оценки для бинарной классификации (и когда их использовать)

Матрица путаницы

Матрица путаницы представляет собой таблицу с распределением производительности классификатора по данным. Это матрица N x N, используемая для оценки эффективности модели классификации. Он показывает нам, насколько хорошо работает модель, что нужно улучшить и какую ошибку она допускает.

Где:

• TP – истинно положительный (правильно предсказанный положительный результат класса модели),
• TN – истинно отрицательный (правильно предсказанный результат отрицательного класса модели),
• FP – ложноположительный результат (неверно предсказанный положительный результат класса модели),
• FN – ложноотрицательный (неверно предсказанный результат отрицательного класса модели).

Теперь перейдем к метрикам, начнем с точности.

Точность

Точность — это показатель, который обобщает производительность задачи классификации, это количество правильно предсказанных точек данных из всех точек данных.

Это работает с прогнозируемыми классами, видимыми в матрице путаницы, а не с оценками точки данных.

Точность = (TP + TN) / (TP+FN+FP+TN)

Отзыв

Отзыв — это метрика, которая количественно определяет количество правильных положительных прогнозов, сделанных из всех положительных прогнозов, которые могут быть сделаны модель.

Отзыв = TP / (TP+FN).

Отзыв представляет собой сумму истинно положительных результатов по классам в многоклассовой классификации, деленную на сумму всех истинно положительных и ложноотрицательных результатов в данных.

Отзыв = Сумма(TP) / Сумма(TP+FN)

Отзыв также называется чувствительностью в бинарной классификации.

Macro Recall

Macro Recall измеряет среднее значение отзыва для каждого класса. Он используется для моделей с более чем двумя целевыми классами, это среднее арифметическое отзывов.

Отзыв макроса = (Отзыв1 + Отзыв2 + ——- Отзывn)/n.

Точность

Точность количественно определяет количество правильных положительных прогнозов, сделанных из положительных прогнозов, сделанных моделью. Точность вычисляет точность истинного положительного результата.

Точность = TP/(TP + FP.)

Оценка F1

Оценка F1 поддерживает баланс между точностью и отзывом. Его часто используют, когда распределение классов неравномерно, но его также можно определить как статистическую меру точности отдельного теста.

F1 = 2 * ([точность * отзыв] / [точность + отзыв])

ROC_AUC 

ROC_AUC означает «Характеристика оператора приемника_Область под кривой». Он обобщает компромисс между истинно положительными показателями и ложноположительными показателями для прогностической модели. ROC дает хорошие результаты, когда наблюдения сбалансированы между каждым классом.

Этот показатель невозможно рассчитать на основе сводных данных в матрице путаницы. Это может привести к неточным и вводящим в заблуждение результатам. Это можно увидеть с помощью кривой ROC, эта кривая показывает изменение в каждой возможной точке между истинно положительным уровнем и уровнем ложноположительного результата.

Читайте также

F1 Score против ROC AUC против точности против PR AUC: какую оценочную метрику выбрать?

Balanced Accuracy

Balanced Accuracy используется как в бинарной, так и в многоклассовой классификации. Это среднее арифметическое чувствительности и специфичности, его вариант использования — иметь дело с несбалансированными данными, то есть когда один из целевых классов появляется намного больше, чем другой.

Формула сбалансированной точности

Чувствительность: Это также известно как доля истинно положительных результатов или полнота. Она измеряет долю правильно предсказанных реальных положительных результатов среди всех положительных прогнозов, которые может сделать модель.

Чувствительность = TP / (TP + FN)

Специфичность: Также известная как доля истинно отрицательных результатов, она измеряет долю правильно идентифицированных отрицательных результатов по отношению к общему количеству отрицательных прогнозов, которые может сделать модель.

Специфичность =TN / (TN + FP)

Чтобы использовать эту функцию в модели, вы можете импортировать из scikit-learn:

Двоичная классификация сбалансированной точности

Насколько хороша сбалансированная точность для двоичной классификации? Давайте посмотрим его вариант использования.

При обнаружении аномалий, например при работе с набором данных о мошеннических транзакциях, мы знаем, что большинство транзакций будут законными, т. е. соотношение мошеннических и законных транзакций будет небольшим, сбалансированная точность является хорошим показателем производительности для таких несбалансированных данных.

 Предположим, что у нас есть бинарный классификатор с матрицей путаницы, как показано ниже:

Эта оценка выглядит впечатляюще, но она не обрабатывает столбец «Положительные» должным образом.

Итак, давайте рассмотрим сбалансированную точность, которая будет учитывать дисбаланс в классах. Ниже приведен расчет сбалансированной точности для нашего классификатора:

Сбалансированная точность делает большую работу, потому что мы хотим определить положительные моменты, присутствующие в нашем классификаторе. Это делает оценку ниже, чем предсказывает точность, поскольку дает одинаковый вес обоим классам.

Balanced Accuracy Multiclass Classification

Как и для бинарных, Balanced Accuracy также полезен для мультиклассовой классификации. Здесь BA — это среднее значение отзыва, полученное в каждом классе, т. е. макросреднее значение отзыва для каждого класса. Таким образом, для сбалансированного набора данных оценки, как правило, совпадают с точностью.

Давайте на примере проиллюстрируем, как сбалансированная точность является лучшим показателем производительности в несбалансированных данных. Предположим, у нас есть двоичный классификатор с матрицей путаницы, как показано ниже:

TN, TP, FN и FP, полученные для каждого класса, показаны ниже:

Давайте посчитаем Точность:

Оценка выглядит отлично, но есть проблема. Множества P и S сильно несбалансированы, и модель плохо это предсказывала.

Рассмотрим сбалансированную точность.

Сбалансированная точность = (RecallP + RecallQ + RecallR + RecallS) / 4.

Полнота вычисляется для каждого класса, присутствующего в данных (как в двоичной классификации), при этом берется среднее арифметическое повторений.

При расчете отзыва используется следующая формула:

Отзыв = TP / (TP + FN).

Как вы можете видеть, работа этой модели по прогнозированию истинных положительных результатов для класса P довольно низка.

Как мы видим, этот показатель действительно низок по сравнению с точностью из-за применения одинакового веса ко всем присутствующим классам. Итак, теперь мы знаем, что для получения более высокой оценки необходимо больше данных о классах P, S и R.

Сбалансированная точность и точность классификации

• Точность может быть полезной мерой, если у нас есть аналогичный баланс в наборе данных. Если нет, то может потребоваться Balanced Accuracy. Модель может иметь высокую точность при плохой производительности или низкую точность при лучшей производительности, что может быть связано с парадоксом точности.

Рассмотрим приведенную ниже матрицу путаницы для несбалансированной классификации.

Глядя на точность этой модели, можно сказать, что она высокая, но… она ни к чему не приводит, так как имеет нулевую предсказательную силу (с помощью этой модели можно предсказать только один класс).

Это означает, что модель ничего не предсказывает, а сопоставляет каждое наблюдение со случайно выбранным ответом.

Точность не заставляет нас видеть проблему с моделью.

Здесь хорошо представлены положительные модели.

Итак, в таком случае сбалансированная точность лучше точности.

• Если набор данных хорошо сбалансирован, Точность и Сбалансированная точность сходятся к одному и тому же значению.

Сбалансированная точность по сравнению с F1 Score

Возможно, вам интересно, в чем разница между Balanced Accuracy и F1-Score, поскольку оба они используются для несбалансированной классификации. Итак, давайте рассмотрим это.

• F1 сохраняет баланс между точностью и отзывом

• Оценка F1 не заботится о том, сколько истинно отрицательных результатов классифицируется. При работе с несбалансированным набором данных, который требует внимания к негативам, Balanced Accuracy работает лучше, чем F1.
• В тех случаях, когда положительные результаты так же важны, как и отрицательные, сбалансированная точность является лучшим показателем для этого, чем F1.
• F1 — отличный показатель для несбалансированных данных, когда нужно уделять больше внимания положительным моментам.

Рассмотрим пример:

Во время моделирования данные содержат 1000 отрицательных выборок и 10 положительных выборок. Модель предсказывает 15 положительных образцов (5 истинно положительных и 10 ложноположительных), а остальные — как отрицательные образцы (990 истинно отрицательных и 5 ложноотрицательных).

F1-Score и сбалансированная точность будут:

Вы можете видеть, что сбалансированная точность по-прежнему больше заботится об отрицательных значениях данных, чем F1.

Рассмотрим другой сценарий, где в данных нет истинных отрицательных значений:

Как мы видим, F1 вообще не меняется, в то время как сбалансированная точность показывает быстрое снижение при уменьшении истинного отрицательного значения.

Это показывает, что оценка F1 отдает больший приоритет положительным точкам данных, чем сбалансированной точности.

Balanced Accuracy и ROC_AUC

Чем Balanced Accuracy отличается от ROC_AUC?

Перед тем, как сделать модель, вам нужно учесть такие вещи, как:

• 1 Для чего это?
• 2 Сколько у него возможностей?
• 3 Насколько сбалансированы данные? и т. д.

ROC_AUC похож на Balanced Accuracy, но есть несколько ключевых отличий:

• Balanced Accuracy рассчитывается на предсказанных классах, а ROC_AUC рассчитывается на предсказанных оценках для всех данных, которые не могут быть получены в матрице путаницы. Если проблема сильно несбалансирована, сбалансированная точность является лучшим выбором, чем ROC_AUC, поскольку ROC_AUC проблематичен с несбалансированными данными, т. е. при сильной асимметрии, поскольку небольшое количество правильных/неправильных прогнозов может привести к большому изменению оценки.

• Если нам нужен диапазон возможностей наблюдения (вероятности) в нашей классификации, то лучше использовать ROC_AUC, так как он усредняет все возможные пороги. Однако, если классы несбалансированы и целью классификации является вывод двух возможных меток, то сбалансированная точность является более подходящей.

• Если вас интересуют как положительные, так и отрицательные классы, лучше использовать ROC_AUC.

Реализация сбалансированной точности с двоичной классификацией 

Чтобы лучше понять Balanced Accuracy и другие показатели, я буду использовать эти показатели на примере модели. Коды будут запускаться в блокноте Jupyter. Набор данных можно скачать здесь.

Данные, с которыми мы будем работать, предназначены для обнаружения мошенничества. Мы хотим предсказать, является ли транзакция мошеннической или нет.

Наш процесс будет:

• Загрузка данных,
• Очистка данных,
• Моделирование,
• Предсказание.

Загрузка данных

Как обычно, начинаем с импорта необходимых библиотек и пакетов.

Как видите, данные имеют как числовые, так и категориальные переменные, с которыми будут выполняться некоторые операции.

Посмотрим на распределение классов в целевой, т.е. «мошеннической» колонке.

Давайте посмотрим сюжет.

Мы видим, что распределение разбалансировано, поэтому переходим к следующему этапу — очистке данных.

Очистка данных

Эти данные не имеют значений NAN, поэтому мы можем перейти к извлечению полезной информации из метки времени.

Мы будем извлекать год и час транзакции с помощью кода ниже

Кодирование

Далее следует кодировать строковые (категориальные) переменные в числовой формат. Мы будем маркировать и кодировать его. Sklearn также предоставляет для этого инструмент под названием LabelEncoder.

Поскольку теперь данные закодированы, данные должны выглядеть следующим образом:

Столбцы значений True/False не нужно кодировать, так как это логические значения.

Установка индекса и удаление столбцов

Неважные столбцы в данных должны быть опущены ниже

Масштабирование данных

Нам нужно масштабировать наши данные, чтобы убедиться, что для каждой функции используется одинаковый вес. Для масштабирования этих данных мы будем использовать StandardScaler.

Моделирование

Перед подгонкой нам нужно разделить данные на тестовые и обучающие наборы, это позволяет нам узнать, насколько хорошо модель работает на тестовых данных перед развертыванием. Мы также используем Neptune для регистрации графиков и прогнозов, полученных в результате этого процесса. Это позволит нам легко отслеживать важные метаданные и управлять ими, а также поможет нам быстро получать важную информацию.

После этого разделения мы теперь можем подобрать и оценить нашу модель с помощью показателей оценки, которые мы обсуждали до сих пор, просматривая вычислительный график.

Глядя на графики выше, мы видим, как предсказание модели колеблется в зависимости от эпохи и итерации скорости обучения.

• Хотя точность изначально была высокой, она постепенно падала без идеального спуска по сравнению с другими бомбардирами. Это не очень хорошо отразилось на представлении данных в матрице путаницы.

• Оценка F1 здесь низкая, поскольку она смещена в сторону отрицательных значений в данных. Тем не менее, в приведенных выше данных важны как положительные, так и отрицательные стороны.

• Оценка roc_auc является оценщиком без смещения, обе метки в данных имеют одинаковый приоритет. Эта асимметрия данных не так велика по сравнению с некоторыми данными с соотношением целевой метки 1:100, поэтому ROC_AUC здесь работал лучше.

• В целом, сбалансированная точность хорошо справилась с оценкой данных, поскольку модель не идеальна, над ней все еще можно работать, чтобы получать более точные прогнозы.

Чтобы просмотреть прогноз и сохранить метаданные, используйте код:

Эта функция создает график и регистрирует его в метаданных. Вы можете получить различные кривые, с которыми она работает, из scikitplot.metrics.

Несколько выводов

Мы много обсуждали сбалансированную точность, но вот несколько ситуаций, когда даже самая простая метрика из всех подойдет.

• Когда данные сбалансированы.

• Когда модель не просто отображает результат (0,1), но предоставляет широкий диапазон возможных результатов (вероятность).

• Когда модель должна отдавать предпочтение своим плюсам, чем минусам.

• В многоклассовой классификации, где не придается значения определенным классам.

• Когда существует большая асимметрия или некоторые классы важнее других, сбалансированная точность не является идеальным показателем для модели.

Резюме

Исследование и построение моделей машинного обучения может быть интересным, но также может быть очень разочаровывающим, если не используются правильные показатели. Правильные показатели и инструменты важны, потому что они показывают, правильно ли вы решаете проблему.