Расстояние между станками: Расположение оборудования с точки зрения соблюдения необходимых разрывов и проходов между станками

Расположение оборудования с точки зрения соблюдения необходимых разрывов и проходов между станками

Расположение оборудования с точки зрения соблюдения необходимых разрывов и проходов между станками

Категория:

Проектирования технологических процессов

Расположение оборудования с точки зрения соблюдения необходимых разрывов и проходов между станками

Одним из основных требовании к расположению оборудования будет соблюдение необходимых минимальных габаритных разрывов и проходов между станками, а также между станками и стенами, колоннами и другими предметами оборудования цеха. Это необходимо для обеспечения безопасности работающего, нормальных условий труда и правильной работы станка, а также для свободного прохода и транспортирования полуфабрикатов по цеху.

Ввиду важности этого вопроса законодательством Союза предусмотрены общие нормы и правила расположения оборудования в цехе. Эти правила изложены в книге Якимчика «Законодательство по технике безопасности и промышленной санитарии» и др.

Следует, однако, отметить, что в обязательных постановлениях даны лишь общие указания, как надо располагать станки. Детальное же и точное формулирование всех правил расположения оборудования было бы весьма затруднительно, так как пришлось бы в общих постановлениях охватить чрезвычайное разнообразие способов и случаев расположения оборудования.

Таким образом указанные правила, являясь основанием для разрешения вопроса о расстановке оборудования, — для проектирования цеха, не всегда могут дать достаточное указание, как следует поступать в различных случаях. Ниже приведен ряд таких указаний по расположению станков при проектировании с точки зрения соблюдения необходимых разрывов (полученных из практики):

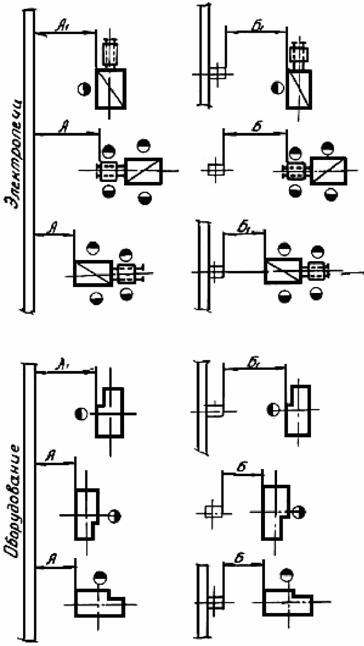
1. Станки должны быть так расположены, чтобы разрывы (расстояния) между ними (а также между станками и частями зданий) были или исключающими возможность прохода между ними , или же, наоборот, не меньше минимального расстояния, обеспечивающего свободный проход.

2. При расположении станков и другого оборудования на плане необходимо для установления надлежащих разрывов показывать на плане (в масштабе) не только станки, но и расположение рабочего во время работы, расположение тележек или ящиков для обрабатываемых деталей (если они размером более 500X500 мм) и транспортеров. Полезно показывать также и расположение вала трансмиссии и шкивов контрприводов. Только при этом условии можно быть уверенным в соблюдении правильных разрывов.

3. Указанные ниже цифры разрывов следует рассматривать как минимально допустимые размеры, меньше которых идти не следует, так как это увеличивает опасность в отношении несчастных случаев, затрудняет работу станков и вызывает ряд неудобств в производстве, а также весьма затрудняет и осложняет междуоперационный транспорт. При увеличении же разрывов надо помнить, что чрезмерное их увеличение влечет за собою излишки в площадях цеха производственных зданий, а стало быть, вызывает излишние капитальные вложения и удорожание производства.

При составлении плана расположения оборудования цеха обычно пользуются масштабом 1 : 50 или 1 : 100, причем станки показываются на плане своими габаритами в соответствующем масштабе. Положение рабочего показывается кружками диаметром 600 мм в принятом масштабе. Валы трансмиссий следует показывать условным пунктиром; также условно обозначаются шкивы трансмиссий и контрприводы. Под габаритом станков принимается контур, очерченный по крайним, выдающимся частям станка, причем для движущихся частей и стола включается в габарит и наибольший размах их как в одну, так и в другую сторону. В габариты автоматов и револьверных станков, предназначенных для прутковой работы, необходимо также включать и величину выступающего у станка прутка. Для протяжных станков в габарит надо включать также протяжный дорн в положении перед началом протяжки. Габариты станков простого очертания обычно представляются в виде очерченного прямоугольника, но в некоторых случаях следует давать и другие формы габаритов, например, для фрезерных, шлифовальных и других станков, в которых форма прямоугольника была бы мало приемлема, так как она не характеризовала бы габарита этих видов станков.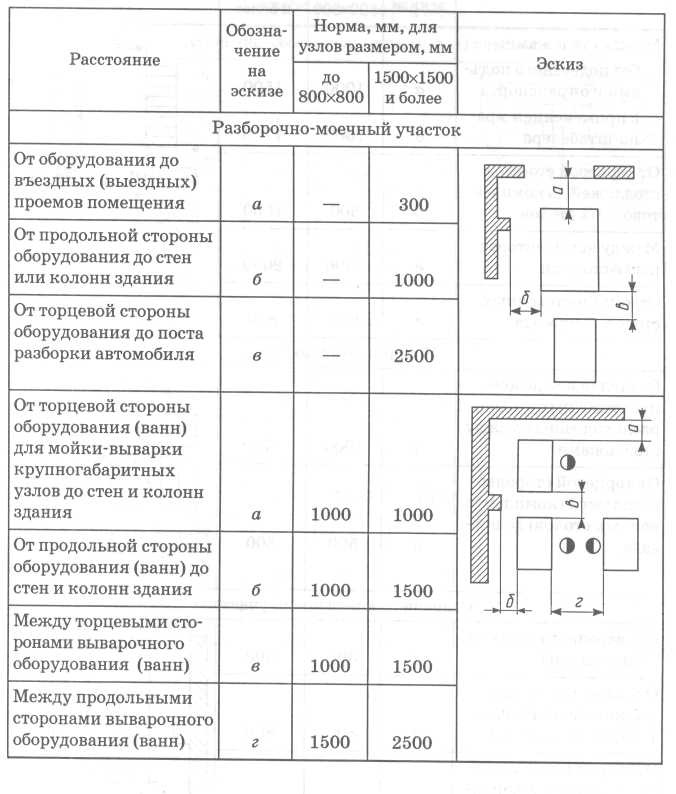

Так, фрезерный станок имеет сравнительно узкое основание и длинный стол, который перемещается в ту или другую сторону на значительную величину. Если очертить станок, в данном случае—в виде прямоугольника, получился бы слишком большой габарит. При пользовании подобными габаритами в планировке площадь цеха не была бы достаточно хорошо использована.

На рис. 1 приведен пример габарита фрезерного станка в виде контура, очерчивающего станок, со всеми выступающими частями и движущимся столом. На этой же фигуре слева показан габарит в его обычном виде, лак это делается при планировке цеха.

Рис. 1. Габарит горизонтально-фрезерного станка,

Рис. 2.

Ниже приведены минимальные размеры разрывов при различных случаях расположений станков.

1. Расстояние от стены или перегородки до задней стороны станка должно, как правило, составлять не меньше 600 мм. При станках мелких размеров и при условии, что сзади станка не имеется движущихся частей и при разрыве между станками по фронту не меньше 600 мм, можно устанавливать станки и вплотную к стене, т.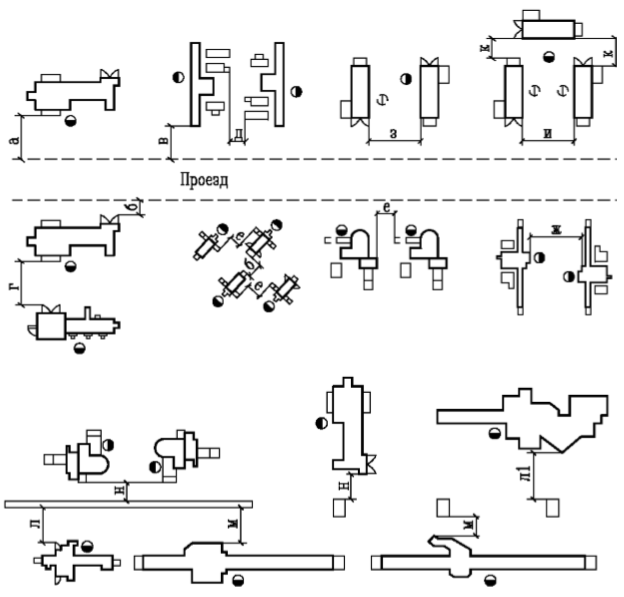 е. на расстоянии около 200 мм от стены.

Расстояние между колонной и задней или боковой стороной станка, на которой нет движущихся частей, должно быть не менее 300 лш. Там, где есть движущиеся части, расстояние должно быть не меньше 400 мм при условии отсутствия необходимости рабочему проходить между станками и колоннами во время работы.

2. Расстояния между станками, Между сторонами станков, где есть движущиеся части, расстояние берется не менее 500— 600 мм.

3. Расстояние между станками меньше 500 мм во избежание прохода рабочего следует заграждать цепочками или перилами. Эти промежутки полезно использовать для установки шкафчиков для инструментов или рабочих столиков. В этом случае заграждения не требуются.

4. Установка верстаков может производиться вплотную к колоннам, стенам или перегородкам. Расстояние между тисками должно быть не меньше 1500 мм при массовом производстве; в случае мелких работ это расстояние может быть снижено до 1000 мм.

5. Общая длина линии станков без проходов, как правило, не должна превышать 25—30 м.

6. При расположении станков так, что между стеной или перегородкой и передней стороной станка или фронтом станка находится рабочий, расстояние между стеной и станком должно составлять не меньше 1000 мм.

При наличии у стены отопительных и других устройств на высоте не свыше 2 м от уровня пола указанное расстояние надо считать от наиболее выступающих частей на стене.

7. Расстояние между задней и передней стороной станков при наличии одного рабочего между ними и при отсутствии общего прохода, движения тележки и т. д., — должно составлять не меньше 1000 мм.

Рис. 3.

Рис. 4.

8. Расстояние между фронтами станков, т. е. при наличии двух рабочих между ними, но без движения тележек и общего прохода, должно быть не менее 1502 мм. При крупных станках это расстояние увеличивается до 2000 мм. При обслуживании же одним рабочим двух станков расстояние между фронтами этих станков принимается около 1000 мм, если между этими станками нет общего прохода.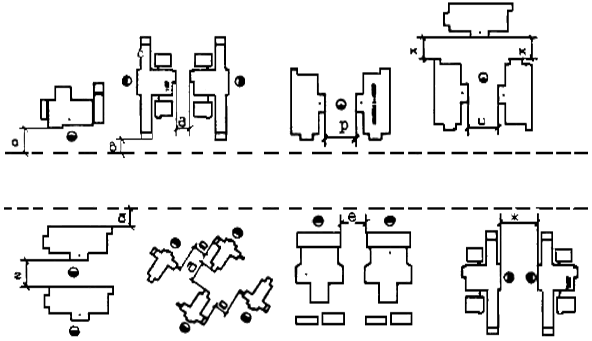

Рис. 5.

9. Минимальный размер проходов для движения тележек определяется следующим образом:
а) при движении тележек в одном направлении величина проходов между рядами станков, обращенными фронтами к проходу, т. е. при наличии двух рабочих в проходе, составляется из ширины габарита нагруженной тележки, плюс по 700 мм на каждое рабочее место, — т. е. 2000 мм и выше;
б) при наличии одного рабочего места величина прохода равна 700 мм на рабочее место плюс 400 мм на промежуток от задней стороны другого станка до габарита тележки и плюс ширина габарита нагруженной тележки, т. е. 1700 мм и выше;
в) расстояние между рядами станков, обращенных к проходу задними или боковыми стенками, берется равным ширине габарита нагруженной тележки плюс 400 мм с каждой стороны тележки, от линии станков до габарита тележки, т. е. 1500 мм и выше;
г) при встречном движении тележек (в ту и другую стороны) сохраняются те же составные данные для общей ширины прохода и, кроме того, прибавляется общая ширина габарита второй тележки и 300 мм на зазор между тележками для их разъезда;

д) для прохода, без движения тележек, следует прибавить к рабочему месту еще 700 мм (для свободного прохода). Таким образом в этом случае, при одном рабочем в проходе, ширина его будет не меньше 1400 мм и при двух рабочих в проходе — не меньше 2100 мм;
е) при наличии в проходах вместо тележек других видов транспорта, например, рольгангов, гладких столов, конвейеров и пр., величина проходов определяется описанным выше способом, т. е. к величине габарита, занимаемого транспортными устройствами, добавляются указанные выше размеры. Проходы между стеной, перегородкой или колонной и линиями станков определяются также изложенным выше способом.

Рис. 6.

Рис. 7.

Рис. 8.

10. Крупные и сложные станки располагаются обычно более свободно, так как это бывает необходимо для их наладки и, в особенности, для всякого рода ремонта на месте. В этих случаях следует давать разрывы кругом станка не менее 500—600 мм. Если же станок требует и обслуживания с различных сторон во время работы, то следует разрывы для таких станков давать не менее 1000 мм.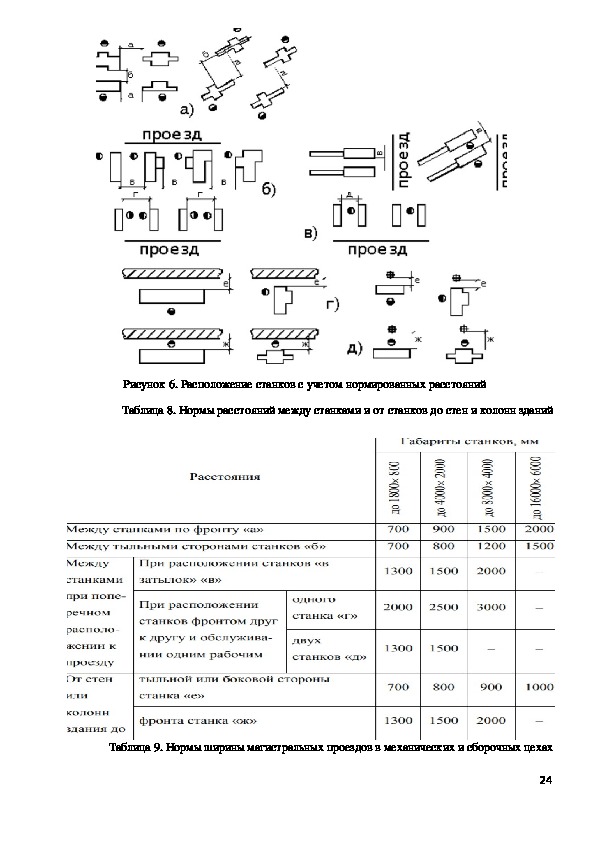

11. Станки, обрабатывающие крупные детали, в особенности в серийном производстве, должны располагаться также более свободно, учитывая необходимые площади для необработанных и обработанных деталей в пределах намеченных размеров партий или серий этих деталей.

12. Станки, обслуживаемые одним рабочим, расположенные в линию, необходимо ставить возможно ближе друг к другу, вплоть до самых минимальных разрывов, для облегчения их обслуживания. Это ведет к уменьшению вспомогательного времени обработки и увеличению производительности.

13. В массовом производстве, в целях наиболее надежной поточности и наилучшей увязки рабочего места с транспортированием деталей следует, как правило, в направлении потока давать также минимальные разрывы, поскольку увеличение разрывов не требуется какими-либо особыми производственными условиями или особенностями станка.

14. Для большинства станков следует признать более целесообразным, с точки зрения использования площади цеха, ставить станки задними сторонами друг к другу. Это позволяет свести к минимуму промежутки между ними и увеличить проходы.

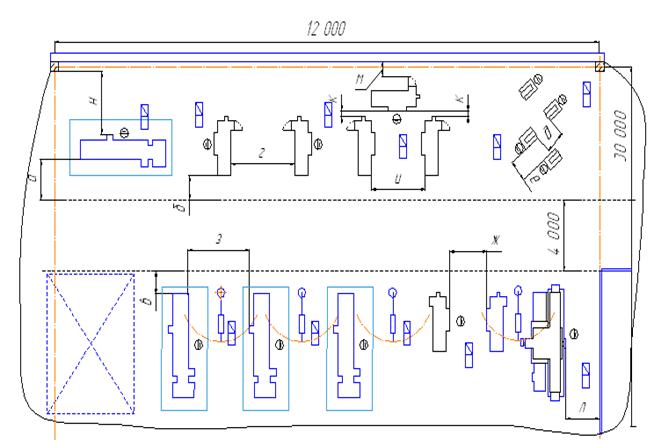
Приведем несколько примеров расположения оборудования с точки зрения соблюдения необходимых разрывов. На рис. 286 показан пример продольного расположения токарных станков в многоэтажном здании для серийного производства.

Помимо станков, на упомянутых фигурах показано расположение и рабочих во время работы, а также расположение инструментальных шкафчиков и габариты проходов, в зависимости от габарита тележки.

Рис. 9.

Продольное расположение для многоэтажных зданий является обычным, в особенности при трансмиссионном или групповом приводе станков, так как в этом случае трансмиссионное валы удобнее располагать вдоль здания. При индивидуальных моторах можно применять то или иное расположение, но надо отметить, что и в этих случаях для многоэтажных зданий продольное расположение является, обычно, более удобным.

Рис. 10

В одноэтажных зданиях, с верхним светом, продольное и поперечное расположение станков обычно не различается, так как здесь безразлично вдоль какой оси здания располагать станки.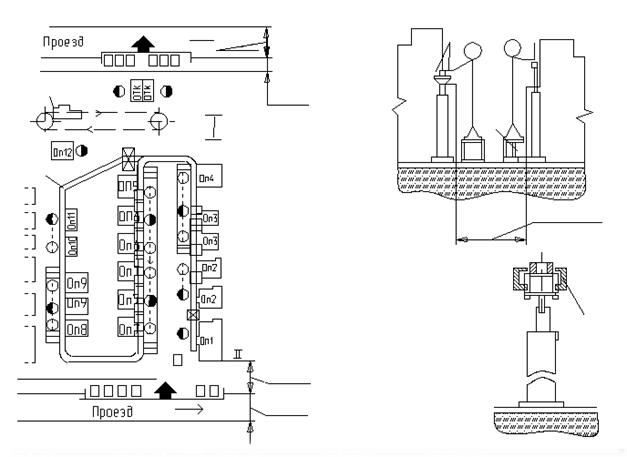 Предпочтительнее, однако (с точки зрения использования площади цеха) при различной ширине пролета располагать станки вдоль более широких пролетов.

Более сложным представляется вопрос расположения прутковых автоматов, а также и прутковых револьверных станков. Расположение этих станков в значительной мере зависит от конструкции, размеров станка, длины обрабатываемых прутков, количества установленных в цеху автоматов, а также и количества станков, обслуживаемых одним рабочим. Помимо этого, при расположении станков приходится особенно считаться с конфигурацией здания и отводимой площадью под эти станки. Расположение прутковых автоматов и револьверных станков затрудняется в особенности из-за необходимости оставления достаточного места для зарядки этих станков, которая производится с фронта или с тыла станка: пруток обычно помещается или в целую газовую трубу, поддерживаемую специальными подставками, или вставляется в две небольших трубы, из которых одна находится у станка, а другая на стойке, в конце прутка. Иногда пруток помещается в раскрывающийся на две половины желоб, деревянный или из листового железа. Это позволяет легко вкладывать пруток непосредственно с фронта станка.

По большей части автоматы располагаются таким образом, что зарядка производится с тыла станка, причем прутки вращаются в газовых трубах. Объясняется это тем, что не всякая конструкция автомата допускает удобно зарядку с фронта. В особенности это относится к автоматам больших размеров. При зарядке с фронта труба ставится несколько наискось от оси автомата и пруток заводится в трубу спереди. При такой зарядке требуется меньше дополнительной площади для выдвинутого из трубы прутка, чем это необходимо для зарядки с тыла. При зарядке автомата с тыла необходимо к занимаемой во время работы длине прутка прибавить размер выдвинутого прутка из поддерживающей трубы с таким расчетом, чтобы не загораживать прохода (или же давать специальный проход для зарядки автоматов).

Существует два основных способа расположения автоматов: 1) наклонное расположение и 2) попарное расположение.

Попарное расположение автоматов, несмотря на ряд преимуществ перед наклонным, значительно реже встречается в практике и, главным образом, из-за того, что обслуживание в этом случае группы станков одним рабочим более затруднительно, чем при наклонном расположении. Оба эти способа обладают своими достоинствами и недостатками. Следует отметить, что наклонное расположение автоматов является несколько более компактным, чем попарное расположение, хотя разница между тем и другим способом по занимаемой площади в общем довольно незначительна.

Рис. 11.

Фирмы, изготовляющие мелкие автоматы, иногда рекомендуют производить расположение своих автоматов в порядке попарного расположения, основываясь на нижеследующих доводах: такое расположение не дает никакого изменения в направлении поперечных проходов и дает некоторое удобство при зарядке станков. При наклонном же расположении и при наличии большой группы автоматов рабочему для зарядки приходится проходить всю линию станков, если станки заряжаются с тыла.

Далее, при наклонном расположении контрпривод должен быть поставлен точно над шкивом станка, тогда как для попарного расположения это не имеет существенного значения. При попарном расположении труба, в которой находится пруток, может быть свободно выдвинута влево от рабочего места, благодаря чему получается более удобная зарядка с фронта, чем при наклонном расположении станков. Зарядка с фронта при наклонном расположении для некоторых автоматов, в силу особенности их конструкции (если главный шкив расположен со стороны прутка), иногда бывает весьма неудобна или даже совеем невозможна. К преимуществам наклонного расположения следует отнести то обстоятельство, что станки расположены фронтами в одну сторону и на небольшом расстоянии друг от друга благодаря чему значительно облегчаются условия наблюдения и обслуживания всей линии станков. Иногда при обоих способах расположения автоматы расставляются таким образом, что проходы получаются по диагоналям, как показано на рис. 294—295.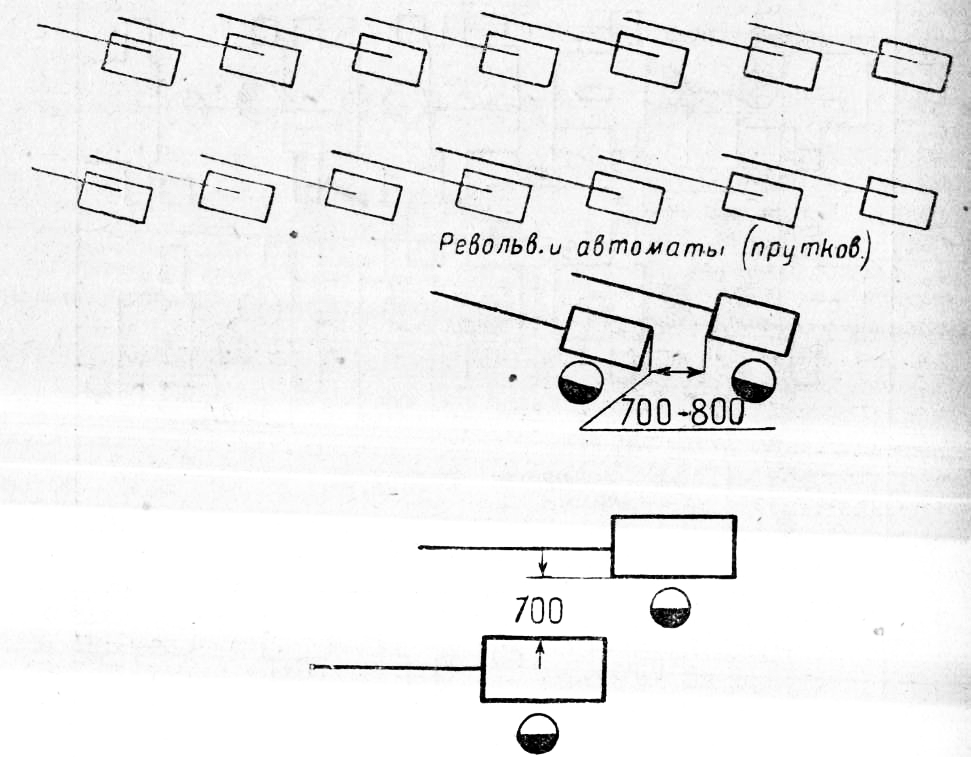 Такое расположение автоматов обычно занимает несколько большее место, но зато представляет больше удобства в смысле их обслуживания и зарядки.

Рис. 12.

При расположении станков необходимо учитывать, какая длина обрабатываемого прутка будет поступать в цех. Обычно на рынке имеются прутки длиною 5—6 м, но не всегда на автоматы пускают прутки этой длины. Обычно их разрезают на две половины, благодаря чему проходы между станками сильно уменьшаются и облегчается зарядка станков, в особенности для прутков больших диаметров. При прутках особенно больших размеров (свыше 60 мм) обычно заправка автоматов ведется прутками еще меньшей длины. Расстояние между прутками и соседними станками получается часто весьма незначительное: пруток почти вплотную подходит к корыту или к щиту автомата. Но в работе этот пруток совсем не мешает, так как рабочему весьма редко приходится заходить на противоположную сторону станка, собирание уже обработанных деталей или удаление стружки производится с передней стороны станка.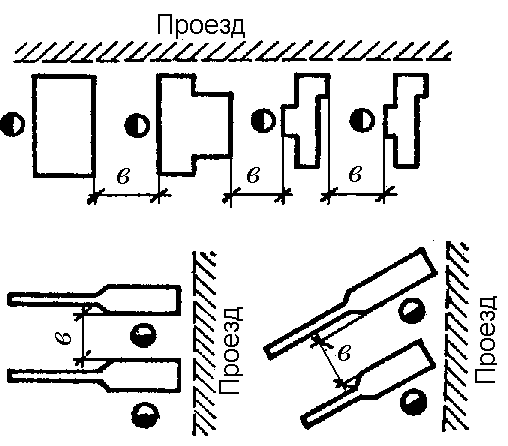 Однако при четырехшпиндельных и шестишпиндельных автоматах это расстояние следует увеличивать до 300 — 400 мм. Автоматы, обслуживаемые с обеих сторон должны иметь расстояние от задней стороны до прутка соседнего автомата не менее 700 мм.

При наклонном расположении автоматы ставятся обычно под углом от 10 до 20° и редко больше. Выбор этого угла зависит от конструкции станка, длины прутков и местных условий расположения станков в цеху. При наклонном расположении автоматов следует их ставить небольшими группами при зарядке станков с тыла, так, чтобы рабочему приходилось проходить не больше 10—16 м для зарядки.

На рис. 13 дан пример наклонного расположения автоматов в многоэтажном здании для зарядки с фронта и с. тыла. Расстояние между автоматами при наклонном расположении зависит от того, откуда производится его зарядка. При зарядке с фронта следует давать разрыв между ними от 600 до 700 мм в зависимости от размеров станка и прутка. При зарадяке с тыла можно уменьшить этот размер до 400—600 мм. При больших размерах автоматов и прутков, следует эти размеры увеличивать, причем не рекомендуется применять способы зарядки с фронта. В особенности это относится к многошпиндельным автоматам.

В отношении револьверных станков нужно сказать то же самое, хотя при небольших размерах и простых конструкциях револьверных станков можно несколько и уменьшить указанные выше размеры.

Рис. 13.

Рис. 14.

Для этих станков чаще применяют способы наклонного расиоложения и зарядки с фронта, так как это дает лучшее использование площади.

На рис. 15 показано наклонное расположение автоматов с оставлением между ними проходов (продольных). В таких случаях расстояния между автоматами (между параллельными их сторонами) делаются от 600 до 800 мм в зависимости от размеров автоматов. Такой способ является обычным для многошпиндельных, а также крупных автоматов.

Рис. 15.

Реклама:

Читать далее:

Расположение оборудования с точки зрения соблюдения правильных производственных потоков

Статьи по теме:

Нормы расстояний между станками – Энциклопедия по машиностроению XXL

Нормы расстояний между станками и от станков до стен и колонн здания, а также нормы ширины проездов и расстояний между рядами станков приведены в табл. 13 и 14. Эти нормы входят в состав норм технологического проектирования, пересмотренных в соответствии с Постановлением Совета Министров СССР от 28 июля 1972 г. № 560 О мерах по обеспечению снижения сметной стоимости строительства и утвержденных по согласованию с Госстроем СССР в 1973 г.  [c.23]
Нормы расстояний между станками и от станков до стен и колонн здания  [c.24]

Нормы расстояний между станками п их складочными местами для разных схем организации рабочего места [7]  [c.108]

II. Нормы расстояний между станками и элементами зданий [7]  [c.109]

Нормы расстояний между станками по фронту и между тыльными  [c.343]

Нормы расстояний между станками при поперечном расположении их по отношению к проезду  [c.346]

Нормами расстояний между станками не учитываются площадки для хранения деталей.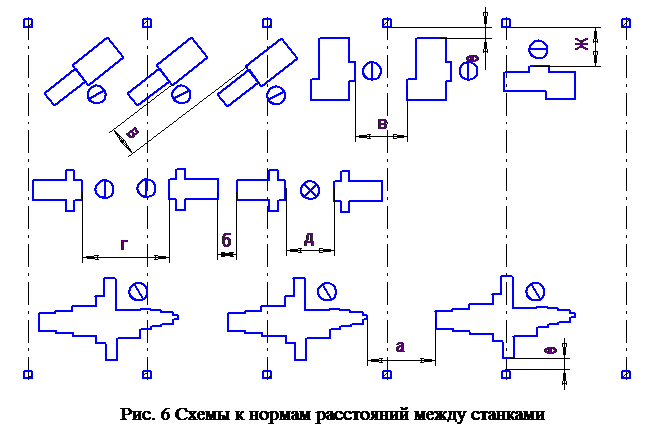 у станков, а также устройства для транспортировки деталей между станками, которые принимаются дополнительно в зависимости от условий планировки и характера производства.  [c.837]

Нормы расстояний между станкам  [c.1212]

Нормы расстояний между станками и строительными конструкциями зданий  [c.1215]

При планировке оборудования цеха следует предусматривать в продольном направлении, а при длине производственной части корпуса свыше 100 м н в поперечном направлении магистральные (главные) проезды. Нормы на внутрицеховые проезды, проходы, на расстояния между станками и рабочими местами принимаются по существующим нормам для механических цехов.  [c.327]

Проектируемые цехи (отделения) должны иметь достаточную площадь, соответствующие нормам безопасности расстояния между станками и размеры проездов и проходов, правильную организацию рабочих мест, оборудование, оснащенное эс ективными оградительными устройствами, соответствующий уровень механизации перемещения материалов и готовой продукции.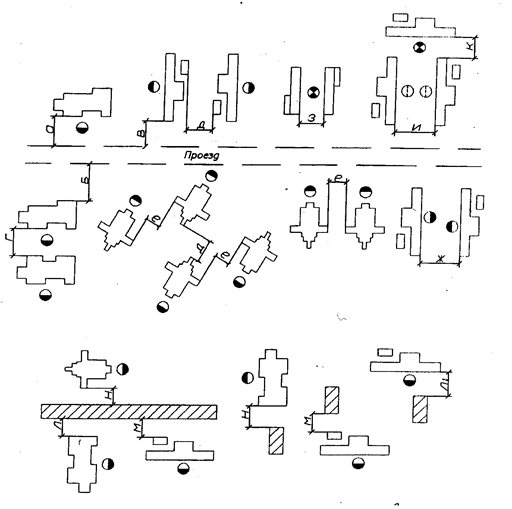  [c.114]

Рис, 76. Схемы к нормам расстояний между рядами станков 178  [c.178]

Нормы расстояний между прутковыми токарными автоматами, револьверными станками и станками, расположенными под углом  [c.347]

Буквами обозначены расстояния между станками и элементами здания цеха, ширина цеховых проходов и проездов. Ниже приведены нормы (в мм) для среднегабаритных станков (от 1500 X 750 до 3500 X 2000 или весом до 5 тс) 600 — расстояние между станками по фронту 700 — расстояние между тыльными сторонами станков 500 — расстояние от стены (выступающих конструкций) до тыльной стороны станка, а также расстояние от стены (выступающих конструкций) до боковой стороны станка 1500 — расстояние от стены (выступающих конструкций) – до фронта станка 500 — расстояние от колонны до тыльной и боковой сторон станка 900 — расстояние от колонны до фронта станка 1100 — расстояние между одношпиндельными токарными автоматами или револьверными станками при поперечном расположении по отношению к проезду 1700 — ширина цеховых проходов и проездов для ручных тележек, шириной до 700 мм между одним рядом станков, расположенных тыльной стороной, и вторым рядом станков, расположенных по фронту,  [c.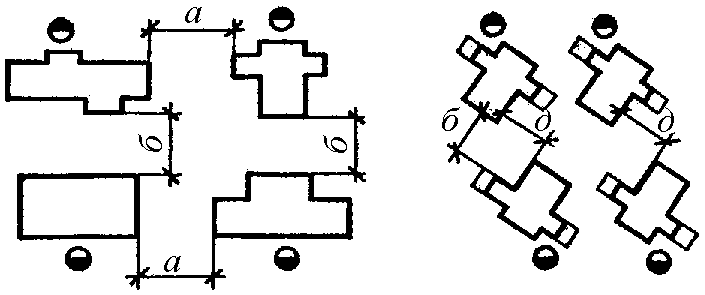 465]

В Нормах приводятся необходимые данные для определения общего количества основных станков РМЦ и ЦРБ при различной серийности производства коэффициенты загрузки оборудования РМЦ и ЦРБ примерное распределение станков по типам в РМЦ и ЦРБ состав вспомогательного оборудования для РМЦ и ЦРБ нормы годового расхода материалов на один основной станок РМЦ примерное распределение материалов по видам размеры проездов в цехе, расстояния между станками и от станков до стен здания площадь на одну единицу основного оборудования РМЦ и ЦРБ нормы площадей вспомогательных помещений количество работающих в РМЦ и ЦРБ в зависимости от числа основного оборудования этих подразделений. Все эти данные обеспечивают возможность разработки проекта РМЦ и ЦРБ предприятия.  [c.108]

Нормы ширины проездов и расстояний между рядами станков  [c.25]

Нормы ширины цеховых проездов и расстояний между линиями станков и складочными местами [7]  [c. 114]

Нормы точности направляющих станин для всех станков определяются ГОСТ. По ГОСТ направляющие должны быть параллельны. Допускаемые отклонения на длине 1000 мм составляют 0,02 мм при расстоянии между направляющими до 1. и и 0,03 мм при расстоянии между ними до 2 м. Направляющие станины должны быть прямолинейны в горизонтальной плоскости. Допускаемые отклонения составляют 0,02 мм на 1000 мм длины и от 0,03 до  [c.225]

Возникновение погрешностей трех видов — это единый и непрерывный процесс, который может быть представлен как образование во время обработки неправильной криволинейной поверхности вследствие изменения в каждой точке обрабатываемой поверхности расстояния между кромкой режущего инструмента и базами станка, причем изменения расстояний могут быть вызваны как относительным перемещением режущего инструмента и баз станка в направлении нормали к обрабатываемой поверхности, так и их поворотом в пространстве. На рис. 9.1 схематично и только в одной из вертикальных плоскостей отображено образование погрешностей формы, относительного поворота и расстояния обрабатываемой поверхности детали при торцовом фрезеровании как следствие непрерывного изменения расстояния 2 и угла поворота 8 фрезы относительно стола станка.  [c.634]

Осмотром установить нет ли выбоин НЛП неровностей, пролитого масла или охлаждающей жидкости, стружки или посторонних предметов на площади рабочего места фрезеровщика соответствуют ли расстояния между тумбочками, стеллажам , шкафами и станками действующим нормам, не загромождены ли они приспособлениями или посторонними предметами, на месте ли подножная решетка, не нарушено ли заземление (рис. 1). Указанные недостатки могут быть причиной травматизма или несчастного случая. Поэтому при обнаружении их немедленно сообщить об этом мастеру, затем устранить недостатки и навести порядок на рабочем месте.  [c.6]

Проверка пятна контакта и направления зубьев. Точность выполнения боковой поверхности зубьев конических колес обычно проверяется на универсальных и специальных контрольно-обкатных станках (см. табл. 9.2). Станки имеют две бабки, оси которых устанавливаются в соответствии с углом между осями передачи. Кроме того, бабки смещаются вдоль осей для обеспечения базовых расстояний торцов колес от точки пересечения осей. Шпиндель одной из бабок вращается при помощи электродвигателя, а вращение шпинделя второй бабки ограничивается тормозом. После кратковременного вращения зубчатой пары на зубьях проверяют размеры и расположение следов пятна контакта. Для достижения требующегося пятна контакта применяют регулировку положения бабок и по результатам ведут подналадку зубообрабатывающего станка [6]. Нормы точности контрольно-обкатных станков даны в ГОСТ 16473—80.  [c.256]

Гипроавтопролюм установлены нормы, определяющие расстояния между станками и расстояния от станков до элементов здания в зависимости от размеров станков (табл. 18—23).  [c.350]

При выработке планировочного решения следует учитывать, что для лучшей организации производствен-Н010 процесса на участке его целесообразно делить на две зоны, в одной из которых размещается оборудование для слесарных работ, в другой — для механических. Металлорежущие станки в своей зоне обычно размещают по типам группами револьверные, токарно-винторезные, фрезерные, строгальные, шлифовальные. Расстояния между станками определяются нормами, оговоренными ранее и обеспечивающими безопасность и удобство работы. Проходы между станками должны быть прямолинейными. При размещении оборудования необходимо учитывать возможность использования подъемно-транспортных средств. Револьверные станки следует размещать загрузочной стороной под углом 15…30° к проходу, чем облегчается их загрузка и улучшается использование производственной площади. Сверлильные станки следует располагать ближе к слесарным рабочим местам.  [c.299]

Измерение колебания длины общей нормали. Длиной общей нормали называется расстояние между двумя параллельными охватывающими губками, касательными к двум разноименным профилям зубьев. При этом между губками располагается примерно z/9 зубьев. Колебание длины общей нормали в пределах одного колеса характеризует составляющую кинематической погрешности колеса, зависящую от неточностей цепи обката зубообрабатывающего станка. Второй составляющей кинематической потрешности колеса является радиальное биение зубчатого венца. Колебание длины общей нормали не зависит от радиального биения зубчатого венца колеса [23] и измеряется с помшцью нормалемеров, имеющих неподвижную координирующую плоскую и параллельную ей подвижную измерительные губки. Различие в длине общ й нормали в различных участках колеса воздействует на стрелку отсчетного устройства рис. 9.11) или же отсчитывается по шкале в микрометрических нормалемерах (рис. 9.12). Методы и средства поверки нормалемеров изложены в ГОСТ 8.169—75.  [c.247]

При двухпрофильном контроле выявляются радиальное биение зубчатого венца, биение зубообразующего инструмента, а также погрешности шага зацепления и профиля зубьев колеса. Тангенциальные погрешности обработки, такие, как кинематическая погрешность делительной передачи станка, совершенно не выявляются при двухпрофильном комплексном контроле, так как эти погрешности не создают изменения радиального расстояния между изделием и инструментом в процессе зубообработки и поэтому не вызывают изменения межосевого расстояния при двухпрофильном контроле.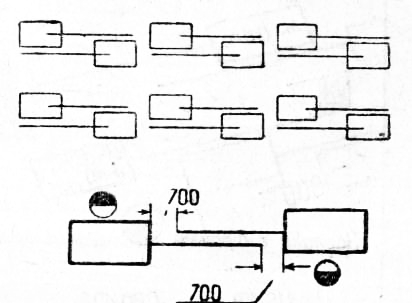 Учитывая это обстоятельство, в комплексах контроля Зя4 (табл. П.12), кроме двухпрофильного контроля, предусмотрен контроль тангенциальной составляющей общей кинематической погрешности колеса либо по колебанию длины общей нормали или же по погрешности обката.  [c.452]

Недопустимая величина бокового зазора в червячной паре суппорта станка приводится к норме путем регулирования расстояния между осями червяка и червячного колеса. Конструкцией предусмотрена возможность этого регулирования путем перешли-4ювки промежуточной пластины между корпусами суппорта и червяка.  [c.233]

После вычерчивания на плане каждой единицы оборудования (станка, стенда и т. п.) ее расположенпе в проектируемом пролете обозначается размерами расстояний (в продольном и поперечном направлениях) от ближайшей колонны. Разрывы между станками и рабочими местами (стендами), между ними и ближайшими частями здания (колоннами и стенами), а также ширина рабочих проходов и проездов устанавливаются в соответствии с нормами технологического проектирования (см. табл. 35 и 36), а также условиями, обеспечивающими удобства для выполнения работ. Наименьшие допускаемые значения этих величин для различных случаев относительного расположения рабочих мест, оборудования ]1 рабочих показаны на следующих примерах типовых планировок.  [c.251]

Нормы точности изготовления водила, связанные с точностью нарезания зубчатых колес, отсутствуют. Если отверстия в водиле растачиваются с помощью делительного приспособления, то с увеличением диаметра погрешность возрастает. При обработке водила на координатно-расточном станке погрешность определяется лишь классом -станка. Обычно для передач с зубчатыми колесами степени точности 7—о по ГОСТ 1643—72 ошибка межосевого расстояния и расстояния между соседними сателлитами составляет Д = 70 -120 мкм при диаметре начальной окружности центрального колеса — 250ч-1000 мм. Для передач с зубчатыми колесами 5-, 6-й степени точности Д = 50-г-100 мкм при (d )h = 250-ь 1500 мм. Указанные значения допусков принимаются также при расчете смещений e ,a и е ь.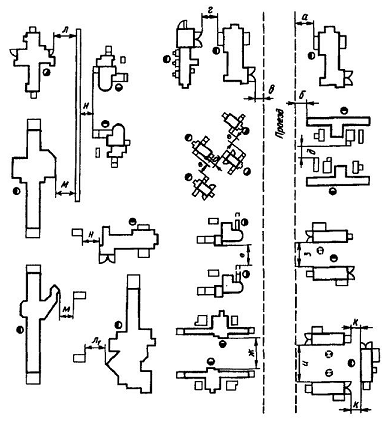  [c.245]

П. может быть конической или цилиндрической. Особенно эффективно производство цилиндрических П. больших размеров. В этих передачах у зубьев одного из колес плоские боковые поверхности, у второго колеса (значительно меньшего по размерам) зубья со специальным сопряженным профилем. Нарезаются такие зубья на специальных станках (станках Г. А. Анопова) дисковыми фрезами, расположенными, как показано на сх. а, на расстоянии , равном длине общей нормали. Фрезы образуют прорези при циклическом последовательном повороте колеса-заготовки. Часть металла, заключенная между прорезями, выпадает и пoлyчaet-  [c.316]

---

Рис. 3.1. Варианты расположения оборудования и маршруты движения рабочего при многостаночном обслуживании

Рисунок Рис. 3.1. Варианты расположения

(не приводится) оборудования и маршруты движения

рабочего при многостаночном

обслуживании

При циклическом обслуживании станков, расположенных линейно (I вариант планировки), рабочий-многостаночник по окончании цикла обслуживания всех станков совершает возвратный переход к первому станку.

При циклическом обслуживании и кольцевом расположении станков возвратные переходы отсутствуют. Следовательно, при количестве станков Н >= 3 и циклическом обслуживании очевидно преимущество кольцевых маршрутов.

При обслуживании двух станков следует располагать оборудование по III варианту планировки, так как в этом случае переходы рабочего от станка к станку отсутствуют.

Если рабочий обслуживает три станка, удобнее располагать оборудование в виде буквы П, так как переходы в этом случае будут наиболее краткими.

При нециклическом обслуживании рабочий по окончании работы на одном из

станков переходит к другому станку, включенному в рабочее место

многостаночника. Среднее расстояние перехода многостаночника от одного

станка к другому (А , м) можно определить по формуле:

ср

Н – 2

А = а x (1 + ——-), (3.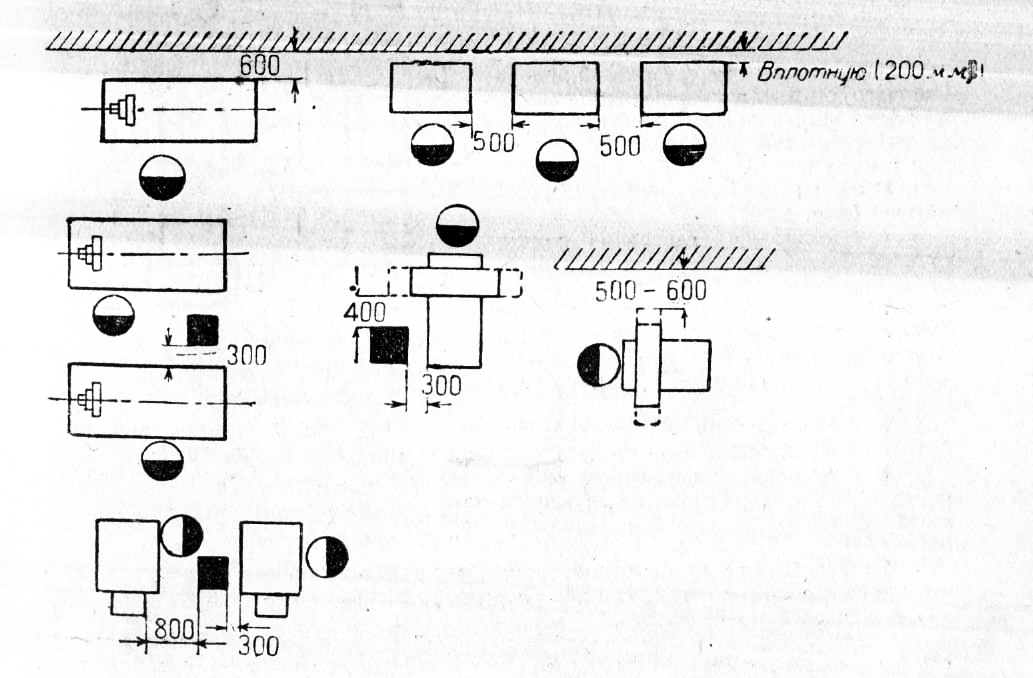 6)

ср ср 3

где а – среднее расстояние между двумя соседними станками, м;

ср

Н – число обслуживаемых станков.

В табл. 3.3 приведены затраты времени на перемещение рабочего от станка к станку при многостаночном обслуживании за один цикл по усредненным данным, рассчитанные исходя из следующих условий: среднее расстояние между станками – 2 м, за один цикл рабочий один раз подходит к каждому станку.

Открыть полный текст документа

Многопильный станок ЦМ-120Э(К) – цена, отзывы, характеристики с фото, инструкция, видео

Многопильный станок ЦМ-150Э(К) предназначен для прямолинейной продольной распиловки досок и брусьев в деревообрабатывающих производствах.

Область применения – средние и малые лесопильные предприятия занятые производством обрезных и необрезных пиломатериалов.
Расчётная производительность (при скорости подачи 4 м/мин, длины 6 м, толщина доски 25 мм, высота доски 105 мм, 7 пил) – 24,5 м3/смена.

Конструктивные особенности

• Жёсткая сварная станина устойчивая к вибрациям;
• Расположение пильного вала – нижнее. Конструкция станка обеспечивает установку до 8 дисковых пил. Расстояние между пилами регулируется за счёт специальных втулок;
• Подача материала – вальцовая. Нижние подающие вальцы закреплены неподвижно, верхние подающие вальцы подпружинены имеет возможность настройки в зависимости от толщины заготовки;
• Регулирование скорости подачи – ступенчатое.
• Безопасность работы на станке обеспечивается когтевыми упорами предотвращающие вылет обрабатываемого материала.

Характеристика	ЦМ-150Э (К)
1. Ширина обрабатываемого материала, мм:
– наибольшая	450
– наименьшая	10
2. Толщина обрабатываемого материала:
– наибольшая	150
– наименьшая	20
3. Длина обрабатываемого материала, мм, не менее	840
4. Диаметр пил, мм, наибольший	500
5. Номинальный посадочный диаметр под пилы, мм.	50
6. Скорость резания, м/с.	50
7. Номинальная скорость подачи, м/мин.	0…20
8. Количество пил, шт, не более	8
9. Расстояние между крайними пилами, мм, не более	200
10. Номинальное расстояние от пола до рабочей поверхности стола, мм.	930
11. Норма обслуживания, чел.	2
12. Габаритные размеры станка, мм, не более: длина / ширина / высота	2050/1300/1750
13. Масса станка, не более, кг.	2000
Характеристика электрооборудования
14. Количество электродвигателей, шт.	2
16. Электродвигатель главного привода (пильного вала)
– номинальная мощность	45
– частота вращения, об/мин	1500
16. Электродвигатель привода подачи:
– номинальная мощность, кВт	1,5
синхронная частота вращения, об/мин.	1500

Отзывы о ЦМ-120Э(К):

Отзывов пока нет, но ваш может быть первым.
Оставить отзыв

Планировка рабочих мест многостаночников | Слагаемые ускорения

Рациональная организация многостаночного обслуживания требует правильного размещения производственного оборудования. Все обслуживаемые станки должны находиться в поле зрения многостаночника, расстояние переходов от станка к станку должно быть минимальным, при обработке крупных и тяжелых деталей станки должны располагаться в непосредственной близости друг от друга и от транспортных средств.

На переходы от одного к другому многостаночник иногда затрачивает 30% рабочего времени. Выбор оптимального маршрута переходов и рациональное расположение оборудования позволяют значительно сократить время на такие переходы.

На рис. 5.2 представлены наиболее распространенные варианты планировки рабочих мест и маршрутов многостаночников.

Рис. 5.2. Типовые планировки рабочих мест при многостаночном обслуживании

при циклическом обслуживании варианту I (линейному) соответствует маятниковый маршрут рабочего; вариантам II,IV,V и VI – замкнутый маршрут; в варианте III переходы рабочего отсутствуют. При циклическом обслуживании станков, расположенных линейно, общее расстояние переходов за один цикл А определяют по формуле, А=2а(n-1) , где а – расстояние между двумя соседними станками; n – количество обслуживаемых станков. При циклическом обслуживании и кольцевом расположении станков возвратные переходы отсутствуют; общее расстояние переходов за один цикл составляет А=аn . Следовательно, при n = 3 и циклическом обслуживании очевидно преимущество кольцевых маршрутов.

При нециклическом обслуживании рабочий после окончания работы на одном из станков переходит к другому, требующему обслуживания. В этом случае среднее расстояние перехода от одного станка к другому Аср определяется по формуле

где аср- среднее расстояние между двумя соседними станками.

В табл. 5.1 приведены затраты времени на перемещение рабочего при многостаночном обслуживании, рассчитанные при а = 2 и одном подходе рабочего к каждому станку за один цикл. Из данных таблицы следует, что при циклическом обслуживании вариант IV более рационален, чем варианты IV и особенно I; при обслуживании двух станков наиболее экономичен вариант III, когда переходы рабочего отсутствуют. При нециклическом обслуживании для всех вариантов затрачиваемое на переходы время одинаково. В этом случае удобство обзора обслуживаемого оборудования является определяющим фактором выбора оптимальной планировки рабочего места.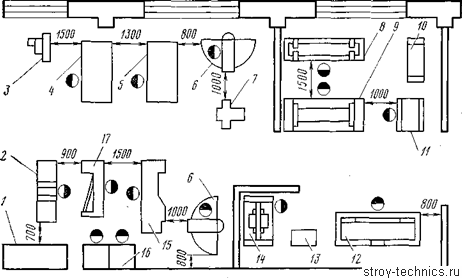 Если рабочий обслуживает небольшое количество станков (до 5), то преимущество имеет вариант I, а при большем количестве (свыше 5) – вариант IV.

Таблица 5.2. Нормативы для планирования развития многостаночного обслуживания в машиностроении при мелкосерийном и единичном производстве

Профессия	Ко.м	Кз.м	Кр.м
Автоматчики Долбежники, протяжчики Заточники Зуборезчики Полировщики, доводчики Резьбонарезчики на специальных станках Резьбошлифовщики Сверловщики Станочники на агрегатных станках Строгальщики Токари Токари-карусельщики Токари-полуавтоматчики Токари-револьверщики Токари-расточники Фрезеровщики Шлифовщики	1,0 0 0,1 0,85 0,4 1,0 0,4 1,0 0,15 0,85 0,2 0,25 1,0 0 0 0,3 0,22	2,75 — 2,0 3,0 2,2 4. 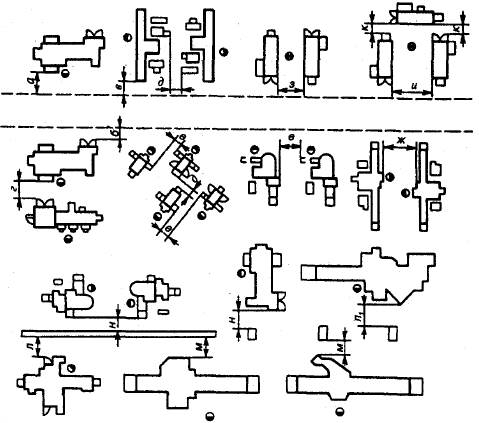0 2,0 2.5 2,3 2.6 2,0 2,2 2,0 — — 2,0 2.1	2,75 — 1,1 2,7 1,5 4,0 1.4 2.5 1,2 2,2 1,2 1,3 2,0 — — 1,3 1,2
Итого:	0,26	2,23	1,32

Продольно-фрезерный станок ССД-5460 Серии ССД-54

СТОЛ

Размер стола	8000х4600	мм
Размеры Т-пазов	28х400	мм
Максимальная допустимая нагрузка на стол (на один метр квадратный)	3000	кг/м2
Расстояние между колоннами	5450	мм

ПЕРЕМЕЩЕНИЯ

Перемещение по оси X	6000	мм
Перемещение по оси Y	5400	мм
Перемещение по оси Z	1100 (1400)	мм

ШПИНДЕЛЬ

Мощность главного двигателя	30/37 (37/45)	кВт
Диапазоны вращения шпинделя	6000	об/мин
Расстояние от торца шпинделя до стола, серия ССД (возможно уменьшение расстояния)	820-1920 (1120-2220)	мм
Конус шпинделя	ISO50 7:24

ПОДАЧИ

Рабочие подачи	1-5000	мм/мин
Ускоренные перемещения X/Y/Z/	6/6/10/	м/мин

МАГАЗИН ИНСТРУМЕНТА

Количество мест	32 (40,60,80,120)	шт
Максимальный вес инструмента	18	кг
Размер инструмента при полном магазине (Ø х длина)	125х350	мм
Размер инструмента при заполнении через гнездо  (Ø х длина)	220х350	мм
Тип инструментального магазина	ВТ50/CAT50

ТОЧНОСТЬ

Точность позиционирования Y, Z	±0,005/300	мм
Точность позиционирования портала, ось X	±0,015/500	мм
Повторяемость Y, Z	±0,0025	мм
Повторяемость, X	±0,008	мм

ПОТРЕБЛЯЕМАЯ МОЩНОСТЬ

Потребляемая мощность

70 (80)

кВт

ГАБАРИТЫ И МАССА

Длина	11000	мм
Ширина	8100	мм
Высота, серия ССД	5100 (5400)	мм
Масса станка, серия ССД	110000	кг

Как рассчитать безопасное расстояние

Для работы большинства промышленного оборудования требуется вмешательство человека.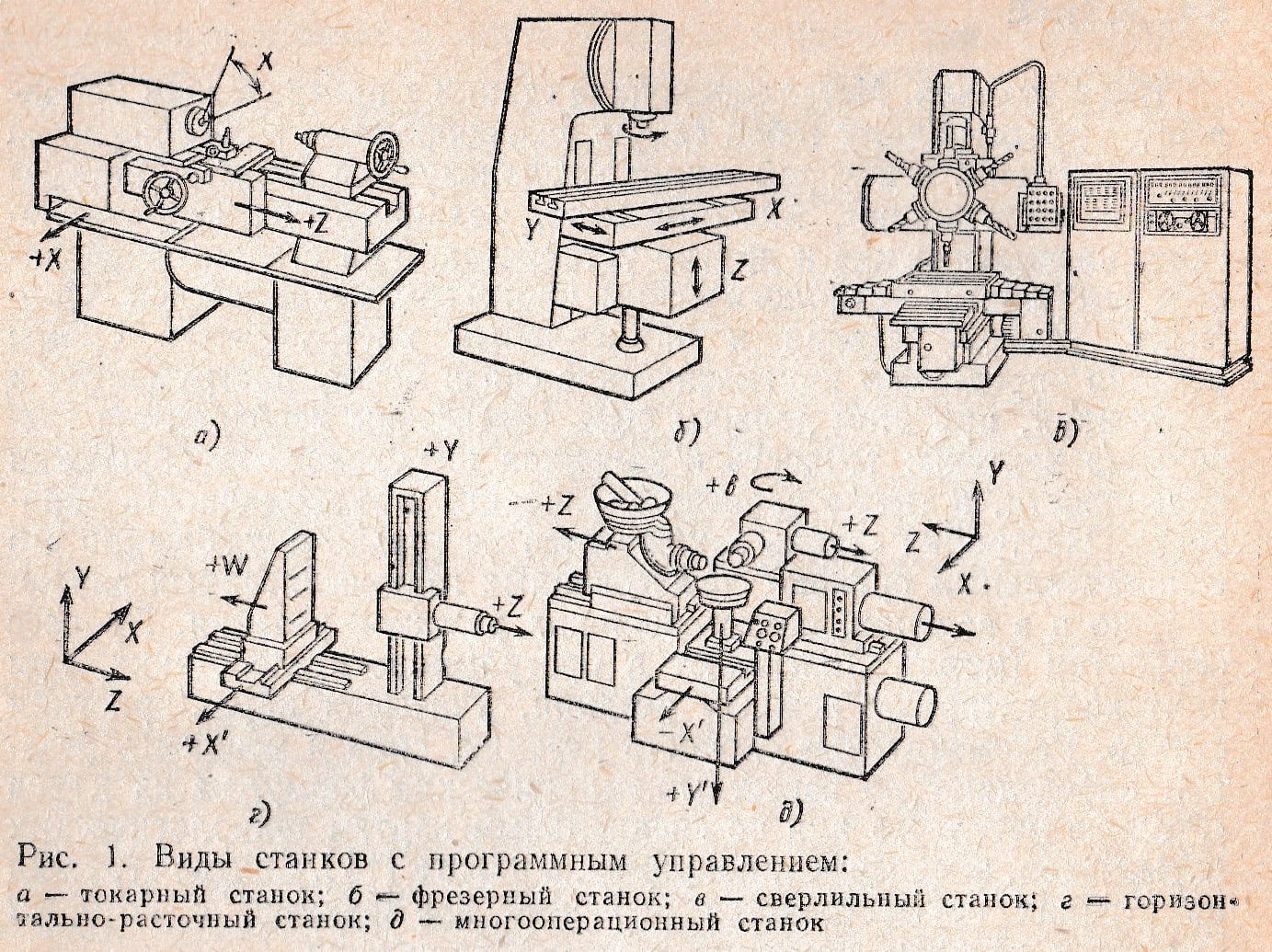 Рабочие должны быть защищены от опасного взаимодействия с машинами. Расчет минимального безопасного монтажного расстояния жизненно важен для обеспечения безопасности рабочего. Кроме того, чрезмерные монтажные расстояния занимают ценную площадь и могут увеличить время, необходимое для обслуживания оборудования, что, в свою очередь, снижает производительность.

Видеоблог

: Расчет безопасного останова Ds = [K x (Ts + Tc + Tr)] + Dpf

Стенограмма видео

Здравствуйте, это Остин Десмонд, специалист по автоматизации Horizon Solutions.Сегодня мы обсудим формулы безопасного монтажного расстояния, а также разницу между ПЛК с рейтингом безопасности и релейным решением с рейтингом безопасности.

При ремонте старого оборудования и создании нового оборудования могут потребоваться такие устройства, как световые завесы и сканеры площадей, а также другие безопасные датчики присутствия. Назначение всех этих устройств – безопасно остановить опасность и привести ее в безопасное состояние до того, как оператор достигнет ее. Хотя безопасная остановка опасных частей оборудования для защиты безопасности рабочих всегда должна быть приоритетом, часто упускаемый из виду, но чрезвычайно важный компонент уравнения – время, которое требуется от срабатывания устройства до достижения машиной безопасного состояния.В этом видео мы подчеркнем разницу в безопасном тормозном пути между реле безопасности и системой управления PLC с рейтингом безопасности.

Вот уравнение для создания безопасного минимального монтажного расстояния: Ds = [K x (Ts + Tc + Tr)] + Dpf, как определено Американским национальным институтом стандартов (ANSI).

• Ds = минимальное безопасное расстояние между предохранительным устройством и опасностью
• K = постоянная скорости; Минимум 1,6 м / сек (63 дюйма / сек), исходя из движения только руки / руки и неподвижного тела
• Ts = время остановки машины / оборудования
• Tc = время остановки системы управления
• Tr = время отклика устройства защиты
• Dpf = максимальное перемещение в направлении опасности в пределах поля защитных устройств с датчиком присутствия (PSSD), которое может произойти до подачи сигнала об остановке. Коэффициенты глубины проникновения будут меняться в зависимости от типа устройства и применения.

Основная причина проведения этих расчетов сегодня – подчеркнуть разницу в безопасном монтажном расстоянии при рассмотрении различных систем управления. Теперь давайте сосредоточимся на релейном решении и решении ПЛК безопасности. Я не хочу углубляться в математику, но хочу сказать, что для обоих расчетов ЕДИНСТВЕННЫЙ главный фактор, который мы собираемся изменить сегодня, – это Tc. Для обоих решений Ts – это время от момента изменения состояния выхода до полной остановки машины.В этом примере мы используем время реакции Tr для световой завесы 15 мс. Коэффициент глубины проникновения был рассчитан с использованием стандартов ANSI. Это будет одинаково для обеих ситуаций. Теперь для реле время отклика самого реле составляет 40 мсек от изменения входа до изменения выхода. Теперь использование Rockwell Automation предоставило инструмент времени реакции GuardLogix® в диапазоне от 20 до 72 мс, учитывая, что время реакции не было обнаружено. Это быстрый снимок этого инструмента. Как видите, с учетом единственной неисправности время реакции 82 мс.Учитывая множественные отказы, что было бы наихудшим сценарием, время отклика составляет 112 мс. На самом деле все это означает, что с помощью релейного решения вы можете установить световую завесу на расстоянии 18 дюймов от источника опасности. С ПЛК опасность должна быть на расстоянии более 20,5 дюймов от световой завесы. Это было рассчитано с использованием единственного отказоустойчивого устройства, и, когда этот расчет обычно выполняется, выполняется сценарий наихудшего случая, при котором безопасное расстояние установки решения ПЛК увеличивается до 23 дюймов, что на целых 5 дюймов дальше, чем реле.

Ссылки и инструменты, упомянутые в видео

В своем видео Остин упоминает несколько ссылок, они приведены ниже…

1. [Ссылка на отметку 2 м 46 с] Инструмент определения времени реакции Rockwell Automation GuardLogix
2. [PDF-файл размером 38 МБ, в частности, Приложение C, начиная со страницы 193] Safety Accelerator Toolkit
3. [Страница с 8 вариантами загрузки для конкретных приложений] Safety Accelerator Toolkit
4. [Информация] Услуги по безопасности через Horizon Solutions

Специалисты Horizon Solutions имеют различные аккредитации по безопасности, включая TUV Functional Safety Tech. Наша команда экспертов по безопасности часто принимает участие в расчетах безопасного расстояния остановки. Horizon Solutions также имеет в штате Авторизованных тренеров OSHA по распространению информации. Нужна помощь? Свяжитесь с нами.

Почему безопасность оборудования важна?

Движущиеся машины могут причинить травмы разными способами:

• Люди могут быть поражены или травмированы движущимися частями оборудования или выброшенным материалом. Части тела также могут быть затянуты или зажаты между роликами, ремнями и шкивными приводами
• Острые края могут стать причиной порезов и рубящих травм, острые части могут нанести удар или прокол кожи, а части с шероховатой поверхностью могут вызвать трение или истирание
• Люди могут быть раздавлены как между частями, движущимися вместе, так и по направлению к неподвижной части машины, стене или другому объекту, а две части, движущиеся друг мимо друга, могут вызвать срезание
• Детали машины, материалы и выбросы (например, пар или вода) могут быть достаточно горячими или холодными, чтобы вызвать ожоги или ожоги, а электричество может вызвать поражение электрическим током и ожоги
• Травмы также могут возникать из-за того, что оборудование становится ненадежным и развиваются неисправности, или когда машины используются ненадлежащим образом из-за неопытности или отсутствия подготовки.

Что мне делать?

Перед тем, как начать

Прежде чем вы начнете использовать какую-либо машину, вам нужно подумать о том, какие риски могут возникнуть и как с ними можно справиться.Поэтому вам следует сделать следующее:

• Убедитесь, что машина укомплектована, оснащены всеми защитными приспособлениями и не имеют дефектов. Термин «защита» включает ограждения, блокировки, двуручные органы управления, световые ограждения, чувствительные к давлению коврики и т. Д. По закону поставщик должен обеспечить надлежащие меры безопасности и информировать покупателей о любых рисках («остаточных рисках»), которые необходимо учитывать пользователям. знать и управлять, потому что они не могут быть разработаны
• Обеспечьте безопасную систему работы для использования и обслуживания машины.При техническом обслуживании может потребоваться проверка критически важных функций, когда их повреждение может вызвать риск. Также обратите внимание на остаточные риски, указанные производителем в информации / инструкциях, прилагаемых к машине, и убедитесь, что они включены в систему безопасности работы
• Убедитесь, что каждая статическая машина установлена ​​правильно и устойчива (обычно зафиксирована).
• Выберите подходящую машину для работы и не размещайте машины там, где клиенты или посетители могут подвергаться риску
• Обратите внимание, что новые машины должны иметь маркировку CE и поставляться с Декларацией соответствия и инструкциями на английском языке.

Убедитесь, что машина:

• безопасен для любых работ, которые должны быть выполнены при настройке, при нормальной эксплуатации, при устранении засоров, при ремонте поломок и во время планового обслуживания
• должным образом выключен, изолирован или заблокирован, прежде чем предпринимать какие-либо действия по устранению засоров, чистке или регулировке машины

Также убедитесь, что вы выявляете и устраняете риски от:

• электрические, гидравлические или пневматические источники питания
• плохо спроектированные предохранительные устройства.Это может быть неудобно в использовании или легко отменяется, что может побудить ваших рабочих рискнуть получить травму и нарушить закон. Если да, выясните, почему они это делают, и примите соответствующие меры для устранения причин / причин

Предотвращение доступа к опасным частям

Подумайте, как сделать машину безопасной. Меры, которые вы используете для предотвращения доступа к опасным частям, должны быть в следующем порядке. В некоторых случаях может потребоваться сочетание этих мер:

• По возможности используйте фиксированные ограждения (например, закрепленные винтами или гайками и болтами) для ограждения опасных частей.Используйте лучший материал для этих ограждений – пластик может быть хорошо виден, но его легко повредить. Если вы используете проволочную сетку или аналогичные материалы, убедитесь, что отверстия недостаточно велики, чтобы обеспечить доступ к движущимся частям
  
• Если фиксированные ограждения нецелесообразны, используйте другие методы, например, заблокируйте ограждение, чтобы машина не могла запуститься до закрытия ограждения и не могла быть открыта, пока машина все еще движется. В некоторых случаях можно использовать системы отключения, такие как фотоэлектрические устройства, чувствительные к давлению маты или автоматические ограждения, если другие ограждения не подходят.
  
• Если ограждения не могут обеспечить полную защиту, используйте приспособления, держатели, толкатели и т. Д., Если это целесообразно.
  
• Управляйте любым остающимся риском, предоставляя оператору необходимую информацию, инструкции, обучение, надзор и соответствующее защитное оборудование

Пример использования

Компания была привлечена к уголовной ответственности после того, как рабочий получил ужасные травмы, чуть не отрубив левую руку при использовании торцовочной пилы.

Что стало причиной аварии?

Носовая защита была установлена ​​неправильно из-за недостаточной подготовки. У рабочего не было предыдущего опыта, и он обучался работе с пилой всего 5 минут. Сюда не входило никаких инструкций о защитных кожухах пилы и о том, как их правильно отрегулировать. К тому же пила была непригодна для тренировочных целей.

Другие вещи, на которые следует обратить внимание

• Если машины управляются программируемыми электронными системами, изменения любых программ должны выполняться компетентным лицом (лицом, обладающим необходимыми навыками, знаниями и опытом для безопасного выполнения работ).Записывайте такие изменения и проверяйте их правильность.
• Убедитесь, что переключатели управления четко обозначены, чтобы показать, что они делают.
• При необходимости иметь органы управления аварийной остановкой, например кнопки с грибовидными головками в пределах легкой досягаемости
• Убедитесь, что элементы управления спроектированы и размещены таким образом, чтобы исключить случайное нажатие и травмы, при необходимости используйте средства управления двумя руками, а также кнопки запуска кожуха и педали.
• Не позволяйте неуполномоченным, неквалифицированным или неподготовленным людям использовать оборудование – никогда не позволяйте детям управлять машинами или помогать им.Некоторые работники, например новички, молодые люди или инвалиды, могут подвергаться особому риску и нуждаться в инструктаже, обучении и надзоре
• Соответствующее обучение должно гарантировать, что те, кто использует тренажер, обладают достаточной квалификацией для безопасного использования. Это включает обеспечение наличия у них необходимых навыков, знаний и опыта – иногда требуется формальная квалификация, например, для операторов бензопилы
• Чтобы быть эффективными, руководители также должны быть надлежащим образом обучены и компетентны.Им может потребоваться дополнительное специальное обучение, и существуют признанные курсы для руководителей
• Убедитесь, что рабочая зона вокруг станка содержится в чистоте и порядке, не имеет препятствий, поскользнулся и спотыкается, а также хорошо освещена.

Правила техники безопасности для рабочих

Do…

• проверить, что машина находится в хорошем состоянии и пригодна для использования, т. Е. Подходит для работы и работает должным образом, и что все меры безопасности приняты – ограждения, изоляторы, запорные механизмы, аварийные выключатели и т. Д.
• используйте машину правильно и в соответствии с инструкциями производителя
• убедитесь, что вы носите соответствующую защитную одежду и оборудование, необходимые для этой машины, такие как защитные очки, средства защиты слуха и защитную обувь.

Не надо…

• использовать машину или прибор, на котором есть знак опасности или бирка.Знаки опасности должны удаляться только уполномоченным лицом, которое убеждено, что машина или процесс теперь безопасны.
• Носить свисающие цепи, свободную одежду, кольца или иметь распущенные длинные волосы, которые могут попасть в движущиеся части
• отвлекают людей использующих машины
• удалите любые защитные приспособления, даже если их присутствие затрудняет работу

Узнать больше

Сайт оборудования и техники НИУ ВШЭ

Закон

Положения о предоставлении и использовании рабочего оборудования 1998 (PUWER)

Работа с машинами: ответы по охране труда

Следующий контрольный список поможет определить опасности на вашем рабочем месте. Важно адаптировать информацию к вашему рабочему месту и при необходимости добавлять любые дополнительные элементы.

9019 9019 Определите, где рабочий может контактировать с частями, движущимися с высокой скоростью (например,g. , опасность истирания или трения)

Возможная опасность	Check One		Примечания
	OK	Требуется исследование
Станок
Определите использование и пределы производственного цикла станка 902 с учетом: 97 раз предполагаемое использование станка используемых материалов создаваемых сил диапазон движения движущихся частей
Определите, сколько места необходимо машине для безопасной работы все задач, выполняемых на машине и на машине, включая доступ для обслуживания и ремонта.
Определите ожидаемый срок службы деталей и жидкостей в результате износа
Определите пределы окружающей среды машины (например, рабочие температуры, влажность, шум и т. д.)
Подумайте, как машина взаимодействует с другими машинами, оборудованием и источниками энергии
Рассмотрите все задачи, которые машина выполняет и на которых выполняется машина во время эксплуатации пробные прогоны регулярная работа замена инструмента плановое обслуживание устранение заклинивания и восстановление после сбоев внеплановое обслуживание
Рассмотрение связанных задач с диф различные фазы жизни машины запуск и программирование загрузка, упаковка, транспортировка, распаковка вывод из эксплуатации и утилизация
Механические компоненты
точки действия, определите следующее: какие части движутся диапазон движения движущихся частей тип движения (например,g. , вращение, резка, гибка, резка, штамповка) Примечание – рабочая точка относится к той области станка, где выполняется полезная работа. Обычно в этой точке оператор контактирует с машиной.
Определите, как мощность передается на машину гидравлическая пневматическая механическая
, если есть тормоз, укажите или сцепления, и как оно работает
Определите все «рабочие точки зажима» на машине
Определите все точки защемления на машине
Определите опасность зацепления машины в результате контакта с: вращающимися и движущимися частями движущимися материалами выступами или зазорами
Определите опасности порезов или отрезания, где рабочий может соприкоснуться с режущими инструментами, пилами, фрезерными станками, ножами или острыми предметами
Определите опасность порезов, когда рабочий может быть серьезно порезан, находясь между двумя частями машины или между частью машины и заготовкой или неподвижным объектом
Определите опасность раздавливания, когда рабочий может быть зажат между ними части машины, движущиеся друг против друга
Определите, возможно ли получить удар или прокол летящими объектами
Проверьте работу машины, чтобы определить, работает ли рабочий может контактировать с жидкостями под давлением или газы
Определите любые острые кромки и угловые детали, которые выступают (выступают) из машины
Определите ситуации, при которых может произойти повреждение в случае неисправности или поломка машины или материала (точка поломки)
Определите ситуации, в которых может произойти повреждение, если операционное программное обеспечение машины (если применимо) выйдет из строя.
Особенности рабочего
Определите всю работу, которую рабочий должен выполнять во время работы на машине, в том числе: , как материал загружается в машину как конечный продукт снято с машины удаление лома периодическая очистка точки входа и других частей машины проверки безопасности перед сменой
Определите все работы, которые необходимо выполнить при выполнении технического обслуживания
Определите все работы, которые необходимо выполнить для замены инструмента или матрицы
Определите любую потенциальную опасность скольжения или падения внутри и вокруг машины как результат поверхности пола , или из-за разливов материалов (например,(смазочные масла, консистентная смазка, вода, опилки, пластиковые гранулы)
Определите другие возможные опасности, например, вибрацию или шум
Определите потенциальные проблемы с эргономикой в эксплуатации машины. Убедитесь, что: рабочий не должен слишком сильно тянуться рабочий не должен использовать чрезмерную силу рабочий не должен выполнять высокочастотные движения рабочий цикл основан на мощности рабочего, а не наоборот рабочий может выполнять работу в нескольких положениях, которые обеспечивают нейтральное положение тела рабочая поверхность регулируется рабочий имеет достаточно места, чтобы двигаться, ничего не нанося ударов

4 Дистанционные измерения для машинного обучения

Последнее обновление 19 августа 2020 г.

Измерения расстояния играют важную роль в машинном обучении.

Они обеспечивают основу для многих популярных и эффективных алгоритмов машинного обучения, таких как k-ближайшие соседи для обучения с учителем и кластеризация по k-средним для обучения без учителя.

В зависимости от типа данных необходимо выбирать и использовать различные меры расстояния. Таким образом, важно знать, как реализовать и рассчитать ряд различных популярных мер расстояния, а также интуитивно понимать итоговые оценки.

В этом руководстве вы откроете для себя меры расстояния в машинном обучении.

После прохождения этого руководства вы будете знать:

• Роль и важность дистанционных измерений в алгоритмах машинного обучения.
• Как реализовать и вычислить меры расстояния Хэмминга, Евклида и Манхэттена.
• Как реализовать и вычислить расстояние Минковского, которое обобщает меры евклидова и манхэттенского расстояния.

Начните свой проект с моей новой книги «Мастерство машинного обучения с Python», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.

Приступим.

Меры расстояния для машинного обучения
Фото принца Роя, некоторые права защищены.

Обзор учебного пособия

Это руководство разделено на пять частей; их:

1. Роль дистанционных мер
2. Расстояние Хэмминга
3. Евклидово расстояние
4. Расстояние до Манхэттена (такси или городской квартал)
5. Минковский Дистанция

Роль дистанционных мер

Измерения расстояния играют важную роль в машинном обучении.

Измерение расстояния – это объективная оценка, которая суммирует относительную разницу между двумя объектами в проблемной области.

Чаще всего эти два объекта представляют собой строки данных, которые описывают предмет (например, человека, машину или дом) или событие (например, покупку, претензию или диагноз).

Возможно, наиболее вероятно, что вы столкнетесь с измерением расстояния, когда вы используете определенный алгоритм машинного обучения, который в своей основе использует меры расстояния. Самый известный алгоритм этого типа – алгоритм k-ближайших соседей, или сокращенно KNN.

В алгоритме KNN для новых примеров выполняется прогнозирование классификации или регрессии путем вычисления расстояния между новым примером (строкой) и всеми примерами (строками) в наборе обучающих данных. Затем выбираются k примеров в наборе обучающих данных с наименьшим расстоянием, и делается прогноз путем усреднения результата (режим метки класса или среднего реального значения для регрессии).

KNN принадлежит к более широкой области алгоритмов, называемых обучением на основе случаев или экземпляров, большинство из которых аналогичным образом используют меры расстояния.Другой популярный алгоритм на основе экземпляров, который использует меры расстояния, – это алгоритм квантования вектора обучения, или LVQ, алгоритм, который также может считаться типом нейронной сети.

Связанный – это алгоритм самоорганизующейся карты, или SOM, который также использует меры расстояния и может использоваться для обучения с учителем или без него. Другой алгоритм обучения без учителя, в основе которого лежат меры расстояния, – это алгоритм кластеризации K-средних.

При обучении на основе экземпляров обучающие примеры сохраняются дословно, а функция расстояния используется для определения того, какой член обучающего набора наиболее близок к неизвестному экземпляру теста.После обнаружения ближайшего обучающего экземпляра прогнозируется его класс для тестового экземпляра.

– стр. 135, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г.

Краткий список некоторых из наиболее популярных алгоритмов машинного обучения, в основе которых лежит измерение расстояния, выглядит следующим образом:

• К-Ближайшие соседи
• Обучающее векторное квантование (LVQ)
• Самоорганизующаяся карта (SOM)
• Кластеризация K-средних

Есть много методов, основанных на ядре, которые также могут считаться алгоритмами на основе расстояния.Возможно, наиболее широко известный метод ядра – это алгоритм машины опорных векторов, или сокращенно SVM.

Знаете ли вы другие алгоритмы, использующие меры расстояния?
Дайте мне знать в комментариях ниже.

При вычислении расстояния между двумя примерами или строками данных возможно, что для разных столбцов примеров используются разные типы данных. В примере могут быть реальные значения, логические значения, категориальные значения и порядковые значения. Для каждого могут потребоваться разные меры расстояния, которые суммируются в единую оценку расстояния.

Числовые значения могут иметь разные масштабы. Это может сильно повлиять на расчет меры расстояния, и часто рекомендуется нормализовать или стандартизировать числовые значения до расчета меры расстояния.

Числовая ошибка в задачах регрессии также может считаться расстоянием. Например, ошибка между ожидаемым значением и прогнозируемым значением – это одномерная мера расстояния, которую можно суммировать или усреднить по всем примерам в тестовом наборе, чтобы получить общее расстояние между ожидаемыми и прогнозируемыми результатами в наборе данных. Расчет ошибки, такой как среднеквадратическая ошибка или средняя абсолютная ошибка, может напоминать стандартную меру расстояния.

Как мы видим, меры расстояния играют важную роль в машинном обучении. Пожалуй, четыре наиболее часто используемых показателя расстояния в машинном обучении следующие:

• Расстояние Хэмминга
• Евклидово расстояние
• Манхэттен Расстояние
• Минковский Дистанция

Какие еще меры расстояния вы использовали или о которых слышали?
Дайте мне знать в комментариях ниже.

Вам необходимо знать, как вычислять каждую из этих мер расстояния при реализации алгоритмов с нуля, и интуитивно понимать, что именно вычисляется при использовании алгоритмов, использующих эти меры расстояния.

Давайте рассмотрим каждый по очереди.

Расстояние Хэмминга

Расстояние Хэмминга вычисляет расстояние между двумя двоичными векторами, также называемыми двоичными строками или для краткости строками битов.

Вы, скорее всего, столкнетесь с битовыми строками, когда будете горячо кодировать категориальные столбцы данных.

Например, если столбец имеет категории « красный », « зеленый » и « синий », вы можете по одному горячему кодировать каждый пример как битовую строку с одним битом для каждого столбца.

• красный = [1, 0, 0]
• зеленый = [0, 1, 0]
• синий = [0, 0, 1]

Расстояние между красным и зеленым можно рассчитать как сумму или среднее количество разностей битов между двумя цепочками битов. Это расстояние Хэмминга.

Для строки с горячим кодированием, возможно, имеет смысл суммировать сумму разностей битов между строками, которая всегда будет равна 0 или 1.

• Расстояние Хэмминга = сумма от i до N абс (v1 [i] – v2 [i])

Для цепочек битов, которые могут иметь много 1 битов, чаще всего вычисляют среднее количество разностей битов, чтобы получить оценку расстояния Хэмминга между 0 (идентично) и 1 (все разные).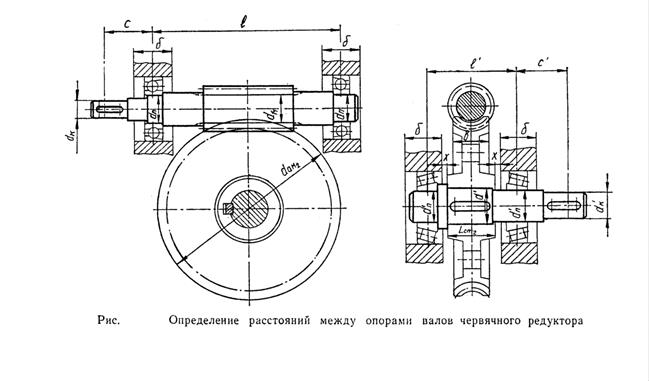

• Расстояние Хэмминга = (сумма от i до N абс (v1 [i] – v2 [i])) / N

Мы можем продемонстрировать это на примере вычисления расстояния Хэмминга между двумя цепочками битов, перечисленных ниже.

# вычисляем расстояние Хэмминга между битовыми строками # вычислить расстояние Хэмминга def hamming_distance (a, b): возврат суммы (abs (e1 – e2) для e1, e2 в zip (a, b)) / len (a) # определить данные row1 = [0, 0, 0, 0, 0, 1] row2 = [0, 0, 0, 0, 1, 0] # вычислить расстояние dist = hamming_distance (строка1, строка2) печать (расстояние)

# вычисление расстояния Хэмминга между битовыми строками # Расчет расстояния Хэмминга def hamming_distance (a, b): возвращаемая сумма (abs (e1 – e2) для e1, e2 в zip (a, b)) / len (a) # определить данные row1 = [0, 0, 0, 0, 0, 1] row2 = [0, 0, 0, 0, 1, 0] # вычислить расстояние dist = hamming_distance (row1, row2) print (dist)

При выполнении примера отображается расстояние Хэмминга между двумя цепочками битов.

Мы видим, что есть два различия между строками, или 2 из 6 битовых позиций, которые в среднем (2/6) составляют примерно 1/3 или 0,333.

Мы также можем выполнить те же вычисления, используя функцию hamming () из SciPy. Полный пример приведен ниже.

# вычисляем расстояние Хэмминга между битовыми строками из scipy.spatial.distance import hamming # определить данные row1 = [0, 0, 0, 0, 0, 1] row2 = [0, 0, 0, 0, 1, 0] # вычислить расстояние dist = hamming (row1, row2) печать (расстояние)

# вычисление расстояния Хэмминга между битовыми строками от scipy.пространственное расстояние import hamming # определить данные row1 = [0, 0, 0, 0, 0, 1] row2 = [0, 0, 0, 0, 1, 0] # вычислить расстояние расстояние = Hamming (row1, row2) print (dist)

Запустив пример, мы видим, что получаем тот же результат, что подтверждает нашу ручную реализацию.

Евклидово расстояние

Евклидово расстояние вычисляет расстояние между двумя векторами с действительными значениями.

Вы, скорее всего, будете использовать евклидово расстояние при вычислении расстояния между двумя строками данных, которые имеют числовые значения, такие как значения с плавающей запятой или целые числа.

Если столбцы имеют значения с разными масштабами, принято нормализовать или стандартизировать числовые значения во всех столбцах перед вычислением евклидова расстояния. В противном случае столбцы с большими значениями будут доминировать при измерении расстояния.

Хотя есть и другие возможные варианты, большинство учащихся на основе экземпляров используют евклидово расстояние.

– стр. 135, Интеллектуальный анализ данных: практические инструменты и методы машинного обучения, 4-е издание, 2016 г.

Евклидово расстояние вычисляется как квадратный корень из суммы квадратов разностей между двумя векторами.2

Это вычисление связано с векторной нормой L2 и эквивалентно квадрату ошибки суммы и квадрату ошибки корня суммы квадрата, если квадратный корень добавлен.

Мы можем продемонстрировать это на примере вычисления евклидова расстояния между двумя действительными векторами, перечисленными ниже.

# вычисляем евклидово расстояние между векторами из математического импорта sqrt # вычислить евклидово расстояние def euclidean_distance (a, b): return sqrt (sum ((e1-e2) ** 2 для e1, e2 в zip (a, b))) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = euclidean_distance (строка1, строка2) печать (расстояние)

# вычисление евклидова расстояния между векторами from math import sqrt # вычисление евклидова расстояния def euclidean_distance (a, b): return sqrt (sum ((e1-e2) ** 2 for e1, e2 в zip (a, b))) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = euclidean_distance (row1, row2) print (dist)

При выполнении примера отображается евклидово расстояние между двумя векторами.

Мы также можем выполнить те же вычисления, используя функцию euclidean () из SciPy. Полный пример приведен ниже.

# вычисляем евклидово расстояние между векторами from scipy.spatial.distance import euclidean # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = евклидово (строка1, строка2) печать (расстояние)

# вычисление евклидова расстояния между векторами из scipy.пространственное расстояние импорт евклидова # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = евклидово (row1, row2) печать (расст.)

Запустив пример, мы видим, что получаем тот же результат, что подтверждает нашу ручную реализацию.

Манхэттенское расстояние (такси или городское расстояние)

Манхэттенское расстояние, также называемое расстоянием такси или расстоянием городского квартала, вычисляет расстояние между двумя векторами с действительными значениями.

Возможно, это более полезно для векторов, которые описывают объекты на единой сетке, например, шахматную доску или городские кварталы. Название такси для меры относится к интуитивному пониманию того, что рассчитывает мера: кратчайший путь, по которому такси может пройти между городскими кварталами (координаты на сетке).

Может иметь смысл вычислить манхэттенское расстояние вместо евклидова расстояния для двух векторов в целочисленном пространстве признаков.

Манхэттенское расстояние рассчитывается как сумма абсолютных разностей между двумя векторами.

• ManhattanDistance = сумма от i до N сумма | v1 [i] – v2 [i] |

Манхэттенское расстояние связано с векторной нормой L1 и суммарной абсолютной ошибкой и показателем средней абсолютной ошибки.

Мы можем продемонстрировать это на примере вычисления манхэттенского расстояния между двумя целочисленными векторами, перечисленными ниже.

# вычисление манхэттенского расстояния между векторами из математического импорта sqrt # вычислить манхэттенское расстояние def manhattan_distance (a, b): возврат суммы (abs (e1-e2) для e1, e2 в zip (a, b)) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = расстояние_манхэттена (строка1, строка2) печать (расстояние)

# вычисление манхэттенского расстояния между векторами from math import sqrt # вычисление манхэттенского расстояния def manhattan_distance (a, b): return sum (abs (e1-e2) for e1, e2 in zip ( a, b)) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = manhattan_distance (row1, row2) print (dist)

При выполнении примера отображается манхэттенское расстояние между двумя векторами.

Мы также можем выполнить тот же расчет, используя функцию cityblock () из SciPy. Полный пример приведен ниже.

# вычисление манхэттенского расстояния между векторами из scipy.spatial.distance import cityblock # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = cityblock (row1, row2) печать (расстояние)

# вычисление манхэттенского расстояния между векторами из scipy.пространственное расстояние import cityblock # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние dist = cityblock (row1, row2) печать (расст.)

Запустив пример, мы видим, что получаем тот же результат, что подтверждает нашу ручную реализацию.

Минковский Дистанция

Расстояние Минковского вычисляет расстояние между двумя векторами с действительными значениями.(1 / п)

Где « p » – параметр порядка.

Если для p установлено значение 1, расчет аналогичен манхэттенскому расстоянию. Когда p установлено на 2, это то же самое, что и евклидово расстояние.

• p = 1 : Манхэттенское расстояние.
• p = 2 : Евклидово расстояние.

Промежуточные значения обеспечивают контролируемый баланс между двумя показателями.

Обычно используется расстояние Минковского при реализации алгоритма машинного обучения, который использует меры расстояния, поскольку он дает контроль над типом меры расстояния, используемой для векторов с действительным знаком, через гиперпараметр « p », который можно настраивать.

Мы можем продемонстрировать этот расчет на примере вычисления расстояния Минковского между двумя действительными векторами, перечисленными ниже.

# вычисление расстояния Минковского между векторами из математического импорта sqrt # вычислить расстояние Минковского def minkowski_distance (a, b, p): return sum (abs (e1-e2) ** p for e1, e2 in zip (a, b)) ** (1 / p) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние (p = 1) dist = minkowski_distance (строка1, строка2, 1) печать (расстояние) # вычислить расстояние (p = 2) dist = minkowski_distance (строка1, строка2, 2) печать (расстояние)

# вычисление расстояния Минковского между векторами from math import sqrt # вычисление расстояния Минковского def minkowski_distance (a, b, p): return sum (abs (e1-e2) ** p for e1 , e2 в zip (a, b)) ** (1 / p) # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние (p = 1) dist = minkowski_distance (row1, row2, 1) print (dist) # вычислить расстояние (p = 2) dist = minkowski_distance (row1, row2, 2) печать (расст.)

При выполнении примера сначала вычисляется и печатается расстояние Минковского с p, установлено на 1, чтобы дать манхэттенское расстояние, затем с p, установлено на 2, чтобы дать евклидово расстояние, совпадающее со значениями, вычисленными на тех же данных из предыдущих разделов .

Мы также можем выполнить те же вычисления, используя функцию minkowski_distance () из SciPy. Полный пример приведен ниже.

# вычисление расстояния Минковского между векторами из scipy.spatial импорт minkowski_distance # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние (p = 1) dist = minkowski_distance (строка1, строка2, 1) печать (расстояние) # вычислить расстояние (p = 2) dist = minkowski_distance (строка1, строка2, 2) печать (расстояние)

# вычисление расстояния Минковского между векторами из scipy.пространственный импорт minkowski_distance # определить данные row1 = [10, 20, 15, 10, 5] row2 = [12, 24, 18, 8, 7] # вычислить расстояние (p = 1) dist = minkowski_distance (row1, row2, 1) print (dist) # вычислить расстояние (p = 2) dist = minkowski_distance (row1, row2, 2) print (dist)

Запустив пример, мы видим, что получаем те же результаты, что подтверждает нашу ручную реализацию.

Дополнительная литература

Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.

Книги

API

Статьи

Сводка

В этом руководстве вы открыли для себя меры расстояния в машинном обучении.

В частности, вы выучили:

• Роль и важность дистанционных измерений в алгоритмах машинного обучения.
• Как реализовать и вычислить меры расстояния Хэмминга, Евклида и Манхэттена.
• Как реализовать и вычислить расстояние Минковского, которое обобщает меры евклидова и манхэттенского расстояния.

Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.

Откройте для себя быстрое машинное обучение на Python!

Разрабатывайте собственные модели за считанные минуты

… всего несколько строк кода scikit-learn

Узнайте, как это сделать, в моей новой электронной книге:
Мастерство машинного обучения с Python

Охватывает руководств для самообучения и сквозные проекты , например:
Загрузка данных , визуализация , моделирование , настройка и многое другое…

: наконец, машинное обучение в

Ваши собственные проекты

Пропустить академики. Только результаты.

Посмотрите, что внутри

метрик расстояния | Различные метрики расстояния в машинном обучении

Метрики расстояния являются ключевой частью нескольких алгоритмов машинного обучения. Эти метрики расстояния используются как в обучении с учителем, так и в обучении без учителя, как правило, для вычисления сходства между точками данных.

Эффективный показатель расстояния повышает производительность нашей модели машинного обучения, будь то задачи классификации или кластеризации.

Допустим, мы хотим создать кластеры с помощью алгоритма кластеризации K-средних или алгоритма k-ближайшего соседа для решения задачи классификации или регрессии. Как вы здесь определите сходство между разными наблюдениями? Как можно сказать, что две точки похожи друг на друга?

Это произойдет, если их функции будут похожи, не так ли? Когда мы наносим эти точки на график, они будут ближе друг к другу на расстоянии.

Следовательно, мы можем вычислить расстояние между точками, а затем определить сходство между ними.Возникает вопрос на миллион долларов: как рассчитать это расстояние и каковы разные показатели расстояния в машинном обучении?

Это то, на что мы стремимся ответить в этой статье. Мы рассмотрим 4 типа показателей расстояния в машинном обучении и поймем, как они работают в Python.

4 типа показателей расстояния в машинном обучении

1. Евклидово расстояние
2. Манхэттен Расстояние
3. Минковский Дистанция
4. Расстояние Хэмминга

Начнем с наиболее часто используемой метрики расстояния – евклидова расстояния.

1. Евклидово расстояние

Евклидово расстояние представляет собой кратчайшее расстояние между двумя точками.

Большинство алгоритмов машинного обучения, включая K-средние, используют этот показатель расстояния для измерения сходства между наблюдениями. Допустим, у нас есть две точки, как показано ниже:

Итак, евклидово расстояние между этими двумя точками A и B будет:

Вот формула евклидова расстояния:

Мы используем эту формулу, когда имеем дело с двумя измерениями.Мы можем обобщить это для n-мерного пространства как:

Где,

• n = количество размеров
• пи, qi = точки данных

Давайте закодируем евклидово расстояние в Python. Это даст вам лучшее понимание того, как работает этот показатель расстояния.

Сначала мы импортируем необходимые библиотеки. Я буду использовать библиотеку SciPy, которая содержит заранее написанные коды для большинства функций расстояния, используемых в Python:

Это две точки выборки, которые мы будем использовать для вычисления различных функций расстояния.Давайте теперь вычислим евклидово расстояние между этими двумя точками:

Вот как мы можем вычислить евклидово расстояние между двумя точками в Python. Давайте теперь разберемся со вторым показателем расстояния, манхэттенским расстоянием.

2. Манхэттен Дистанция

Манхэттенское расстояние – это сумма абсолютных разностей между точками по всем измерениям.

Мы можем представить расстояние до Манхэттена как:

Поскольку приведенное выше представление является двухмерным, для вычисления Манхэттенского расстояния мы возьмем сумму абсолютных расстояний как по осям x, так и по y.Итак, расстояние Манхэттена в двухмерном пространстве определяется как:

И обобщенная формула для n-мерного пространства имеет вид:

Где,

• n = количество размеров
• пи, qi = точки данных

Теперь мы рассчитаем Манхэттенское расстояние между двумя точками:

Обратите внимание, что расстояние Manhattan Distance также известно как расстояние городского квартала. В SciPy есть функция под названием cityblock , которая возвращает Манхэттенское расстояние между двумя точками.

Давайте теперь посмотрим на следующую метрику расстояния – расстояние Минковского.

3. Минковского Дистанция

Расстояние Минковского – это обобщенная форма евклидова и манхэттенского расстояния.

Формула для расстояния Минковского имеет следующий вид:

Здесь p представляет порядок нормы. Рассчитаем расстояние Минковского порядка 3:

.

Параметр p метрики расстояния Минковского в SciPy представляет порядок нормы.Когда порядок (p) равен 1, он будет представлять манхэттенское расстояние, а когда порядок в приведенной выше формуле равен 2, он будет представлять евклидово расстояние.

Давайте проверим, что в Python:

Здесь вы можете видеть, что когда порядок равен 1, расстояние Минковского и Манхэттенское расстояние одинаковы. Давайте проверим также евклидово расстояние:

Когда порядок равен 2, мы видим, что расстояния Минковского и Евклидовы одинаковы.

До сих пор мы рассмотрели метрики расстояния, которые используются, когда мы имеем дело с непрерывными или числовыми переменными.Но что, , если у нас есть категориальные переменные? Как мы можем определить сходство между категориальными переменными? Здесь мы можем использовать другую метрику расстояния, называемую расстоянием Хэмминга.

4. Расстояние Хэмминга

Расстояние Хэмминга измеряет сходство двух строк одинаковой длины. Расстояние Хэмминга между двумя строками одинаковой длины – это количество позиций, на которых соответствующие символы различаются.

Давайте разберемся в концепции на примере.Допустим, у нас есть две строки:

«евклидово» и «манхэттенское»

Поскольку длины этих строк равны, мы можем вычислить расстояние Хэмминга. Мы будем идти по символам и сопоставлять строки. Первый символ обеих строк (e и m соответственно) разный. Точно так же второй символ обеих строк (u и a) отличается. и так далее.

Посмотрите внимательно – семь символов разные, тогда как два символа (последние два символа) похожи:

Следовательно, расстояние Хэмминга здесь будет равно 7.Обратите внимание, что чем больше расстояние Хэмминга между двумя струнами, тем более непохожими будут эти струны (и наоборот).

Давайте посмотрим, как мы можем вычислить расстояние Хэмминга двух строк в Python. Сначала мы определим две строки, которые мы будем использовать:

Это две строки «евклидова» и «манхэттен», которые мы также видели в примере. Давайте теперь вычислим расстояние Хэмминга между этими двумя строками:

Как мы видели в примере выше, расстояние Хэмминга между «евклидовым» и «манхэттенским» равно 7.Мы также видели, что расстояние Хэмминга работает только тогда, когда у нас есть строки одинаковой длины.

Давайте посмотрим, что происходит, когда у нас есть строки разной длины:

Вы можете видеть, что длины обеих струн различаются. Давайте посмотрим, что произойдет, когда мы попытаемся вычислить расстояние Хэмминга между этими двумя строками:

Это вызывает ошибку о том, что длины массивов должны быть одинаковыми. Следовательно, расстояние Хэмминга работает только тогда, когда у нас есть строки или массивы одинаковой длины.

Это некоторые из мер сходства или матриц расстояний, которые обычно используются в машинном обучении.

Связанные

Надежные статистические дистанции для машинного обучения

Разработка мощных алгоритмов обнаружения выбросов и аномалий требует использования правильных инструментов. Узнайте, как могут помочь надежные статистические расстояния.

---

Равномерное (0, 1) Равномерное (-1, 0) Нормальное (0, 1) Нормальное (-1, 0,5) Нормальное (1, 0.5) Бета (2, 2) Бета (1,7, 2,16) Гамма (1, 1) Гамма (2, 0,5) F (10, 10) F (5, 10) F (10, 3) t Стьюдента Генеративное экстремальное значение Парето (2,5 ) Бимодальный (3) Бимодальный (4)

Однородный (0, 1) Однородный (-1, 0) Нормальный (0, 1) Нормальный (-1, 0,5) Нормальный (1, 0,5) Бета (2, 2) Бета (1,7, 2,16) Гамма (1, 1) Гамма (2, 0,5) F (10, 10) F (5, 10) F (10, 3) t Стьюдента Генеративное экстремальное значение Парето (2,5) Бимодальный (3) Бимодальный (4)

График QQ

CDF

Расстояние Колмогорова-Смирнова

–

Расстояние земного движителя

–

Расстояние Крамера-фон Мизеса

–

---

Нормальные распределения Равномерные распределения Бета-дистрибутивы Гамма-распределения Распределение с отбойником Распределение с дальней шишкой Распределения с длинными хвостами Распределения с более длинными хвостами Нормальный (0, 1) vs.Нормальный (0, 1) Нормальный (0, 1) по сравнению со студентами t GEV против Парето (2,5)

---

Статистические расстояния – это расстояния между распределениями или выборками, которые используются в различных приложениях машинного обучения, таких как обнаружение аномалий и выбросов, порядковая регрессия и генеративные состязательные сети (GAN). В этом посте рассказывается, как сравнивать распределения, используя как визуальные инструменты, так и надежные статистические расстояния.

При сравнении наборов данных статистические тесты могут сказать вам, могут ли две выборки данных быть сгенерированы одним и тем же процессом или же они каким-то образом связаны.Однако бывают случаи, когда вместо того, чтобы решать, отвергать ли статистическую гипотезу, вы хотите измерить, насколько схожи или далеки друг от друга наборы данных, без каких-либо предположений. Статистические расстояния, как расстояния между образцами, являются интересным ответом на эту проблему.

В этом посте мы рассмотрим:

Учитывая два разных набора данных, быстрого визуального осмотра часто бывает достаточно, чтобы сравнить их минимальные и максимальные значения, их средние значения и их разброс. Все это особенности их эмпирических распределений.

Например, эти два набора данных имеют одинаковый разброс, и оба сосредоточены вокруг нуля. Глядя на гистограммы их значений, создается впечатление, что они распределены одинаково.

Графики Q-Q – удобный инструмент для сравнения распределений. Давайте отсортируем каждый набор данных по значению, а затем сопоставим их друг с другом. Чем ближе значения к прямой линии (первая бисекторная линия), тем ближе они к аналогичному распределению. Точки здесь обозначают 25 ^-е , 50 ^-е и 75 ^-е процентили.

Учитывая, что их значения лежат близко к прямой линии, график Q-Q подтверждает то, что мы видели до сих пор.

Хотя визуальный осмотр является хорошей эвристикой, нам часто требуется количественная мера сходства между двумя распределениями. То есть нам нужно учитывать расстояние между распределениями.

Первое расстояние, которое мы рассматриваем, происходит от известного теста Колмогорова-Смирнова (КС). Чтобы сравнить два набора данных, мы строим их эмпирические кумулятивные функции распределения (CDF), сортируя каждый набор и рисуя нормализованную ступенчатую функцию, которая возрастает в каждой точке данных.Расстояние KS определяется как наибольшая абсолютная разница между двумя эмпирическими CDF, оцененными в любой момент.

В случае \ (A \) и \ (B \) максимальная разница составляет \ (0,07 \) (при \ (x = -1,0 \)):

Фактически, мы можем назвать это расстоянием , или метрика, потому что она удовлетворяет четырем условиям, которые формализуют интуитивное представление о расстоянии:

• его значение больше или равно нулю,
• оно равно нулю тогда и только тогда, когда оба распределения идентичны,
• он симметричен: расстояние от одного распределения до другого равно расстоянию от второго до первого,
• если \ (A \), \ (B \) и \ (C \) – распределения, то \ (\ KS (B, C) ≤ \ KS (B, A) + \ KS (A, C) \), или интуитивно, с определением \ (\ KS \), короче идти прямо от \ ( B \) в \ (C \), а не через \ (A \), что известно как неравенство треугольника.

Эти свойства делают дистанционную дистанцию ​​KS мощной и удобной в использовании. Следовательно, учитывая третий набор данных \ (C \):

У нас есть \ (\ KS (A, C) = 0,22 \):

Таким образом, мы можем сразу сделать вывод, что расстояние KS между \ (B \) и \ ( C \) не превосходит \ (0,29 \), поскольку \ (\ KS (B, C) ≤ \ KS (B, A) + \ KS (A, C) = 0,07 + 0,22 = 0,29 \).

Расстояние KS всегда находится между 0 и 1, поэтому его использование ограничено при сравнении распределений, которые далеко друг от друга. Например, если вы возьмете два нормальных распределения с одинаковым стандартным отклонением, но разными средними значениями, расстояние KS между ними не будет расти пропорционально расстоянию между их средними значениями:

Эта функция расстояния KS может быть полезна, если вас больше всего интересует насколько похожи ваши наборы данных, и как только становится ясно, что они разные, вас меньше заботит, насколько они разные.

Еще одно интересное статистическое расстояние – это расстояние земного движителя (EMD), также известное как первое расстояние Вассерштейна. Его формальное определение немного технически, но его физическая интерпретация, которая дает ему название, легко понять: представьте, что два набора данных представляют собой груды земли, а цель состоит в том, чтобы переместить первую кучу, чтобы она соответствовала второй. Расстояние землечерпалки – это минимальный объем работы, где «объем работы» – это количество земли, которое вы должны переместить, умноженное на расстояние, на которое вы должны ее переместить.Можно также показать, что EMD равна площади между двумя эмпирическими CDF.

EMD – хороший инструмент для дистрибутивов с длинными хвостами. Рассмотрим следующие наборы данных \ (D \), \ (E \) и \ (F \):

Мы вычисляем \ (\ EMD (D, E) = 0.12 \) и \ (\ EMD (D, F) = 1,76 \), т. Е. Примерно в 14 раз выше. Сравните это с \ (\ KS (D, E) = 0,08 \) и \ (\ KS (D, F) = 0,17 \), что всего в два раза выше. EMD подчеркивает тот факт, что хвост \ (F \) содержит значительный объем данных. Поскольку EMD неограничен, с ним может быть труднее работать, в отличие от расстояния KS, которое всегда находится между 0 и 1.

Мы можем рассматривать EMD как сумму абсолютной разницы между двумя эмпирическими CDF вдоль оси x. Расстояние Крамера-фон Мизеса (CM) получается путем суммирования квадратов разницы между двумя эмпирическими CDF вдоль оси x (а затем извлечения квадратного корня из суммы, чтобы сделать его действительным расстоянием). Связь между расстоянием CM и EMD аналогична соотношению норм L1 и L2.

Для предыдущего примера \ (\ CM (D, E) = 0,07 \) и \ (\ CM (D, F) = 0,32 \), что примерно в 4 раза больше.

Давайте снова рассмотрим пример двух нормальных распределений с разделенными средними. EMD линейно увеличивается по мере удаления средств друг от друга, тогда как расстояние KS быстро выравнивается. С другой стороны, расстояние CM растет как функция квадратного корня.

Обратите внимание, что расстояние KS – это максимум абсолютной разницы между CDF, тогда как EMD – это средняя абсолютная разница. Это свойство делает КС более чувствительным к локальным деформациям.Это также причина того, почему при сравнении выборки данных с теоретическим распределением тест KS требует большой выборки для точности.

В качестве примера рассмотрим два равномерных распределения \ (G \) и \ (H \), от 0 до 10, соответственно 1 и 11:

Вот их CDF:

Расстояния между \ (G \) и \ (H \):

• \ (\ KS (G, H) = 0,1 \),
• \ (\ EMD (G, H) = 1 \),
• \ (\ CM (G, H ) = 0,311 \).

Теперь давайте сгенерируем \ (I \) из \ (H \), введя локальную деформацию – мы накапливаем массу вокруг одной точки:

Вот CDF для \ (G \) и \ (I \) :

Расстояния между \ (G \) и \ (I \) и соответствующие увеличения от расстояний между \ (G \) и \ (H \) составляют:

• \ (\ KS (G, I) = 0.2 \), на 100% выше, чем \ (\ KS (G, H) \),
• \ (\ EMD (G, I) = 1.002 \), на 0,2% выше,
• \ (\ CM (G, I ) = 0,322 \), что на 3,6% больше.

Как видим, KS сильно подвержен деформации, тогда как EMD практически не изменяется. CM кажется здесь хорошим компромиссом, поскольку он все еще может обнаруживать деформацию, не будучи чрезмерно чувствительным.

Однако есть также деформации, которые не влияют на KS, а влияют только на EMD и CM. Рассмотрим следующие распределения \ (J \), \ (K \) и \ (L \):

Визуально, если вы возьмете \ (J \) в качестве ссылки, \ (L \) будет дальше, чем \ (K \).Высокие процентили для \ (K \) составляют около 3, а для \ (L \) – около 5. Следовательно, мы ожидаем, что расстояние между \ (J \) и \ (L \) будет больше, чем между \ ( J \) и \ (K \). Однако, если мы рассмотрим расстояние KS, мы получим:

• \ (\ KS (J, K) = 0,0495 \),
• \ (\ KS (J, L) = 0,0500 \).

Таким образом, относительная разница между расстояниями составляет всего около 1% (71% для EMD, 39% для CM). Мы могли сдвинуть небольшую бугорку дальше вправо, совершенно не влияя на расстояние KS.Чтобы понять, как это может происходить, давайте рассмотрим совокупные функции распределения \ (J \), \ (K \) и \ (L \):

Мы видим, что, сдвигая выступ, мы влияем на CDF \ (K \), которое становится \ (L \), но мы не влияем на максимальное вертикальное расстояние между кумулятивными функциями распределения, то есть расстояние KS.

Интерактивная визуализация в верхней части страницы позволяет выбрать два распределения и сгенерировать две случайные выборки из этих распределений (размером 2000).Затем вы можете визуализировать их график Q-Q и их CDF, а также значения расстояний Колмогорова-Смирнова, Двигателя Земли и Крамера-фон Мизеса между обоими образцами.

У всех обсуждаемых здесь методов есть свое место. Существует множество инструментов построения графиков для проведения визуальных проверок, и расстояние KS широко реализовано (для Python в Scipy есть реализация KS). В июле мы представили реализацию и расстояния Earth Mover (также известного как первое расстояние Вассерштейна) и энергетического расстояния (которое тесно связано с расстоянием Крамера-фон Мизеса) в качестве запроса на включение для включения в SciPy.PR был недавно объединен, и наши реализации будут доступны в следующей версии SciPy (а именно версии 1.0).

---

• Расстояние земного движителя хорошо обобщается на несколько измерений, но требует первично-двойного алгоритма для вычисления расстояния. Двумерный случай часто используется при обработке изображений.
• На самом деле существует две версии расстояния Крамера-фон Мизеса:
  • оригинальная версия без распространения, представленная Крамером в 1928 году, которая рассматривается здесь,
  • версия без распространения, представленная Смирнова в 1936 г., который используется, например, в критерии Крамера-фон Мизеса.
• Версия расстояния Крамера-фон Мизеса, не связанная с распространением, тесно связана с энергетическим расстоянием, так как его квадрат равен \ (2 \ E‖XY‖ – \ E‖X – X’‖ – \ E ‖Y – Y’‖ \), где \ (X \), \ (X ‘\) – независимые случайные величины, распределенные согласно одному распределению, а \ (Y \), \ (Y’ \) – irv распределяется согласно другому. Тем, кто знаком с анализом Фурье, следует вспомнить теорему Планшереля. Однако вычислить расстояние от CDF намного быстрее.
• У Крамера-фон Мизеса есть взвешенная версия под названием Андерсон-Дарлинг, которая используется в качестве теста для определения, являются ли два распределения одинаковыми или нет. Однако это не расстояние, и его значение очень чувствительно к размеру выборки.
• Здесь мы рассматриваем только одномерные распределения, но если размерность вашего набора данных выше, и вам нужно только знать, находятся ли ваши два набора данных близко или далеко друг от друга, тестирование свойств становится интересным. Клеман Канонн написал хороший технический обзор (и сопутствующий блог) о тестировании дистрибутивов.

Как измерять расстояния в машинном обучении | Юге Изаугарат

Все зависит от точки зрения

«Если вы выкопаете яму здесь, в Германии, вы окажетесь в Китае» – Я так сильно рассмеялся, когда мои европейские друзья сказали мне это.

Не потому, что я думал, что это абсурд или что-то в этом роде. Но потому что это высказывание было очень распространено и в Аргентине. Я не думал, что это всемирная поговорка.

«Правда? это тоже распространено там? » – Они были удивлены не меньше меня.

«Подождите! Есть веб-сайт, на котором вы можете узнать, где вы окажетесь, если выкопаете яму там, где стоите »- Сказал мой друг. У него всегда был свой сайт для всего.

«Как вы думаете, почему здесь и там одно и то же?» – Другой друг спросил – «Возможно, потому что это указывает на место, которое находится далеко от того места, где мы родились»

«Для меня Испания очень далеко» – Кто-то другой заявил

От меня, моя родная страна было далеко.Так что для меня 13000 км было далеко. Для некоторых моих друзей 2000 км были очень далеко.

Я начал думать о том, насколько сложным было понятие расстояния, если посмотреть на него субъективно.

Иногда вы сидите напротив кого-то, но этот человек кажется таким далеким. В других случаях человек находится за несколько километров. И сообщение – это все, что нужно, чтобы почувствовать, что кто-то очень близок.

В некоторых случаях я предполагаю, что близкое и далекое зависит от точки зрения.

В машинном обучении многие контролируемые и неконтролируемые алгоритмы используют метрики расстояния для понимания закономерностей во входных данных.Кроме того, он используется для распознавания сходства между данными.

Выбор хорошей метрики расстояния повысит эффективность алгоритмов классификации или кластеризации.

A Distance Metric использует функции расстояния, которые говорят нам расстояние между элементами в наборе данных.

К счастью, эти расстояния можно измерить с помощью математической формулы. Если расстояние небольшое, скорее всего, элементы похожи. Если расстояние большое, степень сходства будет низкой.

Можно использовать несколько показателей расстояния. Важно знать, что они принимают во внимание. Это поможет нам выбрать, какая из них больше подходит для модели, чтобы избежать ошибок или неверных интерпретаций.

1 Евклидово расстояние: Когда мы говорили о расстояниях ранее, мы в основном думаем о расстояниях по более или менее прямой линии.

Если мы думаем о расстоянии между двумя городами, мы думаем о том, сколько километров нам нужно проехать по шоссе.

Эти примеры расстояний, которые мы можем придумать, являются примерами евклидова расстояния . По сути, он измеряет длину сегмента, соединяющего две точки. Давайте посмотрим на график:

Евклидово расстояние

Звонит ли это в колокол? Вы помните теорему Пифагора из математических классов?

Теорема утверждает, что квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон .

Ну, с его помощью можно рассчитать евклидово расстояние.

В нашем примере у нас есть расстояние между двумерными точками, поэтому формула:

Для n точек общая формула выглядит следующим образом:

Где x и y – два вектора.

Евклидово расстояние – это наиболее часто используемое расстояние для алгоритмов машинного обучения. Это очень полезно, когда наши данные непрерывны. Его также называют L2-Norm .

Итак, недостаточно евклидова расстояния? Зачем нужен другой тип расстояний?

Бывают ситуации, когда евклидово расстояние не дает нам правильной метрики.В этих случаях нам нужно будет использовать разные функции расстояния.

2 Манхэттенское расстояние: Допустим, мы снова хотим вычислить расстояние между двумя точками. Но на этот раз мы хотим сделать это в виде сетки, как фиолетовая линия на рисунке.

В данном случае соответствующая метрика – Манхэттенское расстояние. Определяется как сумма абсолютных разностей их декартовых координат.

Поясним это. Точка данных имеет набор числовых декартовых координат, которые однозначно определяют эту точку.

Эти координаты представляют собой расстояние со знаком от точки до двух фиксированных перпендикулярных ориентированных линий, таких как линия, показанная на рисунке ниже. Это также может вызвать некоторые воспоминания на уроках математики, верно?

Декартова система координат

Итак, в нашем примере манхэттенское расстояние будет вычисляться следующим образом: Получите разность (Δx = x2-x1) и разность по оси y (Δy = y2-y1). Затем получите их абсолютное число | Δx | и, наконец, просуммируйте оба значения.

В общем случае формула имеет следующий вид:

Манхэттенская метрика расстояния также называется расстоянием L1 или нормой L1.Если вы знакомы с регуляризацией машинного обучения, вы, вероятно, слышали это раньше.

Рекомендуется использовать его при работе с данными большой размерности. Кроме того, если вы вычисляете ошибки, это полезно, когда вы хотите акцентировать внимание на выбросах из-за их линейного характера.

3 Расстояние Минковского: Прежде всего, мы определим некоторые математические термины, чтобы впоследствии определить расстояние Минковского .

• Векторное пространство – это набор объектов, называемых векторами, которые можно складывать вместе и умножать на числа (также называемые скалярами ).
• Норма – это функция, которая назначает строго положительную длину каждому вектору в векторном пространстве (единственное исключение – нулевой вектор, длина которого равна нулю). Обычно обозначается как ∥x∥.
• A Нормированное векторное пространство – это векторное пространство над действительными или комплексными числами, на котором определена норма.

При чем здесь расстояние Минковского?

Расстояние Минковского определяется как метрика подобия между двумя точками в нормированном векторном пространстве (N-мерное реальное пространство).

Он также представляет собой обобщенную метрику, которая включает евклидово и манхэттенское расстояние.

Как выглядит формула?

Если мы обратим внимание, когда λ = 1, у нас есть манхэттенское расстояние. Если λ = 2, мы находимся на евклидовом расстоянии. Существует еще одно расстояние, называемое расстоянием Чебышева , которое возникает при λ = ∞.

В целом, мы можем изменить значение λ для вычисления расстояния между двумя точками разными способами.

Когда мы его используем? Расстояние Минковского часто используется, когда интересующие переменные измеряются на шкале отношений с абсолютным нулевым значением.

4 Махаланобис Расстояние: Когда нам нужно вычислить расстояние между двумя точками в многомерном пространстве, нам нужно использовать расстояние Махаланобиса.

Мы уже говорили о декартовой системе координат. Провели перпендикулярные линии. Затем мы рассчитали расстояния в соответствии с этой системой осей.

Это очень легко сделать, если наши переменные не коррелированы. Потому что расстояния можно измерить прямой линией.

Допустим, присутствуют две или более коррелированных переменных.Также добавим, что мы работаем с более чем 3 измерениями. Теперь проблема усложняется.

В таких случаях нас спасает расстояние Махаланобиса. Он измеряет расстояние относительно центроида для многомерных данных. В этой точке пересекаются средние от всех переменных.

Его формула следующая:

, где Xa и Xb – пара объектов, а C – выборочная ковариационная матрица.

5 Косинусное сходство: Представим, что вам нужно определить, насколько похожи два документа или корпус текста.Какие показатели расстояния вы будете использовать?

Ответ: косинусное сходство .

Чтобы вычислить его, нам нужно измерить косинус угла между двумя векторами. Затем косинусное сходство возвращает их нормализованное скалярное произведение.

Нормализованный вектор – это вектор в том же направлении, но с нормой 1.

Скалярное произведение – это операция, в которой два вектора одинаковой длины умножаются, в результате получается один скаляр.

Косинусное подобие

Итак, формула косинусного подобия:

где A и B – векторы, ∥ A∥ и ∥ B∥ – норма A и B, а cosθ – косинус угла между A и B. .Это также можно записать в других терминах:

Косинусное сходство очень полезно, когда нас интересует ориентация, а не величина векторов.

Два вектора с одинаковой ориентацией имеют косинусное сходство, равное 1. Два вектора под углом 90 ° имеют сходство, равное 0. Два диаметрально противоположных вектора имеют сходство, равное -1. Все независимо от их величины.

6 Расстояние Жаккара: Наконец, мы изменим фокус нашего внимания. Вместо вычисления расстояний между векторами мы будем работать с множествами.

Набор – это неупорядоченный набор объектов. Так, например, {1, 2, 3, 4} равно {2, 4, 3, 1}. Мы можем вычислить его количество элементов (представленное как | set |), которое является не чем иным, как количеством элементов, содержащихся в наборе.

Допустим, у нас есть два набора объектов, A и B. Нам интересно, сколько элементов у них общего. Это перекресток . Математически он представлен как A ∩ B.

Возможно, мы хотим получить все элементы, независимо от того, к какому набору они принадлежат.Он называется Union . Математически он представлен как A ∪ B.

Мы можем лучше представить это, используя диаграммы Венна.

Пересечение и Союз представлены голубым цветом на диаграммах Венна.

Как это связано со сходством Жаккара? Подобие Жаккара определяется как мощность пересечения определенных множеств, деленная на мощность их объединения.