Одна из самых экстремальных фигур на плоскости: треугольник Рёло
Randomguy
Автор:
Randomguy
06 февраля 2022 11:48
Метки: геометрия интересное математика наука ученые факты
30524
5
2
Что это вообще такое? Квадратный круг? Круглый квадрат? История этого треугольника длится уже сотни лет.
Источник:
Чтобы построить треугольник Рёло понадобится циркуль. Установили, провели окружность. Потом нужно поставить циркуль на любую точку и проводите еще одну окружность. Затем ставите циркуль на одну из точек пересечения окружностей и проводите третью.
Источник:
Главное свойство треугольника Рёло – это фигура постоянной ширины, наряду, к примеру, с окружностью. Нужно знать понятие опорных прямых, чтобы понять, что такое постоянная ширина.
Опорная прямая – это та прямая, что содержит точку фигуры, но не разделяющая никакие две точки на ней. На рисунке выше проведены три пары опорных прямых, расстояние между которыми равно постоянной ширине треугольника Рёло.
Треугольник Рёло имеет минимальную площадь из всех фигур постоянной ширины, а окружность максимальную.
А есть еще другое экстремальное свойство треугольника Рёло: все его углы при вершинах так же минимальны среди всех фигур с постоянной шириной:
А есть еще такие треугольники и с большим количеством углов.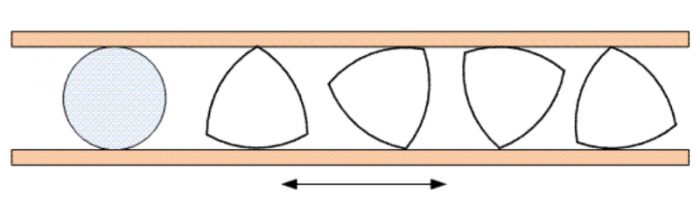 Проходя через точку а все опорные прямые, которых бесконечность, образуют т.н. пучок, угол между крайними положениями которого равен углу при вершине треугольника Рёло – 120 градусов. И меньше на плоскости быть никак не может.
Проходя через точку а все опорные прямые, которых бесконечность, образуют т.н. пучок, угол между крайними положениями которого равен углу при вершине треугольника Рёло – 120 градусов. И меньше на плоскости быть никак не может.Но вот какое самое поражающее свойство треугольника Рёло – это то, что он может вписаться в квадрат с равной стороной!
Источник:
Треугольник Рёло почти полностью повторяет контур квадрата и это позволяет на его основе делать, к примеру, сверла, которые вырезают близкие к квадратам отверстия.
“Круглое тащим, квадратное катаем” – этот очень распространенный армейский принцип точно не подойдет к треугольнику Рёло. Даже несмотря на углы, колеса такой формы даже на небольших скоростях заменят обычные круглые.
2022-02-06T11:48:16+03:00
youtube.com/embed/_o8XhfJCGW8?hl=ru_RU&wmode=transparent&fs=1″ wmode=”transparent” webkitallowfullscreen=”” mozallowfullscreen=”” allowfullscreen=””>“Круглое тащим, квадратное катаем” – этот очень распространенный армейский принцип точно не подойдет к треугольнику Рёло. Даже несмотря на углы, колеса такой формы даже на небольших скоростях заменят обычные круглые.
Ну и кроме всего этого треугольник Рёло используется в кулачковых механизмах паровых двигателей, так как может преобразовывать вращательное движение в возвратно-поступательное.
2022-02-06T11:48:16+03:00
Ну и кроме всего этого треугольник Рёло используется в кулачковых механизмах паровых двигателей, так как может преобразовывать вращательное движение в возвратно-поступательное.
В специальном роторном двигателе Венкеля треугольник позволяет выполнить сразу три цикла сгорания топлива в один такт.
Источник:
Источник:
Ссылки по теме:
- Что самое противное на вкус
- Ученые рассказали о целебных свойствах музыки для мозга
- Амбициозные проекты СССР, которые так и не реализовали
- Конец Николы Теслы: последняя фотография изобретателя
- Тихоходка: что это за жуть рядом с нами и как ее убить
Метки: геометрия интересное математика наука ученые факты
Новости партнёров
реклама
| Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №1 Камышловского городского округа.  Тема проекта Феномен круглого треугольника Исполнители: Михайлов Алексей Камышлов, 2015 Оглавление Введение……………………………………………………………………………………………..3 Глава 1. История изобретения треугольника Рело………………………….4 1.1.Понятие треугольника Рело………………………………………………………….4 1.2.История изобретения треугольника Рело…………………………………….5 Глава 2. Основные характеристики и свойства треугольника Рело..7 2.1. Способы построения треугольника Рело …………………………………..7 2.2. Геометрические характеристики и свойства треугольника Рело..7 Глава 3. Применение треугольника Рело………………………………………10 Заключение …………………………………………………………………………………..…..15 Литература………………………………………………………………………………………….16 Приложение ………………………………………………………………………………………17 Введение «Изобретением велосипеда» называют бессмысленное повторение и переоткрытие давно пройденного и известного, и совершенно напрасно. Цель работы — формирование представления о феномене круглого треугольника Достижение поставленной цели предполагает решение следующих задач: · проанализировать различные источники информации по проблеме феномена круглого треугольника · Рассмотреть и изучить геометрические свойства треугольника Рело; · Выяснить области применения треугольника Рело. · Найти объяснение плавности хода модели с «треугольными колесами» Объект исследования: треугольник Рело, как технический феномен. Предмет исследования: основные свойства треугольника Рело. Методы исследования. Для решения поставленных задач использованы: анализ литературы по теме, сбор и систематизация материалов, анализ и интерпретация полученных данных, эмпирические метод. Гипотеза: Треугольнику Рело присущи свойства обеих геометрических фигур, используемых в его построении, кроме того он обладает собственными свойствами, которые используются в технике. Глава 1. История изобретения треугольника Рело 1.1.Понятие треугольника Рело. Рассмотрим правильный треугольник (с равными сторонами). На каждой стороне построим дугу окружности, радиусом, равным длине стороны. Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Треугольник Рёло является простейшей после круга фигурой постоянной ширины. То есть если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной треугольника Рёло. 1.2.История изобретения треугольника Рело. Название фигуры происходит от фамилии немецкого механика Франца Рёло (1829 – 1905). Он, вероятно, был первым, кто исследовал свойства этого треугольника; также он использовал его в своих механизмах. Изучая историю происхождения треугольника Рело, мы выяснили, что Рело не является первооткрывателем этой фигуры. Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов. (Приложение 1 рис.2) Глава 2. Основные характеристики и свойства треугольника Рело. 2.1. Различные способы построения треугольника Рело. Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. На каждой стороне равностороннего треугольника построим дугу окружности с центром в третьей вершине треугольника. Получим треугольник Рёло. Его ширина во всех направлениях одинакова. (Ширина фигуры в данном направлении — это расстояние между её опорными параллельными этому направлению прямыми, то есть параллельными прямыми, между которыми заключена фигура и расстояние между которыми нельзя уменьшить с сохранением этого свойства.) 2.2. Геометрические характеристики и свойства треугольника Рело Треугольник Рело обладает следующими геометрическими характеристиками:
Таким образом первоначально выдвинутая гипотеза о том, что треугольник Рело будет сочетать в себе свойства круга и равностороннего треугольника, а также характеризуется только ему присущими свойствами, подтверждена в ходе исследования. . Глава 3. Применение треугольника Рело Применение треугольника Рело основано на его свойствах. Основные сферы применения в технике: сверло Уаттса (сверление квадратных отверстий), роторно-поршневой двигатель Ванкеля (внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень – треугольник Рело), грейферный механизм в кинопроекторах (используется свойство вращения треугольника Рело в квадрате со стороной ), кулачковые механизмы паровых двигателей, швейных машин и часовых механизмов, катки для транспортировки тяжелых грузов, крышки для люков (свойство постоянной ширины), в качестве медиатора. Кроме того, еще с XIII века используется свойство симметричности и гармонии в архитектурных сооружениях на основе стрельчатых арок и элементов орнамента. Рассмотрим по подробнее, применение треугольника Рело, в некоторых механических устройствах. В 1914 году английский инженер Гарри Джеймс Уаттс изобрёл инструмент для сверления квадратных отверстий (Приложение 6 рис.7), с 1916 года сверла находятся в серийном производстве. Сверло Уаттса представляет собой треугольник Рело, в котором заточены ржущие кромки и прорезаны углубления для отвода стружки. Замечено что вершины треугольника Рёло описывают квадрат только при вращение центра строго по фигуре состоящей из 4 дуг эллипсов. Отсюда и сложность создания такого сверла, так как обычная дрель вращает сверло вокруг своей оси. Треугольник Рело используется и в автомобильных двигателях (Приложение 7 рис.8). В 1957 году немецкий инженер, изобретатель Ф. Ванкель, сконструировал роторно-поршневой двигатель. Внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень – треугольник Рело. Он вращается так, что три его вершины находятся в постоянном контакте с внутренней стенкой корпуса, образуя три замкнутых объёма, или камеры сгорания. Фактически каждая из трёх боковых поверхностей ротора действует как поршень. При всех достоинствах РПД – компактности, приемистости, отсутствии кривошипно-шатунного и газораспределительного механизмов, а так же значительно меньших габаритов и массе при одинаковой с поршневыми двигателями внутреннего сгорания мощности, он имеет и ряд серьезных недостатков: часто выходящие из строя уплотнительные элементы, плохая приспосабливаемость к изменениям внешней нагрузки, повышенный расход топлива и неудовлетворительные показатели по выбросам в отработавших газах.Тем не менне в серийном производстве находятся автомобили Mazda RX-8. Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. Впрочем, по прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. В кинематографии используется — «Грейферный» механизм (Приложение 8 рис.9), который осуществляет покадровое перемещение плёнки в кинопроекторах. Устройство грейферного механизма основано на треугольнике Рело, вписанном в квадрат и двойном параллелограмме, который не дает квадрату наклоняться в стороны. Действительно, т.к. длины противоположных сторон равны, то среднее звено при всех движениях остается параллельным основанию, а сторона квадрата всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера. Такой механизм обеспечивает равномерное вращение оси, чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду. В форме треугольника Рёло можно изготавливать крышки для люков — опытным путем доказано, что благодаря постоянной ширине они не могут провалиться в люк. Возможно применение треугольника Рёло и в мотоиндустрии. Всем известно, для того, чтобы приводить мотоцикл в движение необходимо «крутить ручку газа». В мотоиндустрии проблема с хорошим хватом этой ручки стоит остро. Её решали по-разному, к примеру: используя материалы, повышающие трение между перчаткой и ручкой газа. К тому же, при длительной езде рука попросту устает. Ради решения этой проблемы, специалисты, экспериментально, изготовили из дерева ручку, которая при фронтальном разрезе имела форму треугольника Рёло и, как оказалось, она идеально повторяет внутренние контуры закрытой ладони, и удерживать такую рукоять гораздо легче. Как оказалось, при простейшем изучении вашей ладони вы увидите, что если собрать руку «трубочкой», как будто вы держите что-нибудь круглое, то вторая и третья фаланга второго, третьего и четвертого, а также вторая фаланга первого пальца (замыкающего «кольцо» из вашей ладони) образуют вершины круглого треугольника, что полностью доказывает удобство такой ручки. Данное открытие можно использовать не только для ручек мотоцикла, но и везде где необходимо удерживать с сопротивлением поворотную рукоять такого типа. Форма треугольника Рёло, его свойство симметричности, используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло использовали еще в VIII векев церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде. Как элемент орнамента он встречается на оконных решётках цистерцианского аббатства в швейцарской коммуне Отрив (Приложение 9 рис. Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру. В научно-фантастическом рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало колёса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло. Заключение Изучив литературу, просмотрев видео материалы, рассмотрев большое количество областей, где только возможно применение треугольника Рёло, мы получили интересный результат. А заключается он в том, что применение данного треугольника в окружающем нас мире, может быть гораздо большем, чем мы могли бы подумать. Мы считаем, что нельзя так беззаботно обходить треугольник Рёло, его можно использовать в различных механизмах. В своей работе мы не только изучили его свойства, геометрические характеристики, историю изобретения, но и рассмотрели сферы применения этой выпуклой, симметричной фигуры постоянной ширины. Выдвинутая нами гипотеза о свойствах этой фигуры нашла свое подтверждение. Кроме того, мы ответили для себя на ряд вопросов познавательного характера: какие геометрические свойства обеспечивают плавность хода велосипеда с «треугольными» колесами, почему канализационные люки делают круглыми или в форме треугольника Рело. Не менее познавательной оказалась информация о сферах применения «круглого» треугольника не только в технике, но и в архитектуре, литературе. Таким образом, поставленные нами задачи, реализованы в полном объеме Литература
Сайты в Интернете:
Приложение 1 Рис.1 Рис.2 Приложение 2 Рис.3 Приложение 3 Рис.4 Приложение 4
Приложение 5 рис.6 Приложение 6 Рис.7
Приложение 8 Приложение 9 рис.10 |
Круговой треугольник Рело / Этюды // Математические этюды
Круговой треугольник Рело / Этюды // Математические этюдыМатематические этюды
Вернуться к списку
Вот и “Луч-2”, восьмимиллиметровый кинопроектор. Он был в каждом русском доме, где кинолюбители снимали и смотрели фильмы.
Он был в каждом русском доме, где кинолюбители снимали и смотрели фильмы.
В этой карикатуре представлено геометрическое понятие, часто изучаемое в математических кружках, и его применение в нашей повседневной жизни.
Колесо… Круг. Одним из свойств круга является его постоянная ширина. Нарисуем две параллельные линии и зафиксируем расстояние между ними. Давайте начнем их вращать. Кривая (в данном случае круг) постоянно касается обеих линий. Это определение того, что замкнутая кривая имеет постоянную ширину.
Существуют ли кривые, отличные от окружностей постоянной ширины?
Рело, Франц 1829—1905
Французский ученый. Был первым (1875 г.) правильно сформулировал основные вопросы строения и кинематики механизмов; разрабатывал проблемы проектирования технических механизмов.
Рассмотрим правильный треугольник. На каждой стороне треугольника начертим дугу окружности радиусом, равным длине стороны. Эта кривая называется треугольником Рело.
В бытовом смысле постоянная ширина кривой означает, что если сделать колеса с таким профилем, то книга будет катиться по ним, не шевелясь.
Однако сделать колесо с таким профилем невозможно, так как центр этой фигуры описывает сложную линию при качении.
Существуют ли другие кривые постоянной ширины? Оказывается, их бесконечно много.
На любом правильном многоугольнике с нечетным числом вершин можно построить кривую постоянной ширины по схеме построенного треугольника Рело. Необходимо провести дугу окружности, соединяющую концы противоположной стороны и центра в каждой вершине.
Рассматриваемые кривые не исчерпывают весь класс кривых постоянной ширины. Оказывается, существуют несимметричные кривые постоянной ширины. Мы рассматриваем произвольный набор пересекающихся прямых. Затем рассматриваем один из секторов. Проведем дугу окружности с центром в точке пересечения линий, определяющих этот сектор, и случайным радиусом. Затем рассмотрим следующий сектор и проведем окружность с центром в точке пересечения линий, ограничивающих этот сектор. Радиус выбирается так, чтобы часть уже нарисованной кривой можно было непрерывно удлинять. Продолжим наше построение дальше. Получается, что кривая замкнется и мы получим кривую постоянной ширины. Докажи это
Все кривые заданной ширины имеют равные периметры. Окружность и треугольник Рело выделяются из всех остальных кривых заданной ширины своими экстремальными свойствами. Окружность ограничивает наибольшую площадь, а треугольник Рело — наименьшую.
Треугольник Рело часто изучают в математических кружках. Оказывается, у этой геометрической фигуры есть интересные приложения в механике.
Смотри, это Mazda RX-7. В отличие от большинства серийных автомобилей он (а также модель RX-8) оснащен роторным двигателем Ванкеля. Как это устроено? В качестве ротора используется треугольник Рело! Ротор разделяет камеру на три части, каждая из которых по очереди становится камерой сгорания. Сначала впрыскивается топливно-воздушная смесь синего цвета, затем за счет движения ротора она сжимается, воспламеняется и закручивает ротор. Роторный двигатель лишен некоторых недостатков свободнопоршневого двигателя. Например, здесь вращение передается непосредственно на ось и не обязательно использовать коленчатый вал.
А это когтевой механизм. Он использовался в кинопроекторах. Двигатели дают равномерное вращение оси. Но для резкого изображения необходимо тянуть пленку на один кадр, останавливать, а потом снова быстро тянуть. И так 18 раз в секунду.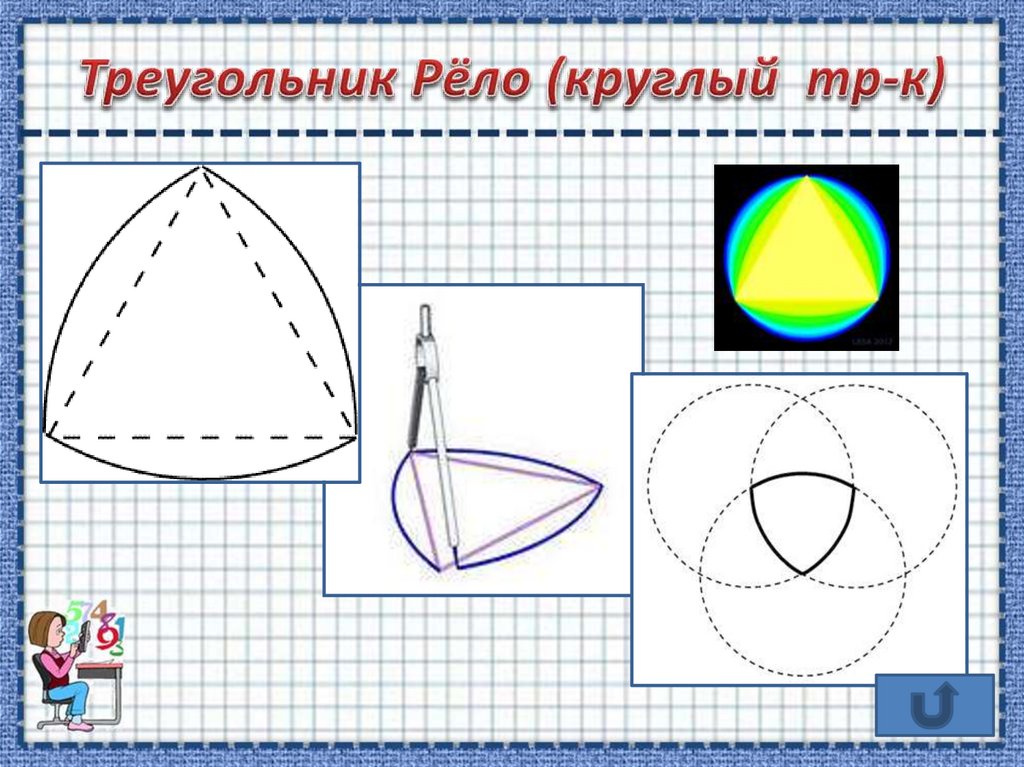 Коготь-механизм решает эту проблему. В его основе треугольник Рело, вписанный в квадрат, и два параллелограмма, препятствующие его отклонениям. Действительно, так как длины противоположных сторон равны, то среднее сечение, основание и сторона квадрата всегда параллельны друг другу. Чем ближе ось зажима к вершине треугольника Рело, тем ближе фигура, описываемая зубочелюстным аппаратом, к квадрату.
Коготь-механизм решает эту проблему. В его основе треугольник Рело, вписанный в квадрат, и два параллелограмма, препятствующие его отклонениям. Действительно, так как длины противоположных сторон равны, то среднее сечение, основание и сторона квадрата всегда параллельны друг другу. Чем ближе ось зажима к вершине треугольника Рело, тем ближе фигура, описываемая зубочелюстным аппаратом, к квадрату.
Можно было бы подумать, что чисто математические задачи находят интересные приложения.
Другие этюды из раздела «Кривые постоянной ширины»
Сверление квадратных отверстий Изобретение колесаМатематические этюды
С Днем Пи! – Мост для входа в высшую математику
С 𝝅 Днём! Мы празднуем с многоугольниками Рело и замечательным свойством, которое связывает их с 𝝅. Мы также рассмотрим некоторые из многих приложений этих интересных форм, коснемся некоторых важных математических результатов и даже зададим несколько открытых вопросов в мире многоугольников Рело!
Многоугольники Рело и 𝝅
Треугольник Рело — это «кривая постоянной ширины». Это просто означает, что всякий раз, когда вы обнимаете их двумя параллельными линиями, они всегда находятся на одинаковой ширине друг от друга:
Это просто означает, что всякий раз, когда вы обнимаете их двумя параллельными линиями, они всегда находятся на одинаковой ширине друг от друга:
Из-за этого вы можете использовать их как колеса или во множестве других мест, где вы могли бы «обычно» использовать круг (или где круги не годятся, например, сверло, которое делает квадратные отверстия). Подробнее об этом ниже!
Вы можете построить треугольник Рело, взяв три пересекающихся круглых диска, каждый с центром на границе двух других, например:
В качестве альтернативы вы можете представить его как равносторонний треугольник, в котором каждая сторона треугольника заменена дугой окружности, центр которой находится в противоположной вершине.
Но дело не только в треугольниках! Существует бесконечно много многоугольников Рело, которые мы можем построить аналогичным образом. Начните с любого правильного многоугольника с нечетным числом сторон, замените каждое ребро дугой окружности, центр которой находится на противоположной вершине, и вуаля — у вас есть еще один полигон Рело!
Начните с любого правильного многоугольника с нечетным числом сторон, замените каждое ребро дугой окружности, центр которой находится на противоположной вершине, и вуаля — у вас есть еще один полигон Рело!
Так что насчет соединения с 𝝅 ? Ну, это не слишком отличается от круга. Вы наверняка знаете формулу нахождения длины окружности:
с = πd
Разделите на d , чтобы получить c / d = π . Это дает нам фундаментальное свойство кругов: когда вы делите длину окружности на диаметр, вы всегда получаете π независимо от размера круга.
Для треугольника Рело мы ссылаемся на периметр p вместо длины окружности и говорим на ширину w вместо диаметра. (Это всего лишь разные названия одних и тех же понятий.) Чтобы найти периметр, заметьте, что угол при вершине равностороннего треугольника равен 60 градусам. Тогда дуга на противоположной стороне треугольника составляет 1/6 пути вокруг окружности с радиусом w . Потому что вся окружность будет 2wπ , это означает, что длина этой дуги:
Тогда дуга на противоположной стороне треугольника составляет 1/6 пути вокруг окружности с радиусом w . Потому что вся окружность будет 2wπ , это означает, что длина этой дуги:
2wπ / 6 = ( π / 3 )w
Сложите все три дуги, образующие треугольник Реле, и вы получите πw для его периметра.
Разделим на ширину и получим:
p / w = πw / w = π
Это означает, что, как ни удивительно, треугольники Рело имеют те же отношения с π, что и у круга! Фактически, тот же расчет работает, если мы начнем с ЛЮБОГО правильного n -угольника, где n нечетно, поэтому на самом деле это соотношение справедливо для ВСЕХ полигонов Рело. (Читайте дальше, чтобы узнать о еще большем обобщении этого результата.)
(Читайте дальше, чтобы узнать о еще большем обобщении этого результата.)
Приложения
Тот факт, что многоугольники Рело представляют собой кривые постоянной ширины, делает их популярными для использования в различных условиях. Поскольку они прекрасно катятся, монет , имеющих форму многоугольника Рело, все еще можно использовать в торговых автоматах! Некоторые примеры включают канадский луни (11-угольник Рело) и монету в 2 пулы из Ботсваны (7-угольник Рело).
Как и в случае широко используемых круглых крышек люков , постоянная ширина многоугольников Рело означает, что с небольшим краем внизу они не могут попасть в отверстия, для закрытия которых предназначены.
Фото Оуэна Бирна
Так почему же их обычно не используют в качестве крышек люков? Ну, а если вам нужно перекатить их на бок, то из-за центра тяжести их перекатывать труднее… Но именно это свойство делает их желательными для изготовления карандаши с поперечным сечением Рело. Они с меньшей вероятностью упадут с вашего стола.
Они с меньшей вероятностью упадут с вашего стола.
Точно так же клапан пожарного гидранта в форме треугольника Рело может помочь предотвратить вред, так как вам понадобится специальный инструмент, чтобы открыть его.
Найдите головку болта с треугольником Рело?
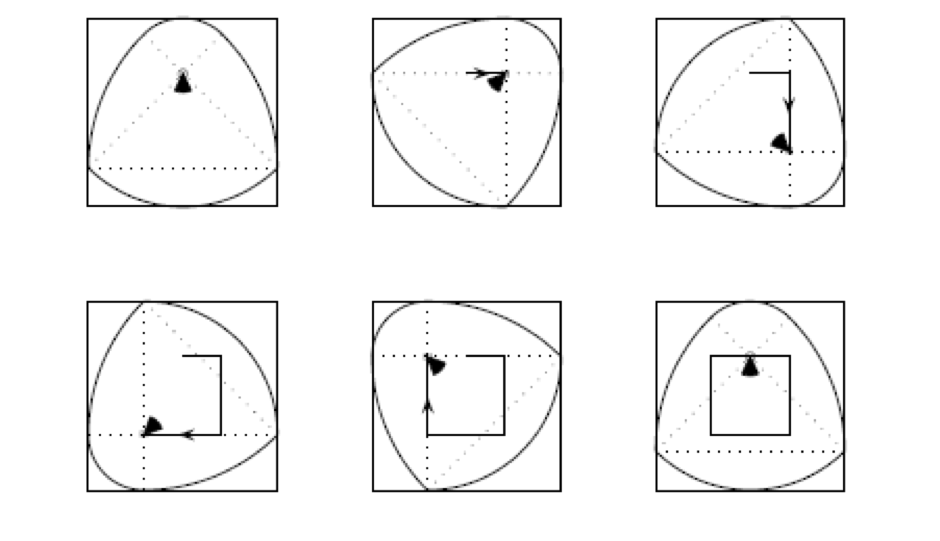
Треугольники Рело также имеют очень классное отношение к квадратам! Они могут образовывать ротор внутри квадрата, то есть делают полный оборот внутри квадрата, сохраняя контакт со всеми четырьмя сторонами.
В начале 1900-х компания Watt’s Brothers Tool Works использовала эту связь, чтобы запатентовать сверло , которое может сверлить квадратные отверстия! Вы можете просмотреть оригинальный патент!
И если вам интересно, откуда эти формы получили свое название, то оно принадлежит Францу Рёло (1829–1905), немецкому инженеру-механику, изучавшему и проектировавшему механизмы, преобразующие вращение вокруг фиксированной оси в возвратно-поступательное или движение вверх-вниз.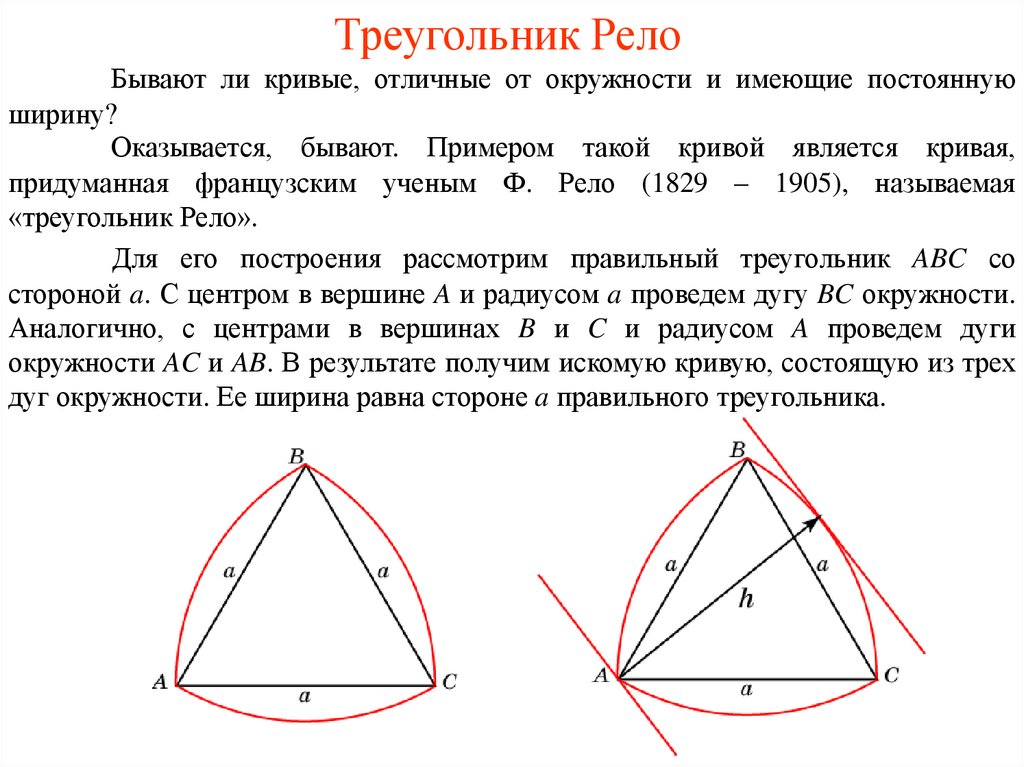 Одним из возможных применений является механизм подачи пленки 9.0130 , как здесь:
Одним из возможных применений является механизм подачи пленки 9.0130 , как здесь:
Большие математические результаты и открытые вопросы
Теорема Барбье , впервые опубликованная в 1860 году, показала, что каждая кривая постоянной ширины имеет такое же отношение к тому, что мы празднуем сегодня, а именно p / w = п .
Интересуетесь площадью треугольника Рело? Известно, что это 1 / 2 (π-√3)w 2 . Если вы хотите попытаться вывести его самостоятельно, вы можете рассмотреть возможность разбиения его на внутренний равносторонний треугольник и три криволинейные области, образованные между этим треугольником и дугами окружности.
Теорема Бляшке-Лебега доказывает, что треугольник Рело имеет наименьшую площадь всех кривых фиксированной постоянной ширины.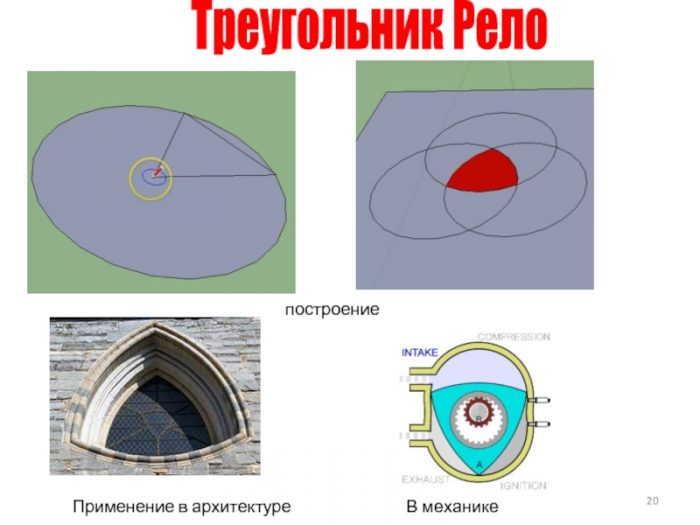

 Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. И вот в 2009 году китайский офицер Гуан Байхуа из Циндао заново изобрел колесо. Он создал необычный велосипед: вместо круглых колес у него треугольник сзади и пятиугольник спереди. Сам изобретатель уверен, что новая модель будет пользоваться популярностью, поскольку, чтобы передвигаться на таком велосипеде, требуется больше усилий, а значит, это в какой-то степени может заменить спортивную нагрузку.
Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. И вот в 2009 году китайский офицер Гуан Байхуа из Циндао заново изобрел колесо. Он создал необычный велосипед: вместо круглых колес у него треугольник сзади и пятиугольник спереди. Сам изобретатель уверен, что новая модель будет пользоваться популярностью, поскольку, чтобы передвигаться на таком велосипеде, требуется больше усилий, а значит, это в какой-то степени может заменить спортивную нагрузку. 
 Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.
Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло. В 1852 он окончил политехникум в Карлсруэ, с 1856 профессор Политехнического института в Цюрихе, в 1864—1896 профессор Промышленного института (позже — Высшая техническая школа) в Берлине. В 1875 впервые четко сформулировал и изложил основные вопросы структуры и кинематики механизмов, которые ранее содержались в неявной форме в работах П. Л. Чебышева и др. Рело дал определение кинематической пары, кинематической цепи и механизма как кинематической цепи принуждённого движения; предложил способ преобразования механизмов путём изменения стойки и путём изменения конструкций кинематических пар. Связал теорию механизмов и машин с проблемами конструирования, например, впервые поставил и пытался решить проблему эстетичности технических объектов. Имея в виду это направление его работ, современники Рело называли его поэтом в технике. Творчество Рело оказало значительное влияние на последующие исследования по теории механизмов.
В 1852 он окончил политехникум в Карлсруэ, с 1856 профессор Политехнического института в Цюрихе, в 1864—1896 профессор Промышленного института (позже — Высшая техническая школа) в Берлине. В 1875 впервые четко сформулировал и изложил основные вопросы структуры и кинематики механизмов, которые ранее содержались в неявной форме в работах П. Л. Чебышева и др. Рело дал определение кинематической пары, кинематической цепи и механизма как кинематической цепи принуждённого движения; предложил способ преобразования механизмов путём изменения стойки и путём изменения конструкций кинематических пар. Связал теорию механизмов и машин с проблемами конструирования, например, впервые поставил и пытался решить проблему эстетичности технических объектов. Имея в виду это направление его работ, современники Рело называли его поэтом в технике. Творчество Рело оказало значительное влияние на последующие исследования по теории механизмов. Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции, а также в Мадридском кодексе. (Приложение 1, рис.1).
Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции, а также в Мадридском кодексе. (Приложение 1, рис.1). Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей. (Приложение 2. Рис.3)
Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей. (Приложение 2. Рис.3) 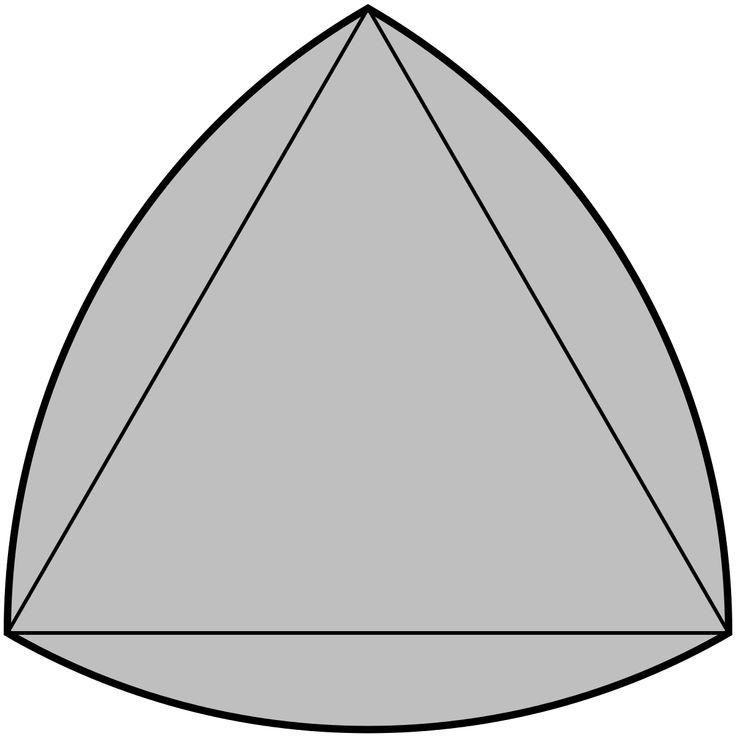 (Приложение 3 рис.4)
(Приложение 3 рис.4)


 Так что возможно, будущее за РПД
Так что возможно, будущее за РПД В Сан-Франциско, для системы рекуперирования воды корпуса люков имеют форму треугольника Рёло. За счет того, что у треугольника Рело площадь меньше, чем у круга, себестоимость люков в форме треугольников Рело была бы ниже, чем у традиционно круглых. Перейдя на серийное производство люков в форме треугольника Рело, на наш взгляд, можно было бы быстрее решить проблему открытых колодцев и избежать травматизма и смертей людей.
В Сан-Франциско, для системы рекуперирования воды корпуса люков имеют форму треугольника Рёло. За счет того, что у треугольника Рело площадь меньше, чем у круга, себестоимость люков в форме треугольников Рело была бы ниже, чем у традиционно круглых. Перейдя на серийное производство люков в форме треугольника Рело, на наш взгляд, можно было бы быстрее решить проблему открытых колодцев и избежать травматизма и смертей людей.
 10)
10) Но, как оказалось, круг – не единственная фигура, которая обладает этим свойством. Вызвавший интерес, треугольник Рело, также принадлежит этому семейству.
Но, как оказалось, круг – не единственная фигура, которая обладает этим свойством. Вызвавший интерес, треугольник Рело, также принадлежит этому семейству.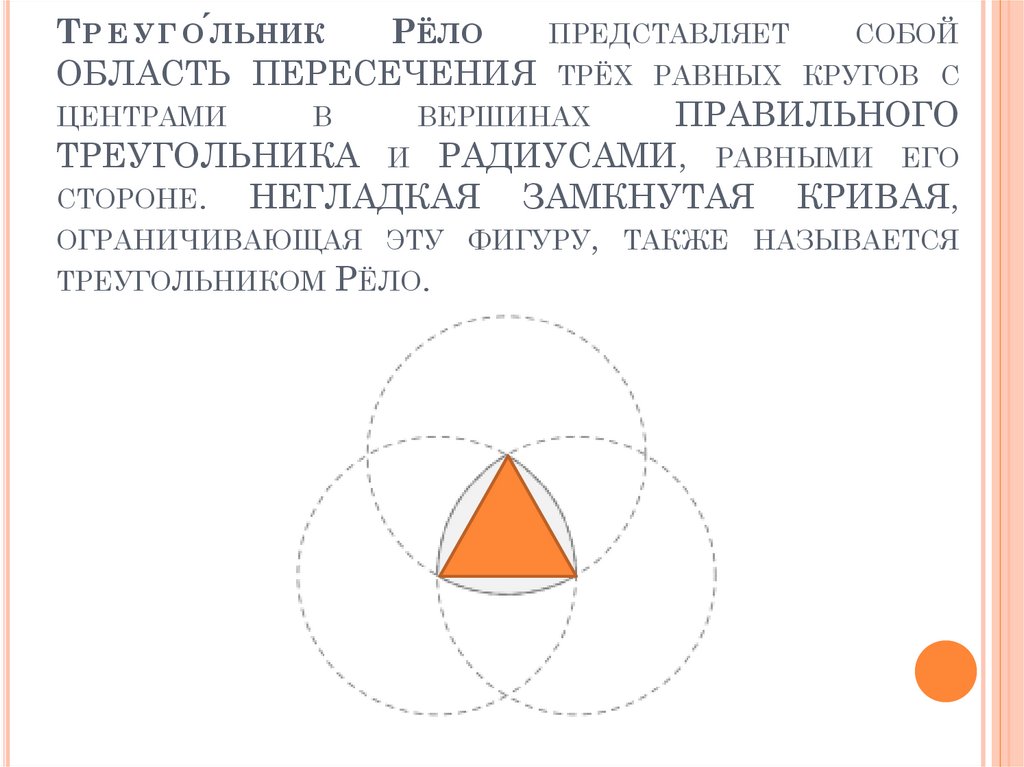
 Числа и фигуры – М., Физматгиз, 1962. -263 с.
Числа и фигуры – М., Физматгиз, 1962. -263 с.