Что такое треугольник Рёло (12 фото) | Екабу.ру
Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло, живший с 1829 по 1905 годы. Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах.
Франц Рёло первым дал доскональные определения понятиям «кинетическая пара», «кинетическая цепь». Он впервые показал возможность связи между основами механики и конструирования.
Иные исследователи первооткрывателем этой фигуры признают Леонарда Эйлер (18 век), который уже тогда продемонстрировал возможность его создания ее из трех окружностей.
А третьи «увидели» треугольник Рёло в рукописях гениального Леонардо Да Винчи. Манускрипты этого естествоиспытателя, с изображением этой «простой» фигуры, хранятся в Мадридском кодексе и в Институте Франции.
Но кто бы ни был первооткрывателем этот «не простой» треугольник получил широкое распространение в современном мире.
А именно:
• Сверло Уаттса. В 1914 году Гарри Джеймс Уаттс изобрел уникальный инструмент для высверливания квадратных отверстий. Это сверло, выполнено в форме Треугольника Рёло;
• Двигатель Ванкеля.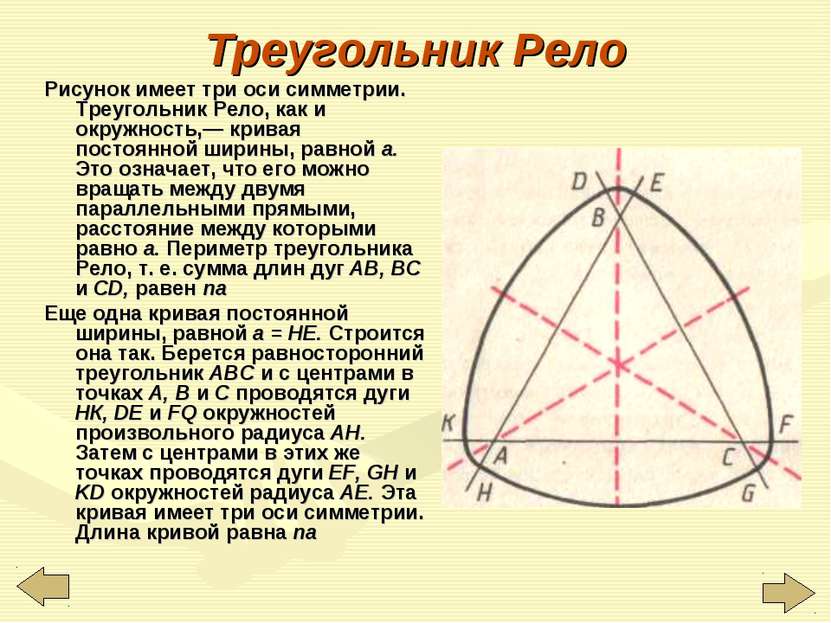
С 1957 года треугольник Рёло немецкий изобретатель Ванкель Ф. создал уникальный механизм. Где внутри камеры, цилиндрической формы, по сложной траектории передвигается ротор-поршень. Созданный в форме треугольника Рёло. При его постоянном движении, каждая его грань, контактируя со стенками камеры, образует сразу три камеры, названные позже «камерами сгорания».
• Грейферный механизм кинопроекторов. Треугольник Рёло, вписанный в квадрат и двойной параллелограмм лежат в его основе. А нужен он для равномерного продергивания кинопленки во время киносеанса со скоростью в 18 кадров/с без отклонений и задержек;
• Основа кулачкового механизма для зигзагообразного шва в швейных машинках, а также в немецких часах таких известных марок как A. Lange & Söhne «Lange 31»;
• Плектр или медиатор, тоже не что иное, как треугольник Рёло. Они необходимы при игре на щипковых музыкальных инструментах.
• В архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля.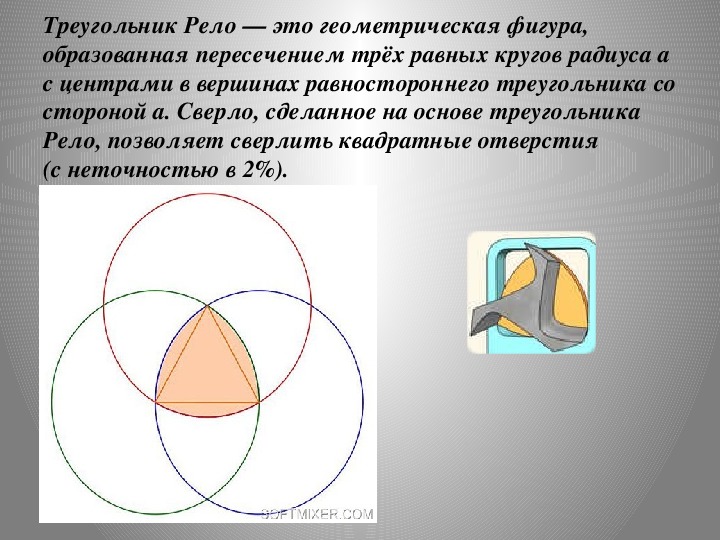
А окна в форме Рёло стоят в Брюгге в церкви Богоматери. Как орнамент он присутствует и на оконных решетках швейцарской коммуны Отрив и цистерцианского аббатства.
На самом деле Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. В частности, он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась.
Леонардо да Винчи, манускрипт A, фрагмент листа 15v
Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции[10], а также в Мадридском кодексе.
Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира.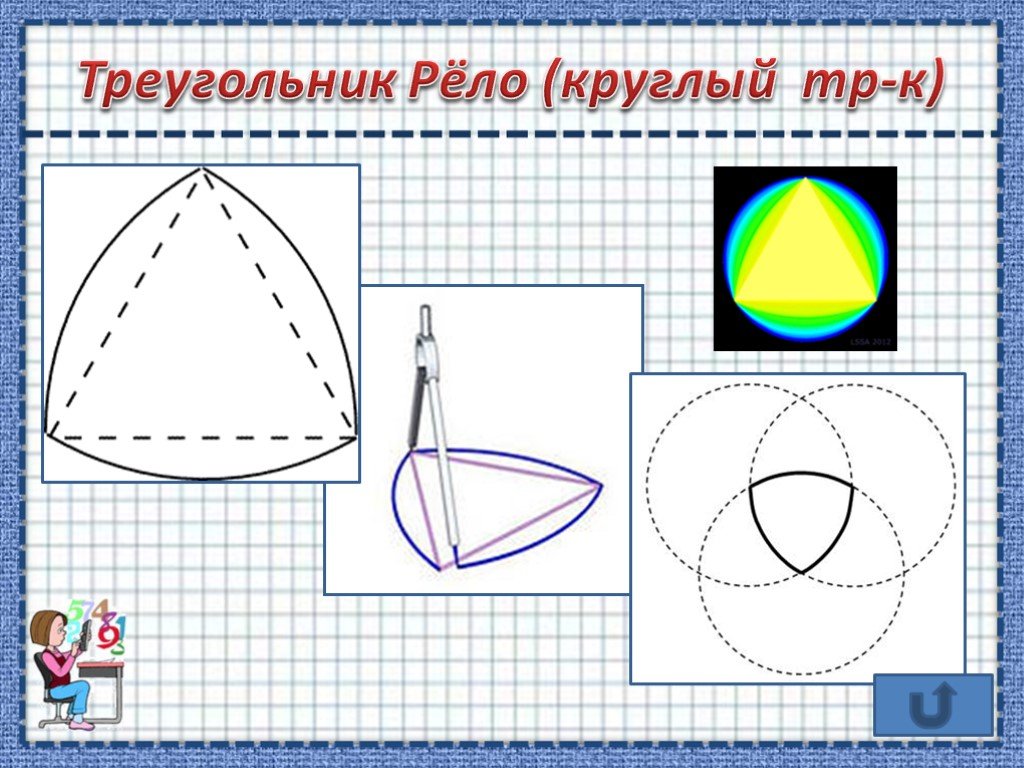
Поверхность земного шара на ней была разделена экватором и двумя меридианами(угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов.
Ещё раньше, в XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон
Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.
Именно треугольник Рело может помочь нам в сверлении квадратных отверстий. Достаточно двигать центр этого «треугольника» по некой траектории, и его вершины начертят почти квадрат, а границы полученной фигуры, за исключением небольших кусочков по углам, будут строго прямыми! Такими, что, если продолжить отрезки, тем самым добавив уголочки, то получится в точности квадрат.
Площадь незаметенных уголочков составляет всего около 2 процентов от площади всего квадрата!
А вот еще применение :
Китайский офицер Гуан Байхуа из Циндао заново изобрел колесо. Он создал необычный велосипед: вместо круглых колес у него треугольник сзади и пятиугольник спереди.
Сам изобретатель уверен, что новая модель будет пользоваться популярностью, поскольку, чтобы передвигаться на таком велосипеде, требуется больше усилий, а значит, это в какой-то степени может заменить спортивную нагрузку.
Добровольцы, опробовавшие новинку, были удивлены тем, насколько ровно передвигается велосипед с новыми колесами. Дело в том, что углы многоугольников сглажены. Это позволяет велосипеду не «прыгать» вверх-вниз, как можно было бы ожидать, поясняет со ссылкой на The Times InoPressa.ru.
Кроме того, колеса по форме являются кривыми постоянной длины, иначе называемыми «многоугольниками Рело» или «круглыми многоугольниками». Контур таких фигур представляет собой плоскую выпуклую кривую, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно «ширине» кривой.
Несмотря на то, что новый велосипед не пользуется коммерческим успехом, Байхуа не унывает. Теперь он занят созданием новой социальной сети в интернете.
Вот еще такое применение:
[источники]
Трегольник Рёло – Математическая шкатулка
Колесо — это предмет, как правило, круглой формы, служащий для передачи или регулирования движения.
Кривые постоянной ширины
Использование колес для перемещения грузов по плоским поверхностям возможно благодаря тому, что все радиусы окружности имеют одинаковую длину. Так как окружность — это геометрическое место точек, равноудаленных от центра. Поэтому если ось вращения колеса проходит через его центр, то она не поднимается и не опускается, а только перемещается вперед или назад, при этом высота над поверхностью остается неизменной. Существует и другой способ перемещения грузов, в котором вместо колес используются валы. Все мы не раз видели на картинках, как огромный каменный блок стоит на нескольких валах и его толкают или тянут веревками
Это возможно благодаря еще одному свойству окружностей, которое не имеет ничего общего с тем, о чем мы только что говорили.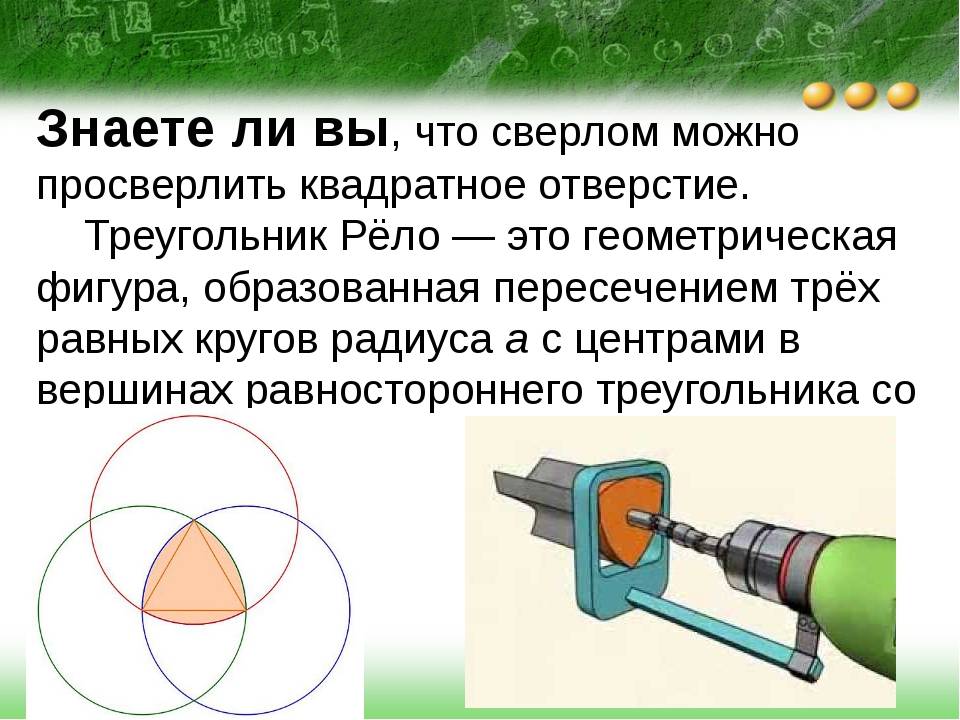
Колеса могут иметь только круглую форму, в то время как форма валов может быть различной.
Свойство, благодаря которому действуют валы, связано не с расположением центра окружности, а с шириной круга, которая постоянна в любом направлении. Рассмотрим в качестве примера эллипс. Ширина эллипса вдоль большой оси очевидно больше, чем вдоль малой оси. Нетрудно представить, что произойдет, если мы подложим под камень валы в форме эллипса.
Камень при движении будет перемещаться вверх-вниз, пока не упадет на землю. Любопытно, но окружность не единственная кривая постоянной ширины. Существует бесконечное множество подобных прямых, которые подчас имеют весьма причудливую форму
Как построить треугольник Рёло
Пусть дан равносторонний треугольник с вершинами А, В и С. Возьмем циркуль и проведем дугу окружности с центром в точке А через вершины В и С. Затем проведем дугу окружности с центром в точке В. Дуга пройдет через вершины С и А. После этого выполним аналогичные действия для вершины С.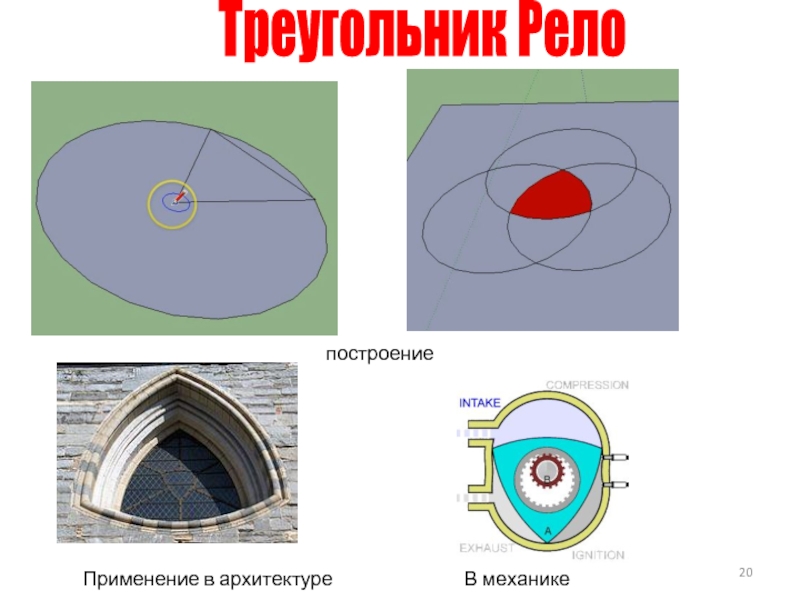
Полученная фигура называется треугольником РЁЛО и является кривой постоянной ширины. Если использовать вал подобной формы, он ничем не будет отличаться от круглого вала. При вращении треугольник Рёло всегда соприкасается с поверхностью земли и блока, поскольку он всегда вращается вокруг одной из вершин, а расстояние от неё до дуги окружности является постоянной величиной
Вершинами треугольника Рёло могут быть скругленными, и при этом он по-прежнему будет обладать постоянной шириной. Чтобы построить такой треугольник, достаточно продлить его стороны на произвольное расстояние, затем, зафиксировав центр окружности в одной из вершин, соединить концы продленных сторон дугами, как показано на рисунке:
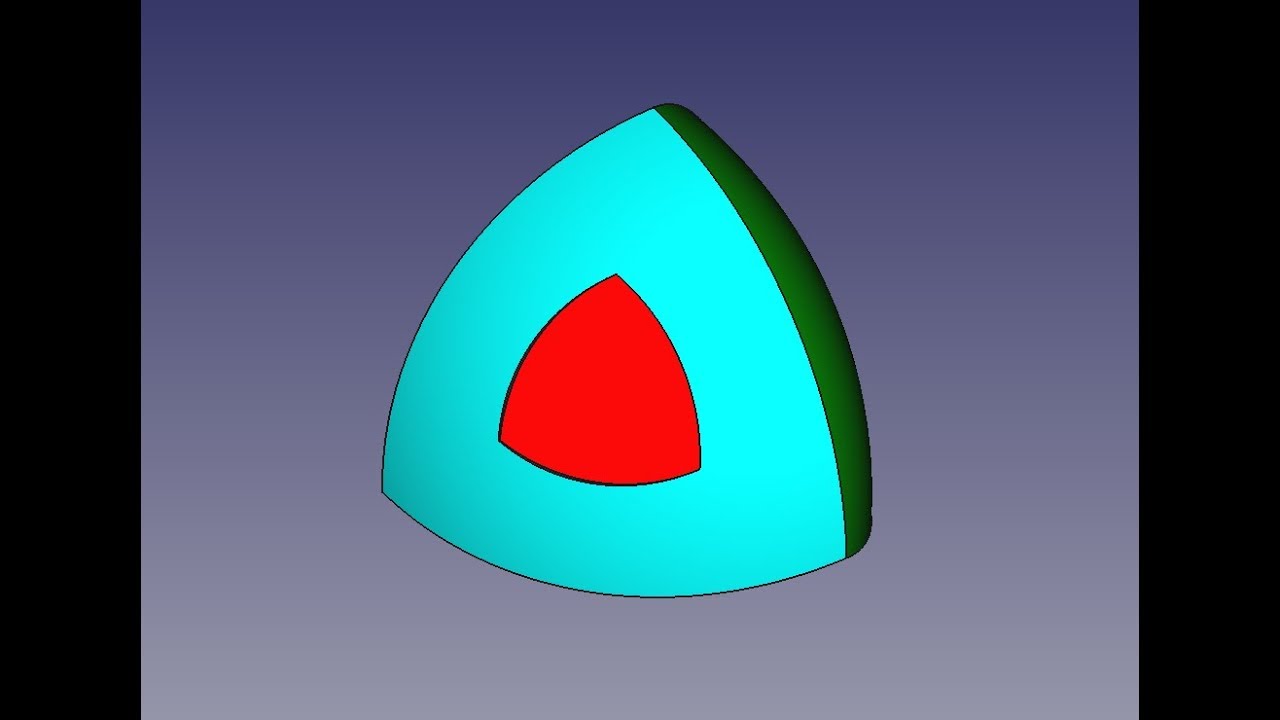
Все вышесказанное можно обобщить и для трех измерений, то есть можно построить геометрические тела постоянной ширины, подобные сфере. Простейшее из них можно получить вращением треугольника Рёло вокруг одной из его осей симметрии. Еще одно подобное тело можно получить, проведя аналогичные построения, но в пространстве: за основу берется пирамида, а не треугольник, и поверх ее граней строятся части сферы.
Полученное тело будет вращаться в пространстве аналогично треугольнику на плоскости
Треуольник Рело: применение
Классические кинопроекторы всегда издают характерный стрекочущий звук. Он возникает из-за использования треугольников Рёло в механизме проектора. При показе фильма на экране на очень короткий промежуток времени (1/24 секунды) показывается кадр, после чего кинопленку необходимо провернуть, чтобы показать на экране следующий кадр. В этот момент затвор должен быть закрыт, чтобы на экране не было расплывчатого изображения. Получается, что движение ленты должно чередоваться с остановками. Это достигается путем равномерного вращения треугольника Рёло вокруг одной из его вершин. Треугольник Рёло находится внутри прямоугольной рамки, которая поднимается и опускается. Рамка остается неподвижной половину периода вращения треугольника, после чего перемещается в новое положение, где остается неподвижной такое же время. Затем весь цикл повторяется
Другое важное применение кривых постоянной ширины основано на возможности построения выпуклой кривой, внутри которой треугольник Рёло может перемещаться так чтобы все его вершины постоянно соприкасались с этой кривой.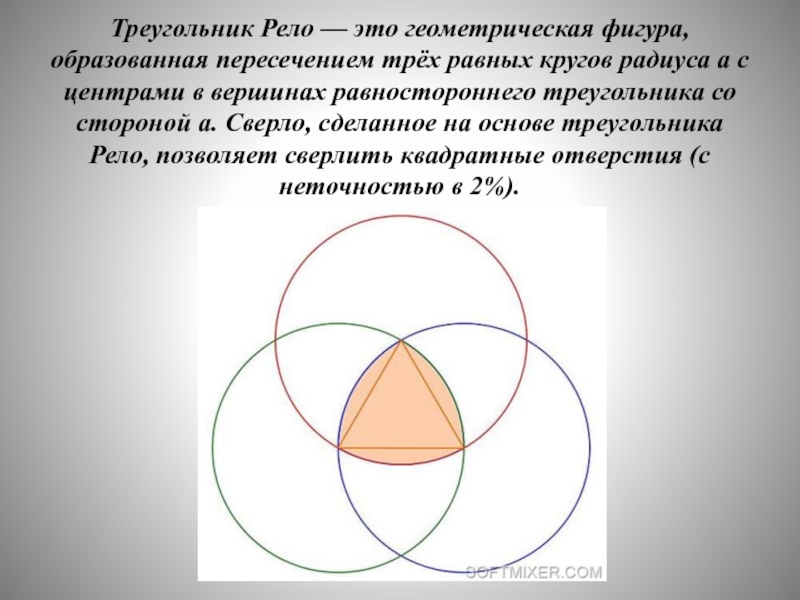
Благодаря этому свойству немецкий инженер Феликс Ванкель в 1924 году спроектировал роторный двигатель, в котором поршни были заменены ротором в форме треугольника Рёло. Ротор вращается внутри кривой необходимых размеров, точно подобранных для корректной работы четырехтактного двигателя внутреннего сгорания. Первый прототип под названием DKM был изготовлен в 1957 году, о результат оставлял желать лучшего из-за сильной вибрации на малой скорости, большого расхода масла и невысокого момента. Сейчас применяется уже третье поколение подобных двигателей (Rx-7), их объём доведен до 1 308 кубических сантиметров, мощность атмосферного двигателя при 8 200 оборотах в минуту составляет 227 лошадиных сил. Классический поршневой двигатель той же мощности будет иметь шесть цилиндров и объём более трех литров
Как сверлить квадратные отверстия?
Можно ли просверлить квадратное отверстие? Здравый смысл подсказывает, что нет, но на самом деле это возможно. В этом нам помогут кривые постоянной ширины.
Представим себе окружность, вписанную в квадрат. При вращении она всегда касается всех его сторон, причем точки касания всегда располагаются на серединах сторон. При вращении треугольник Рёло нужных размеров также может постоянно касаться всех сторон квадрата, но в разных точках, так как его ширина постоянна. Каждая вершина треугольника опишет квадрат со скругленными углами. В начале ХХ века это свойство натолкнуло британского инженера Гарри Джеймса Уоттса на мысль о возможности сверления квадратных отверстий. Добавим, что этот же принцип позволяет сверлить отверстия форме любых многоугольников с четным числом сторон. В сверлильном станке Уоттса центр вращения треугольника Рёло не фиксирован. Описываемая замкнутая кривая выглядит как идеальный квадрат, но в действительности представляет собой более сложную кривую, образованную четырьмя дугами эллипса. Скругленные углы квадратного отверстия также являются дугами эллипса.
Интересный факт о кривых постоянной ширины
Кривые постоянной ширины обладают некоторыми примечательными свойствами.
2, что является минимально возможной.
Франц Рёло
Хотя кривые постоянной ширины были известны с древних времен, треугольники Рёло впервые изучил инженер и математик Франц Рёло (1829-1905), преподаватель Берлинской королевской технической академии. Он выполнил исследование всех механизмов, имевших большое значение в различные моменты истории. За огромный вклад в развитие математики, в 1912 году в Дании ему был установлен памятник.
Подготовка к ОГЭ по математике 2020 — задания 1 — 5 с подробными решениями.
Reuleaux Triangle Png – Бесплатный прозрачный PNG клипарт изображения Скачать
Вы здесь： Скачать клипарт » Треугольник Рело Png
Reuleaux Triangle Png – один из клипартов по теме: черный треугольник, красный треугольник, прямоугольный клипарт. Это изображение клипарта имеет прозрачный фон и формат PNG. Вы можете скачать (1200×1200) Reuleaux Triangle png картинку бесплатно. Это высокое качество и простота в использовании. Кроме того, узнайте больше о абстрактном клипарте, клипарте для обоев, фоновом клипарте.
Пожалуйста, не забудьте поделиться им с друзьями, если хотите.
Отчет DMCA
Обратный поиск изображения
Просмотров: 11
Скачиваний: 1
- Разрешение: 1200×1200
- Название: Треугольник Рело Png
- Лицензия: Личное использование
- Формат файла: PNG
- PNG Размер: 66 КБ
Связанные теги：
абстрактный обои фон геометрический украшение шаблон форма геометрия баннер современный концепция шаблон формы пирамида круг знак аварийной остановки декоративный фон бизнес элемент
Скачать PNGРегистрация не требуется. Неограниченное скачивание!
Граница треугольника Рело имеет постоянную ширину – Треугольник Рело Png 9Треугольник Reuleaux PNG 38
Большое изображение — анимированный Gif Fire Triangle
Предупреждающий знак Клипарт — желтый предупреждающий треугольник0038
5 Star Child Care In Durham Nc Southpoint Mall — Indy Best Of The Triangle
Http — //www — Clker — Com/cliparts — Triangle — Green Triangle Clipart
Xmas Tree — Рождественская елка с треугольником Серпинского
Big Image — Triangle Celtic Knot Png
9 0037 Кельтский треугольник Клип Арт – Треугольник с волнистой линиейБлог налогового юриста Нью-Джерси Cpa – Желтый треугольник с восклицательным знаком
Клип арт гнома – Треугольник0038
Прямоугольный клипарт – Прямоугольный клип Арт
С Днем благодарения Клипарт – Svg Треугольник вправо
Мы можем думать о сбалансированной вешалке как метафоре для – Треугольник Восклицательный знак.
0038Rising Action Clipart – Треугольники в повседневной жизни
Флот восходящего солнца – Треугольник
3 Triangles – Logo 3 Triangles
Бесплатный векторный клип-арт с перевернутым треугольником – Вектор треугольника
Граница треугольника Рело имеет постоянную ширину – Reule aux треугольник Png
вы здесь： Клипарт Скачать » Граница треугольника Рело имеет постоянную ширину – Треугольник Рело Png
Граница треугольника Рело имеет постоянную ширину Это изображение клипарта имеет прозрачный фон и формат PNG. Вы можете скачать (440×440) Граница Треугольника Рело Постоянной Ширины – Треугольник Рело PNG png картинки бесплатно. Это высокое качество и простота в использовании. Кроме того, найдите больше png клипарт о природе клипарт,пи клипарт,время и деньги клипарт. Пожалуйста, не забудьте поделиться им с друзьями, если хотите.
