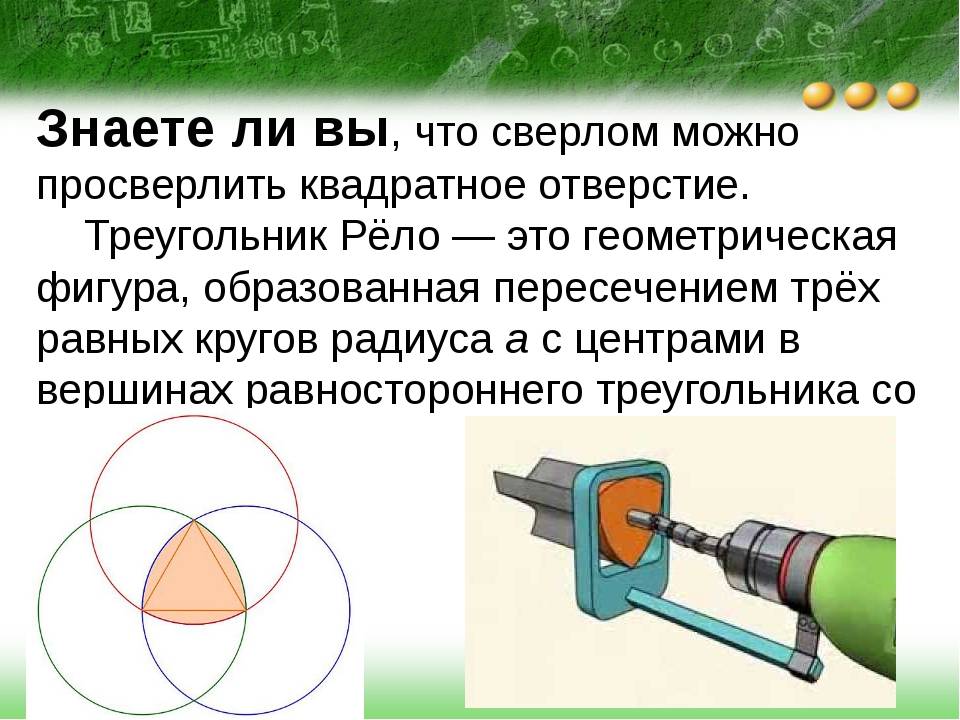
Треугольник Рело (равновеликие фигуры) — Механика — интерактивные экспонаты — Дополнительное образование — Продукция — nau-ra.ru
Треугольник Рело (равновеликие фигуры) — Механика — интерактивные экспонаты — Дополнительное образование — Продукция — nau-ra.ruТреугольник Рело (равновеликие фигуры)
- Продукция
- Дополнительное образование
- интерактивные экспонаты
- Механика
- Треугольник Рело (равновеликие фигуры)
Назначение
Экспонат «треугольник Рело» предназначен для демонстрации колес некруглой формы, сохраняющих параллельность передвигаемых с их помощью предметов земле.
Эксплуатация экспоната
- Извлеките экспонат из транспортировочной упаковки. Проверьте надежность механических соединений.
- Установите две оси с треугольными колесами на нескользящую дорожку.
- Положите на колеса доску.
- Положите ладони плоско на верхнюю доску.
- Перемещайте доску на треугольных колесах и наблюдайте, как она будет перемещаться абсолютно параллельно столешнице.
Подпишитесь на нашу рассылку!
Узнайте о наших новостях, проектах, новинках первыми
Мы открыты для общения
Гарантируем быструю реакцию
на обращения через форму обратной связи
Служба технической поддержки
4s”>Задать вопрос по работе с программой или оборудованием: [email protected]Получить помощь по цифровой лаборатории «
Наураша в стране Наурандии»: +7 (495) 766-24-23, 8 (800) 505-23-48 [email protected]
Вопросы по продукции
Оформить заказ или предложить сотрудничество:
 ru
ru
Мы заботимся о качестве нашей продукции!
{literal}{/literal}Круглый треугольник Рело. Применение математики в реальной жизни
Казалось бы, в этом опыте нет ничего удивительного: колесо (окружность) имеет такую форму, что ему ничего не стоит сохранять постоянную ширину. Однако существуют кривые, не являющиеся окружностями, и, тем не менее, также имеющие постоянную ширину — это треугольники. Однако не простые треугольники, а треугольники Рело, «автором» которых стал французский ученый, посвятивший свою жизнь изучению структуры и кинематики различных механизмов.
Парадоксально, но факт: треугольник — фигура, которая даже по своему звучанию не является «плавной» — кривая постоянной ширины.
Интересно, как же он будет вращаться между зафиксированными планками, постоянно касаясь их!
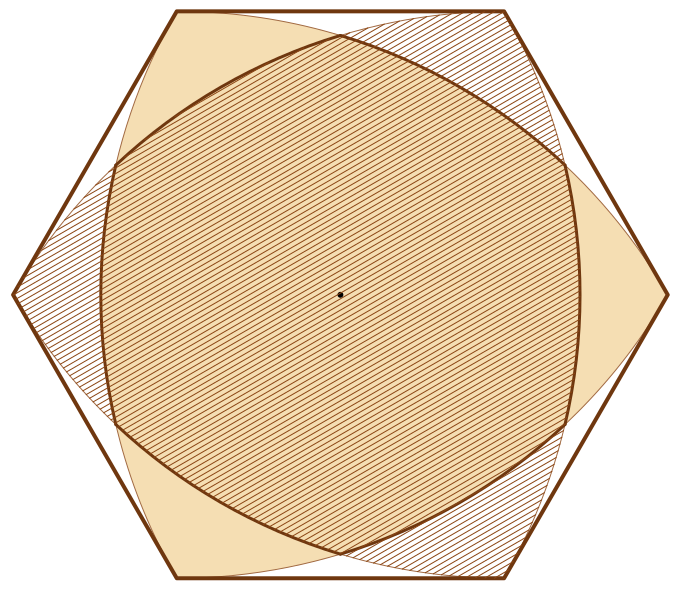
Для того чтобы проверить постоянную ширину треугольника Рело, построим равносторонний треугольник, на каждой стороне которого проведем дугу окружности с радиусом, соответствующем длине стороны.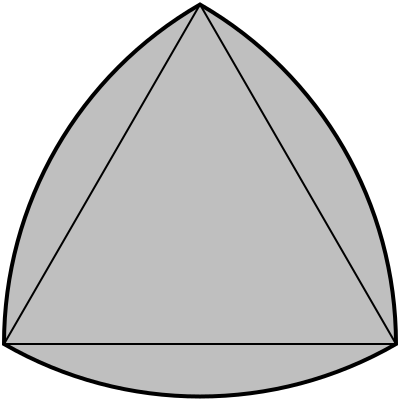 Наш треугольник словно бы вписался в своеобразную кривую, которая и называется круглым треугольником Рело. Проведя две касательные (параллельные планки) и закрепив их так, чтобы избежать смещения, приступаем к вращению треугольника Рело. Нетрудно убедиться, что удивительная фигура все время соприкасается с параллельными планками в двух точках: в «углу» треугольника и в точке, расположенной на противоположной дуге окружности. Следовательно, треугольник Рело — фигура постоянной ширины.
Наш треугольник словно бы вписался в своеобразную кривую, которая и называется круглым треугольником Рело. Проведя две касательные (параллельные планки) и закрепив их так, чтобы избежать смещения, приступаем к вращению треугольника Рело. Нетрудно убедиться, что удивительная фигура все время соприкасается с параллельными планками в двух точках: в «углу» треугольника и в точке, расположенной на противоположной дуге окружности. Следовательно, треугольник Рело — фигура постоянной ширины.
Воспользовавшись описанным выше алгоритмом построения треугольника, можно создать огромное количество кривых постоянной ширины на правильном многоугольнике, имеющем нечетное число углов. В качестве примера достаточно обратить внимание на британский двадцатипенсовик, который представляет собой замкнутую кривую, выполненную на семиугольнике.
А что можно сказать о несимметричных кривых, которые также входят в число кривых постоянной ширины? Попробуем провести похожий опыт: начертим несколько пересекающихся прямых и, выбрав один из секторов, проведем дугу окружности, центр которой будет располагаться в точке пересечения прямых выбранного сектора.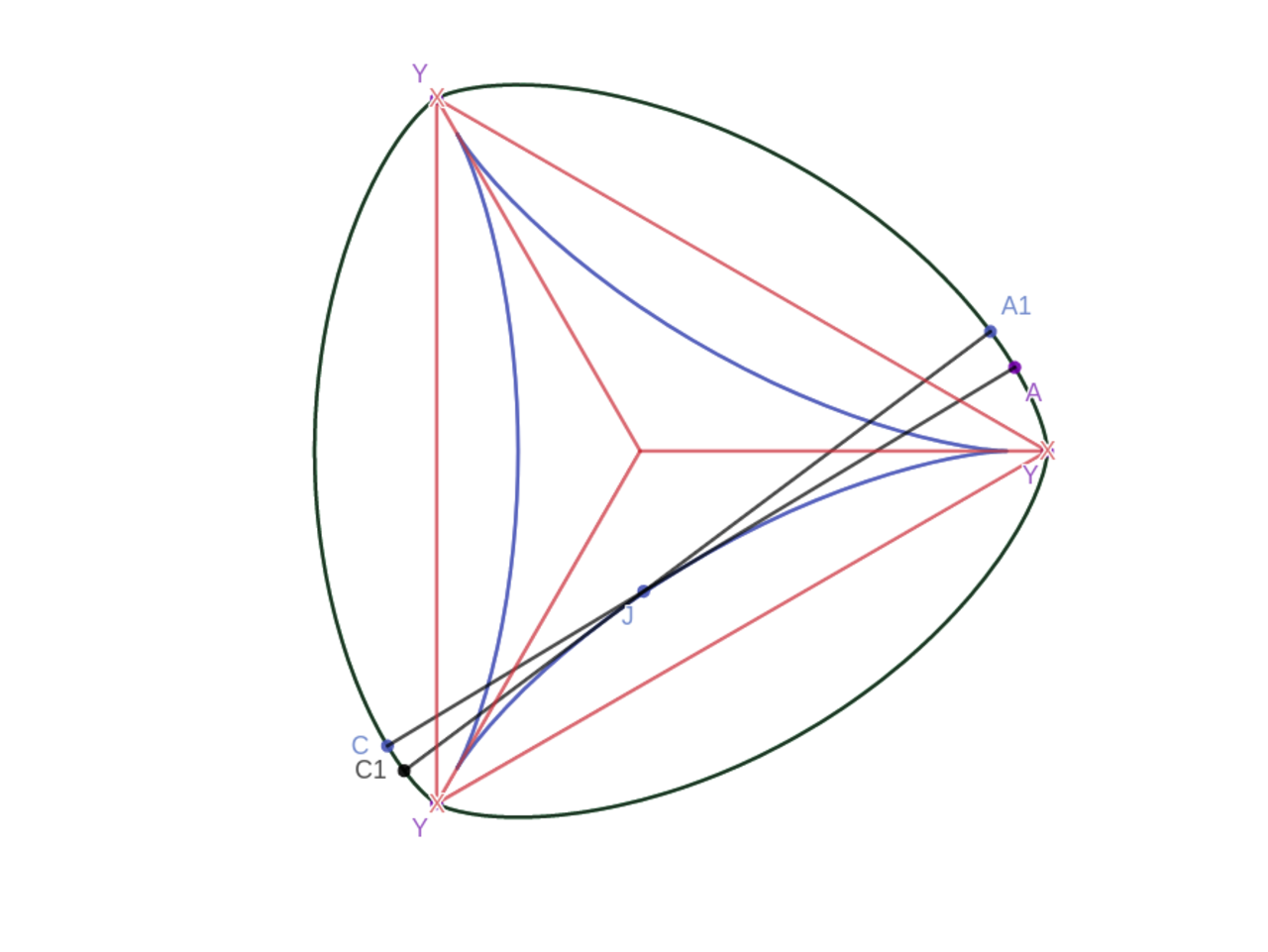 Те же самые манипуляции проделаем и с сектором, расположенным рядом. Следует помнить, что радиус необходимо подбирать таким образом, чтобы непрерывно продолжать уже построенную часть кривой. «Обработав» таким образом все сектора нарисованных нами пересекающихся прямых, мы замкнем кривую и получим еще один наглядный образец кривой постоянной ширины.
Те же самые манипуляции проделаем и с сектором, расположенным рядом. Следует помнить, что радиус необходимо подбирать таким образом, чтобы непрерывно продолжать уже построенную часть кривой. «Обработав» таким образом все сектора нарисованных нами пересекающихся прямых, мы замкнем кривую и получим еще один наглядный образец кривой постоянной ширины.
Несмотря на существующее многообразие кривых постоянной ширины, лишь круг и треугольник Рело занимают в этом классе наиболее почетные места благодаря своим свойствам: окружность способна ограничивать наибольшую, а треугольник Рело — наименьшую площадь.
Если кто-то думает, что треугольник Рело — фигура хоть и удивительная, но абсолютно непрактичная, тот, увы, ошибается. Некоторые автомобили Mazda (RX-7, RX-8) снабжены роторным двигателем Ванкеля, в котором используется треугольник Рело. Благодаря особому устройству роторные двигатели, в отличие от поршневых, считаются наиболее предпочтительными и удобными. Существовавшие ранее кинопроекторы также использовали грейферные механизмы, основанные на треугольнике Рело.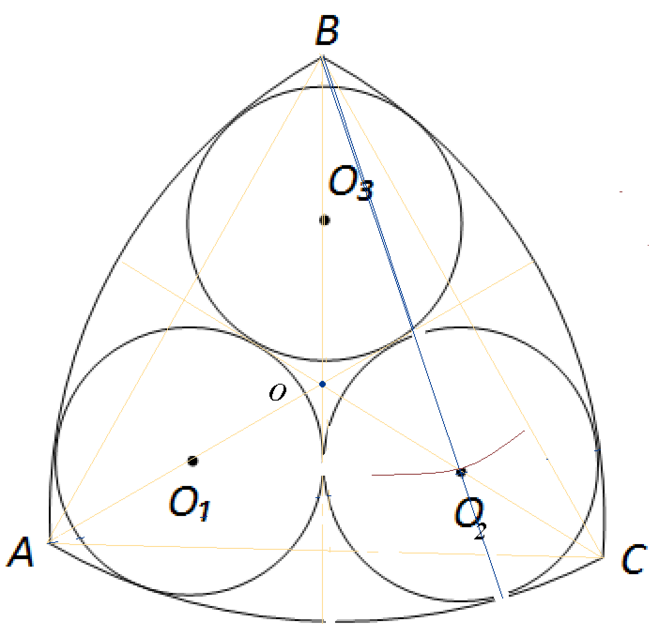 Применение грейферного механизма давало возможность получать четкое изображение и избегать рывков.
Применение грейферного механизма давало возможность получать четкое изображение и избегать рывков.
Поделиться ссылкой
Я выбрал трассу Калифорнийского государственного университета в Нортридже в качестве своего первого
пример. Под каждой картинкой есть примечания.
Теперь вопрос; они измеряли дорожку в 20 см от линии, что означает бордюр находится не в том месте, а полозья бегут примерно на 2/3 метра слишком долго за круг, или они поставили белую линию не в том месте и, возможно, неправильно измерить все остальные линии полосы движения относительно него? Для начала ответить на это является; если дорожка 1 на 10 см шире, чем другие дорожки, значит, они расположены правильно бордюра и (мы предполагаем) правильно измерили 30 см от бордюра. Без вытягивания
из рулетки, на самом деле это знает только тот, кто измерял дорожку
и, возможно, тот, кто хранит данные съемки в файле, возможно, тренер по бегу.
Если установлен рекорд, то речь идет о 9футов на милю, что немаловажно.
Опять же, я говорю это не для того, чтобы придираться к CSUN, это происходит повсюду. Где бы
вы идете, если вы посторонний, кто действительно знает? Без вытягивания
из рулетки, на самом деле это знает только тот, кто измерял дорожку
и, возможно, тот, кто хранит данные съемки в файле, возможно, тренер по бегу.
Если установлен рекорд, то речь идет о 9футов на милю, что немаловажно.
Опять же, я говорю это не для того, чтобы придираться к CSUN, это происходит повсюду. Где бы
вы идете, если вы посторонний, кто действительно знает? Чтобы ответить на вопросы выше для этой конкретной ситуации, я вытащил измерительной лентой и обнаружил, что дорожка 1 такая же широкая, как и другие дорожки. Затем Пришлось делать следующий шаг, я измерил радиус трассы, от бордюра до бордюра (63,46 см) в пределах уровня точности, который можно сделать с помощью измерительной ленты. Этот возможно только потому, что они отметили точку на том же расстоянии от поворот по обеим сторонам дорожки — в данном случае это линия старта на 300 м и общий финиш (без этой информации вы не могли бы быть уверены, что вы были ровно прямыми, край в край).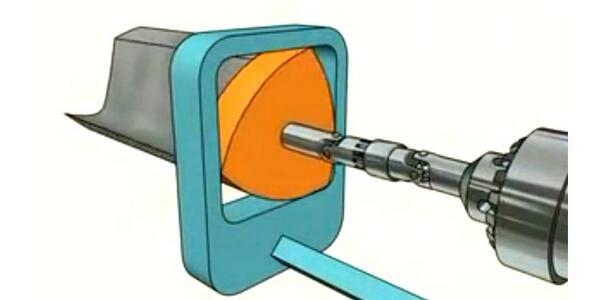 Прибавляем по 20 см с каждой стороны и умножаем
на пи и ответ Прибавляем по 20 см с каждой стороны и умножаем
на пи и ответ 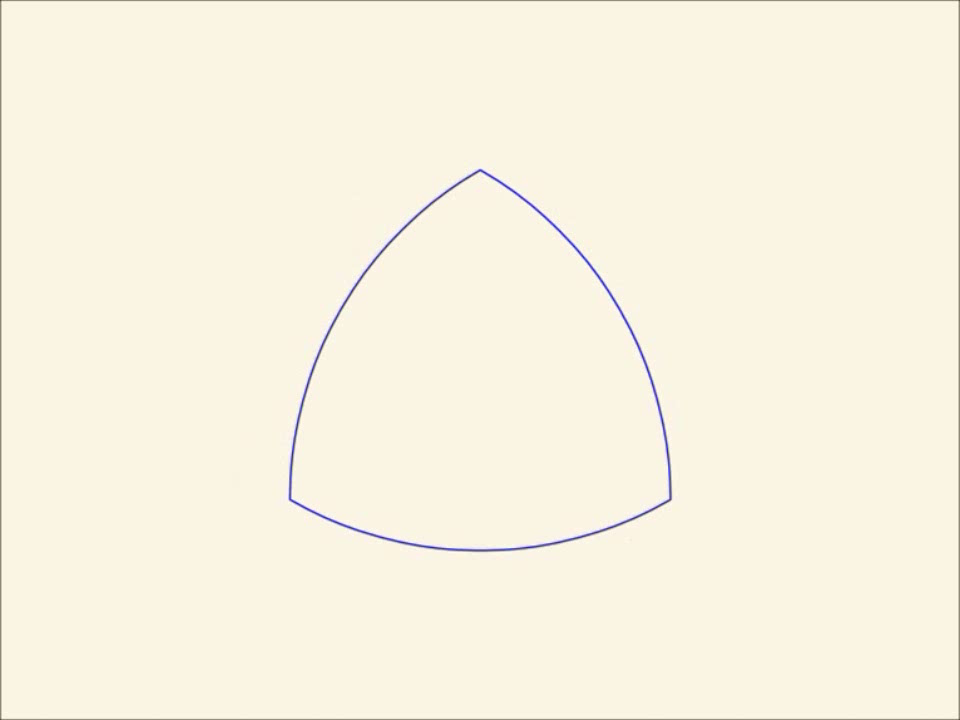 Я, наверное, уже достаточно отредактировал это. Я, наверное, уже достаточно отредактировал это.
|
Треугольная трубка PGRKIT19 Реле
| ||||||||||||||||||||

 в
на переднем плане желоб врезан в склон холма. На 140 м это более прямолинейно
чем необходимо.
в
на переднем плане желоб врезан в склон холма. На 140 м это более прямолинейно
чем необходимо.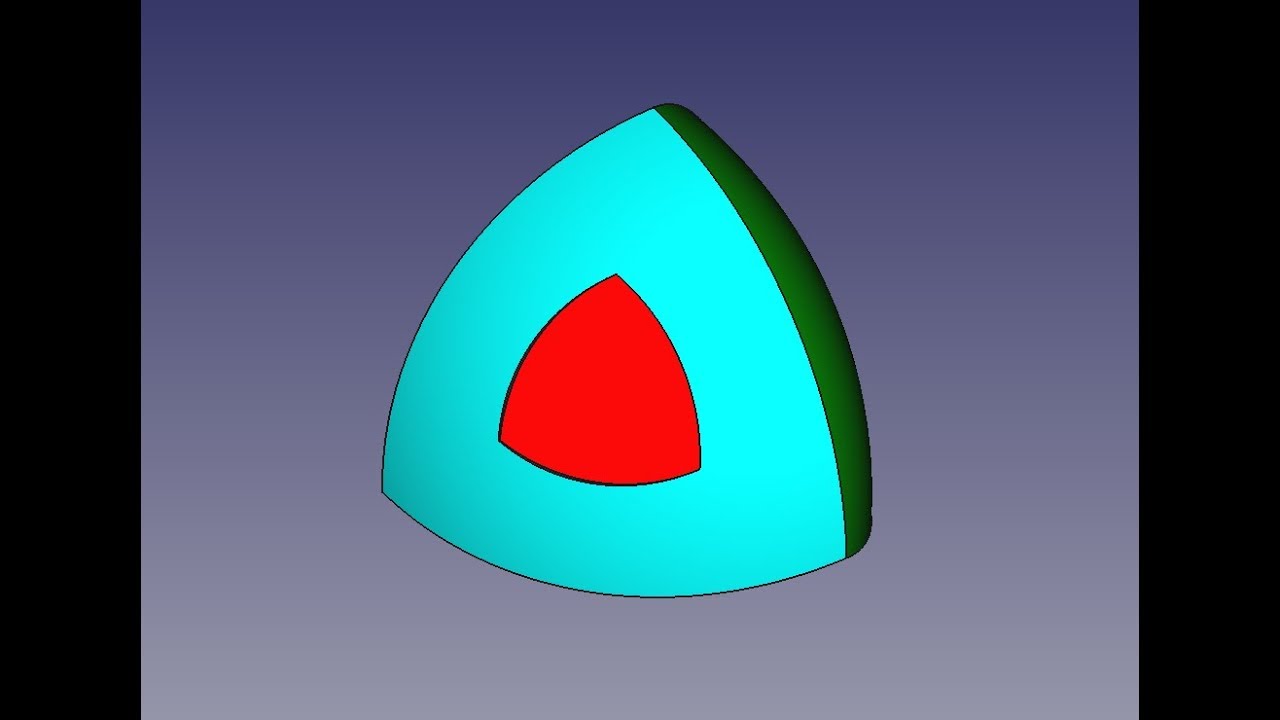 Везде, где используются треугольники, точка
стрелка указывает в зону (но ее размер не указан), плоская сторона
край зоны. Треугольники подряд — это все концы зоны для
обмен 2 и 3. Изогнутая линия – это стартовая линия водопада для круговых гонок.
Он помечен как «10000», потому что это единственная студенческая гонка, которая
старт с такой линии, но это также старт для гонок типа 1600, 3200
или дистанционная комплексная эстафета.
Везде, где используются треугольники, точка
стрелка указывает в зону (но ее размер не указан), плоская сторона
край зоны. Треугольники подряд — это все концы зоны для
обмен 2 и 3. Изогнутая линия – это стартовая линия водопада для круговых гонок.
Он помечен как «10000», потому что это единственная студенческая гонка, которая
старт с такой линии, но это также старт для гонок типа 1600, 3200
или дистанционная комплексная эстафета.  Это два разных
линии для старта двух разных гонок, хотя они взаимозаменяемы
на большинстве дорожек, потому что они так близко, они не взаимозаменяемы. Фотография
Ниже показано, как линии старта на 800 м постепенно удаляются от линии старта.
белые меняют стартовые линии на 200 м, когда вы выходите на дорожки. Черный треугольник
(который должен быть красным) на дорожке 3 это начало второго 4х200 4-го поворота
проходная зона.
Это два разных
линии для старта двух разных гонок, хотя они взаимозаменяемы
на большинстве дорожек, потому что они так близко, они не взаимозаменяемы. Фотография
Ниже показано, как линии старта на 800 м постепенно удаляются от линии старта.
белые меняют стартовые линии на 200 м, когда вы выходите на дорожки. Черный треугольник
(который должен быть красным) на дорожке 3 это начало второго 4х200 4-го поворота
проходная зона. Прямо рядом с ним в полосе 3 находятся реверсивные 200 м и 800 м (должны
быть зеленым) стартовые линии. Линия представляет собой синюю 3-х витковую шахматку. Затем ряд
треугольников, указывающих на конец зоны разгона 4×400. На 1 дорожке
треугольник разделен, наполовину синий, наполовину черный (должен быть красным), чтобы указать на это
знак относится как к 4×400, так и (только на дорожке 1) 4×200. Вокруг
кривая, вы можете видеть, что бордюр находится на белой линии, поднимая вопрос
точности измерения всего трека.
Прямо рядом с ним в полосе 3 находятся реверсивные 200 м и 800 м (должны
быть зеленым) стартовые линии. Линия представляет собой синюю 3-х витковую шахматку. Затем ряд
треугольников, указывающих на конец зоны разгона 4×400. На 1 дорожке
треугольник разделен, наполовину синий, наполовину черный (должен быть красным), чтобы указать на это
знак относится как к 4×400, так и (только на дорожке 1) 4×200. Вокруг
кривая, вы можете видеть, что бордюр находится на белой линии, поднимая вопрос
точности измерения всего трека.
 Многие колледжи отметили 2K, что
по-прежнему применим в дивизионах Masters и Youth.
Многие колледжи отметили 2K, что
по-прежнему применим в дивизионах Masters и Youth. Делает
что-либо в одном и том же месте в течение многих лет приведет к износу. 1 дорожка получает больше всего
использование на сегодняшний день, вот почему большинство треков отговаривают бегунов от использования полосы движения
1. Моя точка зрения такова: шипы от стартовых блоков, безусловно, самые
разрушительная сила (намного больше, чем у толстого бегуна, волочащего свои балетки
вокруг полосы 1).
Делает
что-либо в одном и том же месте в течение многих лет приведет к износу. 1 дорожка получает больше всего
использование на сегодняшний день, вот почему большинство треков отговаривают бегунов от использования полосы движения
1. Моя точка зрения такова: шипы от стартовых блоков, безусловно, самые
разрушительная сила (намного больше, чем у толстого бегуна, волочащего свои балетки
вокруг полосы 1). пунктирная линия — это линия разрыва для этой дорожки, которая снова должна быть зеленой.
На этой трассе есть 100 м прямых (не все), поэтому я не понимаю
почему эта линия на самом деле не в начале прямой здесь – в
факт, что линия старта на 1500 метров измеряется по той же касательной и может
легко служить той же линией. Может быть, они просто хотели, чтобы это было по-другому
линия. Он не выходит на полосу 1, потому что эта полоса не прерывается.
Следует предположить, что все измерения стартовых линий соответствуют
расположение линии разрыва водопада, и теоретически этот разрыв
линия может быть где угодно на прямой, но обычно вы даете
спортсмены максимальное количество прямой к касательной, чтобы сломаться.
пунктирная линия — это линия разрыва для этой дорожки, которая снова должна быть зеленой.
На этой трассе есть 100 м прямых (не все), поэтому я не понимаю
почему эта линия на самом деле не в начале прямой здесь – в
факт, что линия старта на 1500 метров измеряется по той же касательной и может
легко служить той же линией. Может быть, они просто хотели, чтобы это было по-другому
линия. Он не выходит на полосу 1, потому что эта полоса не прерывается.
Следует предположить, что все измерения стартовых линий соответствуют
расположение линии разрыва водопада, и теоретически этот разрыв
линия может быть где угодно на прямой, но обычно вы даете
спортсмены максимальное количество прямой к касательной, чтобы сломаться.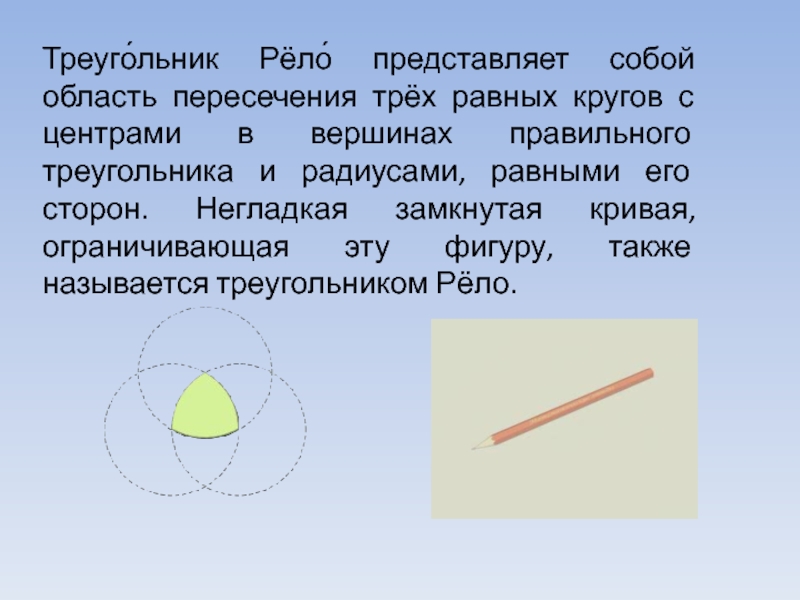 является стартовой линией на 1500 м. Он не так сильно изогнут, как водопад.
на общем финише, потому что у бегунов есть полная прямая, чтобы сломаться
внутрь, поэтому расстояние по касательной к общему маркеру меняется
гораздо меньше от внутренних переулков к внешним переулкам.
является стартовой линией на 1500 м. Он не так сильно изогнут, как водопад.
на общем финише, потому что у бегунов есть полная прямая, чтобы сломаться
внутрь, поэтому расстояние по касательной к общему маркеру меняется
гораздо меньше от внутренних переулков к внешним переулкам. Было бы намного проще
скажите бейсбольной команде, которая работает как бригада, поставить барьер посередине
высоту на каждой зеленой отметке, чем объяснять или определять местонахождение этих отметок для
их.
Было бы намного проще
скажите бейсбольной команде, которая работает как бригада, поставить барьер посередине
высоту на каждой зеленой отметке, чем объяснять или определять местонахождение этих отметок для
их. Едва заметный
черный (должен быть красным) маленький треугольник (прямо над прямоугольником на дорожке 3)
определение зоны ускорения для 4×400. Позади нас этот маленький треугольник
также разделен на полосу 1. Пунктирная линия, отходящая от бордюра, – это бег с препятствиями.
курс, выводящий этих бегунов по дуге через дорожку наружу
прыжок в воду с последующим возвращением их к бордюру.
Едва заметный
черный (должен быть красным) маленький треугольник (прямо над прямоугольником на дорожке 3)
определение зоны ускорения для 4×400. Позади нас этот маленький треугольник
также разделен на полосу 1. Пунктирная линия, отходящая от бордюра, – это бег с препятствиями.
курс, выводящий этих бегунов по дуге через дорожку наружу
прыжок в воду с последующим возвращением их к бордюру. Начинающие организаторы встреч должны усвоить, что требуется время, чтобы заполнить яму
вода, если шланг медленный, это может занять час – спланируйте свой график соответственно.
Фанера под барьером укладывается напротив барьера, чтобы обеспечить
бегуны с восприятием глубины. Бег на скорости в неряшливой мокрой обуви
в состоянии истощения может изменить способность видеть полосу шириной 5 дюймов. Но
правильная постановка ноги на эту перекладину имеет решающее значение для эффективного
перепрыгнуть через воду (или наоборот брутально плюхнуться в нее брюхом). Не ты
не могу просто объехать его – так устроена гонка.
Начинающие организаторы встреч должны усвоить, что требуется время, чтобы заполнить яму
вода, если шланг медленный, это может занять час – спланируйте свой график соответственно.
Фанера под барьером укладывается напротив барьера, чтобы обеспечить
бегуны с восприятием глубины. Бег на скорости в неряшливой мокрой обуви
в состоянии истощения может изменить способность видеть полосу шириной 5 дюймов. Но
правильная постановка ноги на эту перекладину имеет решающее значение для эффективного
перепрыгнуть через воду (или наоборот брутально плюхнуться в нее брюхом). Не ты
не могу просто объехать его – так устроена гонка.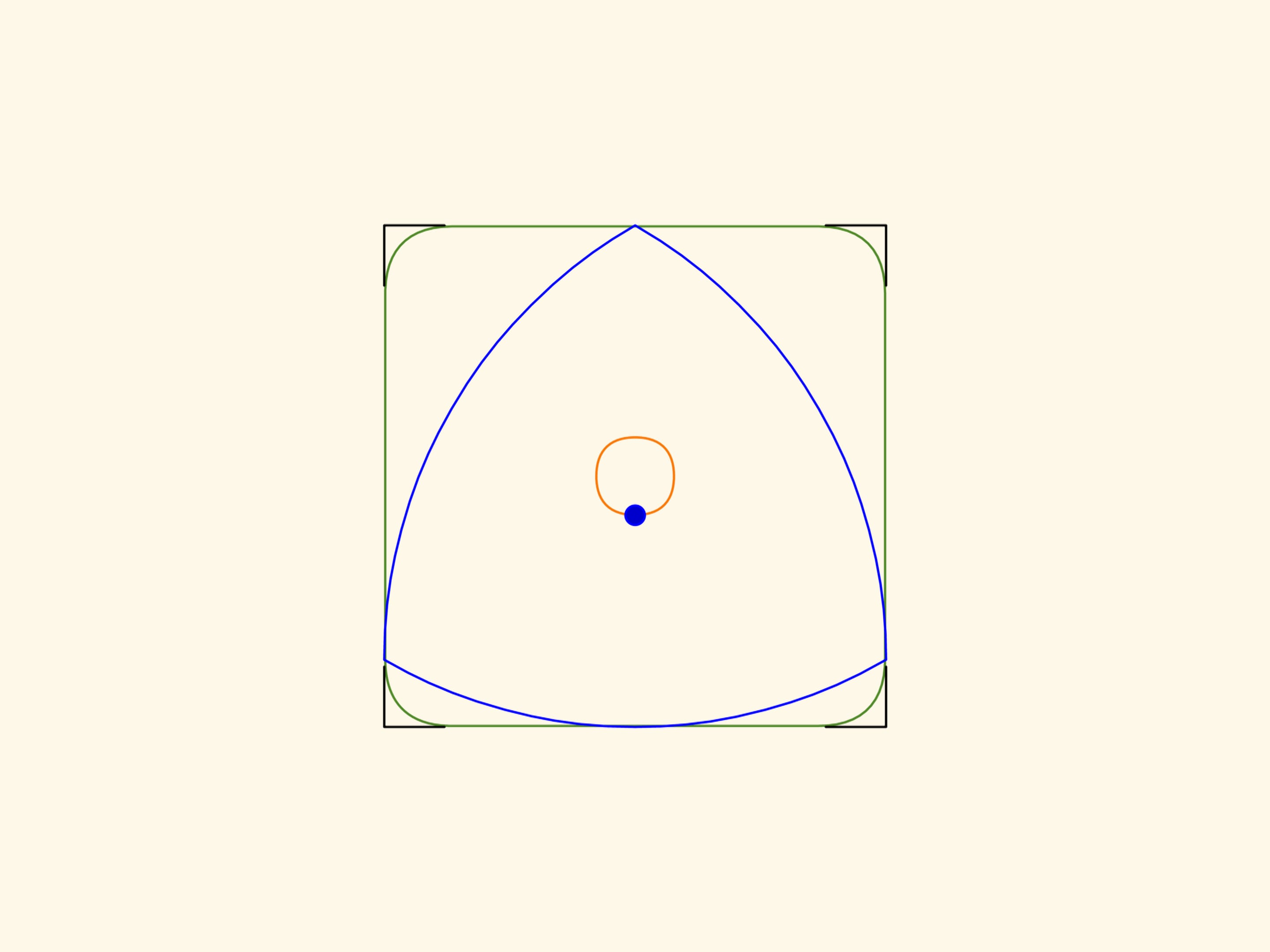 Теперь вот вопрос. понятия не имею, что
синий треугольник здесь на 9-й дорожке. Я предполагаю, что они облажались и покрасили
зона 4×200 имеет неправильный цвет (или, возможно, это фотографическая проблема).
Даже из-за их неправильного цветового кода он должен быть черным (согласно своду правил).
он должен быть красным).
Теперь вот вопрос. понятия не имею, что
синий треугольник здесь на 9-й дорожке. Я предполагаю, что они облажались и покрасили
зона 4×200 имеет неправильный цвет (или, возможно, это фотографическая проблема).
Даже из-за их неправильного цветового кода он должен быть черным (согласно своду правил).
он должен быть красным).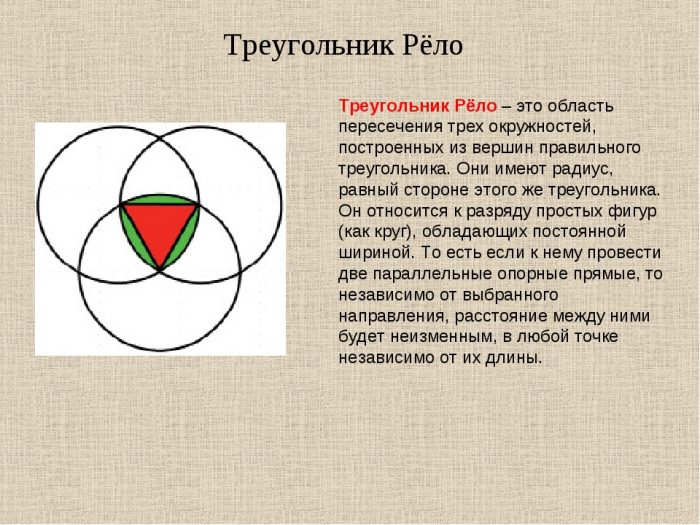 Отсюда
все бегуны даже на последних 100 м до финиша. Опять у них есть
пришлось ремонтировать место где износились стартовые колодки оригинал
поверхность. Обратите внимание на большинство основных стартовых линий для гонок, в которых не участвуют
перерыв, дорожки пронумерованы. Если вы видите линию, нарисованную на
середина конца стрелок 3-й зоны, то есть, наверное, 100 ярдов. Его
здесь нет, но он все еще существует на некоторых старых треках, особенно имперских
треки.
Отсюда
все бегуны даже на последних 100 м до финиша. Опять у них есть
пришлось ремонтировать место где износились стартовые колодки оригинал
поверхность. Обратите внимание на большинство основных стартовых линий для гонок, в которых не участвуют
перерыв, дорожки пронумерованы. Если вы видите линию, нарисованную на
середина конца стрелок 3-й зоны, то есть, наверное, 100 ярдов. Его
здесь нет, но он все еще существует на некоторых старых треках, особенно имперских
треки.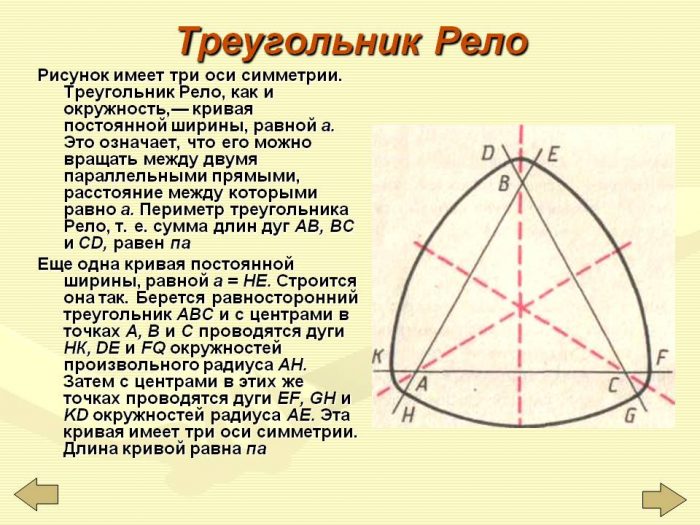 Чем шире повороты или больше смещение вашей финишной черты,
тем больше парашюта вам нужно. В некоторых местах также есть желоб в конце
спринт прямо, но я никогда не слышал дискуссии о том, как финишировать.
Некоторые спортсмены ходят по очереди, даже если есть возможность, другие идут прямо.
даже когда некуда идти, кроме как в соседний переулок.
Чем шире повороты или больше смещение вашей финишной черты,
тем больше парашюта вам нужно. В некоторых местах также есть желоб в конце
спринт прямо, но я никогда не слышал дискуссии о том, как финишировать.
Некоторые спортсмены ходят по очереди, даже если есть возможность, другие идут прямо.
даже когда некуда идти, кроме как в соседний переулок. Столкнувшись с двойными отметками 110H, те, что для этой гонки
всегда те, кто на 1 фут ближе к линии старта. Если вы запускаете шаттл
барьеры без двойных отметок; в обратном направлении (1-й и
3-й этап) сдвиньте стартовую линию на один фут вниз по дорожке в сторону нормали.
линии старта (которая будет заканчиваться на общей линии финиша) и иметь
бегуны с барьерами заканчивают этот этап на один фут дальше обычной стартовой линии. Также в
на переднем плане – водяные пятна на дорожке, свидетельство постоянного сидения
вода из какого-то оскорбительного разбрызгивателя. Красная стрелка в точках расстояния
на линии старта 80 м, которая развивалась за годы бега молодежи и
Мастера встречаются здесь. Его никогда не красили, но он так часто использовался,
остатки ленты, наложенной сюда, оставили постоянную линию. Это 80м
отметка, кстати, всегда находится на отметке 6-й 300H (что, конечно, означает
эта отметка находится на таком же расстоянии от линии финиша).
Столкнувшись с двойными отметками 110H, те, что для этой гонки
всегда те, кто на 1 фут ближе к линии старта. Если вы запускаете шаттл
барьеры без двойных отметок; в обратном направлении (1-й и
3-й этап) сдвиньте стартовую линию на один фут вниз по дорожке в сторону нормали.
линии старта (которая будет заканчиваться на общей линии финиша) и иметь
бегуны с барьерами заканчивают этот этап на один фут дальше обычной стартовой линии. Также в
на переднем плане – водяные пятна на дорожке, свидетельство постоянного сидения
вода из какого-то оскорбительного разбрызгивателя. Красная стрелка в точках расстояния
на линии старта 80 м, которая развивалась за годы бега молодежи и
Мастера встречаются здесь. Его никогда не красили, но он так часто использовался,
остатки ленты, наложенной сюда, оставили постоянную линию. Это 80м
отметка, кстати, всегда находится на отметке 6-й 300H (что, конечно, означает
эта отметка находится на таком же расстоянии от линии финиша).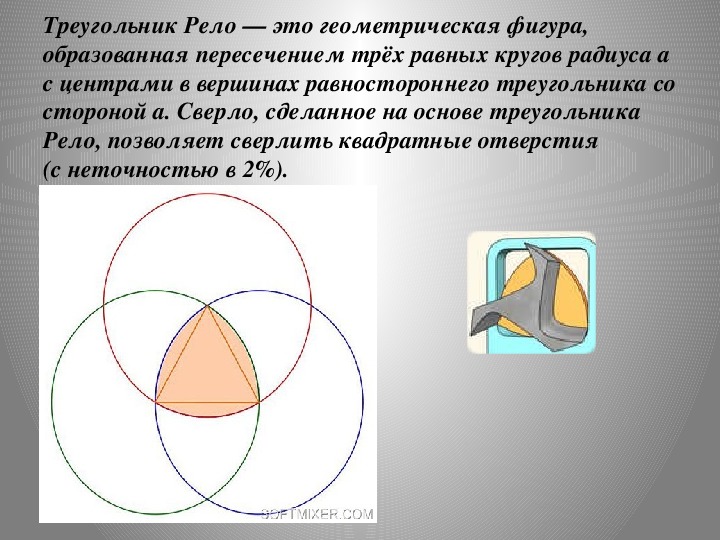 Черная стрела
указывает на слегка изогнутый старт водопада для бега на 3000 метров с препятствиями,
который, поскольку яма находится за пределами трассы, находится на финишной прямой.
Если бы яма находилась внутри поворота, эта линия была бы сзади.
растягиваться, чтобы компенсировать более короткое расстояние на каждом круге.
Черная стрела
указывает на слегка изогнутый старт водопада для бега на 3000 метров с препятствиями,
который, поскольку яма находится за пределами трассы, находится на финишной прямой.
Если бы яма находилась внутри поворота, эта линия была бы сзади.
растягиваться, чтобы компенсировать более короткое расстояние на каждом круге.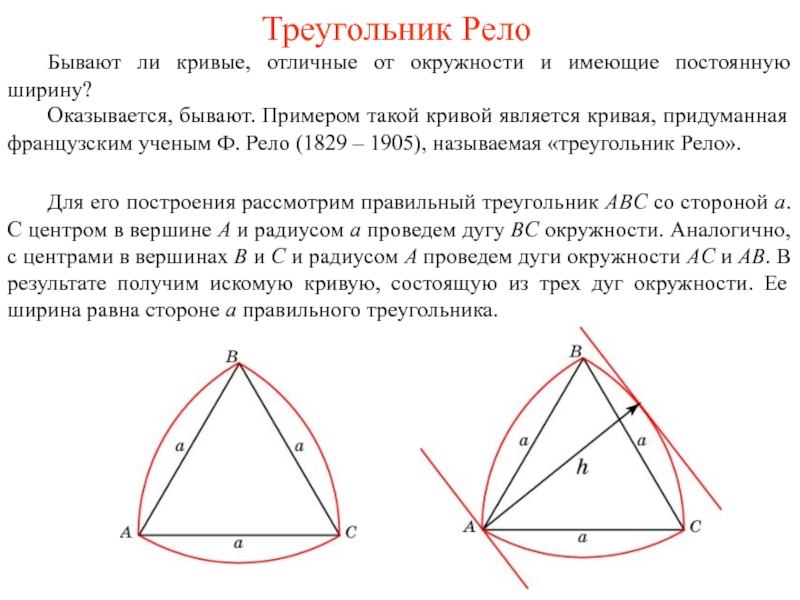 А теперь попробуйте объяснить это футбольной команде. я забежал
гонки на этой трассе, где барьеры были поставлены не в том месте, и вот
причина по которой.
А теперь попробуйте объяснить это футбольной команде. я забежал
гонки на этой трассе, где барьеры были поставлены не в том месте, и вот
причина по которой. Если трек нечетный
расстояние, вещи конечно будут в другом месте, но все же будут
быть относительно друг друга (см. Chaminade HS). Если прямые
Короче говоря, выравнивание может быть труднее воспринять, но если что-то не так
совпадение, то либо вы неправильно идентифицировали линию, либо трек, на котором вы находитесь,
сделал вариацию. Как видно из этого трека, у них четыре разных
линии, которые могут служить финишными линиями. Есть треки, которые могут иметь
разные финишные линии для каждой гонки (см. Gilroy HS). Чем больше они отклоняются
от нормы, тем тяжелее вам разобраться, что они сделали, что
это точка. Если бы люди, которые отмечают следы, следовали бы стандарту и
не изобретать новые способы делать вещи для каждого трека, было бы много
меньше путаницы – этому было бы легче учить. Стандарт есть,
записаны в наши своды правил – все они согласны с тем, что я делаю. я не
писать правила, но эти правила определяют то, как мы работаем в нашем виде спорта, поэтому
каждый получает справедливый и равный шанс провести свое мероприятие.
Если трек нечетный
расстояние, вещи конечно будут в другом месте, но все же будут
быть относительно друг друга (см. Chaminade HS). Если прямые
Короче говоря, выравнивание может быть труднее воспринять, но если что-то не так
совпадение, то либо вы неправильно идентифицировали линию, либо трек, на котором вы находитесь,
сделал вариацию. Как видно из этого трека, у них четыре разных
линии, которые могут служить финишными линиями. Есть треки, которые могут иметь
разные финишные линии для каждой гонки (см. Gilroy HS). Чем больше они отклоняются
от нормы, тем тяжелее вам разобраться, что они сделали, что
это точка. Если бы люди, которые отмечают следы, следовали бы стандарту и
не изобретать новые способы делать вещи для каждого трека, было бы много
меньше путаницы – этому было бы легче учить. Стандарт есть,
записаны в наши своды правил – все они согласны с тем, что я делаю. я не
писать правила, но эти правила определяют то, как мы работаем в нашем виде спорта, поэтому
каждый получает справедливый и равный шанс провести свое мероприятие.