Круглый треугольник Рело / Этюды // Математические этюды
Круглый треугольник Рело / Этюды // Математические этюдыМатематические этюды
К списку
Проектор восьмимиллиметровой киноплёнки «Луч-2». Именно он был в каждом доме, где сами снимали и смотрели киноэтюды.
В этом мультфильме рассказывается, как геометрическое понятие, часто изучаемое на математических кружках, находит применение в нашей повседневной жизни.
Колесо… Окружность. Одним из свойств окружности является ее постоянная ширина. Проведём две параллельные касательные и зафиксируем расстояние между ними. Начнём вращать. Кривая (в нашем случае окружность) постоянно касается обеих прямых. Это и есть определение того, что замкнутая кривая имеет постоянную ширину.
Бывают ли кривые, отличные от окружности и имеющие постоянную ширину?
РЕЛО Франц 1829—1905
РЕЛО Франц (Reuleaux Franz) — немецкий учёный. Впервые (1875) чётко сформулировал и изложил основные вопросы структуры и кинематики механизмов;
разрабатывал проблему эстетичности технических объектов.
Впервые (1875) чётко сформулировал и изложил основные вопросы структуры и кинематики механизмов;
разрабатывал проблему эстетичности технических объектов.
Рассмотрим правильный треугольник (с равными сторонами). На каждой стороне построим дугу окружности, радиусом, равным длине стороны. Эта кривая и носит имя «треугольник Рело». Оказывается, она тоже является кривой постоянной ширины. Как и в случае окружности проведём две касательные, зафиксируем расстояние между ними и начнём их вращать. Треугольник Рело постоянно касается обеих прямых. Действительно, одна точка касания всегда расположена в одном из «углов» треугольника Рело, а другая — на противоположной дуге окружности. Значит, ширина всегда равна радиусу окружностей, т. е. длине стороны изначального правильного треугольника.
В житейском смысле постоянная ширина кривой означает, что если сделать катки с таким профилем, то книжка будет катиться по ним, не шелохнувшись.
Однако колесо с таким профилем сделать нельзя, так как её центр описывает сложную линию при качении фигуры по прямой.
Бывают ли какие-то ещё кривые постоянной ширины? Оказывается, их бесконечно много.
На любом правильном n-угольнике с нечётным числом вершин можно построить кривую постоянной ширины по той же схеме, что был построен треугольник Рело. Из каждой вершины, как из центра, проводим дугу окружности на противоположной вершине стороне. В Англии монета в 20 пенсов имеет форму кривой постоянной ширины, построенной на семиугольнике.
Рассмотренные кривые не исчерпывают весь класс кривых постоянной ширины. Оказывается, среди них бывают и несимметричные кривые. Рассмотрим произвольный
набор пересекающихся прямых. Рассмотрим один из секторов. Проведём дугу окружности произвольного радиуса с центром в точке пересечения прямых,
определяющих этот сектор. Возьмём соседний сектор, и с центром в точке пересечения прямых, определяющих его, проведём окружность.
Все кривые данной постоянной ширины имеют одинаковый периметр. Окружность и треугольник Рело выделяются из всего набора кривых данной ширины своими экстремальными свойствами. Окружность ограничивает максимальную площадь, а треугольник Рело — минимальную в классе кривых данной ширины.
Треугольник Рело часто изучают на математических кружках. Оказывается, что эта геометрическая фигура имеет интересные приложения в механике.
Смотрите, это «Мазда RX-7». В отличие от большинства серийных машин в ней (а также в модели RX-8) стоит роторный двигатель Ванкеля.
Как же он устроен внутри? В качестве ротора используется именно треугольник Рело! Между ним и стенками образуются три камеры, каждая из которых
по очереди является камерой сгорания.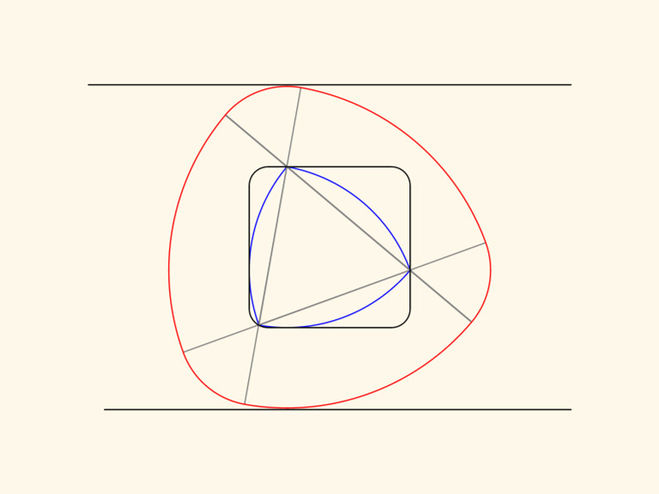 Вот вспрыснулась синяя бензиновая смесь, далее из-за движения ротора она сжимается, поджигается и крутит ротор.
Роторный двигатель лишён некоторых недостатков поршневого аналога — здесь вращение передается сразу на ось и не нужно использовать коленвал.
Вот вспрыснулась синяя бензиновая смесь, далее из-за движения ротора она сжимается, поджигается и крутит ротор.
Роторный двигатель лишён некоторых недостатков поршневого аналога — здесь вращение передается сразу на ось и не нужно использовать коленвал.
А это — грейферный механизм. Он использовался в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было чёткое изображение,
плёнку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть, и так 18 раз в секунду. Именно эту задачу решает
грейферный механизм. Он основан на треугольнике Рело, вписанном в квадрат, и двойном параллелограмме, который не даёт квадрату наклоняться в стороны.
Действительно, так как длины противоположных сторон равны, то среднее звено при всех движениях остаётся параллельным основанию,
а сторона квадрата — всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую
к квадрату фигуру описывает зубчик грейфера.
Вот такие интересные применения, казалось бы, чисто математической задачи используют люди.
Литература
Болтянский В. Г., Яглом И. М. Выпуклые фигуры. — М.—Л.: ГТТИ, 1951.
Радемахер Г., Теплиц О. Числа и фигуры: Опыты математического мышления. — М.: ОНТИ, 1936. — (Библиотека математического кружка; Вып. 10). — [Переиздания: 1938, 1962, 1966, 2020].
Смотри также
Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 84—85, 319—320.
Другие этюды раздела «Кривые (фигуры) постоянной ширины»
Сверление квадратных отверстий Изобретая колесоМатематические этюды
Треугольник Рёло – круглый квадрат или квадратный круг? | Математика не для всех
Применение треугольника Рёло – это отдельная история, которая длится уже сотни лет (смотрите анимации в конце), но об этом позже. Сначала к математическим основам.
Франц Рёло – создатель фигуры. Источник: https://upload.wikimedia.org/wikipedia/commons/e/e6/Franz_Reuleaux.jpgИтак, чтобы построить треугольник Рёло Вам понадобится только циркуль (даже линейка не нужна). Устанавливаете раствор и проводите окружность. Затем ставите циркуль на любую точку и проводите еще одну. После этого ставите циркуль в одну из двух точек пересечения окружностей и проводите третью. Вот, что должно у Вас получится:
Самое главное его свойство – это фигура постоянной ширины наряду, например, с окружностью. Чтобы понять, что такое постоянная ширина необходимо знать понятие опорных прямых.
Опорная прямая – это прямая, содержащая точку фигуры, но не разделяющая никакие две точки на ней. На рисунке выше проведены три пары опорных прямых, расстояние между которыми как раз и равно постоянной ширине треугольника Рёло.
Из всех фигур постоянной ширины треугольник Рёло имеет минимальную площадь (окружность, кстати, максимальную).
Другое экстремальное свойство треугольника Рёло в том, что его углы при вершинах так же минимальны среди всех фигур с постоянной шириной. Посмотрите ни рисунок:
Кстати, существуют треугольники Рёло и с большим количеством угловПроходя через точку а все опорные прямые (а их бесконечность) образуют т.н. пучок, угол между крайними положениями которого и равен углу при вершине треугольника Рёло – 120 градусов. Меньше на плоскости быть просто теоретически не может! Уж такая геометрия.
Однако самое поражающее воображение свойство треугольника Рёло – это возможность вписания его в квадрат с равной стороной! Посмотрите на эту анимацию:
Источник: https://r4.mt.ru/u25/photoBF8C/20734146076-0/original.gifКак видно, вращаясь, треугольник Рёло практически полностью повторяет контур квадрата, что позволяет на его основе делать, например, сверла, которые вырезает близкие к квадратам отверстия:
Т. н. “сверло Уаттса”. Источник: https://s.fishki.net/upload/users/2020/07/01/350879/75d90cdfc2fd8375ed068f1c44dedfcc.gif
н. “сверло Уаттса”. Источник: https://s.fishki.net/upload/users/2020/07/01/350879/75d90cdfc2fd8375ed068f1c44dedfcc.gif“Круглое тащим, квадратное катаем” – этот известный армейский принцип точно не подходит к треугольнику Рёло. Несмотря на углы, колеса такой формы хотя бы на небольших скоростях легко заменят обычные круглые:
Кроме всего прочего, треугольник Рёло использовался в кулачковых механизмах паровых двигателей, т.к. позволяет преобразовывать вращательное движение в возвратно-поступательное.
В специальном роторном двигателе Венкеля, треугольник позволяет выполнять сразу три цикла сгорания топлива в один такт:
Источник: http://rulikolesa.ru/wp-content/uploads/2017/07/5237efc7a8db5813fe95b6fb89446dbca2e967ee.jpgКстати, на данный момент даже есть один автомобиль с такого вида двигателем – это спорт-купе Мазда RX-8, но это – уже совсем другая история.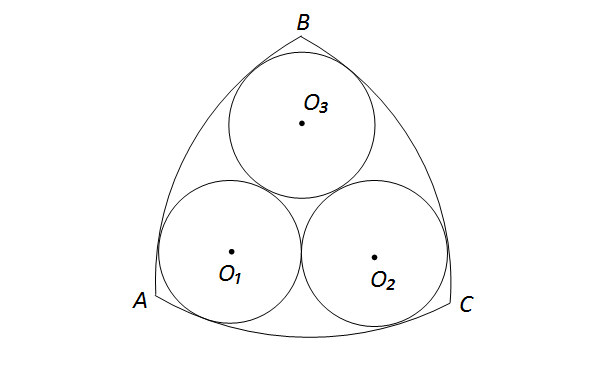 Спасибо за внимание!
Спасибо за внимание!
Поделиться в социальных сетях
Вам может понравиться
Reuleaux Triangle – Прикольные формы, о которых вы никогда не слышали
Формы постоянной ширины
В 1960-х годах парламент Соединенного Королевства принял закон о десятичной валюте, чтобы перевести их валюту в десятичную форму.
Десятичная система счисления — это процесс преобразования денежной системы в систему, основанную на числе десять.
Совет по десятичным валютам (DCB) был создан для наблюдения за этим переходом. Во время перехода DCB рассматривал возможность использования для своих новых монет другой формы, а не круга. Им нужен был дизайн, который легко отличить от других монет на ощупь и на вид. Основным требованием к монете является возможность ее обращения в торговых автоматах. Так появилась идея использовать фигуры постоянной ширины. Кристофер Айронсайд, дизайнер монеты в 50 пенсов, использовал форму равностороннего изогнутого семиугольника. Стороны равностороннего изогнутого семиугольника, как следует из названия, изогнуты, в отличие от правильного семиугольника, который является плоским.
Стороны равностороннего изогнутого семиугольника, как следует из названия, изогнуты, в отличие от правильного семиугольника, который является плоским.
Такой дизайн позволяет слепым и слабовидящим людям различать разные монеты, при этом монета может вращаться так, как если бы она была круглой. Хотя форма выглядит как семиугольник, семиугольник с равносторонней кривизной может плавно вращаться, как круг.
Треугольник Рело
Есть много других форм, которые имеют постоянную ширину. Одной из таких фигур является треугольник Рело.
Формы постоянной ширины имеют одинаковое расстояние между двумя поддерживающими параллельными линиями независимо от их ориентации. Проще говоря, его ширина одинакова во всех направлениях.Окно в форме треугольника Рело в церкви Богоматери 13 века, Брюгге, Бельгия – Предоставлено LEMeZza
Треугольник Рело назван в честь Франца Рело, инженера 19 века, изучавшего его свойства. Треугольник Рело — это просто треугольник с изогнутыми сторонами. Самое интересное в треугольнике Рело то, что он имеет наименьшую площадь и самый острый угол, какой только возможен для фигуры постоянной ширины. Угол при каждом углу треугольника Рело равен 120°. Хотя его название восходит к 19го века, эта форма существовала еще раньше, и ее можно увидеть в архитектуре, предшествующей 19 веку.
Треугольник Рело — это просто треугольник с изогнутыми сторонами. Самое интересное в треугольнике Рело то, что он имеет наименьшую площадь и самый острый угол, какой только возможен для фигуры постоянной ширины. Угол при каждом углу треугольника Рело равен 120°. Хотя его название восходит к 19го века, эта форма существовала еще раньше, и ее можно увидеть в архитектуре, предшествующей 19 веку.
Создание треугольника Рело
- Начертите равносторонний треугольник
- Отцентрируйте циркуль на одном из углов равностороннего треугольника и начертите окружность. Убедитесь, что дуга окружности касается двух других углов равностороннего треугольника.
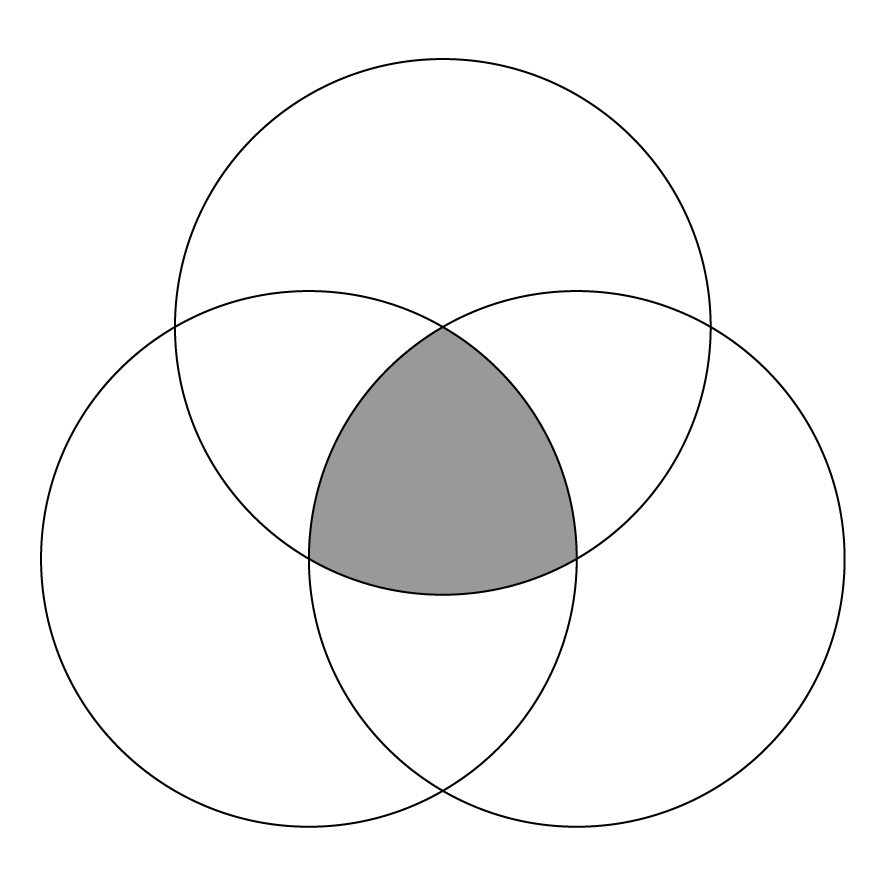
3. Повторите шаг 2 для двух других углов равностороннего треугольника. Заштрихованная область — треугольник Рело.
Как это работает
Перекатывание треугольника Рело – GIF любезно предоставлено Ruleroll В этом эксперименте у вас есть 2 параллельные линии. Расстояние между двумя параллельными прямыми равно ширине треугольника Рело.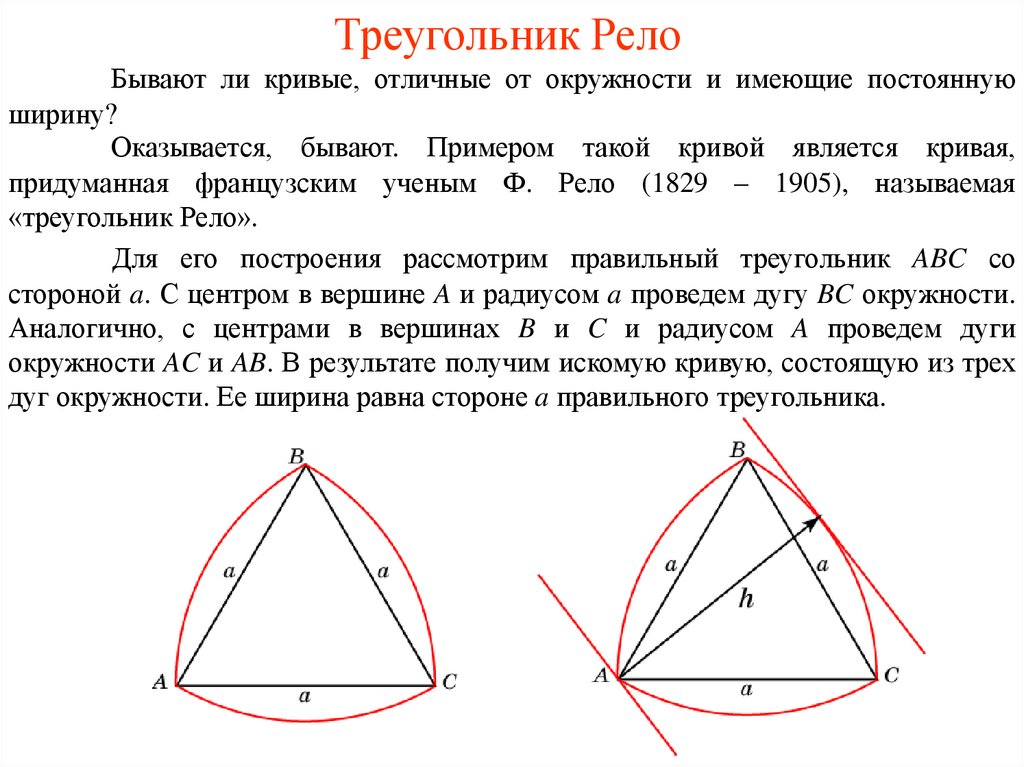 Расстояние между двумя параллельными линиями остается неизменным на протяжении всего эксперимента. В любой момент времени один из углов будет соприкасаться с одной из параллельных линий, в то время как дуга на противоположной стороне этой угловой дуги соприкасается с другой параллельной линией. Видно, что треугольник соприкасается с параллельными прямыми и остается внутри них. Это доказывает, что треугольник Рело имеет постоянную ширину независимо от его ориентации. Поэтому он может плавно катиться, как круг. Видео от Rad-head относительно треугольника reuluax доказывает, что это действительно так.
Расстояние между двумя параллельными линиями остается неизменным на протяжении всего эксперимента. В любой момент времени один из углов будет соприкасаться с одной из параллельных линий, в то время как дуга на противоположной стороне этой угловой дуги соприкасается с другой параллельной линией. Видно, что треугольник соприкасается с параллельными прямыми и остается внутри них. Это доказывает, что треугольник Рело имеет постоянную ширину независимо от его ориентации. Поэтому он может плавно катиться, как круг. Видео от Rad-head относительно треугольника reuluax доказывает, что это действительно так.
Другие свойства
Смещение центроида
Хотя треугольник Рело катится как круг, причина, по которой он обычно не используется, заключается в смещении его центроида при вращении. У кругов есть центроид, который остается неподвижным в центре при вращении. Однако, когда мы прослеживаем вращение треугольника Рело, мы видим, что траектория движения его центроида образует волнообразный узор, как показано на изображении ниже.
У кругов есть центроид, который остается неподвижным в центре при вращении. Однако, когда мы прослеживаем вращение треугольника Рело, мы видим, что траектория движения его центроида образует волнообразный узор, как показано на изображении ниже.
Чтобы колесо треугольника Рело не отклонялось от намеченной траектории, его необходимо закрепить. Однако ось, на которой закреплено колесо, должна иметь возможность свободно перемещаться вверх и вниз, чтобы компенсировать движение центра тяжести.
Видео предоставлено Bicycling Инженер по имени Фил Миллер смог сконструировать велосипед, который едет плавно, несмотря на использование треугольников Рело в качестве колес. Он преодолел эту проблему, позволив передней и задней подвеске велосипеда свободно двигаться в соответствии с ориентацией колеса — простое решение сложной проблемы.
Он преодолел эту проблему, позволив передней и задней подвеске велосипеда свободно двигаться в соответствии с ориентацией колеса — простое решение сложной проблемы.
Вращение внутри квадрата
Вращение треугольника Рело внутри квадрата – изображение предоставлено LEMeZzaКогда треугольник вращается внутри квадрата, он может оставаться внутри квадрата и оставаться в контакте со всеми 4 сторонами квадрата всегда. Обратите внимание, что ось вращения не остается фиксированной в одной точке. Кроме того, центроид делает 3 оборота в противоположном направлении за каждый полный оборот треугольника Рело. Эта концепция сделала применение такой конструкции относительно сложным, поскольку инженеры должны учитывать вращение центроида. Однако инженеры смогли решить эту проблему, включив шестерни и используя уникальные свойства этой формы. Эту конструкцию можно увидеть в роторном двигателе Mazda RX-7.
Роторный двигатель Mazda RX-7.Математика.
Интересный факт:
Отношение длины окружности к ее диаметру равно числу пи.
Интересно, что отношение длины окружности треугольника Рело к его ширине также равно пи.
Заключение
Тетраэдр Рело – Предоставлено JailbirdПодобно сфере и кругу, существует тетраэдр Рело, который является трехмерной формой треугольника Рело. С той же базовой концепцией тетраэдр Рело вращается точно так же, как сфера.
Хотя треугольник Рело существует уже много столетий, он не использовался до тех пор, пока в конце 1900-х годов не появились технологии. Из-за своих уникальных свойств треугольник Рело используется только в очень специфических приложениях, поэтому он также редко используется.
Ссылки
Велоспорт. (2018). Этот парень построил велосипед с треугольными колесами, на котором действительно можно ездить [видео на YouTube]. В YouTube . https://www.youtube.com/watch?v=oobpwxMKD0s
Гарднер, М. (2014). Узлы и кольца Борромео, плитки рептилий и восемь королев: неожиданное повешение Мартина Гарднера (стр. 223–246). Издательство Кембриджского университета; Вашингтон.
223–246). Издательство Кембриджского университета; Вашингтон.
Брайант, Дж., и Сангвин, К. (2011). Насколько круглый ваш круг? : где встречаются инженерия и математика (стр. 191–201). Издательство Принстонского университета.
Ху, X., Ли, Н., и Лю, Б. (2019). Моделирование и применение треугольника Рело в геометрических измерениях – Пекинский научно-технический университет, Пекин . https://iopscience.iop.org/article/10.1088/1755-1315/310/2/022028/pdf
Кункель, П. (2015, 23 октября). Треугольник Рело . Whistleralley.com. http://whistleralley.com/reuleaux/reuleaux.htm
Маор, Э., и Йост, Э. (2014). Красивая геометрия (стр. 154–156). Издательство Принстонского университета.
Объяснение математики. (2020). Reuleaux Triangles — расширение GCSE Higher [YouTube Video]. В YouTube . https://www.youtube.com/watch?v=aDRmbLHyq8A&t=127s
Moon, FC (2007). Машины Леонардо да Винчи и Франца Рело: кинематика машин от эпохи Возрождения до 20 века (стр.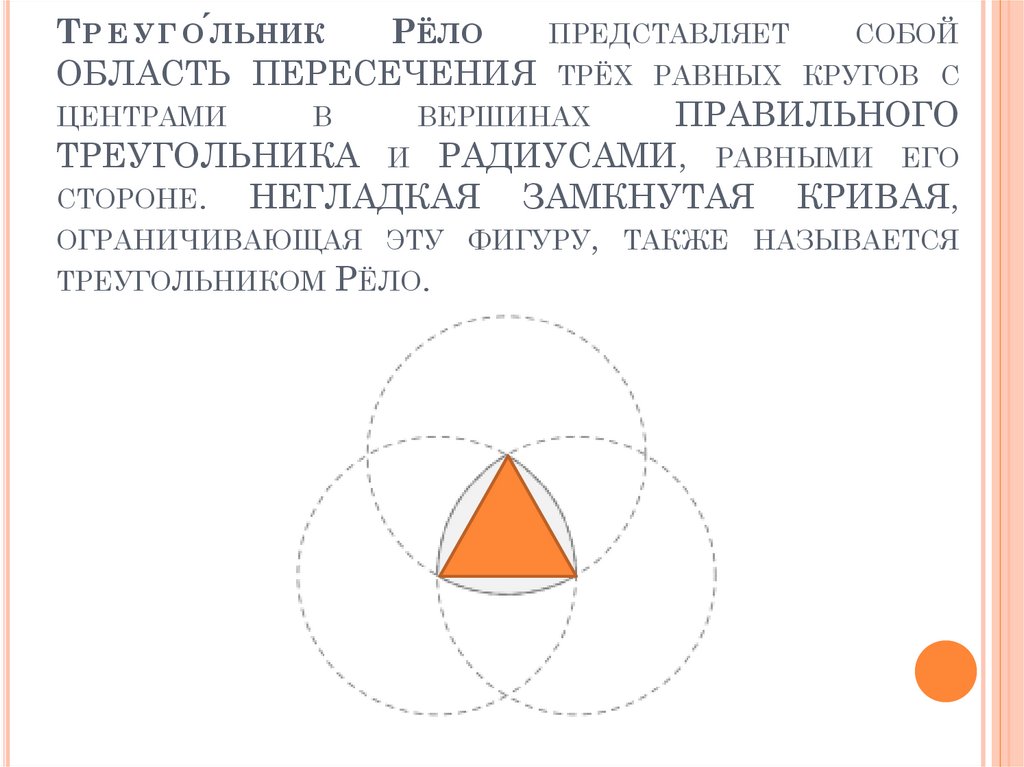 47–59). Спрингер.
47–59). Спрингер.
рад-головка. (2018). Объяснение форм постоянной ширины [видео на YouTube]. В Ютуб . https://www.youtube.com/watch?v=quuw4HC96bE
Королевский монетный двор. (2021). Монеты 50 пенсов . Royalmint.com. https://www.royalmint.com/discover/uk-coins/coin-design-and-specifications/fifty-pence-coin/
РИСУЕМ ТРЕУГОЛЬНИК РЕЛО
РИСУЕМ ТРЕУГОЛЬНИК РЕЛО| На изображении выше треугольник Рело, названный в честь немецкого инженера Франца Рело (1829-1919 гг.).05). Вот формула площади треугольника Рело: . Геометрически говоря, это кривая постоянной ширины. Треугольник Рело — интересная геометрическая фигура, которую легко нарисовать.  1) Возьмите чистый лист бумаги размером 8½ на 11 дюймов. 2) Нарисуйте равносторонний треугольник, выполнив следующие действия: а) В нижней части листа проведите горизонтальную линию длиной 10 см. б) Установите компас точно на радиус 10 см. c) Поместите точку компаса на одном конце линии и начертите дугу над линией. d) Поместите точку компаса на другом конце линии и начертите другую дугу, убедившись, что две дуги пересекаются. |
| д) Используя линейку, проведите линию от скрещенных дуг до одного конца линии внизу (точка А), затем нарисуйте еще одну линию от скрещенных дуг до другого конца линии внизу (точка В). Вы построили равносторонний треугольник. 4) Поместите точку компаса в точку A и начертите полукруг из точки C в точку B. 5) Повторите этот процесс из точки C и точки B, и когда вы закончите, у вас получится треугольник Рело! |
Если у вас есть компьютер с Windows, у вас будет доступ к программе под названием Microsoft Paint. 1) Откройте Microsoft Paint, чтобы создать новую графику. Просто чтобы убедиться, что у вас достаточно места, установите размер изображения примерно 1400 на 800 пикселей. Установите цвет изображения на черный, щелкните значок «круг» и измените размер на 1 пиксель. 2) Переместите мышь в верхнюю часть страницы, пока не увидите цифры в левом нижнем углу: 500, 0. Пока вы находитесь на отметке 500, 0, нажмите левую кнопку мыши и, удерживая ее, переместите ее, пока числа в нижнем левом углу читаются как 1001, 500. В этот момент отпустите кнопку мыши, и у вас должно получиться изображение, похожее на это: . 4) Нажмите кнопку мыши и, удерживая ее, переместите мышь в положение 876, 712, затем отпустите кнопку мыши. 5) Ваша графика должна теперь выглядеть так: 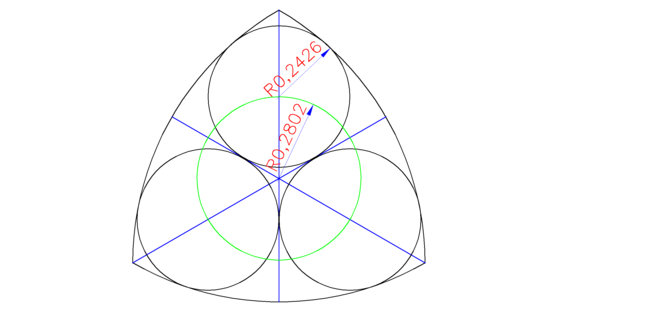 |

 Интересно, что отношение длины окружности треугольника Рело к его ширине также равно пи.
Интересно, что отношение длины окружности треугольника Рело к его ширине также равно пи.  Да, он поставляется бесплатно с Windows, и его более чем достаточно для рисования треугольника Рело.
Да, он поставляется бесплатно с Windows, и его более чем достаточно для рисования треугольника Рело.