Деревообрабатывающий станок Электромаш Тирасполь УБДН-6М (6 операций), цена 7480 грн
Многофункциональный станок УБДН 6М имеет очень широкие возможности работы , связанные с работой по дереву. Станок производится в Тирасполе и имеет расшифровку как “Устройство бытовое настольное деревообрабатывающее”
Станок деревообрабатывающий Електромаш – это устройство, предназначенное для обработки древесины, пластмассы,металла позволяет выполнять такие операции: продольную и поперечную распиловку заготовок, распиловку под углом, фугование пиломатериалов с максимальной шириной обработки поверхности до 200 мм, токарную обработку деревянных заготовок, фрезерно-сверлильные работы, фасонное фрезерование деревянных заготовок, заточку инструмента. Станок многофункциональный имеет отличительные конструктивные и технические характеристики.
1. Фугование:
- Ширина обрабатываемой поверхности 200 мм;
- Толщина снимаемого слоя от 0,2 до 3 мм;
2.
- Толщина заготовки не более 55 мм;
- Наибольшая глубина пропила 55 мм;
- Диаметр пилы 200 мм;
3. Сверление и фрезерование:
- Диаметр хвостовика инструмента не более 13 мм;
4. Токарная обработка:
- Диаметр заготовки не более: 70 мм;
- Длина заготовки не более: 420 мм;
5. Фрезерование фасонными фрезами:
- Ширина ножа не более 40 мм;
6. Заточка инструмента:
- Диаметр шлифовального круга 125 мм;
Особенности:
- Относительно небольшие размеры;
- Возможность применения в настольном исполнении;
- Сбор опилок;
- Возможность включения в розетки, не имеющие заземления.
Технические характеристики:
- Мощность двигателя – 1500 Вт;
- Максимальная глубина пропила – 55 мм;
- Максимальная толщина строгания – 0,2-3 мм;
- Максимальная ширина строгания – 200 мм;
- Чистло оборотов – 3500 об/мин;
- Диаметр дисковой пилы – 200 мм;
- Ширина ножа для строгания – 200 мм;
- Габариты – 455*355*498 мм;
- Вес – 55 кг.

Станок деревообрабатывающий Могилев УБДН 1-05
Станок деревообрабатывающий Могилев УБДН 1-05 (Техноприбор) предназначен для регулярного использования при обработке древесных материалов в быту или на производстве.Данная модель легко справится с продольным и поперечным распилом древесины, фугованием древесных материалов с максимальной шириной захвата до 250 мм включительно.
Надежный двигатель имеет мощность 2200 Вт, что позволяет обеспечивать максимально производительный рабочий процесс. Обязательно обратите ваше внимание на наличие в комплекте поставки прижимного устройства.
Многофункциональный деревообрабатывающий станок Могилев УБДН 1-05 2,2 кВт соответствует наилучшим стандартам и обладает набором всех самых необходимых функций. Весь инструмент от торговой компании Могилев это проверенное временем качество и надежность. Профессионалы выбирают Могилев
Профессионалы выбирают Могилев
Купить станок деревообрабатывающий Могилев УБДН 1-05 с официальной гарантией 1 год вы можете в нашем интернет магазине Дачник.
Особенности Могилев УБДН 1-05:
- Защитный кожух для каждой части
- Асинхронный двигатель
- Тепловое реле
- Двойная изоляция
- Компактные размеры
- Высокие обороты
- Прочные обмотки
Характеристики Могилев УБДН 1-05:
- Номинальная мощность двигателя: 2.2 кВт
- Номинальная потребляемая мощность станка не более: 2.9 кВт
- Род тока: переменный однофазный
- Частота вращения вала: 5000 об/мин
- Наибольшая толщина распиливаемого материала: 70 мм
- Максимальная глубина строгания за один проход: 3 мм
- Наибольшая ширина строгаемого материала: 235 мм
- Наибольшая ширина строгаемого материала с использованием прижимного приспособления: 250 мм
- Наибольшая глубина строгания за один проход: 4 мм
- Длина рабочего стола (подвижного и неподвижного) при строгании не менее: 390 мм
- Ширина рабочего стола при строгании не менее: 240 мм
- Длина пильного стола не менее: 870 мм
- Ширина пильного стола не менее: 410 мм
- Габаритные размеры (длина x ширина x высота), мм: 950х570х460
- Масса без комплекта принадлежностей, не более, кг: 48
Комплектация Могилев УБДН 1-05:
- Станок деревообрабатывающий Могилев УБДН 1-05
- Инструкция
- Гарантийный талон
Гарантия 12 мес.
Осуществляем доставку Деревообрабатывающих станков по всем городам и регионам Украины
Киев, Харьков, Одесса, Днепропетровск, Донецк, Запорожье, Львов, Кривой Рог, Николаев, Мариуполь, Луганск,Винница, Макеевка, Севастополь, Симферополь, Херсон, Полтава, Чернигов, Черкассы, Житомир, Сумы, Хмельницкий, Черновцы, Горловка, Ровно, Днепродзержинск, Ивано-Франковск, Кременчуг, Тернополь, Луцк, Белая Церковь, Краматорск, Борисполь, Керчь, Никополь, Славянск, Ужгород, Бердянск, Алчевск, Павлоград, Северодонецк, Евпатория, Лисичанск, Каменец-Подольский, Бровары, Ирпень, Вишневое, Боярка, Буча и другие.
Купить Деревообрабатывающий станок с доставкой по Украине можно в нашем интернет-магазине “Дачник”.
Деревообрабатывающий станок Электромаш УБДН-6М [Тирасполь, Оригинал]
Универсальный деревообрабатывающий станок
Электромаш УБДН-6М
Деревообрабатывающий станок Электромаш УБДН-6М – однофазное оборудование, предназначенное для продольного и поперечного пиления, а также пиления под углом, строгания по плоскости, по ребру и под углом. В модели просутствует возможность токарной обработки деревянных заготовок. Распиловочный диск закрыт кожухом, что исключает вылетание опилок в оператора. Станок отличается высокой производительностью и имеет широкую область применения как в быту, так и на небольших производственных предприятиях. Ножи установлены на вал станка.
В модели просутствует возможность токарной обработки деревянных заготовок. Распиловочный диск закрыт кожухом, что исключает вылетание опилок в оператора. Станок отличается высокой производительностью и имеет широкую область применения как в быту, так и на небольших производственных предприятиях. Ножи установлены на вал станка.
Ключевые особенности:
- Большая мощность и производительность
- Высокая точность исполняемых работ
- Вентиляционные отверстия способствуют своевременному оттоку тепла от двигателя агрегата и увеличивают его срок службы
- Возможность выполнения различных работ на одном станке
Технічні характеристики:
- Мощность: 1500 Вт
- Максимальное количество оборотов: 3500 об / мин
- Возможние работы: фугование, распиловка, фрезерование, токарная обработка
- Максимальная ширина строгания: 200 мм
- Глубина строгания: 0.2 – 3 мм
- Максимальный диаметр диска: 200 мм
- Максимальная глубина резки под углом 90°: 75 мм
- Максимальная глубина фигурной резки: 55 мм
- Максимальный диаметр хвостовика инструмента: 13 мм
- Максимальный диаметр заготовок при токарной обработке: 70 мм
- Максимальная длина заготовок при токарной обработке: 420 мм
Комплектация:
- Деревообрабатывающий станок Электромаш УБДН-6М
Официальная гарантия от производителя: 12 мес
* Внешний вид инструмента и комплектация может отличаться от приведенного на рисунке. Это вызвано дальнейшим техническим усовершенствованием модели. Производитель оставляет за собой право вносить изменения в конструкцию, комплектацию, внешний вид, техническое и програмное обеспечение товара, не ухудшая качество изделия, без предварительного уведомления пользователя, с целью повышения его потребительских качеств. Магазин не несет ответственность за изменения, внесенные производителем.
Это вызвано дальнейшим техническим усовершенствованием модели. Производитель оставляет за собой право вносить изменения в конструкцию, комплектацию, внешний вид, техническое и програмное обеспечение товара, не ухудшая качество изделия, без предварительного уведомления пользователя, с целью повышения его потребительских качеств. Магазин не несет ответственность за изменения, внесенные производителем.
Универсальный станок по дереву УБДН-6М
Особенности
- Мощный, вентилируемый, асинхронный двигатель.
- Регулируемый стол для фугования заготовок.
- Быстро перенастраивается с одной операции на другую.
- Для получения ровной и чистой поверхности на фуганке установлены 3 регулируемых ножа.
- Для выполнения продольной и поперечной распиловки в комплект входит пила 32х200мм.
- Выборка пазов происходит с помощью фрезы барабанного типа со сменными ножами.
- Для фрезерования концевыми фрезами используется сверлильный патрон, который можно использовать для шлифования заготовок.

Какие операции можно выполнять?
- Продольная и поперечная распиловка;
- Распиловка под углом;
- Фугование;
- Токарная обработка;
- Фрезерно-сверлильные работы;
- Фасонное фрезерование деревянных заготовок;
- Заточка инструмента.
Комплектация
- Плита распиловочная с вкладышем;
- ограничитель в сборе с ориентатором;
- ограждение пилы;
- кронштейны;
- угольник направляющий для распиловки;
- призма;
- труба;
- стол;
- плита приставная;
- угольник направляющий для фугования;
- шибер;
- винт;
- винт-барашек;
- ограждение вала;
- шайбы картонные;
- ограждение в сборе с пластинами;
- экран;
- втулки;
- болт с проточенным концом;
- стойка;
- болт со сферической головкой;
- струбцина;
- насадка-фреза;
- пила продольная диаметром 200 мм;
- резцы;
- болты;
- винты;
- гайки;
- шайбы;
- инструкция по эксплуатации.

Видео обзор
Деревообрабатывающий станок убдн-6м.+++Киев+++
Тема данной статьи – деревообрабатывающий станок убдн-6м.
Производится деревообрабатывающий станок убдн-6м в Молдавии. Данная модель станка пользуется огромной популярностью как на российском, украинском, так и белорусском рынке, имеет положительные отзывы от покупателей.
Компания «Электромотор» предлагает деревообрабатывающий станок убдн-6м по одной из самых приемлемых цен в Украине.
Деревообрабатывающий станок убдн-6м отличается компактными размерами, удобством пользования (возможен сбор опилок, а также работа от розеток, которые не имеют заземления). Данный станок можно использовать также как бытовое настольное устройство.
С помощью такого комбинированного станка Вы сможете выполнять следующие операции: токарную обработку, фуговать древесину, изготавливать для дверных и оконных проемов заготовки, делать распил под углом наклона, затачивать инструмент, выполнять поперечный и продольный распил брусьев. Также с помощью данного станка можно выполнять различные работы с пластмассой.
Также с помощью данного станка можно выполнять различные работы с пластмассой.
Деревообрабатывающий станок убдн-6м воплотит в жизнь все связанные с работой по дереву мечты. Он поможет оформить Вашу квартиру деревом, украсить дачный участок, сделать отделку балкона, одним словом, поможет создать уют в Вашем доме.
| {youtube: 500 350} |
Технические характеристики:
- Масса- 60 кг;
- Номинальная мощность- 1100 Вт.;
- Потребляемая мощность- 1500 Вт.;
- Толщина заготовки- 55 мм.;
- Длина заготовки- 420 мм.;
- Диаметр заготовок- 70 мм.;
- Обрабат. поверх. (шир.)- 200 мм;
- Толщина снимаемого слоя- от 0,2 до 3 мм.;
- Наибольшая глубина пропила- 55 мм.;
- Диаметр окружности резания- 76 мм.
 ;
; - Диаметр окружности резания- 200 мм.;
- Глубина выборки- 15 мм.;
- Диаметр хвостовика инструмента- 13 мм.;
- Окруж. раб. скор. шлиф. круга- 23 м/с;
- Част. вращ. фугова. Круга- 3500 об/мин.;
- Макс. диам. шлиф. круга- 125 мм.;
- Ширина ножа- 40 мм.;
- Напряжение- 220 В.;
- Режим работы- продолжительный;
- Страна-производитель- Молдавия;
- Гарантия- 1 год.
Рекомендуем ознакомиться:
Комбинированный фуговально-рейсмусовый станок Zenitech rfk 410. Оптовые цены! Купить в Киеве
Только в компании «Электромотор» Вы сможете приобрести инструмент, оборудование от лучших мировых производителей по самой доступной цене в Украине!
Доставку осуществляем по всей территории Украины.
Если Вы не уверены в своем выборе, либо же не нашли необходимую модель оборудования у нас на сайте, а также по вопросам оформления покупки звоните нам на тел. : – мы подберем агрегат соответствующий Вашим меркам!
: – мы подберем агрегат соответствующий Вашим меркам!
Купив у нас, Вы гарантировано останетесь довольными как качеством приобретенной продукции, так и ценой!
Для нас очень важно Ваше доверие и сотрудничество!
Наш адрес: г. Киев, просп. Лесной, 39 а.
Мы торгуемся, на все станки как деревообрабатывающие так и металлообрабатывающие есть промо коды на скидку. Не стесняйтесь – всегда спрашивайте про скидку. В Интернет магазине компании Электромотор скидка может составлять до 50%. Все станки и просто инструмент в нашем Интернет имеют гарантию от 1 года Мы предлагаем как бытовые так и мощные промышленные машины . Больше станков и для дома и для небольших производств Вы найдете в нашем магазине – https://elektromotor.com.ua/g46943952-tsirkulyarnye-pily На нашем сайте не только китайские модели, но и качественные мировые бренды ведущих мировых производителей. Промо код на скидку stanok2020 . Обязательно посетите наш Интернет магазин.
Running sport media | Releases Nike Shoes% PDF-1. 5
%
1 0 объект
>
эндобдж
2 0 obj
> поток
application / pdf
5
%
1 0 объект
>
эндобдж
2 0 obj
> поток
application / pdf
 ys6?>: ZԆ} h ا # 4 Mi @ L2 + Jo ߱ GK ~ I + hr} wK Lh5
р.
ys6?>: ZԆ} h ا # 4 Mi @ L2 + Jo ߱ GK ~ I + hr} wK Lh5
р.Модифицированная модель на основе Physarum для задачи распределения пользовательского трафика
Принятая рукописьМодифицированная модель, вдохновленная Physarum, для задачи распределения пользовательского равновесия Шуай Сю, Вэнь Цзян, Синьянг Дэн, Йехан Шоу PII: DOI: Ссылка:
S0307-904X (17) 30470-5 10.1016 / j.apm. 2017.07.032 APM 11882
Появится в:
Прикладное математическое моделирование
Дата получения: Дата пересмотра: Дата принятия:
19 декабря 2016 г. 3 июля 2017 г. 18 июля 2017 г.
Цитируйте эту статью как: Shuai Xu, Wen Цзян, Синьянг Дэн, Йехан Шоу, Модифицированная модель, вдохновленная Physarum, для задачи распределения пользовательского равновесия, Прикладное математическое моделирование (2017), DOI: 10.1016 / j.apm.2017.07.032
Это PDF-файл неотредактированной рукописи, принятой к публикации. В качестве услуги для наших клиентов мы предоставляем эту раннюю версию рукописи. Рукопись будет подвергнута копирайтингу, верстке и проверке полученного доказательства, прежде чем она будет опубликована в окончательной форме. Обратите внимание, что во время производственного процесса могут быть обнаружены ошибки, которые могут повлиять на содержание, и все юридические оговорки, относящиеся к журналу, имеют отношение.
Рукопись будет подвергнута копирайтингу, верстке и проверке полученного доказательства, прежде чем она будет опубликована в окончательной форме. Обратите внимание, что во время производственного процесса могут быть обнаружены ошибки, которые могут повлиять на содержание, и все юридические оговорки, относящиеся к журналу, имеют отношение.
ПРИНЯТО РУКОВОДСТВО
Основные моменты
CR IP T
• Предлагается модифицированная модель, вдохновленная Physarum, для задачи равновесия пользователя.• Учитываются характеристики двустороннего трафика и несколько пар OD.
AC
CE
PT
ED
M
AN US
• Предложенная модель, вдохновленная Physarum, очень эффективна как с точки зрения точности, так и с точки зрения времени выполнения
1
ACCEPTED MANUSCRIPT 9000 CR IP T
Модифицированная модель, вдохновленная Physarum, для задачи распределения пользовательского равновесия Шуай Сюа, Вэнь Цзянга, ∗, Синьянг Дэнга, Йехан Шоуа
Школа электроники и информации Северо-Западного политехнического университета, Сиань, Шаньси, 710072 , Китай
AN US
a
Реферат
PT
ED
M
Принцип распределения трафика пользовательского равновесия очень важен в задаче назначения трафика. Модели математического программирования предназначены для решения проблемы равновесия пользователя в традиционных алгоритмах. Недавно Physarum продемонстрировал способность решать проблемы пользовательского равновесия и оптимизации распределения трафика. Однако модель Physarum неэффективна в реальных сетях трафика с двухсторонними характеристиками трафика и несколькими парами исходный-целевой. В этой статье предлагается модифицированная модель, вдохновленная Physarum, для задачи пользовательского равновесия. Путем декомпозиции потока трафика на основе узлов происхождения поток трафика из разных пар отправка-место назначения может быть выделен в предлагаемой модели.Physarum может получить равновесный поток трафика, когда не может быть обнаружен более короткий путь между каждой парой происхождения-назначения. Наконец, численные примеры демонстрируют свойства рациональности и сходимости предложенной модели.
Модели математического программирования предназначены для решения проблемы равновесия пользователя в традиционных алгоритмах. Недавно Physarum продемонстрировал способность решать проблемы пользовательского равновесия и оптимизации распределения трафика. Однако модель Physarum неэффективна в реальных сетях трафика с двухсторонними характеристиками трафика и несколькими парами исходный-целевой. В этой статье предлагается модифицированная модель, вдохновленная Physarum, для задачи пользовательского равновесия. Путем декомпозиции потока трафика на основе узлов происхождения поток трафика из разных пар отправка-место назначения может быть выделен в предлагаемой модели.Physarum может получить равновесный поток трафика, когда не может быть обнаружен более короткий путь между каждой парой происхождения-назначения. Наконец, численные примеры демонстрируют свойства рациональности и сходимости предложенной модели.
AC
CE
Ключевые слова: Трафик, пользовательское равновесие, Physarum polycephalum, проблема распределения трафика
∗ Автор, ответственный за переписку: Школа электроники и информации Северо-Западного политехнического университета, Сиань, Шаньси, 710072, Китай. Тел .: +86029 88431267; факс: +86029 88431267. Адрес электронной почты: jiangw [электронная почта защищена], [электронная почта защищена]
Тел .: +86029 88431267; факс: +86029 88431267. Адрес электронной почты: jiangw [электронная почта защищена], [электронная почта защищена]
Препринт отправлен в Applied Mathematical Modeling
25 июля 2017 г.
ПРИНЯТО РУКОВОДСТВО
1. ВВЕДЕНИЕ
AN US
CR IP T
Назначение трафика относится к способу, с помощью которого заданная совокупная потребность в трафике пары исходный пункт (OD) назначается маршрутам трафика этой пары OD [1, 2, 3, 4, 5]. В качестве важной парадигмы назначения трафика пользовательское равновесие (UE) выбора пути путешественников в сетях трафика было впервые концептуализировано Уордропом [6].Принцип UE основан на предположении, что путешественник знает точную стоимость маршрута и выберет маршрут с минимальной стоимостью. Пользовательское равновесие достигается, когда все путешественники между одной и той же парой OD имеют одинаковую и минимальную стоимость [7, 8]. Кроме того, транспортные расходы любого путешественника не могут быть уменьшены за счет изменения маршрута в одностороннем порядке.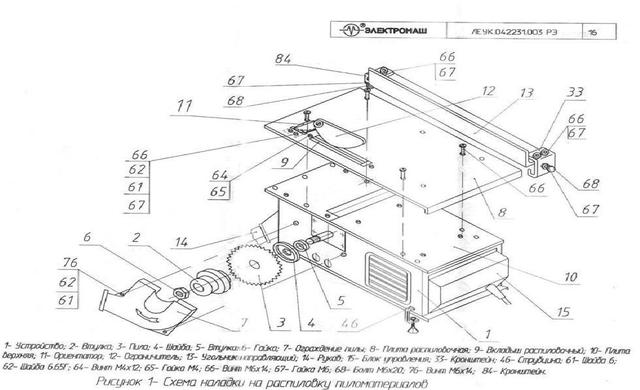
AC
CE
PT
ED
M
В существующей литературе многие алгоритмы были разработаны для решения проблемы UE [9, 10, 11], которые можно полностью разделить на три типа: на основе ссылок алгоритмы, алгоритмы на основе пути и алгоритмы на основе происхождения.Метод линейной аппроксимации Франк-Вульфа (FW) [12] был наиболее популярным на практике алгоритмом из-за своей простоты. В качестве метода линейной аппроксимации алгоритм FW имеет сублинейную асимптотическую скорость сходимости [9]. Как следствие, высокоточные решения не могут быть достигнуты за разумное время вычислений. Было предпринято множество попыток повысить эффективность алгоритма FW [13], т.е. алгоритма сопряженного Франка-Вульфа (CFW) и алгоритма двойного сопряжения Франка-Вульфа (BFW) [15].В алгоритмах, основанных на путях, проблема UE решается прямым достижением потока на путях [16]. Поток трафика назначается путем фиксации потока от других пар OD для каждой пары OD. В существующих алгоритмах, основанных на путях, широко используются алгоритм дезагрегированной симплициальной декомпозиции (DSD) [14] и алгоритм проекции градиента (GP) [17, 18, 9]. И DSD, и GP показали отличные результаты по сравнению с алгоритмом FW [19, 20], но требование памяти обычно считается непрактичным для крупномасштабных сетей.Алгоритм на основе происхождения, предложенный Бар-Гера [21, 22], не требует столько памяти, сколько алгоритмы на основе путей. Алгоритм вычисляет последовательно для каждой исходной подсети с использованием квазиньютоновского подхода. Позже Диал [23] разработал другой алгоритм, основанный на происхождении, путем последовательного смещения потоков от самого длинного пути к самому короткому. Хотя алгоритмы на основе источника могут обеспечивать как потоки трафика каналов, так и потоки трафика маршрутов [24], перечисление всех потоков маршрутов каждой подсети довольно сложно.3
И DSD, и GP показали отличные результаты по сравнению с алгоритмом FW [19, 20], но требование памяти обычно считается непрактичным для крупномасштабных сетей.Алгоритм на основе происхождения, предложенный Бар-Гера [21, 22], не требует столько памяти, сколько алгоритмы на основе путей. Алгоритм вычисляет последовательно для каждой исходной подсети с использованием квазиньютоновского подхода. Позже Диал [23] разработал другой алгоритм, основанный на происхождении, путем последовательного смещения потоков от самого длинного пути к самому короткому. Хотя алгоритмы на основе источника могут обеспечивать как потоки трафика каналов, так и потоки трафика маршрутов [24], перечисление всех потоков маршрутов каждой подсети довольно сложно.3
ПРИНЯТОЕ РУКОВОДСТВО
PT
ED
M
AN US
CR IP T
Биологические системы обычно вдохновляют компьютерных ученых и инженеров обрабатывать информацию и принимать решения. К настоящему времени были предложены некоторые эвристические алгоритмы для решения проблемы распределения трафика, такие как алгоритм муравьиной колонии [25, 26] и генетический алгоритм [27]. В последнее время слизевик Physarum polycephalum становится популярным живым компьютерным субстратом [28, 29].Машины Physarum оказались наиболее успешными биологическими субстратами при решении задач вычислительной геометрии, оптимизации и логики, поскольку их легко реализовать [30]. В этой статье предлагается модифицированная модель, вдохновленная Physarum, для решения проблемы распределения трафика UE. Physarum polycephalum – крупный амебоидный организм, содержащий большое количество ядер и протоплазматических трубок [31]. Эти протоплазматические трубки будут распределять протоплазму в виде сетей цитоскелета. Эксперимент показал, что Physarum способен находить короткий путь между двумя точками в заданном лабиринте [32].Математическая модель может отражать базовую динамику адаптируемости сети посредством итераций локальных правил и дает решения со свойствами, сопоставимыми или лучшими, чем у реальных инфраструктурных сетей [33]. Сходимость Physarum в поиске кратчайшего пути была доказана Bonifaci et al.
В последнее время слизевик Physarum polycephalum становится популярным живым компьютерным субстратом [28, 29].Машины Physarum оказались наиболее успешными биологическими субстратами при решении задач вычислительной геометрии, оптимизации и логики, поскольку их легко реализовать [30]. В этой статье предлагается модифицированная модель, вдохновленная Physarum, для решения проблемы распределения трафика UE. Physarum polycephalum – крупный амебоидный организм, содержащий большое количество ядер и протоплазматических трубок [31]. Эти протоплазматические трубки будут распределять протоплазму в виде сетей цитоскелета. Эксперимент показал, что Physarum способен находить короткий путь между двумя точками в заданном лабиринте [32].Математическая модель может отражать базовую динамику адаптируемости сети посредством итераций локальных правил и дает решения со свойствами, сопоставимыми или лучшими, чем у реальных инфраструктурных сетей [33]. Сходимость Physarum в поиске кратчайшего пути была доказана Bonifaci et al. [34]. Основываясь на своем поведении в поисках пищи, Physarum до сих пор использовался для решения многих задач, таких как поиск кратчайшего пути в направленной или ненаправленной сети [35, 36, 37, 38], проектирование и моделирование транспортной сети [39, 40, 41 , 42], естественная реализация пространственной логики [43, 44] и компьютерная музыка [45, 46, 47].Кроме того, модель Physarum может также найти кратчайший путь в неопределенной среде [48, 49] в реальном приложении [50].
[34]. Основываясь на своем поведении в поисках пищи, Physarum до сих пор использовался для решения многих задач, таких как поиск кратчайшего пути в направленной или ненаправленной сети [35, 36, 37, 38], проектирование и моделирование транспортной сети [39, 40, 41 , 42], естественная реализация пространственной логики [43, 44] и компьютерная музыка [45, 46, 47].Кроме того, модель Physarum может также найти кратчайший путь в неопределенной среде [48, 49] в реальном приложении [50].
AC
CE
В последнее время довольно много исследователей пытаются применить модель Physarum для решения проблемы распределения трафика [51, 52]. Эти модели, вдохновленные Physarum, могут хорошо влиять в определенных условиях, когда сети подключаются в одностороннем порядке. Но существующие модели не могут быть реализованы в сетях трафика с двусторонними характеристиками трафика.Модель Physarum для проблемы назначения трафика UE [52] не может отличить поток от разных пар OD, что означает, что модель нецелесообразна в сетях трафика с несколькими парами OD. В этой статье предлагается модифицированная модель, вдохновленная Physarum, для задачи распределения трафика UE для сетей трафика с характеристиками двустороннего трафика. В предлагаемой модели потоки декомпозируются по узлам происхождения как алгоритмы, основанные на происхождении. Для каждой подсети потоки назначаются моделью Physarum
В этой статье предлагается модифицированная модель, вдохновленная Physarum, для задачи распределения трафика UE для сетей трафика с характеристиками двустороннего трафика. В предлагаемой модели потоки декомпозируются по узлам происхождения как алгоритмы, основанные на происхождении. Для каждой подсети потоки назначаются моделью Physarum
4
ACCEPTED MANUSCRIPT
на основе ее протоплазменной сетевой адаптивности и непрерывности.
AN US
CR IP T
Структура этого документа следующая. В разделе 2 рассматривается принцип распределения пользовательского равновесного трафика. Кратко представлены исходная модель Physarum polycephalum и вдохновленная Physarum модель для задачи распределения трафика UE, предложенная Чжаном [52]. В разделе 3 представлена модифицированная модель Physaruminspired для задачи распределения трафика UE. В разделе 4 приведены численные примеры, демонстрирующие свойства рациональности и сходимости предложенной модели.Наконец, статья заканчивается выводами и предложениями для дальнейших исследований в Разделе 5.
2. ПРЕДВАРИТЕЛЬНАЯ ИНФОРМАЦИЯ
M
В этом разделе кратко представлены некоторые предварительные сведения, включая модель распределения трафика [7], исходную модель Physarum polycephalum. [53] и вдохновленная Physarum модель проблемы UE, предложенная Чжаном [52].
ЭД
2.1. Модель назначения трафика для равновесия пользователей
CE
PT
Транспортная сеть – это сильно связанный ориентированный граф G (N, A), где N – набор узлов, а A – набор направленных связей.Предположим, что нет никаких ссылок от узла к самому себе и только одна ссылка, если таковая имеется, между двумя разными узлами. Предположим, что R и S обозначают набор исходных узлов и набор конечных узлов, а r ∈ R, s ∈ S, R, S j N. Пусть Krs и qrs обозначают множество всех путей и потребность в перемещении между OD-парой r – s, тогда мы имеем: X fkrs = qrs, ∀r ∈ R, s ∈ S (1) k∈Krs
fkrs
AC
где – поток трафика на пути k между парой OD r – s. Пусть xa обозначает поток трафика по ссылке a. Тогда все узлы, кроме узлов источника и узлов назначения, удовлетворяют закону сохранения потока [52], который показан следующим образом: XX xa = xb, ∀j, k ∈ N \ {R, S} (2) a≡ [(i, j) ∈A]
Тогда все узлы, кроме узлов источника и узлов назначения, удовлетворяют закону сохранения потока [52], который показан следующим образом: XX xa = xb, ∀j, k ∈ N \ {R, S} (2) a≡ [(i, j) ∈A]
b≡ [(j, k) ∈A]
5
ПРИНЯТАЯ РУКОВОДСТВО
∂ta (xa) = 0, ∂tb
∀a ∈ A
(3)
(4)
AN US
∂ta (xa)> 0, ∂xa
∀a, b ∈ A
CR IP T
Пусть ta (xa) обозначает время трафика, которое испытывает каждый пользователь в канале. a, когда xa единиц техники движутся по звену.ta (.) – это монотонно неубывающая и непрерывно дифференцируемая функция времени трафика для потока на линии а из-за влияния перегрузки на время в пути [7], которая может быть выражена следующим образом:
a
XXX
ED
xa =
M
Пусть Krs обозначает набор маршрутов между парой OD r −s и. Пусть crs k представляет время трафика на пути k между парой OD r – s, k ∈ Krs и rs δa, k обозначает коэффициент корреляции между каналом трафика и трактом трафика, rs δa, k = 1, если k-й путь между OD пара r – s пересекает звено a, иначе rs δa, k = 0. Время трафика пути crs k и поток трафика канала xa могут быть выражены как [7]: X rs ta · δa, k, ∀r ∈ R, s ∈ S, k ∈ Krs (5) crs k = r
Время трафика пути crs k и поток трафика канала xa могут быть выражены как [7]: X rs ta · δa, k, ∀r ∈ R, s ∈ S, k ∈ Krs (5) crs k = r
s
k
rs fkrs · δa, k,
∀a ∈ A
(6)
AC
CE
PT
Принцип равновесия пользователей Wardrop [6] заключается в том, что путешественники стремятся минимизировать связанные с этим расходы. с выбранными ими маршрутами. Предполагается, что путешественники имеют точную информацию о реальных условиях путешествия, и они могут быть идентичными в том смысле, что они одинаково оценивают время, денежные затраты и другие атрибуты маршрута.Пользовательское равновесие Wardrop достигается, когда время движения путешественников не может быть сокращено путем одностороннего изменения маршрутов, что может быть выражено следующим образом: = 0, fkrs> 0 rs urs – ck, ∀r ∈ R, s ∈ S, k ∈ Krs ( 7) ≤ 0, fkrs = 0, где urs – наименьшее время трафика между парой OD r – s при равновесии трафика.
6
ПРИНЯТОЕ РУКОВОДСТВО
При сделанных выше предположениях задача распределения трафика может быть математически сформулирована как следующая задача выпуклой оптимизации [7]: PR xa ta (w) dw min Z (x) = 0 xa = P
[(i, j) ∈A]
P
k fkrs
PPP
rs, fkrs · δa, krs kP xa = xb, [(j, k) ∈A]
fkrs = qrs,
∀j, k ∈ N \ {R, S}
(8)
∀r ∈ R, s ∈ R
∀r ∈ R, s ∈ R, k ∈ Krs ∀a ∈ A
AN US
≥ 0, xa ≥ 0,
∀a ∈ A
CR IP T
a
s. т.
т.
2.2. Происхождение Physarum Polycephalum Модель
ED
M
Physarum polycephalum – одноклеточный амебоидный организм, который также называется плазмодием в вегетативной фазе [53]. Он обладает способностью решать выбор кратчайшего пути, основанный на его особом механизме поиска пищи: трансформации протоплазматических трубок и положительной обратной связи от скорости потока. Высокая скорость потока заставляет трубки утолщаться, и диаметр трубки уменьшается при низкой скорости потока [53].Ниже приводится полное введение в модель поиска пути Physarum polycephalum.
AC
CE
PT
Предположим, что форма сети, образованной Physarum, представлена графом G (N, A), где край графа обозначает плазмодиальную трубку, а узел обозначает соединение между трубки. И N – это набор узлов, где N1 и N2 подписаны как исходный и целевой узлы, любые другие помечены как N3, N4, N5 и т. Д. Граничный соединяющий узел i и узел j отмечен как Mij, а поток от узел Ni к узлу Nj через ребро Mij обозначается как Qij, как показано [53]: Qij =
πr4ij Dij (pi – pj) = (pi – pj) 8ηLij Lij
(9)
, где η – вязкость жидкости, а Dij = πr4ij / 8η – мера проводимости краевой трубы Mij. А pi – мера давления в узле ni, Lij – длина ребра Mij. Согласно закону течения 7
А pi – мера давления в узле ni, Lij – длина ребра Mij. Согласно закону течения 7
ПРИНЯТОЙ РУКОВОДСТВО
приток и отток должны быть сбалансированы, а именно: X Qij = 0, (j 6 = 1, 2)
(10)
i
X i
Qi2 – I0 = 0
CR IP T
, особенно для исходных узлов N1 и N2, уравнения потока могут быть выражены как: X Qi1 + I0 = 0 (11) (12)
AN US
где I0 – это поток от исходного узла к конечному узлу, который в модели считается постоянным.Согласно уравнениям (9-12) сетевое уравнение Пуассона для давления выводится следующим образом: f или j = 1, −1 X Dij +1 f или j = 2, (pi – pj) = ( 13) Lij i 0 в противном случае
M
путем дальнейшей установки p2 = 0 в качестве базового уровня давления, давление всех узлов может быть определено, давление всех узлов может быть определено в соответствии с уравнением (13) и все Qij можно определить, решив уравнение (9).
AC
CE
PT
ED
Предполагается, что для адаптации к адаптивному поведению плазмодия проводимость Dij изменяется при адаптации к потоку Qij. А трубки с нулевой проводимостью вымрут. Проводимость каждой трубки описывается следующим образом: [33]: d Dij = f (| Qij |) – αDij (14) dt где α – скорость распада трубки, а f (.) – монотонно возрастающая непрерывная функция, удовлетворяющая f (0) = 0. 2.3. Модель на основе Physarum для проблемы UE
А трубки с нулевой проводимостью вымрут. Проводимость каждой трубки описывается следующим образом: [33]: d Dij = f (| Qij |) – αDij (14) dt где α – скорость распада трубки, а f (.) – монотонно возрастающая непрерывная функция, удовлетворяющая f (0) = 0. 2.3. Модель на основе Physarum для проблемы UE
В соответствии с особенностями системы кормового поведения Physarum проблема оптимума и проблема равновесия пользователя в сетях с направленным движением решаются с помощью модифицированных моделей Physarum [51, 52].Модель Physarum для проблемы УЭ в [52] отличается от оригинальной модели Physarum в двух пунктах. 8
CR IP T
ПРИНЯТО РУКОВОДСТВО
(a) Исходная модель
(b) Модель, модифицированная Чжаном [52]
Рисунок 1: Простые сети для модели Physarum
AN US
Во-первых, Исходная модель Physarum может найти только кратчайший путь в неориентированных сетях, показанных на рисунке 1 (а). Модифицированный метод был предложен для распространения исходной модели Physarum на направленные сети. Общее введение для модифицированной модели дано ниже.
Общее введение для модифицированной модели дано ниже.
ED
M
В модифицированной модели каждая кромка рассматривается как две трубы с противоположными направлениями и одинаковым весом, что показано на рисунке 1 (b). И есть только одно направление между двумя узлами в сети, что означает, что поток может течь только от узла s к узлу 1 и не может течь в противоположном направлении, как показано на рисунке 1 (b). А сетевое уравнение Поссона, определенное в уравнении (13), было модифицировано следующим образом [52]: f или j = 1, −1 X Dij Dji +1 f или j = 2, (+) + (pi – pj) = (15) LL ij ji i 0 в противном случае
CE
PT
где Lij обозначает время пути от узла i к узлу j, а Lji обозначает время пути от узла j к узлу i.Точно так же Dij и Dji имеют разные значения. При инициализации, если Lij = inf, тогда Dij = 0. В противном случае присвойте Dij значение от 0 до 1. Чтобы гарантировать несогласованность, Qij следует сохранять 0 во время итераций, если Lij = inf.
AC
Во-вторых, в сетях только один источник и один пункт назначения. Однако обычно в транспортных сетях имеется несколько пар OD. Для управления сетью с несколькими исходными и конечными точками уравнение (15) было изменено следующим образом [52]: ∀r ∈ R, −Ir, X Dij Dji + Is, ∀s ∈ s, +) (pi – pj ) = (16) ( LL ij ji i 0, в противном случае 9
ПРИНЯТО РУКОВОДСТВО
CR IP T
где r обозначает исходный узел, а r ∈ R, s обозначает узел назначения, а s ∈ S.Ir и Is представляют собой единицы потока, поставляемые исходным узлом r и потребляемые конечным узлом s, соответственно.
3. ПРЕДЛАГАЕМЫЙ МЕТОД
AN US
В этом разделе мы обсудим недостатки оригинального метода, вдохновленного Physarum, для задачи UE [52] и предложим модифицированный метод Physaruminspired для решения проблемы UE. 3.1. Недостатки метода, основанного на методе Origin Physarum
M
По сравнению с предыдущими моделями слизистой плесени, метод решения проблемы UE, вдохновленный Physarum, лучше подходит для характеристики его кормодобывающей активности. Однако обнаружены два недостатка оригинального метода решения проблемы UE, основанного на Physarum, а именно:
Однако обнаружены два недостатка оригинального метода решения проблемы UE, основанного на Physarum, а именно:
AC
CE
PT
ED
1. Обратите внимание, что между двумя узлами в показанной сети есть только одно направление. на рисунке 1 (b), что означает, что поток может течь только от одного узла к другому, но никогда в противоположном направлении. Однако в реальных транспортных сетях большинство дорог имеют характеристики двустороннего движения, как показано на рисунке 2. Очевидно, что противоположные направления разделены друг с другом, и потоки не пересекаются в двух противоположных направлениях.Очевидно, что оригинальный метод, вдохновленный Physarum, не может быть реализован в сети трафика, показанной на рисунке 2.
Рисунок 2: Реальная сеть трафика
10
ПРИНЯТО РУКОВОДСТВО
Маленькая сеть с несколькими источниками и несколькими приемниками
AN US
Пример
CR IP T
2. Модель проблемы UE, основанная на Physarum, нецелесообразна в сетях трафика с несколькими парами OD. Модифицированное уравнение (16) удовлетворяет только закону сохранения потока в транспортной сети.Однако он не может различить поток в каждой паре OD, что означает, что для данной пары OD r – s выходной поток в узле s не равен входному потоку в узле r. Фактически, вдохновленная Physarum модель проблемы UE подходит только для сетей трафика с одним источником и несколькими приемниками или несколькими источниками и одним приемником. Здесь мы проиллюстрируем эту проблему на следующем примере.
Модифицированное уравнение (16) удовлетворяет только закону сохранения потока в транспортной сети.Однако он не может различить поток в каждой паре OD, что означает, что для данной пары OD r – s выходной поток в узле s не равен входному потоку в узле r. Фактически, вдохновленная Physarum модель проблемы UE подходит только для сетей трафика с одним источником и несколькими приемниками или несколькими источниками и одним приемником. Здесь мы проиллюстрируем эту проблему на следующем примере.
AC
CE
PT
ED
M
Здесь мы используем небольшую сеть трафика с 4 узлами, 4 связями и 2 парами OD, которые показаны на рисунке 3.А потребности отправления-назначения в транспортных средствах в час составляют q1,2 = 100 и q4,3 = 100. Для простоты время в пути рассчитывается функцией Бюро дорог общего пользования США (BPR) [54], которая выражается следующим образом: Qa ta = αa (1 + 0,15 () 4) (17) ca, где ta, αa, Qa, ca обозначают время в пути, время свободного потока, транспортный поток и пропускную способность на линии а, соответственно.
Рисунок 3: Небольшая сеть трафика
При использовании модели, вдохновленной Physarum, потоки путей показаны в таблице 1.Понятно, что распределение трафика не удовлетворяет потребности трафика, поток по пути 1 → 3 и пути 4 → 2 должен быть равен 100. Обратите внимание, что время прохождения свободного потока для 1 → 3 и 4 → 2 намного меньше, чем это из 1 → 2 11
ПРИНЯТОЕ РУКОВОДСТВО
и 4 → 3. Очевидно, что модель не различает поток от разных пар наружных диаметров. В результате модель, вдохновленная Физарумом, назначает больший поток путям 1 → 3 и 4 → 2. Путь (последовательность узлов)
Поток пути
→ → → →
19.5177 80.4823 80.4823 19.5177
2 3 2 3
Стоимость пути 10.0348 10.0348 10.0348 10.0348
AN US
1 1 4 4
CR IP T
Таблица 1: Потоки маршрутов сети трафика
, показанные на рисунке 3 9000 3.2. Модифицированная модель на основе Physarum для проблемы UEM
Здесь мы предлагаем модифицированную модель на основе Physarum для проблемы UE, чтобы преодолеть эти вышеупомянутые недостатки. 3.2.1. Модифицированная модель Physarum для кратчайшего пути в направленных сетях
3.2.1. Модифицированная модель Physarum для кратчайшего пути в направленных сетях
CE
PT
ED
Для удовлетворения характеристик реальной сети трафика, показанной на рисунке 2, каждое ребро рассматривается как две трубы с противоположными направлениями и разным весом.И поток может течь в противоположных направлениях, не мешая друг другу. Уравнение сети Posson такое же, как уравнение (15). Но для сохранения справедливости проводимости уравнение проводимости, определенное в уравнении (9), должно быть улучшено следующим образом: (Dij Dij (pi – pj), (pi – pj)> 0 L Lij ij (18) Qij = 0, в противном случае
AC
, когда поток в каждой трубке отрицательный, потоку будет присвоено значение 0. Это потому, что поток не может пройти через данную трубку в противоположном направлении.При инициализации, если Lij 6 = inf, мы присваиваем Dij значение от 0 до 1. В противном случае проводимость Dij присваивается 0. В частности, когда Lij = inf или Lji = inf, что означает, что поток может течь только от узла j к узлу i или от узла i к узлу j, наша модифицированная модель 12
ПРИНЯТО РУКОВОДСТВО
– то же самое, что введено в разд. 2.3. Собственно, модель, представленная в гл. 2.3 – это частный случай нашей модифицированной модели.
2.3. Собственно, модель, представленная в гл. 2.3 – это частный случай нашей модифицированной модели.
n + 1 n Dij – Dij n + 1 = Qnij – Dij δt
CR IP T
Как указано в [53], Physarum всегда может сходиться к кратчайшему пути, когда f (| Qij |) = | Qij | и α = 1.Из уравнения (18) следует, что Qij ≥ 0, поэтому проводимость каждой трубки в уравнении (14) можно обновить следующим образом:
(19)
AN US
3.2.2. Модифицированная модель Physarum для направленных сетей с источниками и несколькими стоками
M
Чтобы преодолеть недостаток, заключающийся в том, что модель, вдохновленная Physarum, не может различать поток в каждой паре OD, мы модифицируем модель, вдохновленную Physarum, как показано ниже. Пусть Sr обозначает набор узлов назначения, которые происходят из узла r. Ясно, что мы имеем: X Irs (20) Ir = s∈Sr
AC
CE
PT
ED
, где Ir обозначает входной поток в исходном узле r, а Irs означает выходной поток в целевом узле. s происходит из узла r.Здесь мы рассматриваем сеть с несколькими источниками и несколькими приемниками как суперпозицию сетей с одним источником и несколькими сетями приемников. Для каждой сети с одним источником и несколькими стоками мы модифицируем исходное сетевое уравнение Пуассона (13) следующим образом: P – Irs, f или j = r, X Dij Dji s∈Srs (21) +) (pi – pj) = (+ Irs, ∀s ∈ Srs, Lij Lji i 0, иначе, естественно, поток каждой трубки во всех подсетях может быть вычислен по формуле (18). Согласно принципу суперпозиции, поток каждую трубку в исходной сети множественных источников и стоков можно выразить следующим образом: X Qall = Qrij, ∀i, j ∈ N (22) ij r∈R
s происходит из узла r.Здесь мы рассматриваем сеть с несколькими источниками и несколькими приемниками как суперпозицию сетей с одним источником и несколькими сетями приемников. Для каждой сети с одним источником и несколькими стоками мы модифицируем исходное сетевое уравнение Пуассона (13) следующим образом: P – Irs, f или j = r, X Dij Dji s∈Srs (21) +) (pi – pj) = (+ Irs, ∀s ∈ Srs, Lij Lji i 0, иначе, естественно, поток каждой трубки во всех подсетях может быть вычислен по формуле (18). Согласно принципу суперпозиции, поток каждую трубку в исходной сети множественных источников и стоков можно выразить следующим образом: X Qall = Qrij, ∀i, j ∈ N (22) ij r∈R
13
ПРИНЯТО РУКОВОДСТВО
3.2.3. Модифицированная модель Physarum для проблемы UE
CR IP T
, где Qall ij обозначает поток от узла i к узлу j в исходной сети с несколькими источниками и несколькими приемниками, а Qrij представляет поток от узла i к узлу j в подсети, исходящей из узел r.
Lan + 1 =
AN US
Обратите внимание, что в процессе приближения Phyasrun к кратчайшему пути поток и проводимость вдоль каждого звена являются непрерывными. Продолжая рассматривать непрерывность и динамическую реконфигурацию модели Physarum, мы можем обновлять время прохождения ссылки в каждой итерации.Поток будет перераспределен модифицированной моделью Physarum, когда время прохождения канала будет обновлено во время итераций. Длина звена a обновляется следующим образом: n + 1 Lna + ta (Qall) a 2
(23)
ED
M
n + 1, где Qall обозначает общий поток на канале a в (n + 1) -я итерация, Lna a и Ln + 1 представляют длину звена a на n-й и (n + 1) -й итерации. a n + 1 И направление поиска длины связи La руководствуется ta (Qall). Обратите внимание, что все в равновесии, будет La = ta (Qa), что означает, что длина звена а равна времени прохождения по звену а.
PT
Здесь основные шаги модифицированной модели на основе Physarum для задачи равновесия пользователей представлены в алгоритме 1.
CE
3.3. Обсуждение
AC
В этом подразделе было доказано, что распределение потока, полученное из предложенной модели, вдохновленной Physarum, удовлетворяет принципу UE. Критерии остановки предлагаемого алгоритма также обсуждаются ниже. 3.3.1. Поток Physarum удовлетворяет принципу UE
Лемма 1.Когда предложенный алгоритм, вдохновленный Физарумом, сходится, длина любого звена La равна времени в пути ta (Qall a). 14
CR IP T
ПРИНЯТО РУКОВОДСТВО
Алгоритм 1 Модифицированная модель на основе Physarum для проблемы UE
CE
PT
ED
M
AN US
// Матрица Qr является потоком происходит из узла r. // L0 – матрица времени пробега свободного потока. r Dij = [0.5, 1] (∀i, j = 1, 2, · · ·, N ∧ Cij0 6 = 0, ∀r ∈ R), если Cij0 == inf, то r = 0 Dij end, если Qrij = 0 ( ∀i, j = 1, 2, · · ·, N, ∀r ∈ R) 1 Qall ij = 0 (∀i, j = 1, 2, · · ·, N) 1 Lij = L0ij (∀i, j = 1, 2, · · ·, N) n = 1 // Счетчик итераций, пока N otConvergence do для r ∈ R do // Рассчитайте давление каждого узла, используя уравнение. (21) −Ir, f или j = r, r P Dijr Dji + I, ∀s ∈ Srs, (Lij + Lji) (pi – pj) = rs i 0, иначе // Вычислить поток каждого ребра используя уравнение (18) (rr Dij Dij (pi – pj), (pi – pj)> 0 Lij Lij Qrij = 0, иначе rrr Dij = (Dij + Qij) / 2, ∀i, j ∈ N end для P все Qij n + 1 = Qrij, ∀i, j ∈ N r∈R
(21) −Ir, f или j = r, r P Dijr Dji + I, ∀s ∈ Srs, (Lij + Lji) (pi – pj) = rs i 0, иначе // Вычислить поток каждого ребра используя уравнение (18) (rr Dij Dij (pi – pj), (pi – pj)> 0 Lij Lij Qrij = 0, иначе rrr Dij = (Dij + Qij) / 2, ∀i, j ∈ N end для P все Qij n + 1 = Qrij, ∀i, j ∈ N r∈R
alln + 1
Ln ij + ta (Qij 2
)
AC
Ln + 1 = ij n = n + 1 конец в то время как
15
ПРИНЯТАЯ РУКОВОДСТВО
Lij =
pi – pj, если pi> pj inf, в противном случае
CR IP T
n + 1 h Доказательство: Согласно Ref.[34], считается, что Dij = Dij, когда алгоритм, вдохновленный Physarumn, сходится. Подставляя его в уравнение (19), получаем Dij = n Qij при n = inf. Согласно уравнению (18), мы имеем
AN US
, что означает, что поток может только от узла высокого давления к узлу низкого давления. Давление каждого узла однозначно определяет давление узла. Другими словами, давление каждого узла является постоянным, поэтому мы имеем Ln + 1 = Lnij, когда n = inf. Подставляя его в уравнение (23), получаем, что ij all Ln + 1 = Qij n + 1 при n = inf.ij Лемма 2. Когда предложенный алгоритм, вдохновленный Physarum, сходится, путешественники между одной и той же парой OD имеют одинаковое и минимальное время в пути.
Подставляя его в уравнение (23), получаем, что ij all Ln + 1 = Qij n + 1 при n = inf.ij Лемма 2. Когда предложенный алгоритм, вдохновленный Physarum, сходится, путешественники между одной и той же парой OD имеют одинаковое и минимальное время в пути.
ED
M
Подтверждение: Согласно Ref. [34, 53], модель Physarum всегда может сходиться к кратчайшему пути, а проводимость вдоль звеньев вне кратчайшего n = Qnij, когда пути сходятся к нулям. Из леммы 1 следует, что Dij n = inf. Таким образом, поток вдоль звеньев за пределами кратчайшего пути сходится к нулям, что означает, что на путях с большим временем прохождения нет путешественника, чем у кратчайших путей, и все путешественники выбирают кратчайшие пути.
AC
CE
PT
Из леммы 1 и 2 следует, что поток Physarum удовлетворяет принципу UE. Сходимость Physarum в нахождении кратчайшего пути доказана в [5]. [34]. Но предлагаемый Physarum отличается от исходной модели Physarum из-за длины динамического звена (время прохождения звена). В настоящее время мы не доказали сходимость предложенной модели, вдохновленной Physarum. Однако следующие численные примеры демонстрируют свойства сходимости предложенной модели.3.3.2. Меры сходимости предложенного алгоритма Обычно существуют три меры сходимости для распределения трафика [22, 55], которые кратко представлены следующим образом:
В настоящее время мы не доказали сходимость предложенной модели, вдохновленной Physarum. Однако следующие численные примеры демонстрируют свойства сходимости предложенной модели.3.3.2. Меры сходимости предложенного алгоритма Обычно существуют три меры сходимости для распределения трафика [22, 55], которые кратко представлены следующим образом:
16
ПРИНЯТО РУКОВОДСТВО
все
n | Qij n + 1 – Qall ij | ≤ ε,
CR IP T
Принцип 1: В соответствии с ошибкой потоков трафика или временем прохождения, рассчитанным в двух смежных временах, решить, остановится ли итерация [12]. Вычисления остановятся только тогда, когда потоки станут стабильными в двух соседних итерациях.Эта простая и обычно эффективная мера позволяет получить потоки, удовлетворяющие принципу UE. Естественно, принцип сходимости можно выразить следующим образом: ∀i, j ∈ N
(24)
AN US
Принцип также может быть выражен как относительная погрешность каждого звена [25]: все n | Qij n +1 – Калл идж | ≤ ε, ∀i, j ∈ N (25) n Qall ij
RG =
Общее время пробега
(26)
PT
ED
M
Принцип 2: Согласно ошибке между время прохождения сети на основе путей и каналов, относительный промежуток (RG) и нормализованный промежуток (или избыточная средняя стоимость) принимаются во внимание для измерения сходимости [9]. Для данной итерации разрыв определяется как разница между общим временем в пути транспортного средства и стоимостью проезда транспортного средства, заданной назначением «все или ничего» (AON) на текущей итерации (равняется сумме требований OD, умноженных на стоимость кратчайший путь, соединяющий пару OD). RG определяется как отношение промежутка к общему времени в пути транспортного средства [56]. Показатель RG может быть выражен как:
Для данной итерации разрыв определяется как разница между общим временем в пути транспортного средства и стоимостью проезда транспортного средства, заданной назначением «все или ничего» (AON) на текущей итерации (равняется сумме требований OD, умноженных на стоимость кратчайший путь, соединяющий пару OD). RG определяется как отношение промежутка к общему времени в пути транспортного средства [56]. Показатель RG может быть выражен как:
AC
CE
Принцип 3: Ошибка между максимальным временем прохождения пути и минимальным временем прохождения пути между парой OD также является оценочным индексом сходимости [22]: rs rs rs rs εrs = max {crs k | k ∈ K, fk> 0} – min {ck | k ∈ K}
(27)
путем присвоения подходящего значения εrs, принцип UE может быть заархивирован.
Обычно Принцип 1 используется в методе на основе канала, таком как метод FW. Принцип 2 обычно используется в методе на основе пути, а Принцип 3 обычно используется в алгоритме на основе происхождения. Обратите внимание, что модифицированная модель Physaruminspired для проблемы UE фактически основана на времени прохождения линии связи. 17
Обратите внимание, что модифицированная модель Physaruminspired для проблемы UE фактически основана на времени прохождения линии связи. 17
ПРИНЯТО РУКОВОДСТВО
Во время итераций кратчайшие пути перемещения и максимальное время перемещения не доступны. Без дополнительных вычислительных затрат Принцип 1 можно принять в качестве критерия остановки:
i, j∈N
n | Qij n + 1 – Qall ij | n Qall ij
CR IP T
все
REQ = max
≤ε
(28)
M
AN US
Чтобы сократить время вычислений, для Принципа 2 можно заменить GP следующим образом [15]: U BDn – LBD RETn = ≤ε (29) LBD где U BDn и LBD обозначают текущую верхнюю и известную нижнюю границу общего времени в пути транспортного средства, соответственно.Нижняя граница LBD получается из других методов гораздо большим количеством итераций, чем общее условие. Однако стоимость вычислений LBD очень высока в некоторых сетях трафика. Итак, чтобы избежать вычисления LBD, LBD можно заменить на U BDn-1. Тогда имеем: U BDn – U BDn − 1 ≤ε (30) RELn = U BDn − 1
Тогда имеем: U BDn – U BDn − 1 ≤ε (30) RELn = U BDn − 1
ED
, где U BDn − 1 обозначает последний верхний предел общего времени в пути транспортного средства. . (28), уравнение (29) и уравнение (30), обозначаются как cr.1, cr.2 и cr.3 соответственно.Эти три критерия будут проверены на следующих числовых примерах.
AC
CE
PT
В предложенном алгоритме, вдохновленном Physarum, решение линейной системы уравнений необходимо для каждой подсети на основе источника. Обратите внимание, что было достигнуто много результатов в отношении параллельной модели Physarum [57], ясно, что параллельные вычисления могут быть реализованы для каждой подсети на основе источника. Кроме того, линейная система уравнений для каждой подсети, основанной на происхождении, очень специфична и может быть сформулирована как лапласова система, которая разрешима за O (m log n) шагов по времени [58].Для простоты параллельные вычисления не реализованы, и линейная система уравнений для каждой подсети на основе источника решается общим методом с O (n3) шагами по времени.
18
ПРИНЯТАЯ РУКОВОДСТВО
4. ЧИСЛЕННЫЕ ПРИМЕРЫ
CR IP T
В этом разделе проиллюстрированы числовые примеры, демонстрирующие свойства рациональности и сходимости модифицированного метода. Производительность предложенного алгоритма сравнивается с характеристиками FW, BFW и CFW.Далее рассматриваются три критерия cr.1, cr.2 и cr.3. Приведенные ниже вычислительные примеры используют Matlab на процессоре Intel (R) Core (TM) i5-5200U (2,2 ГГц) с 8,00 ГБ ОЗУ под Windows 8.
AN US
4.1. Пример 1
Здесь мы используем простую сеть, показанную на рисунке 3, и требования OD такие же, как и в разд. 3.1. При использовании модифицированной модели, вдохновленной Physarum, потоки путей показаны в таблице 2. Ясно, что модифицированная модель, вдохновленная Physarum, способна различать потоки в разных парах OD.
M
Таблица 2: Потоки пути, полученные в результате модифицированного метода
Путь (последовательность узлов)
Поток пути
Итерация
0,01
1 → 2 4 → 3
100100
17
PT
ED
критерий остановки (ε0)
CE
4. 2. Пример 2
2. Пример 2
AC
Чтобы проверить производительность предложенной модели, вдохновленной Physarum, мы провели ряд тестов в двух разных сетях.В таблице 3 указано количество узлов, количество ссылок, количество зон и общие потребности в перемещении. Все наборы данных доступны исследователям. (https://github.com/bstabler/TransportationNetworks). Сеть Су-Фолс использовалась во многих публикациях для решения проблемы распределения трафика [12]. В Су-Фоллс 76 каналов, 24 узла, 552 сохранения ограничений потока и 1824 ограничения неотрицательности
Суфоллс Анахайм
24 416
76914
24 38
360600.0 104694.4
CR IP T
Сеть
PT
ED
M
AN US
сеть. Сеть Анахайма состоит из 914 каналов, 416 узлов и 38 зон. Две сети показаны на Рисунке 4 (a) и Рисунке 4 (b) соответственно.
(b) Сеть Анахайма
CE
(a) Сеть SiouxFalls
Рис. время в пути, полное время в пути, полученное из предложенной модели Physarum. На рисунках 5 и 6 показаны сети SiouxFalls и Anaheim соответственно. На рисунках показан поток по четырем линиям с наивысшим потоком, время прохождения по соответствующим ссылкам, общее время прохождения и значение трех критериев, соответственно. Как показано на Рисунке 20
На рисунках 5 и 6 показаны сети SiouxFalls и Anaheim соответственно. На рисунках показан поток по четырем линиям с наивысшим потоком, время прохождения по соответствующим ссылкам, общее время прохождения и значение трех критериев, соответственно. Как показано на Рисунке 20
ПРИНЯТОЕ РУКОВОДСТВО
CR IP T
5 и 6, поток трафика и время прохождения четырех каналов сходятся в состав после нескольких итераций. Поток трафика каждого канала, рассчитанный с помощью предложенного алгоритма и алгоритма FW, показан в Таблице 4 и на Рисунке 7 соответственно.По сравнению с алгоритмом FW, предложенный алгоритм Physaruminspired получает те же потоки трафика. В Таблице 5 указывается общее время движения транспортного средства U BD и относительная ошибка ERT на итерации. Ясно, что общее время в пути быстро приближается к нижней границе. Таблица 4: Равновесные потоки, рассчитанные с помощью предложенного алгоритма на сети Су-Фолс Q (103)
Link
Q (103)
Link
Q (103)
Link
Q (103)
( 1, 2) (3, 1) (4, 5) (5, 9) (7, 8) (8, 9) (9, 10) (10, 16) (11, 12) (12, 13) ( 14, 15) (15, 19) (16, 17) (17, 19) (19, 15) (20, 19) (21, 22) (22, 21) (23, 24)
4. 4945 8.0945 18.0068 15.7812 12.1012 6.8824 21.7448 11.0469 8.3654 12.2881 9.0363 19.0836 11.6939 9.9528 19.1171 8.7098 8.6188 8.6069 7.9028
4945 8.0945 18.0068 15.7812 12.1012 6.8824 21.7448 11.0469 8.3654 12.2881 9.0363 19.0836 11.6939 9.9528 19.1171 8.7098 8.6188 8.6069 7.9028
(1, 3) (3, 4) (4, 11) (6, 2) (7, 18) ) (10, 9) (10, 17) (11, 14) (13, 12) (14, 23) (15, 22) (16, 18) (18, 7) (19, 17) (20, 21 ) (21, 24) (22, 23) (24, 13)
8,1189 14,0068 5,2000 5,9919 15,7966 8,3886 21,8145 8,1000 9,7764 12,3794 8,4002 18,4094 15,2805 15,8573 9,9417 6,3023 10,3095 9,6618 11,1122
) (3, 12, 2, 2, 5, 4) (6, 5) (8, 6) (9, 5) (10, 11) (11, 4) (12, 3) (13, 24) (15, 10) (16, 8) ( 17, 10) (18, 16) (19, 20) (20, 22) (22, 15) (23, 14) (24, 21)4.5189 10,0226 18,0307 8,8065 12,5254 15,7969 17,7266 5,3000 9,9742 11,1209 23,1929 8,4066 8,1000 15,3354 8,6874 7,0000 18,3857 8,3945 10,2595
(2, 6) (4, 3) (5, 6) (6, 8) (8, 7) (6, 8) (8, 7) ) (10, 15) (11, 10) (12, 11) (14, 11) (15, 14) (16, 10) (17, 16) (18, 20) (20, 18) (21, 20 ) (22, 20) (23, 22) (24, 23)
5.9674 14.0307 8.7983 12.4928 12.0405 6.8363 23. 1267 17.6041 8.4052 9.8142 9.0798 11.0728 11.6829 18.9793 18.9950 6.2404 7.0000 9.6261 7.8613
1267 17.6041 8.4052 9.8142 9.0798 11.0728 11.6829 18.9793 18.9950 6.2404 7.0000 9.6261 7.8613
000 США
000
Link
Таблица 5: Общее время в пути транспортного средства для различных итераций
LBD (106)
CE
Итерация
7.480225
RET (10−2) 3,494 1,014 0,074 0,003
AC
10 50100200
Су-Фоллс, шт. 1,332618 1,321999 1,322378 1,322085
RET (10-2) 0,778 0,025 0,004 0,018
В частности, REQ сети Анахайма не сходится на Рисунке 6 (d). Это является результатом некоторых звеньев, подобных Q53,406, показанных на рисунке 8. Когда поток звена приближается к нулю, поток изменяется с небольшим шагом, относительная ошибка ERQ находится в толчке.Например, REQ = 105, когда Q553,406 1 = 10−12 и Q553,406 2 = 10−7. Однако критерии остановки, cr.2 и cr.3, associ21
ПРИНЯТО РУКОВОДСТВО
2,15 2,1
0
1000
2000
Итерация
3000
(c)
× 106 8
L 10,9
6 4 0
ED
4 2
0
1000
2000
2000
3000
1
кр. 2
2
1e-05
cr.1
cr.3
3000
0
Итерация
1000
2000
3000
1e-10
Итерация
Рисунок 5: Реальный трафик сеть
AC
CE
1000
L 9,10
Итерация
M
6
0
L 10,15
(d)
8
PT
Общий ход время10
Q 9,10
12
AN US
Q 10,9
2.2
CR IP T
Q 10,15
Время в пути
14
2,3 2,25
(б) L 15,10
16
Q 15,10
2,35
Транспортный поток
(a)
× 104
Относительная ошибка
2,4
, связанная не только с потоком трафика, но и с временем в пути, показывает значительную преждевременную конвергенцию.
22
ПРИНЯТАЯ РУКОВОДСТВО
Q 233232
0
100
200
2
1
M
0.8
100
0
100
200
1e + 5
cr. 2
2
cr.1
1
1e-05
cr.3
200
0 9000
50
100
150
200
Итерация
Рисунок 6: Реальная сеть трафика
AC
CE
0
L 4233
(d)
ED L 233,232
Итерация
(c)
PT
Общее время прохождения
× 106
1.2
0,6
L 62,2
AN US
Q 4233 Итерация
1,4
2,5
1,5
1,2 1,15
L 63,62
CR IP T
Q 63,62
1,3
Время в пути
3
1,35
1,25
(б)
3,5
Q 62,2
1,4
Поток трафика
(а)
× 104
× 104
× 104 относительная погрешность
1.45
4.3. Пример 3 В этом примере мы сравниваем производительность предложенного алгоритма с характеристиками FW, BFW и CFW. На рисунках 9 и 10 показаны характеристики сходимости различных алгоритмов в сети Sioux Falls23
ПРИНЯТОЕ РУКОВОДСТВО
3/4519
1
2
11/18031
15/8806
4
000 4
000 6
52/11684
60
/1 8
99
3
58/9942
43/23192
17
57/19117
19 7 97 56 10005
67/18386
71/8395
61/8711
ED
70/9662
23
22
65/8620
63/7 0
00
66
00
62/6302
21
20 64/6240
AC
75/10260
/7 0
59/8688
69/8607
73/7903 76/8607
78/7903
72/9626
68
Рисунок 7: Equi Потоки librium, рассчитанные с помощью алгоритма FW, в сети Sioux Falls
work и сети Anaheim, соответственно. Из рисунка 9, когда уровень 24
Из рисунка 9, когда уровень 24
54/15855
47/8407
26/21814
AN US
35/9974
31/5300
M
00
45/19083 46 / 18410
42/8400
37/12288
PT
/8 1
00
53/9953
28/23126
34/9776
40/9814
000 51 80002000 51 80005
000 1
15
74/11112
18 50/15278
49/11695
30
44/9080
41/9036
CE
55/15334
16
16
14
39/11121
22/8389
25/21744
48/11073
10
32/17604
7
20/12041
18/15794
20005 7/1002227/17727
36/8405
13
17/12102
8
24/6837
11
38/12379
16/12493
13/15781
21/6883
9
33/8365
12
12/8798
72 180066/14006
19/12526
8/14031
3
CR IP T
5/8095
4/5967
2/8119
14/5992
5ПРИНЯТОЕ РУКОВОДСТВО
10-2
CR IP T
10-4
10-6
10-8
AN US
Линейный поток
Q 53,406
10-10
14 20
25
30
M
10-12
35
40
45
50
55
60
ED
Итерационная сеть
Рис.
AC
CE
PT
RET или REL достигает 10−4, усл. Все алгоритмы, основанные на FW, начинают работать медленно.Однако RET предлагаемого алгоритма может быстро достигать 10-5, что показывает, что предложенная модель имеет явное преимущество перед всеми другими тремя алгоритмами в определении равновесного решения. Из рисунка 10 (а) видно, что предложенный алгоритм на самом деле имеет лучшую производительность сходимости, чем алгоритмы на основе FW, когда относительная ошибка REL больше 10-4. Как показано на рисунке 10 (a), потоки ссылок, полученные из предложенной модели, вдохновленной Physarum, сходятся быстрее, чем потоки основанных на FW алгоритмов, когда относительная ошибка REL больше 10−4.Прежде всего, предложенная модель, вдохновленная Physarum, очень эффективна как с точки зрения точности, так и с точки зрения времени выполнения.
25
ПРИНЯТОЕ РУКОВОДСТВО
100
FW CFW BEW Предлагаемый метод
10-4
CR IP T
-2
REL
RET
100 10
Предлагаемый метод FW10-5
10-6
0
5
10
15
0
5
Время (секунды)
10
15
Время (
секунд)
) Относительная ошибка REL
AN US
(a) Относительная ошибка RET
Рисунок 9: Характеристики сходимости различных алгоритмов в сети Sioux Falls
100
100
FW CFW BEW Предлагаемый метод
20
40
60
PT
0
ED
RET 10-4
80
100
REL
10-2
M
10-2 9000W
M
10-2 9000W
Предложение d метод
10-4
10-6
120
Время (сек)
0
20
40
60
80
100
120
Время (сек)
(b) Относительная ошибка REL
CE
(a) Относительная ошибка RET
Рисунок 10: Характеристики сходимости различных алгоритмов в сети Anaheim
AC
5. ВЫВОДЫ Для решения проблемы назначения трафика UE в этой статье предлагается модифицированная модель, основанная на Physarum, для назначения трафика UE. Принимая во внимание пищевое поведение Physarum, равновесные потоки могут быть получены, когда Physarum не может найти более короткое время прохождения между каждой парой OD. Модифицированный алгоритм 26
ВЫВОДЫ Для решения проблемы назначения трафика UE в этой статье предлагается модифицированная модель, основанная на Physarum, для назначения трафика UE. Принимая во внимание пищевое поведение Physarum, равновесные потоки могут быть получены, когда Physarum не может найти более короткое время прохождения между каждой парой OD. Модифицированный алгоритм 26
ACCEPTED MANUSCRIPT
CR IP T
более эффективен в сетях с реальным трафиком с характеристиками двустороннего трафика и несколькими парами OD. Путем декомпозиции потоков в соответствии с исходным узлом можно различать потоки из разных пар OD.По сравнению с FW, BFW и CFW предложенная модель, вдохновленная Physarum, очень эффективна как с точки зрения точности, так и с точки зрения времени выполнения
AN US
В будущем одна из наших работ – использовать параллельные вычисления и оптимальную модель. для линейной системы уравнений [58], чтобы сократить время вычислений. Кроме того, в рамках нашего исследования также рассматривается вопрос о том, как применить модель Physarum к сети динамического трафика и сети трафика с эластичным спросом.
Благодарность
PT
Ссылки
ED
M
Работа частично поддержана Национальным фондом естественных наук Китая (грант No.61671384), План фундаментальных исследований естествознания в провинции Шэньси в Китае (программа № 2016JM6018), Фонд SAST (программа № SAST2016083), Seed Foundation инноваций и творчества для аспирантов Северо-Западного политехнического университета (программа № Z2016122 ).
CE
[1] Д. П. Берцекас, Э. М. Гафни, Методы проектирования для вариационных неравенств с применением к задаче распределения трафика, в: Недифференциальные и вариационные методы в оптимизации, Springer, 1982, стр.139–159.
AC
[2] М. Папагеоргиу, Динамическое моделирование, назначение и руководство маршрутом в транспортных сетях, Транспортные исследования, часть B: Методологические 24 (1990) 471–495. [3] А. Зилиаскопулос, Модель линейного программирования для задачи оптимального динамического распределения трафика в системе с одним пунктом назначения, Транспортная наука 34 (2000) 37–49.
27
ПРИНЯТАЯ РУКОВОДСТВО
[4] Ю. Лю, Дж. Бункер, Л. Феррейра, Моделирование выбора маршрута для транзитных пользователей при назначении транзита: обзор, Transport Reviews 30 (2010) 753–769.
CR IP T
[5] W.-B. Ду, X.-L. Чжоу, О. Лордан, З. Ван, К. Чжао, Я.-Б. Чжу, Анализ китайской сети авиакомпаний как многоуровневых сетей, Транспортные исследования Часть E: Обзор логистики и транспорта 89 (2016) 108–116. [6] Дж. Г. Уордроп, Некоторые теоретические аспекты исследования дорожного движения, в: Inst Civil Engineers Proc London / UK /, стр. 72–73.
AN US
[7] М. Дж. Бекманн, К. Б. Макгуайр, К. Б. Винстен, Т. К. Купманс, Исследования по экономике транспорта, Economic Journal 26 (1956) 820–821.
[8] С. В. Чиу, Эффективный алгоритм для оптимального проектирования управления пространственным трафиком с сетевыми потоками, Прикладное математическое моделирование 33 (2009) 2710–2722.
M
[9] М. Флориан, И. Константин, Д. Флориан, Новый взгляд на метод прогнозируемого градиента для задания равновесия, Отчет об исследованиях в области транспорта: Журнал Совета по исследованиям в области транспорта (2009) 10–16.
Флориан, Новый взгляд на метод прогнозируемого градиента для задания равновесия, Отчет об исследованиях в области транспорта: Журнал Совета по исследованиям в области транспорта (2009) 10–16.
ED
[10] С. В. Чиу, Эффективный алгоритм для вычисления равновесия трафика с использованием модели транзита, Прикладное математическое моделирование 34 (2010) 3390–3399.
PT
[11] Д. Ю. Лин, П. В. Леонг, Пользовательское равновесие n-пути для транспортных сетей, Прикладное математическое моделирование 38 (2014) 667C682.
CE
[12] Л. Дж. Леблан, Э. К. Морлок, У. П. Пирскалла, Эффективный подход к решению проблемы распределения трафика в равновесной дорожной сети, Транспортные исследования 9 (1975) 309–318.
AC
[13] Д. У. Хирн, С. Лофонгпанич, Дж. Вентура, Конечность в ограниченном симплициальном разложении, Письма об исследовании операций 4 (1985) 125–130.[14] Т. Ларссон, М. Патриксон, Симплициальная декомпозиция с дезагрегированным представлением для задачи распределения трафика, Наука о транспорте 26 (1992) 4–17.
28
ПРИНЯТАЯ РУКОВОДСТВО
[15] М. Митраджиева, П. О. Линдберг, «Жесткое движение», сопряженное направление, методы Фрэнка-Вульфа с приложениями к распределению трафика, Транспортная наука 47 (2013) 280–293.
CR IP T
[16] С. Рю, А. Чен, К. Чой, модифицированный алгоритм проекции градиента для решения задачи распределения трафика с эластичным спросом, Computers & Operations Research 47 (2014) 61–71.
[17] Р. Джаякришнан, В. Т. Цай, Дж. Н. Прашкер, С. Раджадхьякша, Более быстрый алгоритм на основе маршрута для назначения трафика, Транспортный центр Калифорнийского университета (1994).
AN US
[18] Л. Ченг, Й. Иида, Н. Уно, У. Ван, Альтернативные квазиньютоновские методы для определения равновесия пользователя с учетом емкости, Отчет об исследованиях в области транспорта: Журнал Совета по исследованиям в области транспорта (2003) 109 –116.
M
[19] К. Сан, Р. Джаякришнан, В. Цай, Вычислительное исследование алгоритма, основанного на путях, и его вариантов для статического назначения трафика, Протокол исследования транспорта: Журнал Совета по исследованиям транспорта (1996) 106 –115.
ED
[20] М. Татинени, Х. Эдвардс, Д. Бойс, Сравнение дезагрегированного симплициального разложения и алгоритмов Фрэнка-Вульфа для выбора оптимального маршрута пользователем, Протокол исследования транспорта: Журнал Совета по исследованиям транспорта (1998) 157–162.
PT
[21] Х. Бар-Гера, Алгоритмы на основе происхождения для моделирования транспортных сетей. Национальный институт статистических наук Research Park Nc (1999).
CE
[22] Х. Бар-Гера, Алгоритм на основе происхождения для задачи распределения трафика, Транспортная наука 36 (2002) 398–417.
AC
[23] Р. Б. Диал, Алгоритм назначения трафика на основе равновесия пользователя, который исключает хранение и перечисление путей, Транспортные исследования, часть B: Методологические методы 40 (2006) 917–936. [24] М. Сюй, А. Чен, З. Гао, Усовершенствованный алгоритм на основе происхождения для решения комбинированной задачи распределения и назначения, Европейский журнал операционных исследований 188 (2008) 354–369.
29
ПРИНЯТАЯ РУКОВОДСТВО
[25] М. Маттеуччи, Л. Муссоне, Система муравьиной колонии для анализа равновесия транспортных пользователей в перегруженных сетях, Swarm Intelligence 7 (2013) 255–277.
CR IP T
[26] Л. Дачьерно, М. Галло, Б. Монтелла, Алгоритм оптимизации муравьиной колонии для решения проблемы асимметричного распределения трафика, Европейский журнал операционных исследований 217 (2012) 459–469.
AN US
[27] Дж. Дж. Санчес-Медина, М. Диас-Кабрера, М. Дж. Галан-Морено, Э. Рубио Ройо, Исследование равновесия пользователей системы оптимизации маршрута путешествий AETROS, in: MorenoDiaz, R and Pichler, F and QuesadaArencibia , A (Ed.), Computer Aided Systems Theory – Eurocast 2011, PT II, volume 6928 of Lecture Notes in Computer Science, Springer-Verlag Berlin, Heidelberger Platz 3, D-14197 Berlin, Germany, 2012, pp.465–472. [28] А. Адацки, Машины Physarum: инкапсуляция реакции-диффузии для вычисления остовного дерева, Naturwissenschaften 94 (2007) 975–980.
M
[29] А. Адамацки, Дж. Джонс, Программируемая реконфигурация машин Physarum, Natural Computing 9 (2010) 219–237.
ED
[30] А. Адамацки, Машины Physarum: компьютеры из слизи, том 74, World Scientific, 2010. [31] С.Л. Стефенсон, Х. Стемпен, Myxomycetes: справочник по слизевикам, Bioscience 45 (1995). ) 601–602.
PT
´ T´oth, Интеллект: решение лабиринта [32] Т. Накагаки, Х. Ямада, A. амебовидный организм, Nature 407 (2000) 470–470.
CE
[33] А. Теро, С. Такаги, Т. Сайгуса, К. Ито, Д. П. Беббер, М. Д. Фрикер, К. Юмики, Р. Кобаяси, Т. Накагаки, Правила для биологически вдохновленного адаптивного дизайна сети. , Science 327 (2010) 439–442.
AC
[34] В. Бонифачи, К. Мельхорн, Г. Варма, Physarum может вычислять кратчайшие пути, в: Симпозиум Acm-Siam по дискретным алгоритмам, с.121C133. [35] А. Адацки, Слизневая плесень решает лабиринт за один проход, чему способствует градиент хемоаттрактантов., IEEE Transactions on Nanobioscience 11 (2012) 131–4.
30
ПРИНЯТОЕ РУКОВОДСТВО
[36] Х. Ван, Х. Лу, Х. Чжан, К. Ван, Й. Дэн, Биологический метод решения задачи кратчайшего с ограничениями, The Scientific World Journal 2014 ( 2014).
CR IP T
[37] X. Zhang, Y. Zhang, Y. Deng, Улучшенный био-вдохновленный алгоритм для задачи направленного кратчайшего пути, Bioinspiration & Biomimetics 9 (2014).
[38] Q. Ван, X. Лу, X. Чжан, Y. Deng, C. Xiao, Механизм ожидания для задачи кратчайшего пути на основе Physarum polycephalum, Международный журнал общих систем 44 (2015) 326–340 .
AN US
[39] А. Адамацки, Биооценка мировых транспортных сетей, Биооценка мировых транспортных сетей 43 (2012) 368. [40] А. Адамацки, М. Лис, П. Слот, Биоразвитие автомагистралей. сеть в Нидерландах: подход к слизистой плесени, Advances in Complex Systems 16 (2013) 1250034.
М
[41] М.-А. И. Цомпанас, Г. К. Сиракулис, А. И. Адамацки, Physarum в кремнии: исследование автомагистралей Греции, Natural Computing (2014) 1–17.
ED
[42] В. Евангелидис, М. А. Цомпанас, Г. К. Сиракулис, А. Адамацки, Слизистая плесень имитирует развитие римских дорог на Балканах, Journal of Archaeological Science Reports 2 (2015) 264–281.
PT
[43] А. Шуман, А. Адамацки, Логическое моделирование Physarum polycephalum, препринт arXiv arXiv: 1105.4060 (2011).
CE
[44] А. Шуман, А. Адацки, Пространственная логика Physarum, Новая математика и естественные вычисления 7 (2011) 483–498.
AC
[45] Э. Браунд, Э. Миранда, Музыка с нетрадиционными вычислениями: система для синтеза звука Physarum polycephalum, в: International Symposium on Computer Music Modeling and Retrieval, Springer, pp. 175–189. [46 ] Э. Р. Миранда, Использование интеллекта Physarum polycephalum для нетрадиционных компьютерных музыкальных композиций., IJUC 10 (2014) 251–268.
31
ПРИНЯТО РУКОВОДСТВО
CR IP T
[47] Э. Браунд, Э. Миранда, Музыка с нетрадиционными вычислениями: к пошаговому секвенсору из плазмодия Physarum polycephalum, в: Международная конференция по эволюционной и биологически вдохновленной музыке и Art, Springer, стр. 15–26. [48] Й. Чжан, З. Чжан, Й. Дэн, С. Махадеван, Биологически вдохновленное решение нечетких задач кратчайшего пути, Прикладные мягкие вычисления 13 (2013) 2356–2363.
15–26. [48] Й. Чжан, З. Чжан, Й. Дэн, С. Махадеван, Биологически вдохновленное решение нечетких задач кратчайшего пути, Прикладные мягкие вычисления 13 (2013) 2356–2363.
AN US
[49] X. Zhang, Q. Wang, A. Adamatzky, FT Chan, S. Mahadevan, Y. Deng, Биологически вдохновленный алгоритм оптимизации для решения задач нечеткого кратчайшего пути со смешанной длиной нечеткой дуги, Журнал теории оптимизации и приложений 163 (2014) 1049–1056. [50] W. Jiang, Y. Luo, X. Qin, J. Zhan, Улучшенный метод ранжирования обобщенных нечетких чисел с различной высотой слева и справа, Journal of Intelligent & Fuzzy Systems 28 (2015) 2343–2355.
M
[51] X.Чжан, А. Адацки, Ф. Т. Чан, Ю. Дэн, Х. Ян, X.-С. Ян, М.-А. И. Цомпанас, Г. С. Сиракулис, С. Махадеван, Биологически вдохновленная модель проектирования сети, Научные отчеты 5 (2015).
ED
[52] Х. Чжан, Эффективный алгоритм Physarum для решения проблемы назначения трафика с помощью двух критериев, Международный журнал нетрадиционных вычислений 11 (2015) 473–490.
PT
[53] А. Теро, Р. Кобаяши, Т. Накагаки, Математическая модель адаптивной транспортной сети в поиске путей истинной слизистой плесени, Журнал теоретической биологии 244 (2007) 553–564.
CE
[54] У. Г. Хансен, Как доступность влияет на землепользование, Журнал Американского института планировщиков 25 (1959) 73–76.
AC
[55] Д. Бойс, Б. Ралевич-Декич, Х. Бар-Гера, Конвергенция транспортных назначений: сколько достаточно?, Журнал транспортной инженерии 130 (2004) 49–55. [56] З. Чжоу, А. Бриньоне, М. Кларк, Вычислительное исследование альтернативных методов для задания статического равновесия трафика, в: Труды Всемирной конференции по исследованию транспорта (WCTRS), Лиссабон, Португалия.32
ПРИНЯТОЕ РУКОВОДСТВО
[57] А. Адамацки, Дж. Джонс, На пути к роботам Physarum: вычисления и манипулирование на поверхности воды, Journal of Bionic Engineering 5 (2008) 348–357.
AC
CE
PT
ED
M
AN US
CR IP T
[58] И. Кутис, Г.Л. Миллер, Р. Пенг, Приближение к оптимальности для решения линейных систем SDD, в: Основы компьютерных наук (FOCS), 51-й ежегодный симпозиум IEEE, 2010 г., IEEE, стр.235–244.
Кутис, Г.Л. Миллер, Р. Пенг, Приближение к оптимальности для решения линейных систем SDD, в: Основы компьютерных наук (FOCS), 51-й ежегодный симпозиум IEEE, 2010 г., IEEE, стр.235–244.
33
Страница не найдена – ScienceDirect
Пандемия COVID-19 и глобальное изменение окружающей среды: новые потребности в исследованиях
Environment International, том 146, январь 2021 г., 106272
Роберт Баруки, Манолис Кожевинас, […] Паоло Винеис
Исследование количественной оценки риска изменения климата в городском масштабе: обзор последних достижений и перспективы будущего направления
Обзоры возобновляемых и устойчивых источников энергии, Том 135, Январь 2021 г., 110415
Бинь Йеа, Цзинцзин Цзян, Чжунго Лю, И Чжэн, Нань Чжоу
Воздействие изменения климата на экосистемы водно-болотных угодий: критический обзор экспериментальных водно-болотных угодий
Журнал экологического менеджмента,
Том 286, 15 мая 2021 г. , 112160
, 112160
Шокуфе Салими, Сухад А.A.A.N. Алмуктар, Миклас Шольц
Обзор воздействия изменения климата на общество в Китае
Достижения в исследованиях изменения климата, Том 12, выпуск 2, апрель 2021 г., страницы 210-223
Юн-Цзянь Дин, Чен-Ю Ли, […] Цзэн-Ру Ван
Общественное мнение об изменении климата и готовности к стихийным бедствиям: данные Филиппин
2020 г.
Винченцо Боллеттино, Тилли Алкайна-Стивенса, Манаси Шарма, Филип Ди, Фуонг Пхама, Патрик Винк
Воздействие бытовой техники на окружающую среду в Европе и сценарии снижения их воздействия
Журнал чистого производства, Том 267, 10 сентября 2020 г., 121952
Роланд Хишье, Франческа Реале, Валентина Кастеллани, Серенелла Сала
Влияние глобального потепления на смертность апрель 2021 г.
Раннее человеческое развитие, Том 155, апрель 2021 г., 105222
Жан Каллея-Агиус, Кэтлин Инглэнд, Невилл Каллеха
Понимание и противодействие мотивированным корням отрицания изменения климата
Текущее мнение об экологической устойчивости,
Том 42, февраль 2020 г. , страницы 60-64
, страницы 60-64
Габриэль Вонг-Пароди, Ирина Фейгина
Это начинается дома? Климатическая политика, нацеленная на потребление домашних хозяйств и поведенческие решения, является ключом к низкоуглеродному будущему
Энергетические исследования и социальные науки Том 52, июнь 2019, страницы 144-158
Гислен Дюбуа, Бенджамин Совакул, […] Райнер Зауэрборн
Трансформация изменения климата: определение и типология для принятия решений в городской среде
Устойчивые города и общество, Том 70, июль 2021 г., 102890
Анна К. Херлиманн, Саре Мусави, Джеффри Р. Браун
«Глобальное потепление» против «изменения климата»: повторение связи между политической самоидентификацией, формулировкой вопроса и экологическими убеждениями.
Журнал экологической психологии, Том 69, июнь 2020, 101413
Алистер Раймонд Брайс Сауттер, Рене Мыттус
| импортировать lsst.dax.data_generator.columns как столбцы | ||
| из lsst.dax.data_generator import Chunker, UniformSpatialModel | ||
| num_stripes = 200 | ||
| num_substripes = 5 | ||
| chunker = Chunker (0, num_stripes, num_substripes) | ||
| edge_width = 0.017 # градусов, должно быть> = перекрытие | ||
| спец = { | ||
| «Объект»: { | ||
| «столбцы»: { | ||
“objectId”: columns. ObjIdGenerator (), ObjIdGenerator (), | ||
| “ra, decl”: столбцы.RaDecGenerator (), | ||
| “uPsFlux, gPsFlux, rPsFlux, iPsFlux, zPsFlux, yPsFlux”: | ||
| столбцов.MagnitudeGenerator (n_mags = 6), | ||
| “uPsFluxErr, gPsFluxErr, rPsFluxErr, iPsFluxErr, zPsFluxErr, yPsFluxErr”: | ||
| столбцов.UniformGenerator (min_val = 0,05, max_val = 0,5, n_columns = 6, column_seed = 6), | ||
| “psLnL, psChi2, psN”: столбцы.UniformGenerator (n_columns = 6, column_seed = 7), | ||
| «uBbdRa, uBdRaErr, uBdDecl, uBdDeclErr, uBdE1, uBdE1Err, uBdE2, uBdE2Err, uBdFluxB, uBdFluxBErr, uBdFluxD, uBdFluxDErr, uBdReB, uBdReBErr, uBdReD, uBdReDErr, uBdLnL, uBdChi2, uBdN, gBbdRa, gBdRaErr, gBdDecl, gBdDeclErr, gBdE1, gBdE1Err, gBdE2, gBdE2Err, gBdFluxB, gBdFluxBErr, gBdFluxD, gBdFluxDErr, gBdReB, gBdReBErr, gBdReD, gBdReDErr, gBdLnL, gBdChi2, gBdN, rBbdRa, rBdRaErr, rBdDecl, rBdDeclErr, rBdE1, rBdE1Err, rBdE2, rBdE2Err, rBdFluxB, rBdFluxBErr, rBdFluxD, rBdFluxDErr, rBdReB, rBdReBErr, rBdReD, rBdReDErr, rBdLnL, rBdChi2, rBdN, iBbdRa, iBdRaErr, iBdDecl, iBdDeclErr, iBdE1, iBdE1Err, iBdE2, iBdE2Err, iBdFluxB, iBdFluxBErr, iBdFluxD, iBdFluxDErr, iBdReB, iBdReBErr, iBdReD, iBdReDErr, iBdLnL, iBdChi2, IBDN, zBbdRa, zBdRaErr, zBdDecl, zBdDeclErr, zBdE1, zBdE1Err, zBdE2, zBdE2Err, zBdFluxB, zBdFluxBErr, zBdFluxD, zBdFluxDErr, zBdReB, zBdReBErr, zBdReD, zBdReDErr, zBdLnL, zBdChi2, zBdN, yBbdRa, yBdRaErr, yBdDecl, yBdDeclErr, yBdE1, yBdE1Err, yBdE2, yBdE2Err, yBdFluxB, yBdFluxBErr, yBdFluxD, yBdFluxDErr, yBdReB, yBdReBErr, yBdReD, yBdBdLDRN2, yBdBd18DERN, yBdBd18DeRN | ||
| столбцов.UniformGenerator (n_columns = 114, column_seed = 8), | ||
| “ugStd, ugStdErr, grStd, grStdErr, riStd, riStdErr, izStd, izStdErr, zyStd, zyStdErr”: | ||
| столбцов.UniformGenerator (min_val = -2, max_val = 2, n_columns = 10, column_seed = 9), | ||
| “uRa, uRaErr, uDecl, uDeclErr, gRa, gRaErr, gDecl, gDeclErr, rRa, rRaErr, rDecl, rDeclErr, iRa, iRaErr, iDeclr, zaRDeclR, yDeclr, год, zaEclEr” : | ||
| столбцов.UniformGenerator (n_columns = 24, column_seed = 10), | ||
| «UE1, uE1Err, UE2, uE2Err, uE1_E2_Cov, GE1, gE1Err, ge2, gE2Err, gE1_E2_Cov, rE1, rE1Err, rE2, rE2Err, rE1_E2_Cov, IE1, iE1Err, ie2, iE2Err, iE1_E2_Cov, ZE1, zE1Err, Ze2, zE2Err, zE1_E2_Cov, yE1, yE1Err, yE2, yE2Err, yE1_E2_Cov “: | ||
| столбцов.UniformGenerator (min_val = -1, max_val = 1, n_columns = 30, column_seed = 11), | ||
| «uMSum, uMSumErr, gMSum, gMSumErr, rMSum, rMSumErr, iMSum, iMSumErr, zMSum, zMSumErr, yMSum, yMSumErr, uM4, gM4, rM4, iM4, zM41814M4»: | ||
| столбцов.UniformGenerator (min_val = -1, max_val = 1, n_columns = 18, column_seed = 12), | ||
| «uPetroRad, uPetroRadErr, gPetroRad, gPetroRadErr, rPetroRad, rPetroRadErr, iPetroRad, iPetroRadErr, zPetroRad, zPetroRadErr, yPetroRad, yPetroRadErr, petroFilter, uPetroFlux, uPetroFluxErr, gPetroFlux, gPetroFluxErr, rPetroFlux, rPetroFluxErr, iPetroFlux, iPetroFluxErr, zPetroFlux, zPetroFluxErr, yPetroFlux, yPetroFluxErr, uPetroRad50, uPetroRad50Err, gPetroRad50, gPetroRad50Err, rPetroRad50, rPetroRad50Err, iPetroRad50, iPetroRad50Err, zPetroRad50, zPetroRad50Err, yPetroRad50, yPetroRad50Err, uPetroRad90, uPetroRad90Err, gPetroRad90, gPetroRad90Err, rPetroRad90, rPetroRad90Err, iPetroRad90, iPetroRad90Err, zPetroRad90, zPetroRad90Err, yPetroRad90, yPetroRad90Err» : | ||
| столбцов.UniformGenerator (max_val = 10, n_columns = 49, column_seed = 13), | ||
| «uKronRad, uKronRadErr, gKronRad, gKronRadErr, rKronRad, rKronRadErr, iKronRad, iKronRadErr, zKronRad, zKronRadErr, yKronRad, yKronRadErr, kronFilter, uKronFlux, uKronFluxErr, gKronFlux, gKronFluxErr, rKronFlux, rKronFluxErr, iKronFlux, iKronFluxErr, zKronFlux, zKronFluxErr, yKronFlux, yKronFluxErr, uKronRad50, uKronRad50Err, gKronRad50, gKronRad50Err, rKronRad50, rKronRad50Err, iKronRad50, iKronRad50Err, zKronRad50, zKronRad50Err, yKronRad50, yKronRad50Err, uKronRad90, uKronRad90Err, gKronRad90, gKronRad90Err, rKronRad90, rKronRad90Err, iKronRad90, iKronRad90Err, zKronRad90, zKronRad90Err, yKronRad90, yKronRad90Err» : | ||
| столбцов.UniformGenerator (max_val = 10, n_columns = 49, column_seed = 14), | ||
| “uApN, gApN, rApN, iApN, zApN, yApN, протяженность, FLAGS1, FLAGS2”: | ||
| столбцов.UniformGenerator (max_val = 1, n_columns = 9, column_seed = 15), | ||
| }, | ||
| «плотность»: UniformSpatialModel (50000), | ||
| }, | ||
| «Принудительный источник»: { | ||
| «prereq_tables»: [«CcdVisit», «Object»], | ||
| «столбцы»: { | ||
| “objectId, ccdVisitId, psFlux, psFlux_Sigma”: | ||
| столбцов.ForcedSourceGenerator (visit_radius = 1.7, filters = “ugriz”), | ||
| }, | ||
| } | ||
| } | ||
| spec [“CcdVisit”] = { | ||
| “from_file”: “visit_table.csv”, | ||
| “столбцы”: “ccdVisitId, filterName, ra, decl” | ||
| } |
Диалектическая поведенческая терапия (DBT) | CAMH
Что такое диалектическая поведенческая терапия (ДПТ)?
Диалектический означает «существование противоположностей».«В DBT людей учат двум, казалось бы, противоположным стратегиям: принятие (то есть, что их опыт и поведение действительны) и изменение (то есть, что они должны вносить позитивные изменения, чтобы управлять эмоциями и двигаться вперед).
DBT делится на четыре этапа лечения. Этапы определяются тем, насколько сурово поведение человека.
- На стадии 1 человек часто несчастен, и его поведение выходит из-под контроля. Цель состоит в том, чтобы человек перешел от выхода из-под контроля к достижению контроля над поведением.
- На стадии 2 человек может чувствовать, что живет в тихом отчаянии: его опасное для жизни поведение находится под контролем, но он продолжает страдать. Цель состоит в том, чтобы помочь человеку перейти от тихого отчаяния к полному эмоциональному переживанию.
- На этапе 3 задача состоит в том, чтобы научиться жить: определять жизненные цели, развивать самоуважение и обрести покой и счастье. Цель состоит в том, чтобы человек жил обычной жизнью, полной счастья и несчастья.
- Некоторым людям необходим этап 4.Цель состоит в том, чтобы найти более глубокий смысл в духовном существовании.
Как работает диалектическая поведенческая терапия (ДПТ)?
Стандартная программа DBT требует годичного обязательства. Более короткие программы, иногда называемые «программами на основе DBT», используют некоторые методы или структуру DBT и могут быть очень полезны для определенных людей.
Стандартная программа DBT обычно состоит из пяти компонентов, каждый из которых выполняет определенную функцию:
- Группа по обучению навыкам DBT проводится под руководством специалиста по психотерапевту в формате группы, аналогичном классу.Задачи предназначены для практики между занятиями. Цель состоит в том, чтобы помочь людям внедрить в свою жизнь эффективные и практические навыки, которые они могут использовать, когда они в беде. Эти навыки призваны заменить другое нездоровое и негативное поведение. Класс обычно собирается один раз в неделю на 2,5 часа. Для прохождения полного курса обучения навыкам требуется 24 недели, которые часто повторяются для создания годичной программы. В классе преподаются четыре навыка:
- внимательность: практика присутствия в настоящем и признания мыслей, чувств и поведения по мере их возникновения, не пытаясь их контролировать.
- терпимость к бедствию: процесс обучения тому, как справляться с кризисом, особенно когда его невозможно изменить, и принятие ситуации такой, какая она есть, а не такой, какой она должна быть.
- межличностная эффективность: способность спрашивать о том, что человеку нужно, и отказываться при необходимости, сохраняя при этом самоуважение и отношения с другими.
- регулирование эмоций: способность управлять эмоциями так, чтобы они не контролировали мысли и поведение.
- Индивидуальная Психотерапия направлена на повышение мотивации и помощь людям в применении навыков к конкретным проблемам и событиям в их жизни. Эти занятия дают возможность человеку и терапевту собраться вместе и обсудить свои индивидуальные цели. Сеансы обычно проводятся еженедельно продолжительностью от 60 до 90 минут.
- Коучинг в данный момент использует коучинг по телефону и другой коучинг в реальной жизни («in vivo») для оказания поддержки в данный момент.Терапевт научит человека пережить стрессовое событие и побудит его использовать свои навыки ДПТ. Цель состоит в том, чтобы обеспечить обобщение навыков и их применение в повседневной жизни человека.
- Стратегии ведения дел дают человеку возможность контролировать свою жизнь и заботу. Терапевт применяет выученные стратегии, чтобы научить человека быть автономным и руководить своим делом.
- Консультационная группа DBT сосредоточена на поддержке людей, которые проводят DBT, включая терапевтов, терапевтов, кураторов и других.Консультационная группа призвана помочь терапевтам оставаться мотивированными и компетентными, чтобы они могли предоставить наилучшее возможное лечение. Команда помогает друг другу, управляя выгоранием и делясь знаниями.
Цель всех этих элементов – помочь человеку построить жизнь, которой, по его мнению, стоит жить.
Обучение навыкам
Это предназначено для людей с пограничным расстройством личности, у которых в сообществе есть терапевт, которого они посещают как минимум раз в две недели.
Участники этой программы будут посещать еженедельную группу по обучению навыкам DBT, которую ведет терапевт в формате группы, аналогичном классу. Упражнения предназначены для людей, чтобы отработать навыки между занятиями. Цель состоит в том, чтобы помочь людям внедрить в свою жизнь эффективные и практические навыки, которые они могут использовать, когда они в беде. Эти навыки призваны заменить другое нездоровое и негативное поведение. Класс обычно собирается один раз в неделю на 2 часа. Чтобы пройти полный курс обучения навыкам, требуется 24 недели.В классе преподается четыре навыка:
- Внимательность: практика присутствия в настоящем и признания мыслей, чувств и поведения по мере их возникновения, не пытаясь их контролировать
- Терпимость к бедствию: процесс обучения тому, как справляться во время кризиса, особенно когда его невозможно изменить, и принятие ситуации такой, какая она есть, а не такой, какой она должна быть
- Эффективность межличностного общения: способность спрашивать о том, что человеку нужно, и говорить «нет» при необходимости, сохраняя при этом самоуважение и отношения с другими
- Регулирование эмоций: способность управлять эмоциями, чтобы они не контролировали мысли и поведение.
Кому может помочь диалектическая поведенческая терапия (ДПТ)?
DBT был разработан для людей с пограничным расстройством личности. Но он может помочь людям с другими проблемами психического здоровья, включая суицидальное поведение, членовредительство, употребление психоактивных веществ, посттравматическое стрессовое расстройство (ПТСР), депрессию и расстройства пищевого поведения.
Часто задаваемые вопросы
Чем DBT отличается от когнитивно-поведенческой терапии (CBT)?
И DBT, и CBT – это формы психотерапии.В рамках этих методов лечения человек разговаривает со специалистом по психическому здоровью о своих проблемах и приобретает навыки, которые помогут им справиться с ними. Однако КПТ в первую очередь фокусируется на изучении способов изменить бесполезные мысли и поведение. DBT учит людей принимать свои мысли, чувства и поведение, а также методам их изменения. В DBT преподаются не только личные навыки, но и навыки межличностных отношений.
DBT основан на CBT, но больше фокусируется на эмоциональных и социальных аспектах жизни.Фактически, DBT был создан, чтобы помочь людям справиться со своими сильными эмоциями.
Источники:
Что такое диалектическая поведенческая терапия (ДБТ)? © 2017 Behavioral Tech
В чем разница между CBT и DBT? © 2015 Canadian Mental Health Association, BC Division
Диалектическая поведенческая терапия (DBT) © 2017 Mind
Диалектическая поведенческая терапия (DBT) © 2017 SANE Australia




 ;
; py на главном сервере · lsst-dm / dax_data_generator · GitHub
py на главном сервере · lsst-dm / dax_data_generator · GitHub