Категория: Разное

Центр вращения это: центр вращения – это… Что такое центр вращения?

   17.04.1980  Комментировать

Содержание

центр вращения – это… Что такое центр вращения?

центр вращения
centre of rotation

Большой англо-русский и русско-английский словарь. 2001.

  • центр вписанной сферы
  • центр выборки

Смотреть что такое “центр вращения” в других словарях:

  • центр вращения — sukimosi centras statusas T sritis fizika atitikmenys: angl. center of gyration; center of rotation vok. Drehpunkt, m; Rotationszentrum, n rus. точка вращения, f; центр вращения, m pranc. centre de rotation, m …   Fizikos terminų žodynas

  • мгновенный центр вращения — Точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному.

    Примечание. В каждый момент времени мгновенный центр вращения совпадает с мгновенным центром… …   Справочник технического переводчика

  • оптический центр вращения глаза — Z′ Неподвижная точка внутри глаза, вокруг которой глаз вращается при изменении направления взгляда. Примечание Оптический центр вращения схематического глаза находится на расстоянии 14,43 мм от передней вершины роговицы. [ГОСТ 14934 88]… …   Справочник технического переводчика

  • МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ — точка плоской неизменяемой фигуры, совершающей непо ступат. движение в своей плоскости, скорость к рой в данный момент времени равна 0. М. ц. в. лежит на пересечении прямых, проведённых в разл. точках фигуры перпендикулярно векторам скоростей… …   Большой энциклопедический политехнический словарь

  • мгновенный центр вращения — Точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному …   Политехнический терминологический толковый словарь

  • Центр — Государственное унитарное предприятие города Москвы Московский городской Центр арендного жилья . Источник …   Словарь-справочник терминов нормативно-технической документации

  • ЦЕНТР — (лат. centrum, от греч. kentron). 1) средоточие, средина круга, шара и проч. 2) политическая партия в Германии, в качестве протеста против дальнейшего развития германского союза во имя независимости церкви от государственной власти. Словарь… …   Словарь иностранных слов русского языка

  • ЦЕНТР — ЦЕНТР, центра, муж. (греч. kentron, букв. острие). 1. Точка сосредоточения каких нибудь отношений в фигуре (мат., мех.). Центр окружности или шара (точка пересечения их диаметров, равно удаленная от всех точек окружности или поверхности шара).… …   Толковый словарь Ушакова

  • центр записи — Центр вращения носителя записи или сигналограммы, имеющих форму диска или пластины при записи, воспроизведении. [ГОСТ 13699 91] Тематики запись и воспроизведение информации …   Справочник технического переводчика

  • центр записи — 166 центр записи: Центр вращения носителя записи или сигналограммы, имеющих форму диска или пластины при записи, воспроизведении Источник: ГОСТ 13699 91: Запись и воспроизведение информации. Термины и определения оригинал …   Словарь-справочник терминов нормативно-технической документации

  • ЦЕНТР УДАРА — точка тела, имеющего неподвижную ось вращения, обладающая тем свойством, что удар, направленный в эту точку перпендикулярно к плоскости, проходящей через ось вращения и центр масс тела, не передаётся на ось и не оказывает ударных воздействий на… …   Физическая энциклопедия


МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ – это… Что такое МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ?

МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ

точка плоской неизменяемой фигуры, совершающей непо-ступат. движение в своей плоскости, скорость к-рой в данный момент времени равна 0. М. ц. в. лежит на пересечении прямых, проведённых в разл. точках фигуры перпендикулярно векторам скоростей этих точек в рассматриваемый момент времени.

Большой энциклопедический политехнический словарь. 2004.

  • МГНОВЕННОЕ ВЗРЫВАНИЕ
  • МЕГА…

Смотреть что такое “МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ” в других словарях:

  • мгновенный центр вращения — Точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному. Примечание. В каждый момент времени мгновенный центр вращения совпадает с мгновенным центром… …   Справочник технического переводчика

  • мгновенный центр вращения — Точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному …   Политехнический терминологический толковый словарь

  • Мгновенный центр скоростей — Мгновенный центр скоростей  при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Содержание 1 Положение… …   Википедия

  • Центр в физике — В механике понятие о Ц. или связано с понятием о симметрии (см. Ось) вокруг него, или с понятием о месте приложения равнодействующей некоторой совокупности сил, приложенных к твердому телу. В кинематике. При рассмотрении скоростей точек какой… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Центр (физ.) — В механике понятие о Ц. или связано с понятием о симметрии (см. Ось) вокруг него, или с понятием о месте приложения равнодействующей некоторой совокупности сил, приложенных к твердому телу. В кинематике. При рассмотрении скоростей точек какой… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Трение качения — Трение качения  сопротивление движению, возникающее при перекатывании тел друг по другу. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном. В большинстве случаев величина трения… …   Википедия

  • Радиационные пояса Земли —         внутренние области земной магнитосферы, в которых магнитное поле Земли удерживает заряженные частицы (Протоны, Электроны, Альфа частицы), обладающие кинетической энергией от десятков кэв до сотен Мэв (в разных областях Р. п. З. энергия… …   Большая советская энциклопедия

  • РАДИАЦИОННЫЕ ПОЯСА ЗЕМЛИ — внутренние области земной магнитосферы, в к рых магн. поле Земли удерживает заряж, ч цы (протоны, эл ны, альфа частицы и ядра более тяжёлых хим. элементов), обладающие кинетич. энергией от десятков кэВ до сотен МэВ. Выходу заряж. ч ц из Р. п. 3.… …   Физическая энциклопедия

  • СТРУКТУРА МЕХАНИЗМОВ — см. также о словаре аксоид аналог скорости точки аналог углового ускорения звена а …   Теория механизмов и машин

  • Кинематика — наука, изучающая состояние движения независимо от вызывающих его сил и получившая название от греческого слова κίνημα состояние движения и составляющая часть общей науки о движении механики. Цель ее состоит в изучении геометрических свойств… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Центр вращения – Энциклопедия по машиностроению XXL

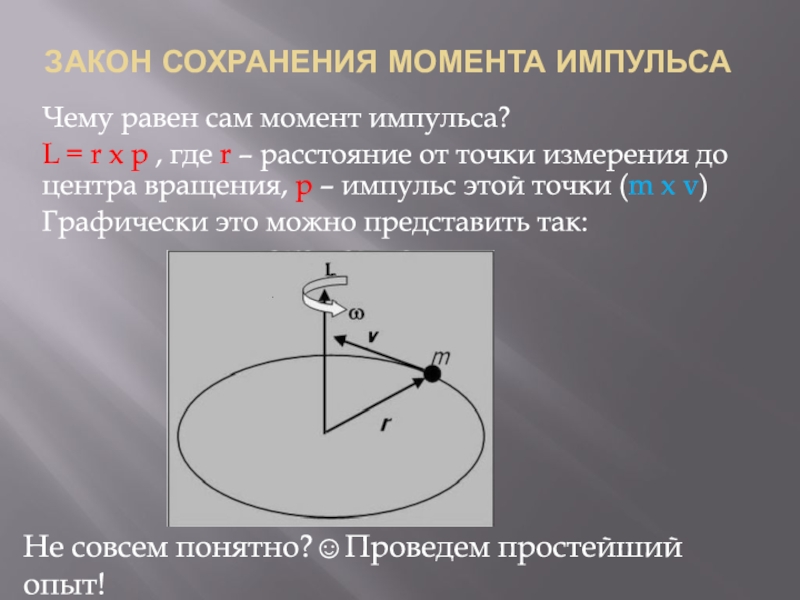
Г. Мгновенным центром скоростей Р, в движении звена i относительно звена k называется точка звена г, скорость которой в этом движении равна нулю. В каждый момент времени движение звена / относительно звена k можно рассматривать как вращение около мгновенного центра вращения — около точки звена k, с которой в рассматриваемый момент совпадает мгновенный центр скоростей Pih- Для определения положения мгновенного центра скоростей в движении звена i относительно звена k требуется знать направления относительных скоростей двух точек звена i. Мгновенный центр скоростей Р,- находится на пересечении  
[c.62]
Рассмотрим примеры на определение мгновенных центров вращения (центров скоростей) в относительном движении звеньев механизма.  [c.62]

При неподвижном звене 4 направления скоростей точек В С перпендикулярны соответственно линиям АВ и D, поэтому точка пересечения этих линий является искомым мгновенным центром вращения (скоростей) Рц звена 2 относительно звена 4.  [c.62]

Для нахождения мгновенного центра вращения (скоростей) в движении звена 3 относительно звена J остановим звено 1, а остальные звенья сделаем подвижными. Теперь векторы скоростей центров шарниров С и D будут направлены соответственно перпендикулярно линиям ВС и AD. Продолжая эти линии, получим точку их пересечения, которая и будет искомым центром вращения (скоростей) Рз5 в движении звена 3 относительно звена 1.  

[c.62]

Пример 2. Для кулисного механизма Витворта (рис. 29) найти мгновенный центр вращения (скоростей) звена 2 (ползуна) относительно звена 4 (стойки) — точку Р2 ,  [c.62]

Для кривошипно-ползунного механизма найти мгновенные центры вращения (скоростей) и ускорений звена ВС (звена 2) в его движении относительно стойки (звена 4). Дано 1лв = 50 мм, 1вс — 150 мм, Ф1 = 90°, угловая скорость кривошипа АВ постоянна.  [c.64]
Для кривошипного механизма с качающимся ползуном найти мгновенные центры вращения (скоростей) и ускорений звена  [c.
64]

Для шестизвенного механизма найти мгновенный центр вращения (скоростей) звена 4 в его движении относительно стойки (звена 6).  [c.65]

Найдем на плоскости Qj звена 2 точку Рги скорость которой 8 рассматриваемом движении звена 2 будет равна нулю, т. е. найдем мгновенный центр вращения звена 2 в его движении относительно звена 1. Точка P i, очевидно, лежит на линии, проходящей через центр вращения звена /, т. е. через точку Оц и перпендикулярной скорости звена 2, слева от точки Oi (рис. 101). Расстояние R от точки Р21 до точки Oi найдется из условия  [c.188]

Oi на угол Аф по направлению угловой скорости —ш, и займет положение у Оу. Мгновенный центр вращения Р ,, в этом положении находится аналогичным построением.  [c.188]

Теперь звено 2 как бы остановилось, а звено I участвует в двух движениях движется поступательно со скоростью —V2 и вращается вокруг центра Oi с угловой скоростью o)j. Мгновенный центр вращения Р будет лежать на линии, перпендикулярной скорости На и проходящей через центр вращения Oi слева от него (в данном положении точка Рп будет совпадать с точкой Расстояние R находится из соотношения (19. 1).  [c.188]

Постоянное расстояние между центрами вращения звеньев равно /о.о, = 100 мм.  [c.192]

Для осуществления заданного постоянного передаточного отношения зададимся на звене I, выбранном нами, профилем Кх — К, который в рассматриваемый момент времени проходит через мгновенный центр вращения (полюс зацепления) Р 2- Найдем на звене 2 сопряженный заданному профиль — К . который удовлетворял бы следующему условию где бы ни соприкасались профили Ki — Ki и /С2 — / 2, нормаль к ним, проведенная через точку их касания, должна проходить через постоянный полюс зацепления Ру -  [c.193]

Пример 2. Спроектировать трехзвенную зубчатую передачу с внешним зацеплением зубьев (колеса — прямозубые), у которой модуль /п= 1,0 мм, расстояние между центрами вращения колес Л,.д = 18 мм, передаточное отношение i i2 = 1,52 (после подбора чисел зубьев фактическое передаточное отношение не должно отличаться от заданного на 2,5%).  [c.206]

В и д I (рис. 117, а) — кулачковый механизм с поступательно движущимся толкателем, имеющим ролик или острие на своем конце ось толкателя проходит через центр вращения вала кулачка.  [c.214]

Во всех задачах, где на конце толкателя имеется ролик, следует вначале рассматривать кулачковый механизм с толкателем, имеющим острие, которое совпадает с центром вращения ролика, т, е. вначале следует спроектировать центровой (теоретический) профиль кулачка.  [c.214]

Для кулачкового механизма IV вида найти радиус-вектор точки профиля кулачка, которая находится в месте касания профиля кулачка с концом толкателя при повороте кулачка на угол Ф1 = 60° из положения, указанного на чертеже, если начальный угол отклонения толкателя от линии центров АС равен Фо = 30°, ход толкателя Ф = 30°, расстояние между центрами вращения кулачка и толкателя L = 80 мм, длина толкателя I = 60 мм, закон изменения второй производной от функции положения толкателя задан графиком  [c. 230]

Из теоретической механики известно, что при плоскопараллельном движении твердого тела (звена механизма) это движение в каждый момент времени может быть представлено как вращение вокруг некоторой точки, называемой мгновенным центром вращения. В механизмах мы можем рассматривать движение звеньев относительно стойки и относительно любого из звеньев механизма. Если движение звена относительно стойки принять за абсолютное движение, то соответствующий мгновенный центр вращения будем называть мгновенным центром вращения в абсолютном движении рассматриваемого звена. Если же рассматривается движение звена относительно любого подвижного звена механизма, то соответствующий мгновенный центр вращения будем называть мгновенным центром вращения в относительном движении рассматриваемых звеньев.  [c.64]


На рис. 4.1 изображена схема механизма шарнирного четырех-звенника. Мгновенные центры вращения звеньев 2 w 4 относительно стойки 1 совпадают соответственно с точками А а D. Обозначим эти центры соответственно через Рз, и Р4,. Мгновенным центром вращения звена 3 относительно звена 2 является точка В, которую мы обозначим через Наконец, мгновенный центр  [c.64]

ЦеНТр вращения Р должен одновременно венного вращения  [c.65]

Как было показано выше, для любого механизма в любом его положении могут быть определены все мгновенные центры вращения в абсолютном и в относительном движениях его звеньев. Следовательно, если имеется механизм, воспроизводящий то или иное движение, то такое же движение звеньев может быть осуществлено механизмом, представляющим собой две сопряженные центроиды.  [c.67]

J°. В 14 нами был рассмотрен вопрос об определении мгновенных центров вращения звеньев механизмов. Для многозвенных механизмов эта задача усложняется том, что для определения мгновенного центра вращения одного из промежуточных звеньев механизма обычно приходится определять мгновенные центры и всех остальных звеньев. Поэтому в некоторых случаях удобно 4  [c.99]

Когца отрезок ВС займет положение В С, мгновенный центр вращения займет положение Фигуры OBP fi и ОВ — прямоугольники, у которых диагонали равны длине отрезка ВС поэтому центроидой при движении отрезка ВС относительно сторон угла хОу будет окружность Д21 с центром в точке О и радиусом, равным ВС.  [c.63]

Для четырехшарнирного четырехзвенного механизма найти мгновенные центры вращения (скоростей) и ускорений шатуна ВС (звена 2) в его движении относительно стойки (звена 4). Дано 1ав — 70л1Л , /со 150 мм, Iad — 1вс — 200 мм, Фх = 15°, угловая скорость кривошипа А В постоянна.  [c.64]

Для механизма муфты Ольдгейма найти мгновенный центр вращення (скоростей) звена 2 в его движении относительно стойки (звена 4), если / с = 80 мм, Ф1 = 30 .  [c.65]

Равномерное вращательное движение звена при совпадении центра мисс S ввена с его центром вращения А (рис. 46, е).  [c.79]

Для того чтобы найти мгновенный центр вращения в двнженни одного знен i относительно другого, удобно воспользоваться методом обращения движения. Этот метод состоит в том, что всем звеньям механизма сообщается скорость,  [c.187]

В последующий момент времени звено / переместится вдоль линии уО на величину As в направлении скорости —Vz и центр вращения его займет положение 0[. Мгновенный центр вращения P. j находится аналогично тому, как ранее был найден мгновенный центр вран1,ения Pi – Соединив точки Рц, Р[з и т. д. плавной кривой, получим центроиду Д12 в движении звена 1 относительно звена 2.  [c.188]

Пример. Спроектировать передачу (рис. 105, о), осуществляющую заданное движение звеньев / и 2 посредством центроид в относительном движении. Звено I вращается равпомерпо, а звено 2 вращается с угловой скоростью (/) в соответствии с графиком (рис. 105, б). За время Т одного оборота звена / звено 2 гоже совершает один оборот.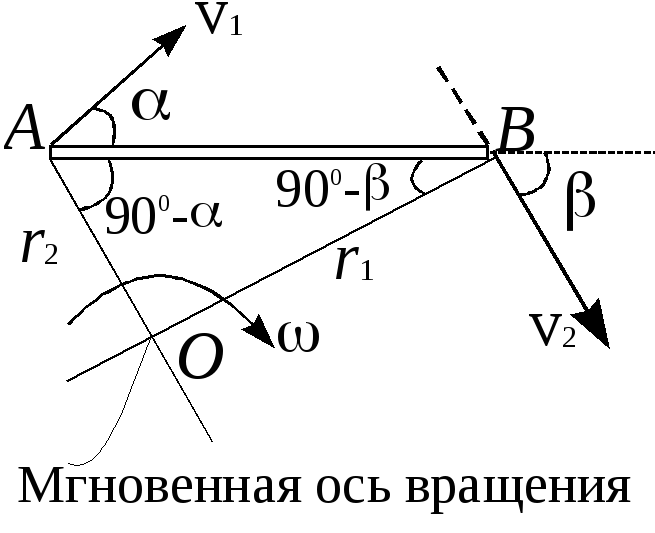 Расстояние между центрами вращения звеньев 0.0. = 200 мм.  [c.188]

Спроектировать передачу, осуществляющую залЯанное движение звеньев / н2 посредством центроид в относительном движении, если звено / должно вращаться равномерно с угловой скоростью i, а звено 2 — с угловой скоростью о)з, изменяющейся в соответствии с графиком, показанным на чертеже. За время Т одного оборота звена 1 звено 2 также совершает один оборот. Расстояние между центрами вращения звеньев равно 1о,о, — 100 мм. Звенья вращаются в противоположных направлениях.  [c.192]

Случай третий. Формулы для расчета исправленного внешнего зацеп-ленн , когда заданы модуль т, передаточное отношение и расстояние между центрами вращения колес Л б-  [c.203]

Чтобы найти мгновенный центр вращения звена 5 относительно стойки 1, следует продолжить линии В А и D, точка пересечения которых Рз1 и оказывается центром мгновенного вращения звена 3 относительно стойки 1. Как известно из теоретической механики, мгновеннь Й центр вращения располагается на пересечении перпендикуляров к направлениям скоростей точек звена. В изображенном на рис. 4.1 механизме линии АВ D как раз и являются перпендикулярами к векторам скоростей точек В м С.  [c.65]

Установленное свойство мгновенных центров вращения позволяет определить все мгновенные центры вращения заданного ме.ханизма. Пусть нам дан крипошипно-ползунный механизм (рис, 4.2). Обозначим в точках А, В и С мгновенные центры вращения Р21, Рз2 И 4з- Мгновенный центр Р находится в бесконечности на прямой, перпендикулярной к оси х — х движения ползуна 4. Соединяем мгновенные центры вращения P i и Р . и продолжаем прямую РцРз2 ДО пересечения в точке Р с прямой 43 41- т. е. прямой, перпендикулярной к направляющей л — л-(точка Рц располагается в бесконечности), получаем мгновенный центр вращения P i звена 3 относительно звена I. Для нахождения мгновенного це1ггра вращения Р42 в движении звена 4 относительно звена 2 соединяем мгновенные центры вращения Р43 и Р32 и продолжаем эту прямую до пересечения в точке Р с прямой, соединяющей мгновенные центры вращения Р21 и Рц, т. е. с прямой, проведенной через точку Рц перпендикулярно к направляющей X — X.  [c.65]

Нп р[ С. 4.3 И 4.4 показаны мг ювеиаые центры вра ценпя двух кулнсиих механизмов. Мгновенный центр вращения Яд4 (рис. 4.3) находится в бесконечности и лежит на прямой, перпендикулярной к прямой СВ.  [c.66]


Как известно из теоретической механики, геометрическое месго мгновенных центров вращения образует так называемую центроиду.  [c.66]

Как известно из теоретической механики, при вращательном плоском движении звена около некоторой точки ускорения всех точек звена пропорциональны радиусам-векторам, соединяюи нм исследуемые точки с центром вращения, а направления этих ускорении образуют с этими радиусами-векторами постоянный угол i, определяемый из уравнения  [c.85]

Описание и примеры стандартных функций SVG

Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0

Основные преимущества формата SVG.

Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW

Бесконечное полотно документа svg.

Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.

При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.

 

Взаимодействие SVG, XML с HTML, CSS, Jscript

В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.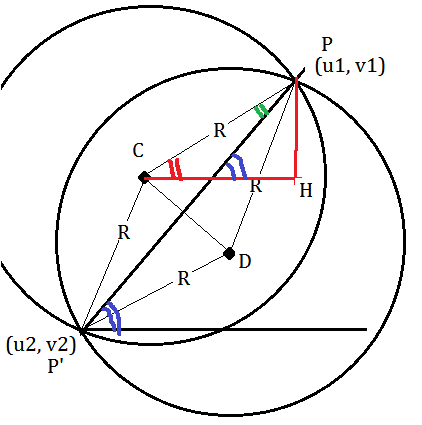
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.

Анимация и интерактивность SVG.

Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton. mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.

Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js

Еще примеры анимации ⇛

Недостатки SVG формата

  • С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
  • Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
  • В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
    Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.


 

 

UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛

Мгновенный центр вращения в теоретической механике

Мгновенный центр вращения:

Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.

Рис. 71

Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение. Можно ввести угловую скорость вращения вокруг мгновенного центра вращения или, точнее, вокруг мгновенной оси, проходящей через мгновенный центр вращения и перпендикулярной плоскости движения.

При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой,— подвижной центроидой. Для каждого плоского движения фигуры существуют свои две центроиды: подвижная и неподвижная. Очевидно, что точка плоской фигуры, с которой в рассматриваемый момент совпадает мгновенный центр вращения, имеет скорость, равную нулю; следовательно, она является в то же время мгновенным центром скоростей.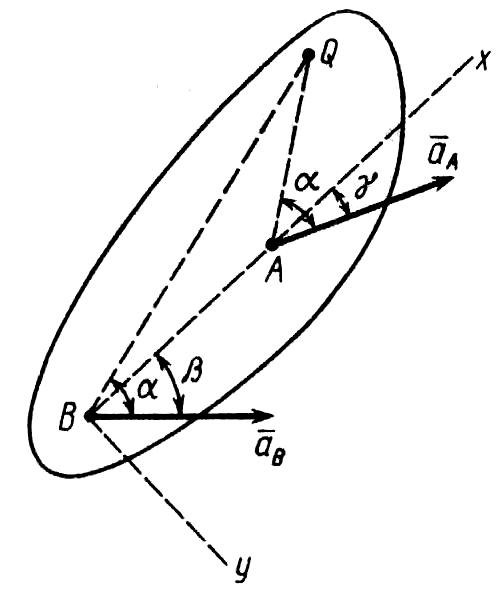

При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.

Центроиды нашли применение в некоторых вопросах кинематики механизмов. Рассмотрим пример нахождения центроид.

Пример:

Стержень

Решение. Скорость точки может быть направлена только по , а точки —только по , так как траекториями этих точек являются указанные прямые. Восстанавливая перпендикуляры в точках и к этим направлениям, получаем положение точки , которая и будет мгновенным центром скоростей на подвижной плоскости, скрепленной со стрежнем, и мгновенным центром вращения на неподвижной плоскости. Из рисунка видно, что во все время движения, как диагональ прямоугольника. Следовательно, неподвижная центроида является окружностью радиусом   с центром в точке .

На подвижной плоскости , скрепленной со стрежнем , точка обладает аналогичным геометрическим свойством, так как , поэтому подвижной центроидой является окружность радиуса  с центром в точке .

При качении подвижной окружности по неподвижной концы и диаметра окружности движутся прямолинейно соответственно по прямым и . Повернув на произвольный угол вокруг точки  в плоскости чертежа оси координат и рассмотрев этот случай после закрепления осей координат в новом положении, можно убедиться, что центроидами являются те же окружности. Следовательно, другие две точки подвижной окружности движутся прямолинейно.

Таким образом убеждаемся, что все точки подвижной окружности движутся по прямым линиям, проходящим через центр неподвижной окружности . Это свойство точек подвижной окружности можно использовать для преобразования вращательного движения в прямолинейное поступательное движение.

Рис. 72

В общем случае движения плоской фигуры мгновенный центр скоростей— точка — и мгновенный центр ускорений —точка — являются различными точками этой фигуры (рис. 72). Эти точки совпадают, если плоское движение вырождается во вращательное движение вокруг неподвижной оси.

Выберем точку плоской фигуры и отметим точки и . Поставим задачу — указать формулы, по которым можно вычислить проекции ускорения точки на оси  и , и . Ось перпендикулярна оси и . Точка является мгновенным центром ускорений. Следовательно, ускорение

и направлено всегда к точке ; проекция ускорения на перпендикулярное направление

Точка является мгновенным центром скоростей. Скорость точки перпендикулярна , а скорость всегда направлена по касательной к траектории. Следовательно, ось есть касательная к траектории и проекция ускорения на нее является касательным ускорением и вычисляется по формуле для касательного ускорения

Ось перпендикулярна касательной; следовательно, это главная нормаль траектории. Проекция ускорения на это направление вычисляется по формуле для нормального ускорения

Если , то траектория точки обращена выпуклостью к точке ; если , то вогнутостью.

Кажется, что у точки два различных нормальных и касательных ускорения. Но  и — касательное и нормальное ускорения абсолютного движения точки по отношению к неподвижной системе координат (на рис. 72 не показана), a и — соответственно касательное и нормальное ускорения относительного движения точки по отношению к подвижной системе координат, движущейся поступательно относительно неподвижной вместе с точкой . Переносное ускорение точки  совпадает с абсолютным ускорением точки , а оно равно нулю, так как эта точка фигуры является мгновенным центром ускорений.

Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Впервые измерена скорость вращения черной дыры в центре нашей Галактики

https://ria.ru/20201021/galaktika-1580823905.html

Впервые измерена скорость вращения черной дыры в центре нашей Галактики

Впервые измерена скорость вращения черной дыры в центре нашей Галактики – РИА Новости, 21.10.2020

Впервые измерена скорость вращения черной дыры в центре нашей Галактики

Американские астрофизики впервые смогли рассчитать скорость вращения сверхмассивной черной дыры, расположенной в центре галактики Млечный Путь. Результаты… РИА Новости, 21.10.2020

2020-10-21T14:22

2020-10-21T14:22

2020-10-21T14:22

наука

космос – риа наука

открытия – риа наука

физика

астрофизика

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn21.img.ria.ru/images/07e4/0a/15/1580814549_0:31:1281:751_1920x0_80_0_0_5d567506b5bc983c93defbbe0dbd4973.jpg

МОСКВА, 21 окт — РИА Новости. Американские астрофизики впервые смогли рассчитать скорость вращения сверхмассивной черной дыры, расположенной в центре галактики Млечный Путь. Результаты исследования опубликованы в журнале The Astrophysical Journal Letters.В центре нашей Галактики находится сверхмассивная черная дыра Стрелец А (SgrA*). За ее открытие ученым Райнхарду Гензелю и Андреа Гез в этом году была присуждена Нобелевская премия по физике. Они же вычислили, что масса SgrA* составляет около четырех миллионов солнечных масс.Второй важнейший параметр, характеризующий черную дыру и имеющий важное значение при формировании и эволюции галактики — скорость вращения, или спин, до последнего времени был неизвестен. Влияние вращения черной дыры на орбиты ближайших звезд незначительно, поэтому его трудно измерить напрямую.Вместо этого исследователи из Центра астрофизики Гарвардского и Смитсоновского института (CfA) и Центра междисциплинарных исследований и исследований в области астрофизики Северо-Западного университета (CIERA) изучили орбиты и пространственное распределение S-звезд — ближайших к черной дыре звезд, вращающихся вокруг нее.Авторы установили, что S-звезды организованы в две плоскости типа звездных дисков, вращающихся в разных направлениях. По мнению исследователей, это указывает на то, что скорость вращения самой SgrA* невелика — если бы она обладала значительным вращением, орбитальные плоскости звезд со временем испытывали бы смещение, но этого не наблюдается. По оценкам ученых спин черной дыры составляет не более 0,1.”Для нашего исследования мы использовали недавно обнаруженные S-звезды, чтобы показать, что спин черной дыры SgrA* меньше, чем 10 процентов от ее максимального значения, что соответствует вращению со скоростью света, — приводятся в пресс-релизе CfA слова одного из двух авторов исследования профессора Абрахама Леба (Abraham Loeb). — В противном случае общие орбитальные плоскости этих звезд не оставались бы выровненными в течение их жизни, как мы это видим сегодня”.”Черные дыры выделяют огромное количество энергии, которая удаляет газ из галактик”, — продолжает второй автор статьи Джакомо Фраджионе (Giacomo Fragione) из CIERA.При этом образуются мощные пучки лучей — квазарные струи, или джеты. Но авторы считают, что от сверхмассивной черной дыры в центре Млечного Пути вряд ли стоит ожидать таких струй, так как она слишком медленно вращается.”Считается, что струи приводятся в движение быстро вращающимися черными дырами, которые действуют как гигантские маховики”, — объясняет Леб.Ученые надеются, что более точные данные о скорости вращения черной дыры SgrA* они смогут получить, когда будет полностью реализован проект по созданию глобальной сети радиотелескопов Телескоп горизонта событий (Event Horizon Telescope), цель которого — наблюдение за непосредственным окружением сверхмассивной черной дыры в центре Млечного Пути.

https://ria.ru/20201020/galaktika-1580682349.html

https://ria.ru/20201012/zvezda-1579434892.html

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2020

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

Новости

ru-RU

https://ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

https://cdnn21.img.ria.ru/images/07e4/0a/15/1580814549_119:0:1160:781_1920x0_80_0_0_96e103a21663d6bee4b77c64619d3215.jpg

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

космос – риа наука, открытия – риа наука, физика, астрофизика

МОСКВА, 21 окт — РИА Новости. Американские астрофизики впервые смогли рассчитать скорость вращения сверхмассивной черной дыры, расположенной в центре галактики Млечный Путь. Результаты исследования опубликованы в журнале The Astrophysical Journal Letters.

В центре нашей Галактики находится сверхмассивная черная дыра Стрелец А (SgrA*). За ее открытие ученым Райнхарду Гензелю и Андреа Гез в этом году была присуждена Нобелевская премия по физике. Они же вычислили, что масса SgrA* составляет около четырех миллионов солнечных масс.

Второй важнейший параметр, характеризующий черную дыру и имеющий важное значение при формировании и эволюции галактики — скорость вращения, или спин, до последнего времени был неизвестен. Влияние вращения черной дыры на орбиты ближайших звезд незначительно, поэтому его трудно измерить напрямую.

Вместо этого исследователи из Центра астрофизики Гарвардского и Смитсоновского института (CfA) и Центра междисциплинарных исследований и исследований в области астрофизики Северо-Западного университета (CIERA) изучили орбиты и пространственное распределение S-звезд — ближайших к черной дыре звезд, вращающихся вокруг нее.

Авторы установили, что S-звезды организованы в две плоскости типа звездных дисков, вращающихся в разных направлениях. По мнению исследователей, это указывает на то, что скорость вращения самой SgrA* невелика — если бы она обладала значительным вращением, орбитальные плоскости звезд со временем испытывали бы смещение, но этого не наблюдается. По оценкам ученых спин черной дыры составляет не более 0,1.

20 октября 2020, 16:38НаукаОбнаружены доказательства столкновения Млечного Пути с другой галактикой

“Для нашего исследования мы использовали недавно обнаруженные S-звезды, чтобы показать, что спин черной дыры SgrA* меньше, чем 10 процентов от ее максимального значения, что соответствует вращению со скоростью света, — приводятся в пресс-релизе CfA слова одного из двух авторов исследования профессора Абрахама Леба (Abraham Loeb). — В противном случае общие орбитальные плоскости этих звезд не оставались бы выровненными в течение их жизни, как мы это видим сегодня”.

“Черные дыры выделяют огромное количество энергии, которая удаляет газ из галактик”, — продолжает второй автор статьи Джакомо Фраджионе (Giacomo Fragione) из CIERA.

При этом образуются мощные пучки лучей — квазарные струи, или джеты. Но авторы считают, что от сверхмассивной черной дыры в центре Млечного Пути вряд ли стоит ожидать таких струй, так как она слишком медленно вращается.

“Считается, что струи приводятся в движение быстро вращающимися черными дырами, которые действуют как гигантские маховики”, — объясняет Леб.

Ученые надеются, что более точные данные о скорости вращения черной дыры SgrA* они смогут получить, когда будет полностью реализован проект по созданию глобальной сети радиотелескопов Телескоп горизонта событий (Event Horizon Telescope), цель которого — наблюдение за непосредственным окружением сверхмассивной черной дыры в центре Млечного Пути.

12 октября 2020, 16:14НаукаАстрономы впервые наблюдали смерть звезды в черной дыре

Что такое центр вращения?

Колесо обозрения

Колесо обозрения

Когда вы смотрите на колесо обозрения, вы замечаете, что оно вращается вокруг своего центра на стержне. Это почти похоже на спиннер на игровой доске. Часть посередине остается неподвижной, и вертушка перемещается вокруг нее. Если вы смотрели изображение вращающегося колеса обозрения, то его часть, которая остается в центре во время вращения или вращения, называется центром вращения .Если бы это было настоящее колесо обозрения или любой трехмерный объект, центр вращения был бы назван осью .

Не всегда средний

На двухмерном чертеже центр вращения не обязательно должен быть посередине изображения, как это было с колесом обозрения. Помните, это как раз тот момент, когда картинка включается. Например, если вы воткнете булавку в маленькую букву А на изображении красного Х и повернете бумагу по кругу, А будет центром вращения, потому что все изображение Х будет вращаться вокруг булавки.

Возьмите карандаш и нарисуйте любой рисунок на листе бумаги. Теперь поместите карандаш в любом месте нарисованного вами рисунка. Держите карандаш прямо вверх, чтобы только грифель касался бумаги. Поверните картинку по кругу вокруг острия карандаша, не поднимая карандаш. Когда вы поднимаете карандаш, точка, которую оставляет карандаш на бумаге, становится центром вращения. Картинка вращалась или поворачивалась вокруг нее.

Теперь переместите карандаш в другое место на фотографии. Держите его там и снова переверните бумагу вокруг точки.На этот раз новая точка, сделанная вашим карандашом, будет центром вращения. Фактически, куда бы вы ни положили карандаш и повернули бумагу, оно становится центром вращения. Центр вращения меняется в зависимости от того, где находится точка.

Центр вращения коровы?

Корова спиннинг

А теперь нарисуем корову или распечатаем ее. Посмотри, сможешь ли ты сделать центр вращения коровьим носом! Для этого вам нужно приложить кончик карандаша к носу коровы.Теперь переверните бумагу так, чтобы карандаш был центром вращения. Она перевернется вверх ногами и боком! Она может стоять на носу. Теперь давайте сделаем центр вращения в верхней части ее задней части, где соединяется хвост. Начни вращаться – вот она, вверх ногами!

Итак, если бы это была корова из пенополистирола (мы бы никогда не сделали этого с настоящей коровой!), Мы могли бы сделать ось. Если мы возьмем длинный шест, воткнем его в пенополистирольную корову и закрутим по кругу, мы получим ось. Эта ось была бы полюсом, точно так же, как ось колеса обозрения была бы стержнем.

Резюме урока

Центр вращения – это точка, в которой поворачивается изображение. Или, говоря другими словами, если вы попытаетесь удерживать бумагу неподвижно карандашом и повернуть бумагу, место, где ваш карандаш оставляет отметку, будет центром вращения. Если бы центр вращения находился на трехмерном объекте, его бы назвали осью .

8.10: Определение поворота – K12 LibreTexts

Преобразования, с помощью которых фигура поворачивается вокруг фиксированной точки для создания изображения.

Обороты

Преобразование – это операция, которая перемещает, переворачивает или иным образом изменяет фигуру для создания новой фигуры. Жесткое преобразование (также известное как преобразование изометрии или преобразование конгруэнтности ) – это преобразование, которое не изменяет размер или форму фигуры.

Жесткие преобразования – это переводы, отражения и вращения . . Новая фигура, созданная преобразованием, называется image .Исходная фигура называется прообраз . Если прообраз \ (A \), то образ будет \ (A ′ \), как сказано «простое число». Если существует образ \ (A ′ \), он будет обозначен как \ (A ′ ′ \), что означает «двойное простое число».

Поворот на – это преобразование, при котором фигура поворачивается вокруг фиксированной точки для создания изображения. Линии, проведенные от прообраза к центру вращения и от центра вращения к изображению, образуют угол поворота .{\ circ} \) о происхождении. Найдите координаты \ (\ Delta A′B′C ′ \).

Рисунок \ (\ PageIndex {11} \)

Решение

Используйте приведенное выше правило, чтобы найти \ (\ Delta A′B′C ′ \).

\ (\ begin {align} A (7,4) & \ rightarrow A ′ (- 7, −4) \\ B (6,1) & \ rightarrow B ′ (- 6, −1) \\ C ( 3,1) & \ rightarrow C ′ (- 3, −1) \ end {align} \)

Дополнительные ресурсы

Видео: Преобразование: Принципы вращения – Основы

Действия: Вопросы для обсуждения по ротации

Учебные пособия: Типы преобразований Учебное пособие

Практика: определение вращения

Реальный мир: радикальные вращения

правил ротации | Обзор геометрии [видео]

Здравствуйте, и добро пожаловать в видео о вращении! В этом видео мы рассмотрим вращение фигуры вокруг точки.Давайте узнаем о ротации!

Вращения везде, куда ни глянь. Земля – ​​наиболее распространенный пример вращения вокруг оси. Колесо автомобиля или велосипеда вращается вокруг центрального болта. Эти два примера вращаются на 360 °. Существуют и другие формы вращения, которые меньше полного вращения на 360 °, например, вращение персонажа или объекта в видеоигре. Говоря более формально, вращение – это форма преобразования, которая поворачивает фигуру вокруг точки. Мы называем эту точку центром вращения .Фигура и ее вращение сохраняют ту же форму и размер, но смотрят в другом направлении. Фигуру можно вращать по часовой стрелке или против часовой стрелки. Еще один отличный пример вращения в реальной жизни – колесо обозрения, в котором центральная ступица является центром вращения.

Мера, на которую поворачивается фигура относительно центра вращения, называется углом поворота . Угол поворота обычно измеряется в градусах. Мы указываем градус и направление вращения.Вот фигура, повернутая на 90 ° по часовой стрелке и против часовой стрелки вокруг центральной точки.

Отличный математический инструмент, который мы используем для отображения поворотов, – это координатная сетка. Начнем с поворота точки вокруг центра (0,0). Если вы возьмете координатную сетку и нанесете точку, а затем поверните бумагу на 90 ° или 180 ° по часовой стрелке или против часовой стрелки относительно начала координат, вы можете найти местоположение повернутой точки. Давайте посмотрим на реальный пример, здесь мы нарисовали точку A в точке (5,6), затем мы повернули бумагу на 90 ° по часовой стрелке, чтобы создать точку A ’, которая находится в точке (6, -5).

Вот та же точка A в точке (5,6), повернутая на 180 ° против часовой стрелки вокруг начала координат, чтобы получить A ’(- 5, -6).

Давайте подробнее рассмотрим два поворота из нашего эксперимента. В нашем первом эксперименте, когда мы поворачиваем точку A (5,6) на 90 ° по часовой стрелке вокруг начала координат, чтобы создать точку A ‘(6, -5), значение y точки A стало значением x точки A’ и значение x точки A стало значением y точки A ‘, но с противоположным знаком.

В нашем втором эксперименте точка A (5,6) повернута на 180 ° против часовой стрелки вокруг начала координат, чтобы создать A ‘(-5, -6), где значения x и y такие же, как у точки A, но с противоположные знаки.

К счастью для нас, эти эксперименты позволили математикам придумать правила для наиболее распространенных поворотов координатной сетки, приняв начало координат (0,0) за центр вращения. Вот правила вращения:

  • Поворот на 90 ° по часовой стрелке: (x, y) становится (y, -x)
  • Поворот на 90 ° против часовой стрелки: (x, y) становится (y, x)
  • 180 ° по часовой стрелке и вращение против часовой стрелки: (x, y) становится (-x, -y)
  • вращение на 270 ° по часовой стрелке: (x, y) становится (-y, x)
  • вращение против часовой стрелки на 270 °: (x, y) становится (y , -x)

Как видите, наши два эксперимента следуют этим правилам.

Теперь, когда мы знаем, как вращать точку, давайте посмотрим на вращение фигуры на координатной сетке. Чтобы повернуть треугольник ABC вокруг начала координат на 90 ° по часовой стрелке, мы должны следовать правилу (x, y) → (y, -x), где значение y исходной точки становится новым значением x, а значение x точки исходная точка становится новым значением y с противоположным знаком. Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C ‘:

  • A (-4, 7) становится A’ (7, 4)
  • B (-6, 1) становится B ‘( 1, 6)
  • C (-2, 1) становится C ‘(1, 2)

Давайте посмотрим на другой поворот.Давайте повернем треугольник ABC на 180 ° вокруг начала координат против часовой стрелки, хотя при повороте фигуры на 180 ° по и против часовой стрелки используется то же правило: (x, y) становится (-x, -y), где координаты вершин повернутый треугольник – это координаты исходного треугольника с противоположным знаком. Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C ‘:

  • A (2,7) становится A’ (-2, -7)
  • B (2,1) становится B ‘( -2, -1)
  • C (6,1) превращается в C ‘(-6, -1)

Вот четырехугольник ABCD.Чтобы повернуть четырехугольник ABCD на 90 ° против часовой стрелки вокруг начала координат, мы будем использовать правило (x, y) становится (-y, x). Давайте применим правила к вершинам, чтобы создать четырехугольник A’B’C’D ‘:

  • A (-8, -2) становится A’ (2, -8)
  • B (-7, -7) становится B ‘(7, -7)
  • C (-2, -6) становится C’ (6, -2)
  • D (-3, -2) становится D ‘(2, -3)

Сейчас Я хочу, чтобы вы сами попробовали несколько практических задач. Кайт KLMN отображается на координатной сетке. Воздушный змей был повернут относительно исходной точки, чтобы создать кайт K’L’M’N ’.Можете ли вы определить, какое вращение воздушного змея KLMN создал воздушный змей K’L’M’N ’?

Начнем с определения координат вершин воздушного змея KLMN и нашего повернутого воздушного змея:

  • K (-8,3) становится K ‘(8, -3)
  • L (-5,5) становится L ‘(5, -5)
  • M (-2,3) становится M’ (2, -3)
  • N (-5, -3) становится N ‘(5,3)

При более внимательном рассмотрении Координаты вершин показывают, что координаты K’L’M’N ‘такие же, как вершины исходного змея, но с противоположным знаком.Давайте посмотрим на правила, единственное правило, при котором значения x и y не меняются, но их знак меняет знак, – это поворот на 180 °.

  • Поворот на 90 ° по часовой стрелке: (x, y) становится (y, -x)
  • Поворот на 90 ° против часовой стрелки: (x, y) становится (-y, x)
  • Поворот на 180 ° по часовой стрелке и вращение против часовой стрелки: (x , y) становится (-x, -y)
  • вращение на 270 ° по часовой стрелке: (x, y) становится (-y, x)
  • поворот на 270 ° против часовой стрелки: (x, y) становится (y, -x)

Следовательно, воздушный змей KLMN был повернут на 180 ° относительно исходной точки для создания воздушного змея K’L’M’N ‘.

Давайте посмотрим на другую проблему. Пентагон QRSTU показан на координатной сетке. Поверните пятиугольник QRSTU на 90 ° против часовой стрелки, чтобы создать пятиугольник Q’R’S’T’U ’.

Давайте начнем с определения координат вершин нашего исходного пятиугольника. Правило для поворота на 90 ° против часовой стрелки: (x, y) становится (-y, x), давайте применим правило, чтобы найти вершины нашего нового пятиугольника.

(x, y) становится (-y, x)

  • Q (-6,6) становится Q ‘(-6, -6)
  • R (-4,7) становится R’ (-7, -4)
  • S (0,4) становится S ‘(-4,0)
  • T (-4,1) становится T’ (-1, -4)
  • U (-6,2) становится U ‘(-2, -6)

Теперь нанесем точки на координатную сетку и пометим вершины.

Последняя практическая проблема. Трапеция PQRS, где P (-3, -5), Q (3, -5), R (5, -2) и S (-5, -2) повернута на 90 ° по часовой стрелке вокруг начала координат для создания трапеции P. ‘Q’R’S’. Создайте обе трапеции на координатной сетке.

Мы начнем с решения, какое правило использовать для поворота на 90 ° по часовой стрелке относительно начала координат. Мы собираемся использовать (x, y) становится (y, -x). Теперь применим правило к координатам вершин PQRS.

  • P (-3, -5) становится P ‘(-5,3)
  • Q (3, -5) становится Q’ (-5, -3)
  • R (5, -2) становится R ‘(-2, -5)
  • S (-5, -2) становится S’ (-2,5)

Теперь давайте нарисуем точки и создадим трапеции на координатной сетке.

Надеюсь, что этот обзор ротации был вам полезен! Спасибо за просмотр и удачной учебы!

Вращение – фигура, симметрия, центр и вращение

Вращение – это одно из трех жестких движений, которые перемещают фигуру в плоскости без изменения ее размера или формы. Как следует из названия, вращение перемещает фигуру, вращая ее вокруг центра где-нибудь на плоскости. Этот центр может быть где-то внутри или на фигуре, или полностью вне фигуры. Два других жестких движения – это отражений и переводов .

На рисунке 1 показано вращение на 30 ° вокруг точки C. Это вращение против часовой стрелки, что считается положительным. Вращение по часовой стрелке составляет минус . «Произведение» двух вращений, то есть после одного вращения Рисунок 1. Иллюстрация Hans & Cassidy. Предоставлено Gale Group. с другим, тоже вращение. Это предполагает, что центр вращения одинаков для обоих. Когда кто-то перемещает тяжелую коробку по комнате, вращая ее сначала в одном углу, а затем в другом, этот «продукт» не является вращением.

Вращения настолько обычны, что легко забыть, насколько они важны. Человек ориентирует карту, вращая ее. Часы показывают время время вращением стрелок. Человек вставляет ключ в замок , поворачивая ключ до тех пор, пока его пазы не совпадут с рисунком замочной скважины. Поворот M на 180 ° превращает его в W; 6 и 9 похожи, за исключением вращения.

Вращательные движения – это одно из двух основных движений деталей в машине. Колесо автомобиля преобразует вращательное движение в поступательное движение и приводит в движение автомобиль.Сверло просверливает отверстие, отрезая материал по мере его вращения. Земля вращается вокруг своей оси. Земля и луна вращаются вокруг своих центров тяжести и так далее.

Астрономия до Коперника была очень сложной из-за попытки использовать Землю в качестве центра вращения планет. Когда Кеплер и Коперник сделали Солнце Солнце гравитационным центром, движения планет стало намного легче предсказать и объяснить (но даже с Солнцем в качестве центра движение планет не является строго вращательным).

Когда точки представлены координатами, вращение может выполняться алгебраически. Насколько сложно это сделать, зависит от местоположения центра вращения и от типа используемой системы координат. В двух наиболее часто используемых системах, прямоугольной декартовой системе координат и полярной системе координат, центром выбора является начало координат или полюс.

В любой из этих систем вращение можно рассматривать как перемещение точек и оставление осей фиксированными, или Рисунок 2. Иллюстрация Ганса и Кэссиди. Предоставлено Gale Group. наоборот. Математическая связь между этими альтернативами проста: вращение набора точек по часовой стрелке эквивалентно вращению осей, особенно с отражениями, обычно предпочтительно оставлять оси на месте и перемещать точки.

Когда точка или набор точек представлены с полярными координатами , уравнения, связывающие точку (r, θ) с повернутым изображением (r ‘, θ’), особенно просты.Если θ 1 – это угол поворота :

Таким образом, если точки повернуть на 30 ° против часовой стрелки, (7,80 °) будет изображение 7,50 °). Если множество точек, описываемых уравнением r = θ / 2, повернуть на π единиц по часовой стрелке, его изображение описывается как r = θ – π) / 2. Прямоугольные координаты связаны с полярными координатами уравнениями x = r cos θ и y = r sin θ.

Следовательно, уравнения, связывающие точку (x, y) с ее повернутым изображением (x ‘, y’), следующие:

Используя тригонометрические тождества для cos (θ + θ 1 ) и sin (θ + θ 1 ), можно записать x ‘= x cos θ 1 – y sin θ 1 и y ‘= x sin θ 1 + y cos θ 1 или, после решения относительно x и y: x = x’ cos θ 1 + y sin θ 1 и y = -x ‘sin θ 1 + y cos θ 1 .

Чтобы использовать эти уравнения, необходимо обратиться к таблице синусов и косинусов или использовать калькулятор с ключами SIN и COS.

Уравнения вращения можно использовать по-разному. Одно из применений – упростить уравнение, такое как x 2 – xy + y 2 = 5. Для любого полиномиального уравнения второй степени по x и y существует вращение, которое устраняет член xy . В этом случае поворот составляет 45 °, и в результате получается уравнение после отбрасывания простых чисел: 3x 2 + y 2 = 10.

Другая область, в которой вращение играет важную роль, – это вращательная симметрия . Фигура имеет вращательную симметрию, если есть поворот, при котором исходная фигура и ее изображение совпадают. Квадрат, например, обладает симметрией вращения, потому что любое вращение вокруг центра квадрата, кратное 90 °, приведет к тому, что квадрат будет совпадать с оригиналом. Обычная шестерня имеет вращательную симметрию. То же самое и с многочисленными предметами, такими как вазы и миски, которые неоднократно украшены по краям.Фактические объекты можно проверить на симметрию вращения, посмотрев на них. Аналитически описанные геометрические фигуры можно проверить с помощью уравнений вращения. Например, спираль r = 28 имеет двойную вращательную симметрию. При повороте спирали на 180 ° изображение совпадает с исходной спиралью.


Книги

Coxeter, H.S.M. и S. L. Greitzer. Возвращение к геометрии. Вашингтон, округ Колумбия: Математическая ассоциация Америки, 1967.

Гильберт Д. и С. Кон-Фоссен. Геометрия и воображение. Нью-Йорк: Chelsea Publishing Co., 1952 г.

Петтофреццо, Энтони. Матрицы и преобразования. Нью-Йорк: Dover Publications, 1966.

Яглом И.М. Геометрические преобразования. Вашингтон, округ Колумбия: Математическая ассоциация Америки, 1962.


Заполните пропуски Рисунок Центр вращения Класс порядка 9 математика CBSE

Подсказка: Мы возьмем каждую форму всех диаграмм и повернем их под подходящими углами и найдем угол симметрии и порядок симметрии.\ circ $

Примечание: Прежде чем переходить к этой задаче, нам нужно знать некую базовую концепцию, которая называется «вращательной симметрией».
Вращательная симметрия формы объясняет, что когда объект вращается вокруг собственной оси, форма объекта выглядит так же.
Центр вращения для объекта, имеющего симметрию вращения, – это фиксированная точка, вокруг которой происходит вращение, называемая центром вращения.
Порядок вращательной симметрии для объекта, имеющего вращательную симметрию, – это количество позиций, в которых фигура может быть повернута и по-прежнему выглядит точно так же, как и до поворота.
Угол вращательной симметрии для объекта, имеющего вращательную симметрию, – это угол поворота во время вращения, называется углом поворота.

Команда: cofr

Команда: cofr

Команда: cofr

Использование:


cofr [ frontCenter | centerOfView | фиксированный ] [ showPivot true | ложь | длина, радиус ]

Использование:


~ cofr

Использование:


cofr [ spec | x, y, z ] [ Система координат модель-спецификация ] [ showPivot true | ложь | длина, радиус ]

Команда cofr устанавливает центр вращения и / или изменяет его рассчитывается.Если аргументы не указаны, cofr сообщает текущий центр вращения и метод расчета в журнале Log . Смотрите также: вид , режим мыши , центр измерения

Первый набор опций определяет метод центра вращения :

  • frontCenter – используйте метод переднего центра (также указывается с ~ cofr ): когда вид уменьшен, использовать центр ограничивающей рамки всех отображаемых элементов; когда вид увеличен, продолжайте обновлять центр вращения до середина графического окна по осям X и Y (координаты экрана) и глубина самого переднего отображаемого элемента в этой точке, или, если середина пуста, сохраняя глубину той же, пока другой элемент проходит через эту точку.Центр вращения обновляется только для перемещений, а не только для вращений.
  • centerOfView – продолжайте обновлять центр вращения до середина графического окна по осям X и Y (координаты экрана), с Z (глубина) на полпути между ближней и дальней плоскостями отсечения. Если активна только одна из ближних / дальних плоскостей, глубина центра вращения отслеживает активную плоскость. Если ни одна из плоскостей отсечения не активна, глубина центра вращения остается постоянной, начиная с центра ограничивающая рамка первой модели открыта, или, если метод был переключен, от предыдущего центра вращения.
  • fixed – использовать фиксированную точку относительно сцена; предоставление этой опции изменяет только метод, сохраняя текущий центр

Остальные параметры определяют конкретный фиксированный центр вращения . Если дана спецификация , центр вращения будет установлен в центр ограничивающей рамки указанных элементов (только отображаемые части). В качестве альтернативы центр можно ввести как координаты x, y, z . Система координат может быть указана по номеру ссылочной модели.В противном случае система координат сцены будет использоваться.

Опция showPivot переключает отображение перекрестия изображения центр вращения или регулирует длину и радиус прицела осевые цилиндры. Начальная длина и радиус цилиндра по умолчанию: 2 и 0,05 в единицах координат данных, обычно Å. Красная, зеленая и синяя оси выровнены по осям X, Y и Z в система координат сцены.

Ресурс UCSF для биокомпьютеров, визуализации и информатики / Ноябрь 2019

Центр тяжести, центр вращения, точка вращения

PDF ФАЙЛ – НАЖМИТЕ ЗДЕСЬ ДЛЯ ПЕЧАТИ РАБОЧЕГО ЛИСТА

Обычно центр тяжести объекта понимается как центр распределения веса объекта.Это означает что если объект может вращаться вокруг своего центра тяжести, он уравновесит в таком случае.

Обувь акробата приклеена к платформе. Вес акробата и вес противовеса равны. Это означает, что центр силы тяжести (также центр вращения) можно найти в центре тяжести распределение.
Если акробат наклоняется вправо, вся платформа и балансировка вес будет вращаться, пока не будет балансировать вокруг своего центра тяжести / центра вращения.
Вся конструкция окажется в горизонтальном положении, потому что левую и правую стороны, взвесьте одинаково и сбалансируйте.
При увеличении балансировочного веса центр вращения и центр тяжести перемещаются в новую «балансировку» позиция.Однако, если балансировочный груз, акробат и платформа не вынужден вращаться вокруг большого стального болта, в фиксированном положении он можно гарантировать, что вес всегда будет ниже акробата. Этот потому что вес тяжелее, чем у акробата, и центр гравитация ниже фиксированного центра вращения.

Точка, в которой вращение акробата, платформы и веса теперь называется “фиксированной точкой вращение ». Это не центр тяжести.

ПОИСК ЦЕНТРА ВЕС
Центр тяжести объекта может быть найти довольно легко. Кусок веревки с грузом на конце (называемый отвес), подвешивается к любой точке на краю объекта.А канцелярская булавка может использоваться, чтобы удерживать веревку на месте. Вертикальная линия нарисуйте, выровняв по нитке. Затем объект немного поворачивается, и последовала та же процедура. В месте пересечения линий находится центр тяжести. Повторите процедуру в третий раз, чтобы подтвердить положение центра. гравитации.
Птица, изображенная ниже, является частью балансирующая игрушка. Если центр тяжести найден и используется как центр вращения, игрушка должна уравновеситься.

С балансировочными игрушками этого типа, часто рекомендуется располагать центр тяжести немного ниже положение стального стержня (фиксированный центр вращения).

НАЖМИТЕ ЗДЕСЬ, чтобы СИЛЫ И МОМЕНТЫ УКАЗАТЕЛЬ СТР.

Автор: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

×