Физика для всех: лекции в ноябре
В рамках цикла открытых научно-популярных лекций в ноябре пройдут встречи:
5 ноября – 16:00–18:00 – Лекция с демонстрацией опытов «От палеолита до игрушки для кота»
«Палеолит»: физика в технологиях каменных орудий.
«Игрушка для кота»: несколько опытов с лазером и бытовыми предметами, например, дифракция на морском ёжике.
Лекцию читает Дмитрий Андреевич Лисаченко (преподаватель Академической гимназии имени Д. К. Фаддеева СПбГУ)
12 ноября – 16:00–17:30 – Лекция «Подобие в природе: проблемы Гулливера в стране лилипутов»
Мы поговорим о том, каким образом меняются физические законы на разных масштабах расстояний, а также о следствиях этих изменений в живой и неживой природе:
- зачем слону толстые ноги, а пингвину – короткие,
- почему все деревья примерно одной высоты, и похожи на свои ветки, а ветки — на листья,
- каковы перспективы горнолыжного спорта на Марсе,
- как определить мощность ядерного взрыва по фотографии.
Лекцию читает Антон Андреевич Шейкин, кандидат физико-математических наук (старший преподаватель, кафедра физики высоких энергий и элементарных частиц СПбГУ)
19 ноября – 16:00–19:00 – Лекция с демонстрацией опытов «Гидростатика. Свойства воды»
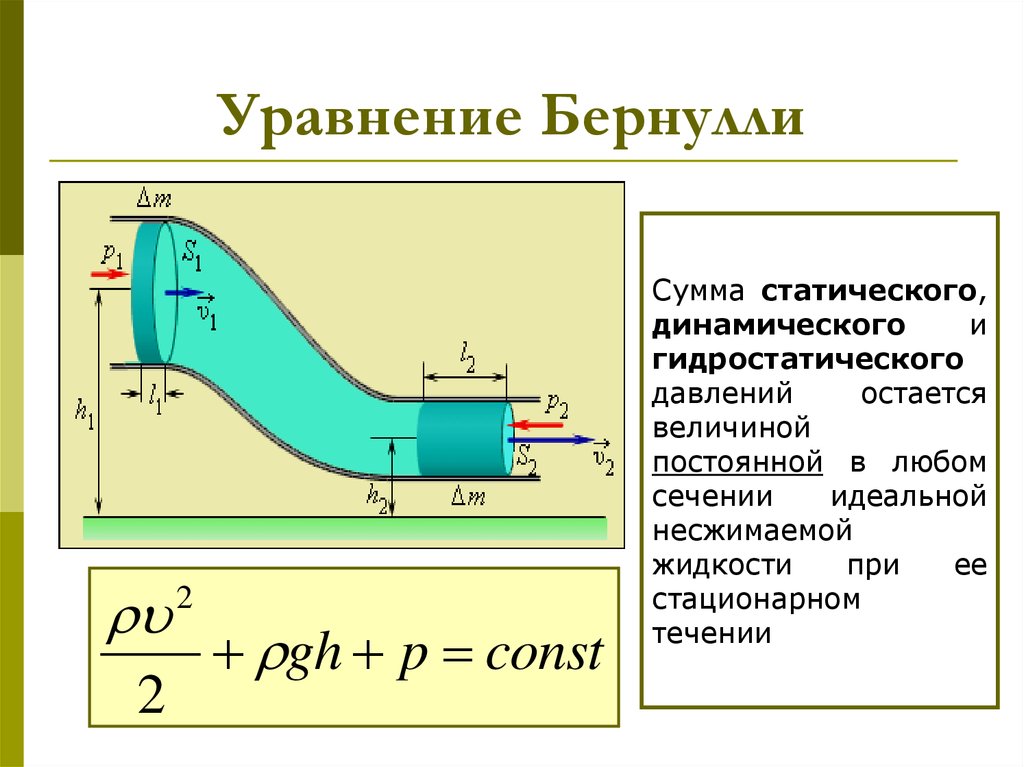
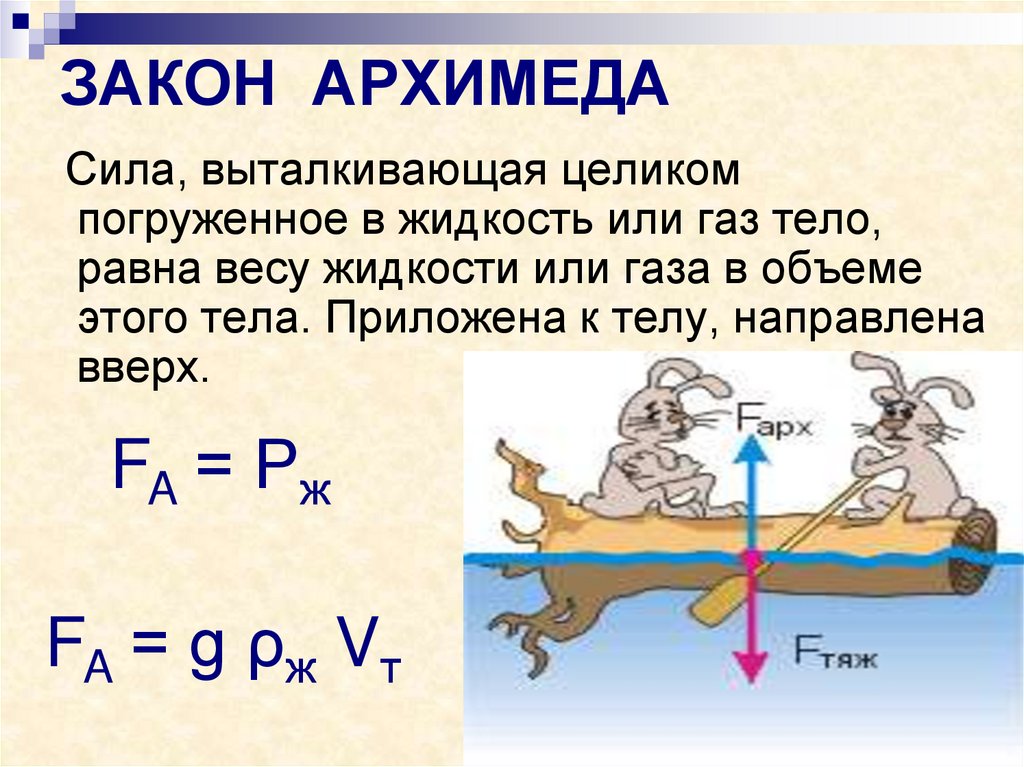
Речь пойдет о равновесии в жидкостях и газах, а также о распределении давления в них. Среди первых создателей теоретической статики был древнегреческий ученый Архимед, который сформулировал основной закон гидростатики. На лекции мы обсудим многие свойства жидкостей, в первую очередь, воды, но также и некоторых других.
Лекция включает в себя:
- исследование свойств жидкостей и газов;
- разбор исторических экспериментов, таких как задача Архимеда и гидростатический парадокс;
- вывод основного уравнения гидростатики; изучение явления вакуума;
- условие плавания тел в различных средах с многочисленными примерами из реальной техники.
Вы узнаете, почему огромные корабли не тонут, а монета сразу идет на дно, как устроены подводные лодки, гидравлические машины, гидроуровень и, наконец, вместе соберем фонтан.
Лекцию читают Илья Владимирович Блашков (кафедра фотоники, ведущий инженер УТООП) и Никита Александрович Зайцев (кафедра физики атмосферы, инженер РЦ «Геомодель» Научного парка СПбГУ)
26 ноября – 16:00–17:30 – Лекция «Моя первая олимпиада по физике. Тепловые явления»
На занятии подготовимся к участию в олимпиадах по физике. Проведем разбор задач уровня Санкт-Петербургской Открытой городской олимпиады по физике для 7–8 классов на темы: тепловое равновесие, нагревание, плавление, испарение, работа с графиками.
Лекцию читает Анна Петровна Горбенко (доцент СПбГУ, кафедра общей физики-1)
Трансляция проводится на платформе ВКонтакте в группе «Физика для всех! | СПбГУ».
Чтобы получить приглашение на мероприятие, необходимо стать участником группы «Лабораторная экспериментальная площадка | Физика» и заполнить анкету «Физика для всех».
Страница не найдена
К сожалению, такой страницы на сайте больше нет. Попробуйте воспользоваться картой сайта.
Каталог товаров
|
Основные разделы
|
2
гидродинамика – Поддерживает ли вода одинаковый уровень в соединенных сосудах?
спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 43к раз
$\begingroup$
Рассмотрим систему, показанную ниже:
Две бочки по 55 галлонов используются для хранения воды, стекающей по желобу.
Эти бочки соединены друг с другом на дне, чтобы поддерживать между ними одинаковый уровень воды.
Они питаются от вертикальной трубы диаметром 4 дюйма, соединенной с горизонтальной трубой диаметром 2 дюйма.
Когда 4-дюймовая вертикальная труба с одного конца наполнится водой, вода потечет в горизонтальную трубу и начнет заполнять бочки. Будут ли бочки поддерживать тот же уровень, что и в вертикальной трубе диаметром 4 дюйма, при условии, что расход на входе не слишком велик, чтобы перекрыть горизонтальную трубу диаметром 2 дюйма? Другими словами: $h_1 = h_2$ на диаграмме? Я думаю, что так и должно быть, так что, если это правда, какой физический принцип работает, чтобы поддерживать равные уровни, когда диаметр бочки отличается от диаметра трубы?
- гидродинамика
- гидростатика
$\endgroup$
11
$\begingroup$
Да, все уровни будут на одной высоте.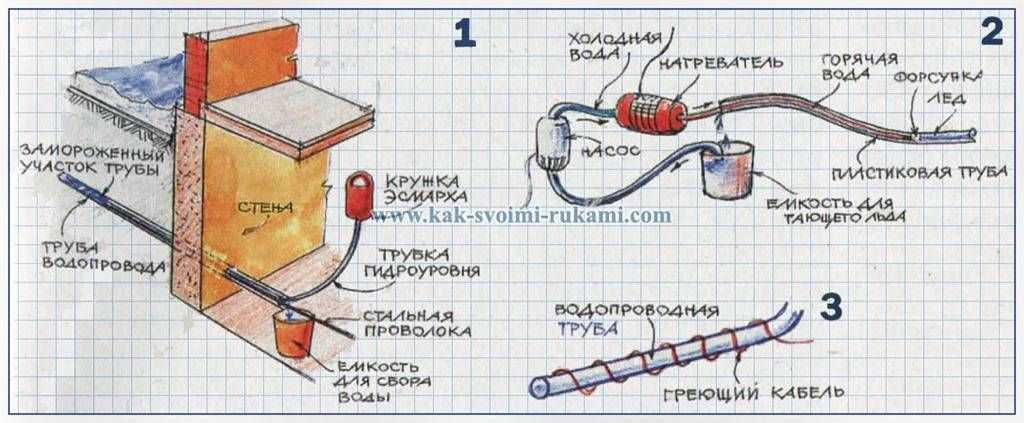
Давление (относительно атмосферного) столба воды, открытого сверху в атмосферу, линейно пропорционально глубине в этой точке от поверхности воды. Грубо говоря, давление повышается примерно на 1 PSI на каждые 2 фута вниз от поверхности. Представьте, если бы в одной бочке было 1 фут воды, а в другой 3 фута. Давление на дне второй бочки будет на 1 PSI выше, чем на дне первой. Это заставит воду течь по горизонтальной трубе из второго в первый.
Единственный способ, при котором эта система является стабильной (вода не течет активно вокруг изменяющихся уровней в бочках), – это когда давление на дне двух бочек одинаково, что означает, что высота воды в каждой бочке равна одинаковый. Все водные поверхности находятся на одной высоте, поэтому все давления везде на одной и той же высоте одинаковы. Когда это не так, вода будет течь, пока это не так.
$\endgroup$
0
$\begingroup$
Если бочки не открыты сверху, воздух внутри создаст барьер, но воздух внутри может быть сжат, поэтому, если вода будет стекать по водосточной трубе, она создаст большее давление на воду, тем самым сжимая воздух в резервуарах.
В какой-то момент силы не хватит для преодоления давления в баке и оно либо уравняет, либо вернет силу обратно вверх по желобу.
$\endgroup$
$\begingroup$
Если бочки запечатаны, нет требования, чтобы уровни были одинаковыми. Они могут быть как ниже, так и выше, в зависимости от давления воздуха в верхней части ствола.
В качестве простой демонстрации наполните ведро водой, опустите в него стакан, а затем поднимите его вверх дном: уровень воды поднимется выше уровня ведра, даже если наверху останется воздух, потому что давление в верхней части стакана намного меньше атмосферного давления.
Для чего-то более экстремального попробуйте следующее:
Источник изображения
$\endgroup$
$\begingroup$
Это происходит потому, что (согласно закону Паскаля о передаче давления в жидкостях) давление в замкнутой несжимаемой жидкости передается одинаково и без уменьшения во всех направлениях по всей жидкости
$\endgroup$
$\begingroup$
Предполагая, что бочки открыты для атмосферного давления, простой и очевидный ответ заключается в том, что уровни должны быть одинаковыми или такими же, как если бы гранулированный материал был помещен в контейнеры – без учета трения, поскольку вес жидкости в более наполненных контейнерах толкает с большей силой, чем другие, и не может оставаться в статическом равновесии, поэтому результат выравнивается (таким образом, это функция массы, а не давления).
$\endgroup$
1
$\begingroup$
Если все 3 открыты для одного и того же атмосферного давления, единственное, что может изменить уровни (временно), — это кинетическая энергия воды, движущейся по соединительным трубам. Он поднимет уровень немного выше в контейнере, к которому движется, и опустит уровень в том, что позади. Как только кинетическая энергия будет израсходована из-за трения и увеличения сопротивления давлению на более высоком уровне, процесс будет обратным, так как теперь более высокий уровень будет течь обратно на более низкий уровень. Этот цикл будет продолжаться некоторое время, пока кинетическая энергия не будет потеряна из-за трения, после чего уровни будут одинаковыми. Подобно маятнику, движущемуся вперед и назад, но маятник будет совершать больше циклов из-за гораздо меньшего трения.
$\endgroup$
$\begingroup$
зависит от размера двух стволов, открытых в атмосферу.
если оба имеют одинаковую размерность, то с помощью уравнения Бернулли оба будут иметь одинаковый уровень воды, иначе
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
optics – Почему уровень воды в трубке наклонен, а не горизонтален, как и уровень воды в остальной части стакана?
В основном это связано с эффектами поверхностного натяжения и постоянным значением угла контакта между водой, воздухом и твердой поверхностью.
Мы можем доказать это, объединив уравнения Юнга-Лапласа с законом Стевино для жидкости. Здесь предполагается, что кривизна свободной поверхности мала, так что ее кривизну можно аппроксимировать производной второго порядка.
Координаты. Я использую здесь 2D-модель, чтобы максимально упростить вычисления. Я ввожу здесь декартову систему отсчета с началом в точке пересечения свободной поверхности и оси трубы, совпадающей с осью $\xi$, направленной вверх, и ортогональной ей $\eta$-осью. Определим угол $\alpha$ как угол между вертикальной осью $z$, направленной вверх, и осью $\xi$. С этими системами отсчета мы можем определить правило преобразования, чтобы получить
$z = \xi \cos\alpha – \eta \sin\alpha$
Свободная поверхность описывается здесь как (неизвестная) функция $\xi_s(\eta)$, которую можно описать с помощью $z$ -координировать как
$z_s(\eta) = \xi_s(\eta) \cos\alpha – \eta \sin\alpha$.
От Юнга-Лапласа и Стевино к ОДУ для формы свободной поверхности. 2D уравнение Юнга-Лапласа для малой кривизны свободной поверхности принимает вид
$\Delta P = \gamma \kappa$ $\qquad \rightarrow \qquad P_{a} – P(\eta) = \gamma \, \xi_s”(\eta)$
$\Delta P$ скачок давления на свободной поверхности, $P_a$ приблизительно равномерное давление в воздухе на свободной поверхности, $P(\eta)$ давление в жидкости на свободной поверхности, $\каппа \sim \xi_s”(\eta)$ кривизна свободной поверхности.
Теперь мы можем использовать закон Стевино, чтобы явно записать давление в жидкости $P(z) = P_0 – \rho g z$, где $P_0$ давление в жидкости на высоте начала системы отсчета $0 $, для которых $\xi=0$, $\eta=0$ и, следовательно, $z=0$. Используя преобразование координат $z(\xi,\eta)$, мы можем записать давление на свободной поверхности как 9{nd}$ заказать ОДУ и найти неизвестное значение давления $P_0$. Эти условия таковы:
- свободная поверхность, проходящая через начало координат, для нашего выбора системы отсчета:
- $\eta_s(0) = 0$
- угол контакта и, следовательно, поверхностная производная у твердых стенок:
- $\eta_s'(-\ell/2) = -\theta$
- $\eta_s'(\ell/2) = \theta$
Решение ОДУ.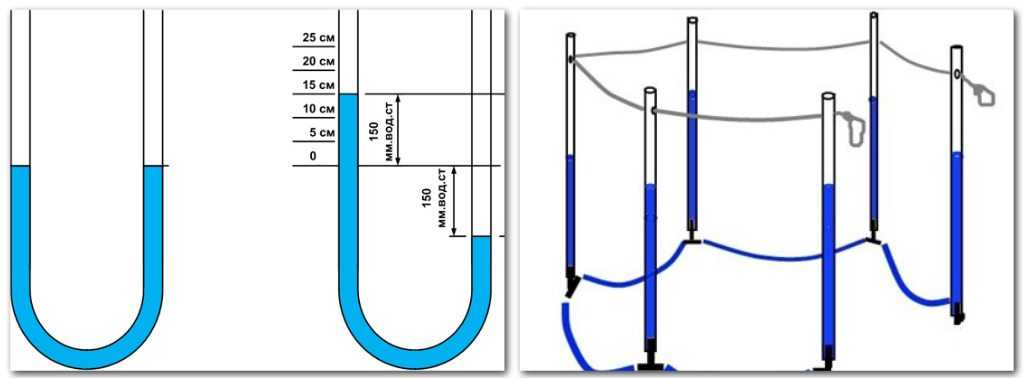
Решение линейного ОДУ находится как сумма частного решения и решения однородного уравнения
$\xi_s(\eta) = A \cosh(c \eta) + B \sinh(c \eta) + \eta \tan\alpha + \dfrac{P_a – P_0}{\rho g \cos\alpha }$,
определив константу $c = \sqrt{\frac{\rho g}{\gamma}}$ Эта константа имеет физическую размерность $\dfrac{1}{\text{length}}$, поэтому что его можно интерпретировать как характерную длину явления капиллярности. Значение констант $A$, $B$ и давление $P_0$ оцениваются, задавая 3 граничных условия, чтобы получить
$A = \dfrac{\theta}{c \sinh ( c \ell/2) }$
$B = -\dfrac{\tan\alpha}{c \cosh(c \ell/2)} $
$P_0 = P_a + \rho g A \cos \alpha$,
и решение
$ \xi_s(\eta) = A \left[ \cosh\alpha – 1 \right] + B \sinh(c \eta) + \eta \tan \alpha$.
Теперь мы можем записать решения, используя координату $z_s(\eta)$, как
$z_s(\eta) = \xi_s(\eta) \cos\alpha – \eta \sin\alpha = $
$\ qquad = A \left[ \cosh(c \eta) – 1 \right] \cos\alpha + B \sinh(c \eta) \cos\alpha +\eta\sin\alpha – \eta\sin\alpha = $
$\qquad = A \left[ \cosh(c \eta) – 1 \right] \cos\alpha + B \sinh(c \eta) \cos\alpha $.
