РАСЧЕТ МОЩНОСТИ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ ПРИВОДА КОМПРЕССОРА
При выборе мощности двигателя для компрессора, как и для всех механизмов с продолжительным режимом работы и постоянной нагрузкой, требуемую мощность Рдв двигателя находят по мощности на валу механизма с учётом потерь в промежуточном звене механической передачи.
В зависимости от назначения, мощности и характера производства, где установлены механизмы этой группы, они могут требовать или небольшого, но постоянного подрегулирования производительности при отклонении параметров воздуха от заданных значений, или же регулирования производительности в широких пределах.
Мощность двигателя компрессора определяется по формуле:
где: Q – производительность (подача) компрессора, м3/с; А=(Аи+Аа)/2 –работа, Дж/м3, изотермического и адиабатического сжатия 1 м3 атмосферного воздуха давлением ρ1 = 1,01·105 Па до требуемого, давления ρ2, Па; для давлений до 10·105 Па значения А указаны ниже:
ηк – индикаторный КПД компрессора, учитывающий потери мощности при реальном процессе сжатия воздуха и равный 0,6 – 0,8;
ηп – КПД механической передачи между компрессором и двигателем, его значения лежат в пределах 0,9 – 0,95;
k3 – коэффициент запаса, равный 1,05 – 1,15 и учитывающий не поддающиеся расчету факторы.
Таким образом, расчетная мощность двигателя равна:
Из литературы [7] (табл. 11.6, с. 269) выбираем двигатель СТД – 1600 – 2УХЛ4, напряжением 10 кВ, с частотой вращения 3000 об/мин.
СТД – синхронный турбодвигатель;
1600 – мощность двигателя, кВт;
2 – число полюсов;
УХЛ4 – климатическое исполнение и категория места размещения.
Для компрессора типичен продолжительный режим работы, поэтому их электроприводы, как правило, нереверсивные с редкими пусками. Также компрессор имеет небольшие пусковые статические моменты – до 20-25% от номинального.
Выбор синхронного двигателя обуславливается несколькими основными причинами:
Во-первых, это жёсткая характеристика синхронных двигателей, то есть при увеличении нагрузки на валу двигателя обороты не изменяются, что очень важно для производительности компрессора.
Во-вторых, при своих габаритах синхронный двигатель имеет гораздо большую мощность по сравнению с асинхронным двигателем.
В-третьих, синхронный двигатель имеют К. П.Д. на 2,5% больше (96,6%), чем у асинхронных двигателей и момент имеет прямо пропорциональную зависимость от напряжения.
П.Д. на 2,5% больше (96,6%), чем у асинхронных двигателей и момент имеет прямо пропорциональную зависимость от напряжения.
Производительность компрессоров можно изменять тремя способами: изменением угловой скорости приводного двигателя, изменением сопротивления магистрали (трубопровода) с помощью задвижки, а также конструктивными изменениями рабочих органов механизма в процессе регулирования.
В-четвёртых, у синхронных двигателей при номинальном токе cosφ = l, а при перевозбуждении двигатель может служить в качестве компенсатора реактивной мощности и повышать cosφ предприятия в целом.
Расчет компрессора:
Необходимо построить цикл в тепловой диаграмме lgPi для Ф-22. Для этого рассчитываются необходимые параметры для построения цикла.
Холодильная машина работает на Ф-22 с перегревом на всасывании и переохлаждением перед РВ.
Для
воздушного способа охлаждения помещения t0=tn-(18÷120)=25-15=10(0С), где tn –температура
воздуха помещения.
Перегрев паров фреона перед всасыванием находится в пределах 10÷28
tвс=t0+∆tпер.= 10+(10÷200)=10+12=22(0С).
Температура конденсации tк и tn
Таким образом tк=tн.в.+(10÷200)=30+(10÷200)=45(0С),
tп=tн.в.+(5÷15)0=30+(5÷150)=40(0С)
По
рассчитанным температурам строится
цикл холодильной машины в диаграмме lgPi и определяются параметры
узловых точек. Параметры заносятся в
таблицу и используются для дальнейшего
расчёта.
Таблица №3
№
t 0
Р
бар
Р
МПа
i кДж/кг
v м3/кг
1‘
10
11
1,1
417
1,72
1
23
11
1,1
430
0,024
2′
28
2,8
419
0,0075
2
70
28
2,8
458
0,011
3
22
28
2,8
280
3‘
45
28
2,8
268
4
10
11
1,1
268
При расчете определяем
Удельную холодопроизводительность, кДж/кг,
==417-268=149(кДж/кг).
Объемную производительность, кДж/м3,
( кДж/м3)
где- объём всасываемых паров компрессором.
Из формулы Q0=Gа·q0 можно определить массовый расход циркулирующего в машине хладагента кг/с Ga=Q
По формуле Qv=Qo/v1=18/1,72=10,47 (м3/ с) можно рассчитать объемную производительность компрессора м3/ с.
Работа, затрачиваемая на сжатие 1 кг хладагента считается по формуле: ,кДж/кг.
Считаем действительный холодильный коэффициент эффективности работы холодильной машины .
 В случае работы холодильной машины по
циклу теплового насоса (нагрев воздуха),
эффективность работы оценивается
тепловым коэффициентом, учитывающим
потери в прямом и обратном цикле
холодильной машины. Этот коэффициент
можно посчитать по формуле
В случае работы холодильной машины по
циклу теплового насоса (нагрев воздуха),
эффективность работы оценивается
тепловым коэффициентом, учитывающим
потери в прямом и обратном цикле
холодильной машины. Этот коэффициент
можно посчитать по формуле
Для расчета мощности компрессора холодильной машины надо учитывать все энергетические и объемные потери мощности действительного цикла холодильной машины. Эти потери учитываются коэффициентом подачи и учитывают степень заполнения рабочего объема цилиндров, всасываемых паром хладагента ;
а) – объемный или индикаторный коэффициент, учитывающий объемные потери от наличия мертвого пространства и сопротивление в клапанах.
где С – отношение мертвого пространства к объему цилиндра:
для фреоновых компрессоров С = 0,03 ÷0,04;
б) – коэффициент подогрева, учитывающий объемные потери от теплообмена в цилиндре,
, Т=(273 + t oC) – в градусах Кельвина;
в) – коэффициент, учитывающий неплотности в цилиндре; зависит от конструкции и степени износа компрессора,
.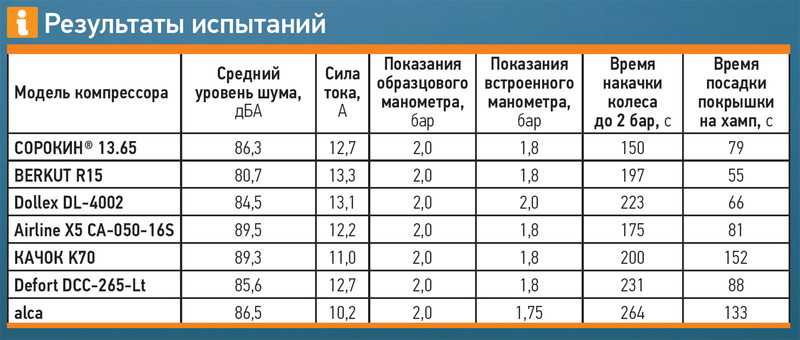
Действительный объём, описываемый поршнем компрессора, м3/с
.
По найденному объему можно по каталогу подобрать марку компрессора, объемная подача которых, должна быть на 20÷40 % больше требуемой мощности привода компрессора :
Определяем теоретическую (адиабатическую) мощность сжатия: , (кВт)
Определяем действительную мощность сжатия, кВт (кВт), где – индикаторный коэффициент для малых компрессоров – (0,7÷0,8)
Мощность на валу компрессора (эффективная мощность кВт) (кВт), где – для современных малых компрессоров 0,9.
Электрическая мощность, т.е. мощность потребляемая электродвигателем компрессора, кВт: (кВт), для малых компрессоров =0,85÷0,9.
С
учётом найденной объемной производительности,
мощности двигателя компрессора и работы
компрессора на хладагенте R410B
по каталогу либо справочнику подбирается
компрессор для холодильной машины.
Расчет мощности центробежного компрессора
Рифка Айсия Компрессор
В этом посте я хочу поделиться с вами, как рассчитать мощность центробежного компрессора так как его ищут очень многие технологи (а я тоже не знаю как).
Для расчета мощности центробежного компрессора нам потребуются следующие свойства газа: коэффициент сжимаемости (Z), молекулярная масса (MW), температура газа на входе, давление газа на входе, давление газа на выходе, адиабатическая составляющая (Cp/Cv) и массовый расход .
Давайте начнем с примера, а я покажу вам шаг за шагом метод расчета. В этом примере у нас есть эти свойства газа (я использую единицы США).
Compressibility factor (Z) = 0.9972
Molecular weight (MW) = 18. 15
15
Gas constant (R) = 1544/molecular weight
Inlet temperature (T1 ) = 546 градусов R
Давление на входе (P1) = 15 psia (don’t forget to use absolute pressure)
Outlet pressure (P2) = 60 psia
K (Cp/Cv) = 1,274
Расход (Вт) = 0,184 фунт/мин
Необходимые данные для расчета мощности центробежного компрессора: напор . Мы можем использовать либо адиабатический напор, либо политропический напор, если мы используем вместе адиабатический КПД и политропический КПД.
В этом примере мы рассчитаем требуемую мощность с использованием адиабатического напора, политропического напора и симулятора процесса. Мы хотим знать, дают ли эти методы одинаковые результаты или нет.
Расчет мощности центробежного компрессора с использованием адиабатического напора Для расчета адиабатического напора и мощности мы используем приведенное ниже уравнение.
Из приведенных выше данных адиабатический напор ( Had ) равен 74 808,54 фут-фунт-сила/фунт-м .
Для расчета мощности нам потребуется адиабатический КПД (Еа) . Адиабатический КПД зависит от типа компрессора, оборотов в минуту, объемного расхода и адиабатического напора. Мы можем определить адиабатический КПД, используя рисунок ниже.
Адиабатический КПДНа приведенном выше рисунке показано, что для центробежного компрессора адиабатический КПД находится в диапазоне от 60% до 80%. Для предварительного расчета выбираем 70% адиабатический КПД.
Используя второе уравнение, мы получаем требуемую мощность 0,594 л.с. .
Расчет мощности центробежного компрессора с использованием политропного напора Для расчета мощности с использованием политропного напора нам нужно политропный КПД . Политропический КПД является функцией адиабатического КПД. Соотношение между этими показателями эффективности выражено в уравнении ниже.
Политропический КПД является функцией адиабатического КПД. Соотношение между этими показателями эффективности выражено в уравнении ниже.
Из приведенного выше уравнения мы получаем политропную эффективность 73,99% . Обратите внимание, что вы можете заменить (N-1)/N на (K-1)/KEp.
Для расчета политропного напора и мощности с использованием политропных данных используйте приведенное ниже уравнение.
Расчет мощности центробежного компрессора с использованием политропного напораИспользуя уравнение, мы получаем политропный напор: 79 075,11 ft lbf/lbm . Требуемая мощность составляет 0,594 л.с. , что точно такое же, как и в предыдущем методе.
Расчет мощности центробежного компрессора с помощью симулятора процесса Используя симулятор процесса, мы получаем требуемую мощность 0,589 л.с. , что немного ниже расчетного. Но в целом способ правильный.
Но в целом способ правильный.
Я думаю, что трачу слишком много времени на расчет требуемой мощности, используя как адиабатический, так и политропный подходы. Таким образом, лучше использовать адиабатический подход только в том случае, если вы достаточно уверены в расчете.
Возможно, вам потребуется исправить адиабатический КПД. В этом примере я угадал адиабатический КПД. Будет точнее, если вы рассчитаете удельную скорость, чтобы получить точное значение адиабатического КПД на основе графика.
Бонусная таблицаВы можете узнать, как рассчитать мощность центробежного компрессора, используя таблицу, прикрепленную ниже. Я использую пример выше в этой электронной таблице.
Расчет мощности центробежного компрессора
Каталожные номера:
- Практические правила инженеров-химиков – Карл Браннан
- Справочник инженера-химика Perry
: строгий с использованием уравнения состояния и сокращенного метода
В этом совете месяца (TOTM) мы представим расчеты компрессора для тематического исследования.
Расчет мощности
Теоретическая потребность в мощности не зависит от типа компрессора; фактические требования к мощности зависят от эффективности компрессора. Обычно мощность рассчитывается по формуле:
, где массовый расход и ч — удельная энтальпия.
Только с точки зрения расчетов расчет мощности особенно чувствителен к характеристикам расхода, температуры и давления на входе и давления на выходе. Состав газа важен, но небольшая ошибка здесь менее важна, если она не связана с ошибочным исключением коррозионно-активных компонентов. Компрессор будет работать при различных значениях переменных, влияющих на его производительность. Таким образом, наиболее сложной частью расчета компрессора является указание разумного диапазона для каждой переменной, а не сам расчет. В ссылке [1] подчеркивается, что использование одного значения для каждой переменной не является правильным способом оценки системы сжатия.
Компрессор будет работать при различных значениях переменных, влияющих на его производительность. Таким образом, наиболее сложной частью расчета компрессора является указание разумного диапазона для каждой переменной, а не сам расчет. В ссылке [1] подчеркивается, что использование одного значения для каждой переменной не является правильным способом оценки системы сжатия.
Обычно термодинамические расчеты выполняются для идеального (обратимого процесса). Затем результаты обратимого процесса адаптируются к реальному миру с помощью эффективности. В процессе сжатия можно представить себе три идеальных процесса: 1) изотермический процесс, 2) изоэнтропический процесс и 3) политропный процесс. Любой из этих процессов можно надлежащим образом использовать в качестве основы для оценки требований к мощности сжатия либо вручную, либо с помощью компьютера. Однако изотермический процесс редко используется в качестве основы, поскольку обычный промышленный процесс сжатия даже приблизительно не осуществляется при постоянной температуре.
Для изоэнтропического (обратимого и адиабатического) процесса уравнение 1 можно записать как:
и на основе политропного процесса:
Изэнтропический напор рассчитывается по уравнению 3А:
, 900 политропический напор рассчитывается по уравнению 3B:Фактическая температура нагнетания на основе изоэнтропического пути рассчитывается по уравнению 4A.
Фактическая температура нагнетания на основе политропики рассчитывается по уравнению 4B.
where η and η P are the isentropic (or adiabatic) and polytropic efficiency, respectively, P 1 suction pressure, P 2 discharge pressure, T 1 и T 2 – температура всасывания и нагнетания соответственно, q – объемный расход газа при стандартных условиях P S и T S , Z a средний коэффициент сжимаемости газа, k коэффициент теплоемкости, R газовая постоянная, n показатель политропического пути.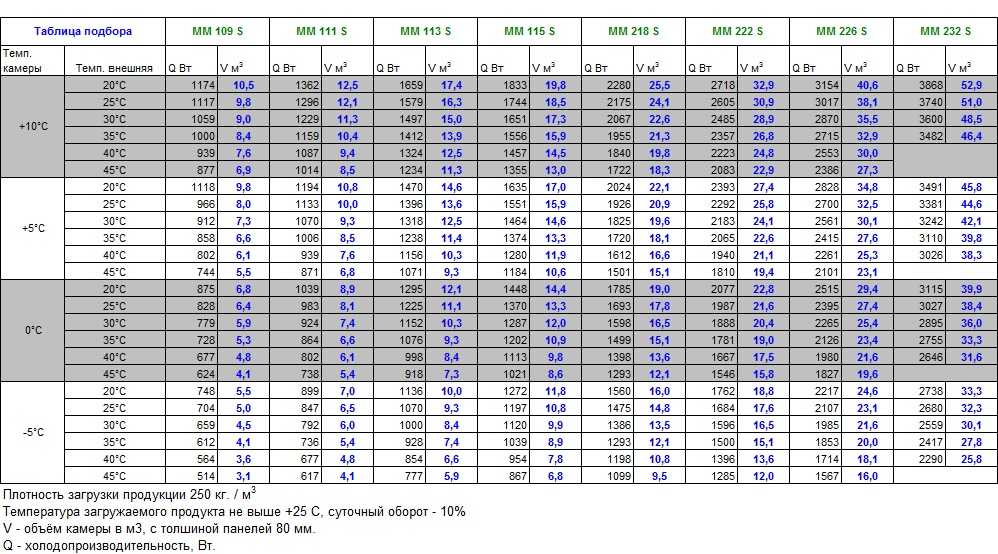 Уравнения 1 и 2 теоретически одинаково верны. Практический выбор зависит от имеющихся данных, хотя и несколько произволен. Расчет мощности должен производиться для каждой ступени сжатия, а затем суммироваться для всех ступеней, подключенных к одному драйверу. Для общих целей планирования графические решения, показанные в ссылке [2], дают результаты, сравнимые с этими уравнениями.
Уравнения 1 и 2 теоретически одинаково верны. Практический выбор зависит от имеющихся данных, хотя и несколько произволен. Расчет мощности должен производиться для каждой ступени сжатия, а затем суммироваться для всех ступеней, подключенных к одному драйверу. Для общих целей планирования графические решения, показанные в ссылке [2], дают результаты, сравнимые с этими уравнениями.
Уравнение состояния (EOS)
Основой любого коммерческого программного обеспечения для моделирования технологических процессов является уравнение состояния. Из-за их простоты и относительной точности обычно используется кубическое уравнение состояния, такое как Соаве Редлих-Квонг (SRK) [3] или Пенг-Робинсон [4]. Эти уравнения используются для расчета фазового поведения, энтальпии и энтропии. При соответствующих коэффициентах бинарного взаимодействия результаты моделирования процесса этих двух уравнений практически совпадают. Поэтому в данной работе использовался только SRK.
Пошаговое компьютерное решение
Для известного расхода газа, давления ( P 1 ), температуры ( T 1 ) и состава на входе и давления нагнетания ( P 2 ), расчет требуемой мощности компрессора основан на EOS с использованием компьютера и включает два этапа:
- Определение идеального или изоэнтропического (обратимого и адиабатического) изменения энтальпии процесса сжатия.
 Требуемая идеальная работа получается путем умножения массовой скорости на изменение изоэнтропической энтальпии.
Требуемая идеальная работа получается путем умножения массовой скорости на изменение изоэнтропической энтальпии. - Регулировка идеального рабочего требования для эффективности компрессора.
Пошаговый расчет на основе EOS описан ниже.- Предположим, стабильное состояние, т. е. состав корма остается неизменным.
- Предположим, что процесс изоэнтропический, т. е. адиабатический и обратимый
- Рассчитать энтальпию ч 1 =f(P 1 , T 1 и состав) и энтропию всасывания с 1 =f(P 1 , T ,0198 и состав) в условиях всасывания по EOS
- Для изоэнтропического процесса . Обратите внимание, что * представляет идеальное значение.
- Рассчитайте идеальную энтальпию () на выходе для известного состава , P 2 и .
- Идеальная работа
- Фактическая работа – это идеальная работа, деленная на эффективность или .
- Фактическая энтальпия на выходе рассчитывается как
- Фактическая температура на выходе рассчитывается EOS для известных h 2 , P 2 и состав.

Эффективность компрессора и, следовательно, процесса сжатия, очевидно, зависит от метода, используемого для оценки потребности в работе. Изэнтропический КПД находится в диапазоне от 0,70 до 0,90.
Если кривая напора компрессора и кривая эффективности предоставлены производителем, напор определяется по фактическому объемному расходу газа на входе. Во-вторых, по напору рассчитываются фактическая работа, давление нагнетания и, наконец, температура нагнетания.
Практический пример
Газовая смесь с составом, показанным в таблице 1, при 105 °F (40,6 °C) и 115 фунтов на кв. дюйм абс. (793 кПа) сжимается с помощью одноступенчатого центробежного компрессора с политропическим напором и кривыми КПД на рисунках 1 и 2 при скорости 7992 об/мин. Общий объемный расход исходного газа составлял 101 млн. стандартных кубических футов в сутки (2,86×10 6 См 3 /сутки).
Общий объемный расход исходного газа составлял 101 млн. стандартных кубических футов в сутки (2,86×10 6 См 3 /сутки).
Таблица 1. Анализ сырьевого газа
Рисунок 1. Политропический напор компрессора и точка максимальной эффективности
Рисунок 2. Политропический КПД компрессора
Результаты и обсуждение данные кривых эффективности были введены в программу ProMax [5] для выполнения строгих расчетов на основе SRK EOS. Программа рассчитывала политропный и изоэнтропический КПД, напор, степень сжатия (давление нагнетания), температуру нагнетания и мощность. Для фактического расхода газа на входе политропный КПД близок к компрессору лучшая точка эффективности (BEP). Программа также рассчитала относительную плотность газа, коэффициент теплоемкости ( k ) и показатель политропы ( n ). Эти расчетные результаты представлены в столбцах SRK Таблицы 2 (цифры жирным шрифтом на белом фоне).
Таблица 2. Сводка результатов точного и ускоренного расчета
Цифры, выделенные жирным шрифтом на белом фоне, являются расчетными значениями
Short-1 (сокращенный метод): В этом методе мы использовали уравнения 2–4 для расчета политропного и изоэнтропического напоров, температуры нагнетания и мощности. Мы использовали рассчитанные ProMax политропный и изоэнтропический КПД, степень сжатия ( P 2 /P 1 ), коэффициент теплоемкости ( k ) и показатель политропы ( n ) для расчета напора, мощности и температура нагнетания. Результаты представлены в short-1 столбцы таблицы 2. Обратите внимание, что результаты short-1 (температура нагнетания, адиабатический и политропный напор и мощность) очень близки к значениям SRK. Фактическая температура нагнетания, рассчитанная по уравнению 4A (изоэнтропический путь: 265,3°F=129,6°C), оказалась немного ниже, чем по уравнению 4B (политропический путь: 265,9°F=129,9°C).
Short-2 (сокращенный метод): Подобно методу short-1 , мы использовали уравнения 2–4 для расчета политропного и изоэнтропического напоров, фактической температуры нагнетания и мощности. Мы использовали только рассчитанные ProMax значения политропной эффективности ( n P ), коэффициент сжатия ( P 2 /P 1 ) и относительная плотность ( y ). Коэффициент теплоемкости ( k ) оценивался по уравнению 5:
Показатель политропы ( n ) оценивался по уравнению 6.
Изэнтропический (адиабатический) КПД () оценивался по уравнению 7
Результаты для этого метода представлены в столбцах short-2 Таблицы 2. Расчетная температура нагнетания по уравнению 4A (изоэнтропический путь) была точно такой же, как по уравнению 4B (политропный). Обратите внимание на short-2 результаты (температура нагнетания, адиабатический и политропный напор и мощность) отклоняются от значений SRK.
Результаты в таблице 2 показывают, что увеличение на 2,2% в k (с 1,224 до 1,251) приводит к увеличению мощности на 1,42%. Показатель политропы ( n ) увеличился на 3%, а изоэнтропическая эффективность () уменьшилась на 0,5%. Разница в фактических значениях температуры нагнетания SRK и Short-2 составляет 17,5 ˚F (9,7 ˚C).
За исключением фактической температуры нагнетания, эти различия между результатами методов SRK и Short-2 для расчетов объектов и целей планирования незначительны. Обратите внимание, что точность сокращенного метода зависит от значений к и н . В методе Short-1 , в котором мы использовали значения k и n из метода SRK, результаты были идентичны результатам метода SRK.
Чтобы узнать больше о подобных случаях и о том, как минимизировать эксплуатационные проблемы, предлагаем посетить курсы Джона М. Кэмпбелла; G4 (кондиционирование и переработка газа) и G5 (кондиционирование и переработка газа – специальные).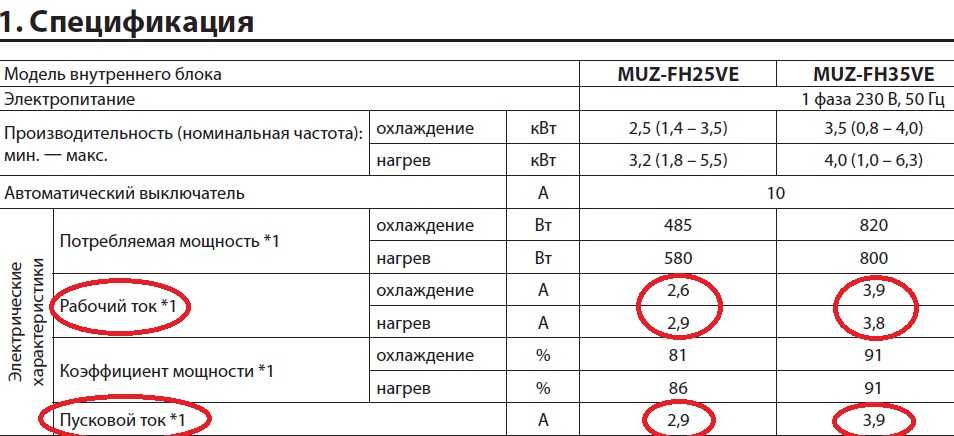

 В случае работы холодильной машины по
циклу теплового насоса (нагрев воздуха),
эффективность работы оценивается
тепловым коэффициентом, учитывающим
потери в прямом и обратном цикле
холодильной машины. Этот коэффициент
можно посчитать по формуле
В случае работы холодильной машины по
циклу теплового насоса (нагрев воздуха),
эффективность работы оценивается
тепловым коэффициентом, учитывающим
потери в прямом и обратном цикле
холодильной машины. Этот коэффициент
можно посчитать по формуле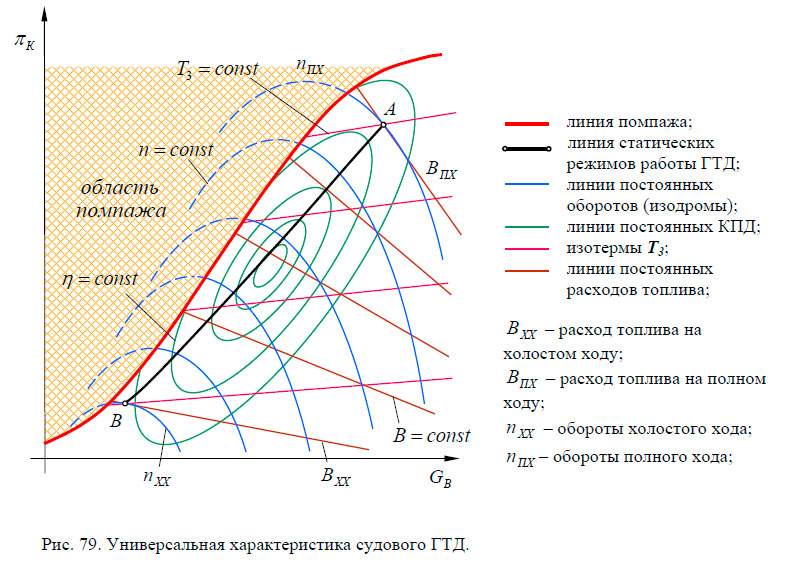 Требуемая идеальная работа получается путем умножения массовой скорости на изменение изоэнтропической энтальпии.
Требуемая идеальная работа получается путем умножения массовой скорости на изменение изоэнтропической энтальпии. 