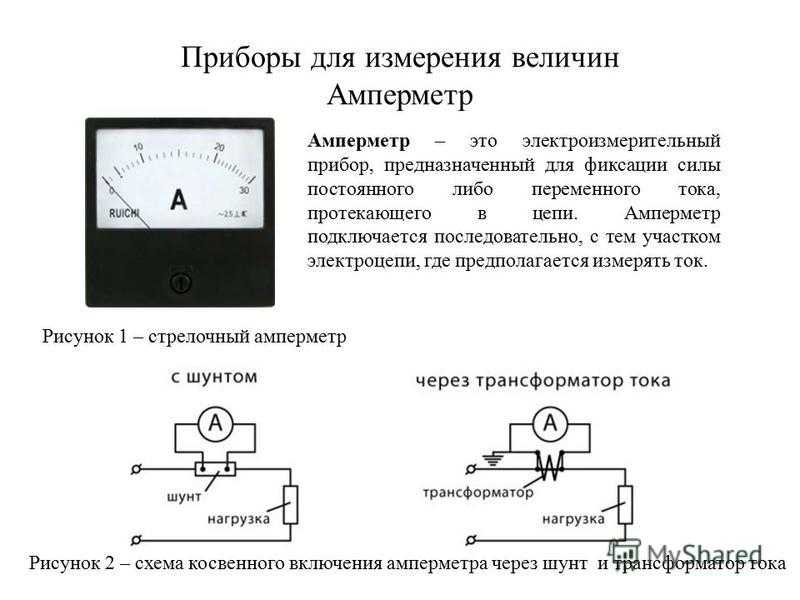
Схема цифрового вольтметра
Здесь предлагается схема цифрового вольтметра, модернизировав которую можно собрать и амперметр.
Вольтметр имеет возможность измерять напряжение от 0 до 99,9 вольт. При этом его диапазон разделен на две части – от 0 до 9,999 вольт и от 10 до 99,99 вольт. Выбор диапазона происходит в автоматическом режиме, что очень удобно и приводит к более точным измерениям. Сопротивление по входу при измерениях в первой части диапазона составляет 470 килоом, а во второй части примерно 100 килоом. Погрешность измерений составляет 3 милливольта. Питается схема напряжением от 15 до 20 вольт (при желании это можно изменить) и потребляет ток в районе 60 миллиампер. Время между измерениями составляет 100 миллисекунд, а время цикла измерений при наличии на входе 10 вольт будет 100 миллисекунд. В случае, если измеряемое напряжение будет выше 99,99 вольт, то на индикаторе отобразится число «9999» и будет мигать 2 раза в секунду.
Работа вольтметра основана на принципе преобразования напряжения, которое измеряется в частоту, однократно интегрируя. Такой метод, в сравнении с контроллерами которые имеют в своем составе АЦП с десятиразрядным преобразованием, позволяет достичь более увеличенной разрешающей способности в более широком диапазоне измеряемых напряжений.
Расчет частоты преобразования, выбор пределов измерения и отображение результатов измерений на семисегментном индикаторе выполняет микроконтроллер.
Исходный код программы, файл с прошивкой, печатную плату, нарисованную в программе Sprint Layout и плату для сборки в SMD варианте можно скачать по ссылке.
Для того чтобы точно подобрать сопротивление резистора R2 в делителе напряжения на входе цифрового вольтметра желательно его заменить на последовательно соединенные резисторы 100 килоом и многооборотный 22 килоома. И R5 так же заменить на подстроечный 15 кОм.
Сам контроллер прошивается программой CodeVisionAVR с помощью программатора STK 200/300. Но можно использовать и другие программы и программаторы.
Ниже показаны Fuse для CodeVisionAVR и Pony Prog.
Питается схема цифрового вольтметра от обычного блока питания на основе трансформатора и микросхемы стабилизатора 7815 по схеме из datasheet. Кроме того на плате блока питания расположены и резисторы R2,R5. Рисунок печатной платы данного блока находится также в архиве, ссылка на который указана выше.
В настройке схемы то же нет ничего сложного. Необходимо с помощью резистора R3 установить ток зарядки С2 и подобрать сопротивление делителя напряжения на входе. Настроив подстроечные резисторы на 117 килоом и 13 килоом соответственно.
Далее, подав на вход напряжение, в пределах от 9 до 9,8 вольт и сверяя показания с эталонным вольтметром, с помощью подстроечного резистора R3, выставляется одинаковое отображение измерений.
На следующем этапе настройки медленно увеличивается напряжение до момента переключения вольтметра на второй диапазон. Если на индикаторе показания зависли, то с помощью резисторов R2 и R5 добиваются состояния переключения и далее повторяется настройка резистора R3.
После этого необходимо подать на вход максимально измеряемое напряжение, это около 100 вольт и с помощью резисторов R2 и R5 производится корректировка показаний.
И последнее. На вход подается напряжение 5-10 вольт и в случае рассогласования производится корректировка с помощью R3.
Отличительной особенностью цифрового вольтметра на основе данного принципа измерения является его высокая точность.
Анекдот:
– Папа, меня в школе все дразнят, говорят, что я страшный.
– Да сейчас ты ничего так выглядишь, сынок. А вот когда ты родился, доктор сказал:”Шевельнется-стреляйте!”./c9f8417bdc1aafe.s.siteapi.org/img/1a99aa89edb7051954ecf3e90a152e0c8ffa5bf0.jpg)
Стрелочный вольтметр с растянутой шкалой 10…15 В
Прибор будет полезен автолюбителям для измерения с высокой точностью напряжения на аккумуляторе, но он может найти и другие применения, где требуется контролировать напряжение в интервале 10…15 В с точностью 0,01 В.
Рис. 1 Вольтметр с растянутой шкалой
Известно, что о степени заряженности автомобильного аккумулятора можно судить по его напряжению. Так, у полностью разряженного, разряженного наполовину и полностью заряженного аккумулятора оно соответствует 11,7, 12,18 и 12,66В.
Для того чтобы измерить напряжение с такой точностью, нужен либо цифровой вольтметр, или стрелочный с растянутой шкалой, позволяющий контролировать интересующий нас интервал.
Схема, приведенная на рис. 1, позволяет, используя любой микроамперметр со шкалой 50 мкА или 100 мкА, сделать из него вольтметр со шкалой измерения 10…15 В.
Схема вольтметра не боится неправильного подключения полярности к измеряемой цепи (в этом случае показания прибора не будут соответствовать измеряемой величине).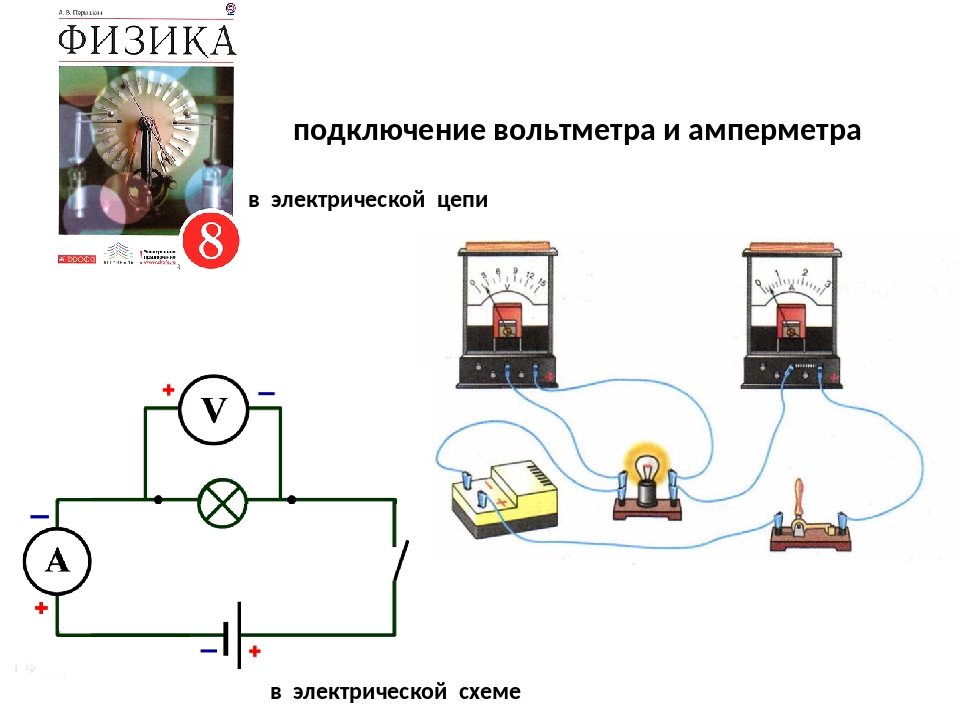
Для предохранения микроамперметра РА1 от повреждения при перевозках используется включатель S1, который при закорачивании выводов измерительного прибора препятствует колебаниям стрелки.
В схеме использован прибор РА1 с зеркальной шкалой, типа М1690А (50 мкА), но подойдут и, многие другие. Прецизионный стабилитрон VD1 (Д818Д) может быть с любой последней буквой в обозначении. Подстроечные резисторы лучше использовать многооборотные, например R2 типа СПЗ-36, R5 типа СП5-2В.
Для настройки схемы потребуется блок питания с регулируемым выходным напряжением О…15 В и образцовый вольтметр (удобней, если он будет цифровым). Настройка заключается в том, чтобы, подключив блок питания к зажимам Х1, Х2 и постепенно увеличивая напряжение до 10 В, добиться резистором R5 “нулевого” положения стрелки прибора РА1. После этого напряжение источника питания увеличиваем до 15 В и резистором R2 устанавливаем стрелку на предельное значение шкалы измерительного прибора. На этом настройку можно считать законченной.
Рис. 2. Схема для более точного измерения сетевого напряжения
На основе данной схемы прибор можно выполнить многофункциональным. Так, если выводы микроамперметра подключать к схеме через галетный переключатель 6П2Н, можно сделать режим обычного вольтметра, подобрав добавочный резистор, а также тестер для проверки цепей и предохранителей.
Прибор можно дополнить схемой (рис. 2) для измерения перемен- ного сетевого напряжения. При этом шкала у него будет от 200 до 300 В, что позволяет более точно измерять сетевое напряжение.
Список радиоэлементов
| Обозначение | Тип | Номинал | Количество | Примечание | Магазин | Мой блокнот | |
|---|---|---|---|---|---|---|---|
| Вольтметр с растянутой шкалой | |||||||
| VD1 | Стабилитрон | Д814Д | 1 | Поиск в магазине Отрон | В блокнот | ||
| R1, R3, R4 | Резистор | 270 Ом | 3 | 1 Ватт | Поиск в магазине Отрон | В блокнот | |
| R2 | Подстроечный резистор | 100 кОм | 1 | Поиск в магазине Отрон | В блокнот | ||
| R5 | Подстроечный резистор | 2. 2 кОм 2 кОм | 1 | Поиск в магазине Отрон | В блокнот | ||
| PA1 | Микроамперметр | М1690А | 1 | Поиск в магазине Отрон | В блокнот | ||
| S1 | Включатель | 1 | Поиск в магазине Отрон | В блокнот | |||
| Схема для более точного измерения сетевого напряжения | |||||||
| VD1-VD4 | Диод | КД243Ж | 4 | Поиск в магазине Отрон | В блокнот | ||
| R1 | Резистор | 12 кОм | 1 | 2 Ватт | Поиск в магазине Отрон | В блокнот | |
| R2, R3 | Резистор | 3. | 2 | 1 Ватт | В блокнот | ||
| C1 | Конденсатор | 0.1 мкФ 400В | 1 | Поиск в магазине Отрон | В блокнот | ||
| Добавить все | |||||||
Скачать список элементов (PDF)
Теги:
- Вольтметр
21.4 Вольтметры и амперметры постоянного тока – College Physics
Резюме
- Объясните, почему вольтметр должен быть подключен параллельно цепи.
- Нарисуйте схему, показывающую правильное подключение амперметра к цепи.
- Опишите, как можно использовать гальванометр как вольтметр или амперметр.
- Найдите сопротивление, которое нужно включить последовательно с гальванометром, чтобы его можно было использовать как вольтметр с заданными показаниями.

- Объясните, почему измерение напряжения или тока в цепи никогда не может быть точным.
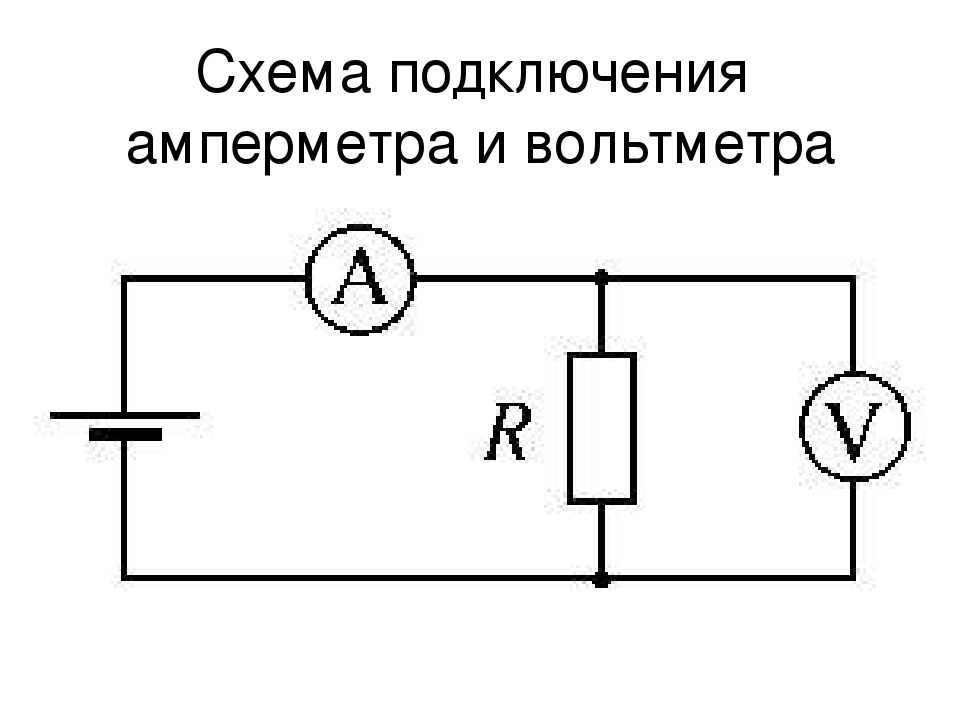
Вольтметры измеряют напряжение, тогда как амперметры измеряют ток. Некоторые счетчики в автомобильных приборных панелях, цифровых камерах, сотовых телефонах и тюнерах-усилителях являются вольтметрами или амперметрами. (См. рис. 1.) Внутренняя конструкция простейших из этих счетчиков и то, как они подключены к системе, которую они контролируют, дают дополнительное представление о применении последовательных и параллельных соединений.
Рисунок 1. Датчики уровня топлива и температуры (крайний правый и крайний левый, соответственно) в этом Volkswagen 1996 года — это вольтметры, которые регистрируют выходное напряжение «передатчиков», которое, как мы надеемся, пропорционально количеству бензина в баке и температура двигателя. (кредит: Кристиан Гирсинг) вольтметров подключены параллельно любому устройству, напряжение которого нужно измерить.
подключаются последовательно к устройству, ток которого нужно измерить. Последовательное соединение используется потому, что последовательно соединенные объекты имеют одинаковый ток, проходящий через них. (См. рис. 3, где амперметр обозначен символом А.)
Рисунок 2. (a) Для измерения разности потенциалов в этой последовательной цепи вольтметр (V) помещают параллельно источнику напряжения или одному из резисторов. Обратите внимание, что напряжение на клеммах измеряется между точками a и b. Невозможно подключить вольтметр непосредственно через ЭДС без учета его внутреннего сопротивления, р . (b) Используемый цифровой вольтметр. (кредит: Messtechniker, Wikimedia Commons) Рис. 3. Амперметр (A) подключен последовательно для измерения тока.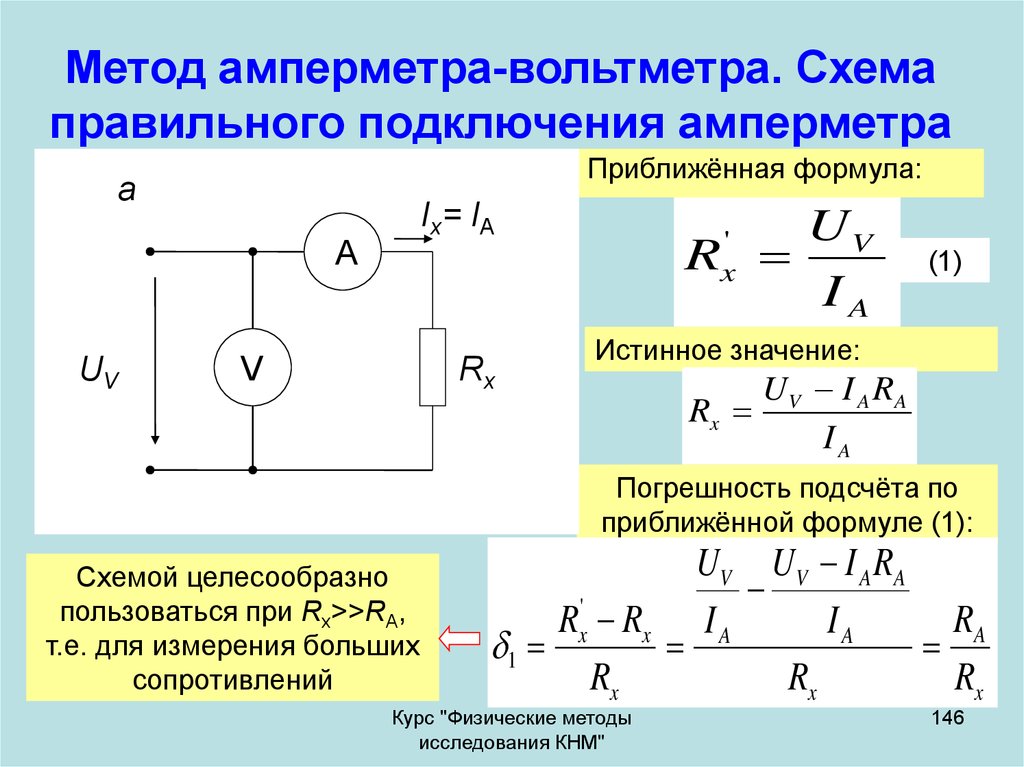 Весь ток в этой цепи протекает через счетчик. Амперметр будет иметь такое же показание, если он будет расположен между точками d и e или между точками f и a, как показано на рисунке. (Обратите внимание, что заглавная буква E обозначает ЭДС, а r обозначает внутреннее сопротивление источника разности потенциалов.)
Весь ток в этой цепи протекает через счетчик. Амперметр будет иметь такое же показание, если он будет расположен между точками d и e или между точками f и a, как показано на рисунке. (Обратите внимание, что заглавная буква E обозначает ЭДС, а r обозначает внутреннее сопротивление источника разности потенциалов.)Аналоговые счетчики имеют стрелку, которая поворачивается, чтобы указывать на числа на шкале, в отличие от цифровых счетчиков , которые имеют числовые показания, подобные ручному калькулятору. Сердцем большинства аналоговых счетчиков является устройство, называемое гальванометром , обозначаемым буквой G. Ток, протекающий через гальванометр $latex \boldsymbol{I_{\textbf{G}}}$, вызывает пропорциональное отклонение стрелки. (Это отклонение происходит из-за силы магнитного поля, действующей на проводник с током.)
Двумя важнейшими характеристиками данного гальванометра являются его сопротивление и чувствительность к току. Чувствительность по току — это ток, который дает полное отклонение стрелки гальванометра, максимальный ток, который может измерить прибор. Например, гальванометр с токовой чувствительностью $latex \boldsymbol{50 \;\mu \textbf{A}} $ имеет максимальное отклонение стрелки, когда $latex \boldsymbol{50 \;\mu \textbf{A} } $ проходит через него, читается наполовину, когда $latex \boldsymbol{25 \;\mu \textbf{A}} $ проходит через него, и так далее.
Чувствительность по току — это ток, который дает полное отклонение стрелки гальванометра, максимальный ток, который может измерить прибор. Например, гальванометр с токовой чувствительностью $latex \boldsymbol{50 \;\mu \textbf{A}} $ имеет максимальное отклонение стрелки, когда $latex \boldsymbol{50 \;\mu \textbf{A} } $ проходит через него, читается наполовину, когда $latex \boldsymbol{25 \;\mu \textbf{A}} $ проходит через него, и так далее.
Если такой гальванометр имеет сопротивление $латекс \boldsymbol{25 – \;\Omega}$, то напряжение всего $латекс \boldsymbol{V = IR = (50 \;\mu \textbf{A}) (25 \;\Omega) = 1,25 \;\textbf{мВ}} $ дает полномасштабное показание. Подключая резисторы к этому гальванометру различными способами, вы можете использовать его как вольтметр или амперметр, который может измерять широкий диапазон напряжений или токов.
Гальванометр как вольтметр
На рис. 4 показано, как можно использовать гальванометр в качестве вольтметра, подключив его последовательно с большим сопротивлением $latex \boldsymbol{R} $. Значение сопротивления $latex \boldsymbol{R} $ определяется максимальным измеряемым напряжением. Предположим, вы хотите, чтобы напряжение 10 В вызывало полное отклонение вольтметра, содержащего $латексный \boldsymbol{25 – \;\Omega} $ гальванометр с $латексным \boldsymbol{50 – \;\mu \textbf{A}} $ чувствительность. Тогда 10 В, подаваемые на счетчик, должны давать ток $latex \boldsymbol{50 \;\mu \textbf{A}} $. Общее сопротивление должно быть
Значение сопротивления $latex \boldsymbol{R} $ определяется максимальным измеряемым напряжением. Предположим, вы хотите, чтобы напряжение 10 В вызывало полное отклонение вольтметра, содержащего $латексный \boldsymbol{25 – \;\Omega} $ гальванометр с $латексным \boldsymbol{50 – \;\mu \textbf{A}} $ чувствительность. Тогда 10 В, подаваемые на счетчик, должны давать ток $latex \boldsymbol{50 \;\mu \textbf{A}} $. Общее сопротивление должно быть
$latex \boldsymbol{R_{\textbf{tot}} = R + r =} $ $latex \boldsymbol{=} $ $latex \boldsymbol{=200 \;\textbf{k} \Omega \;\textbf{ , или}} $
$латекс \boldsymbol{R = R_{\textbf{tot}} – r = 200 \;\textbf{k} \Omega – 25 \;\Omega \примерно 200 \;\textbf{k} \Omega} $
($latex \boldsymbol{R} $ настолько велик, что сопротивлением гальванометра, $latex \boldsymbol{r} $, можно пренебречь). латекс \boldsymbol{25 – \;\mu \textbf{A}} $ ток через счетчик, поэтому показания вольтметра, как и требуется, пропорциональны напряжению.
Этот вольтметр бесполезен при напряжении менее половины вольта, потому что отклонение измерителя будет небольшим и его трудно будет точно считывать. Для других диапазонов напряжения последовательно с гальванометром включают другие сопротивления. Многие счетчики имеют выбор шкалы. Этот выбор включает последовательное включение соответствующего сопротивления с гальванометром.
Рисунок 4. Большое сопротивление R , включенное последовательно с гальванометром Г, дает вольтметр, отклонение которого на полную шкалу зависит от выбора Р . Чем больше измеряемое напряжение, тем больше должно быть R . (Обратите внимание, что r представляет собой внутреннее сопротивление гальванометра.)Гальванометр как амперметр
Тот же гальванометр можно также превратить в амперметр, поместив его параллельно с небольшим сопротивлением $латекс \boldsymbol{R} $, часто называемым шунтовым сопротивлением , как показано на рисунке 5.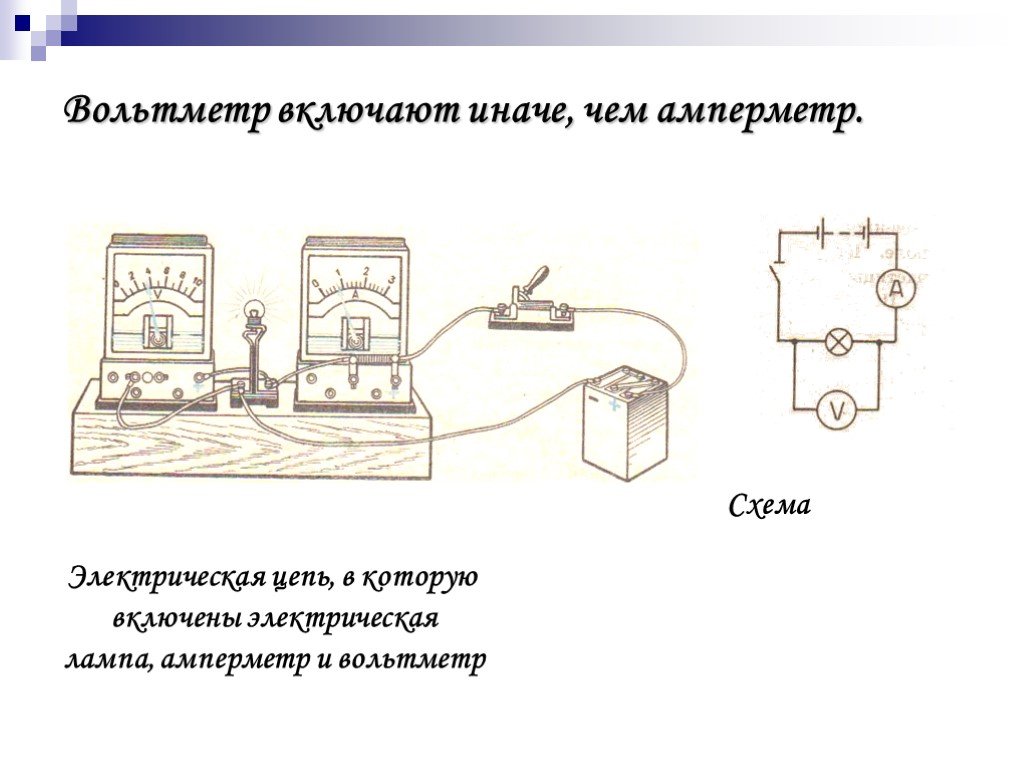 Поскольку шунтирующее сопротивление мало, через него проходит большая часть тока, что позволяет амперметру измерять токи, намного большие, чем те, которые вызывают полное отклонение гальванометра.
Поскольку шунтирующее сопротивление мало, через него проходит большая часть тока, что позволяет амперметру измерять токи, намного большие, чем те, которые вызывают полное отклонение гальванометра.
Допустим, например, нужен амперметр, дающий полное отклонение на 1,0 А, и содержащий тот же $латексный \boldsymbol{25 – \;\Omega} $ гальванометр с его $латексным \boldsymbol{50 – \; \mu \textbf{A}} $ чувствительность. Поскольку $latex \boldsymbol{R} $ и $latex \boldsymbol{r} $ соединены параллельно, напряжение на них одинаково.
Эти капли $latex \boldsymbol{IR} $ являются $latex \boldsymbol{IR = I_Gr} $, так что $latex \boldsymbol{IR = \frac{I_G}{I} = \frac{R}{r}} $ . Находя $latex \boldsymbol{R} $ и учитывая, что $latex \boldsymbol{I_G} $ есть $latex \boldsymbol{50 \;\mu \textbf{A}} $, а $latex \boldsymbol{I} $ есть 0,9{-3} \;\Омега}. $
Рис. 5. Небольшое шунтирующее сопротивление R , помещенное параллельно с гальванометром G, дает амперметр, отклонение на полную шкалу которого зависит от выбора R . Чем больше измеряемый ток, тем меньше должны быть R . Большая часть тока ( I ), протекающего через счетчик, шунтируется через R для защиты гальванометра. (Обратите внимание, что r представляет собой внутреннее сопротивление гальванометра.) Амперметры также могут иметь несколько шкал для большей гибкости в применении. Различные масштабы достигаются включением различных шунтирующих сопротивлений параллельно гальванометру — чем больше максимальный измеряемый ток, тем меньше должно быть шунтирующее сопротивление.
Чем больше измеряемый ток, тем меньше должны быть R . Большая часть тока ( I ), протекающего через счетчик, шунтируется через R для защиты гальванометра. (Обратите внимание, что r представляет собой внутреннее сопротивление гальванометра.) Амперметры также могут иметь несколько шкал для большей гибкости в применении. Различные масштабы достигаются включением различных шунтирующих сопротивлений параллельно гальванометру — чем больше максимальный измеряемый ток, тем меньше должно быть шунтирующее сопротивление.Когда вы используете вольтметр или амперметр, вы подключаете другой резистор к существующей цепи и, таким образом, изменяете схему. В идеале вольтметры и амперметры не оказывают заметного влияния на цепь, но полезно изучить обстоятельства, при которых они влияют или не влияют.
Сначала рассмотрим вольтметр, который всегда ставится параллельно измеряемому устройству.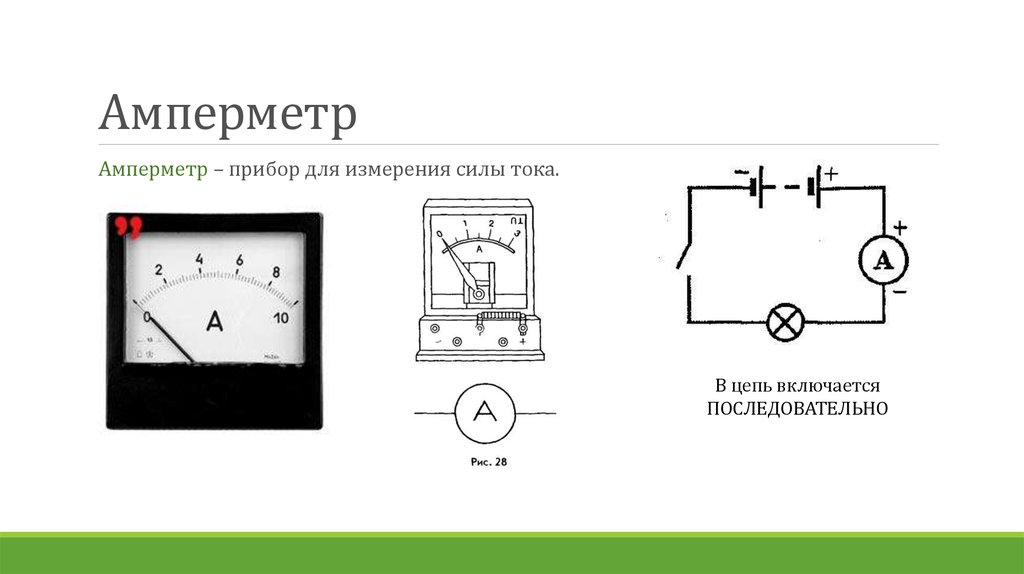 Через вольтметр протекает очень небольшой ток, если его сопротивление на несколько порядков больше, чем сопротивление устройства, и поэтому на цепь не оказывается заметного влияния. (См. рис. 6(а).) (Большое сопротивление, соединенное параллельно с малым, имеет суммарное сопротивление, практически равное малому.) Если, однако, сопротивление вольтметра сравнимо с сопротивлением измеряемого устройства, то два параллельно имеют меньшее сопротивление, заметно влияя на цепь. (См. рис. 6(b).) Напряжение на устройстве не такое, как если бы вольтметр не был включен в цепь.
Через вольтметр протекает очень небольшой ток, если его сопротивление на несколько порядков больше, чем сопротивление устройства, и поэтому на цепь не оказывается заметного влияния. (См. рис. 6(а).) (Большое сопротивление, соединенное параллельно с малым, имеет суммарное сопротивление, практически равное малому.) Если, однако, сопротивление вольтметра сравнимо с сопротивлением измеряемого устройства, то два параллельно имеют меньшее сопротивление, заметно влияя на цепь. (См. рис. 6(b).) Напряжение на устройстве не такое, как если бы вольтметр не был включен в цепь.
 Это пример существенного изменения схемы, которого следует избегать.
Это пример существенного изменения схемы, которого следует избегать.Амперметр включен последовательно в измеряемую ветвь цепи, так что его сопротивление добавляется к этой ветви. Обычно сопротивление амперметра очень мало по сравнению с сопротивлениями устройств в цепи, поэтому лишнее сопротивление незначительно. (См. рис. 7(а).) Однако, если используются очень малые сопротивления нагрузки или если сопротивление амперметра не такое низкое, как должно быть, то общее последовательное сопротивление будет значительно больше, а ток в ответвлении составит измеряемое уменьшается. (См. рис. 7(b).)
При неправильном подключении амперметра может возникнуть практическая проблема. Если бы он был подключен параллельно резистору для измерения тока в нем, вы могли бы повредить счетчик; низкое сопротивление амперметра позволило бы большей части тока в цепи проходить через гальванометр, и этот ток был бы больше, поскольку эффективное сопротивление меньше.
Рисунок 7. (a) Обычно амперметр имеет настолько малое сопротивление, что общее последовательное сопротивление в измеряемой ветви не увеличивается заметно.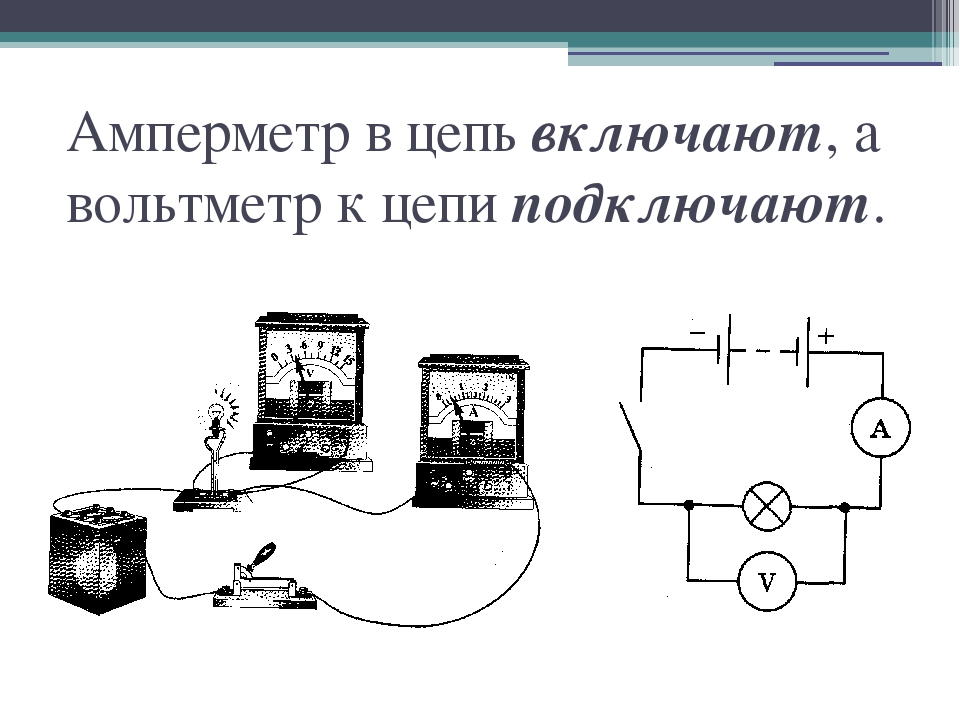 Схема практически не изменилась по сравнению с отсутствием амперметра. (b) Здесь сопротивление амперметра такое же, как сопротивление ответвления, так что общее сопротивление удваивается, а ток вдвое меньше, чем без амперметра. Этого значительного изменения схемы следует избегать.
Схема практически не изменилась по сравнению с отсутствием амперметра. (b) Здесь сопротивление амперметра такое же, как сопротивление ответвления, так что общее сопротивление удваивается, а ток вдвое меньше, чем без амперметра. Этого значительного изменения схемы следует избегать.Одним из решений проблемы помех вольтметров и амперметров в измеряемых цепях является использование гальванометров с большей чувствительностью. Это позволяет создавать вольтметры с большим сопротивлением и амперметры с меньшим сопротивлением, чем при использовании менее чувствительных гальванометров.
Существуют практические пределы чувствительности гальванометра, но можно получить аналоговые измерители, точность измерений которых составляет несколько процентов. Обратите внимание, что неточность возникает из-за изменения схемы, а не из-за неисправности счетчика.
Connections: Limits to Knowledge
Выполнение измерения изменяет измеряемую систему таким образом, что возникает неопределенность в измерении. Для макроскопических систем, таких как схемы, обсуждаемые в этом модуле, изменение обычно можно сделать пренебрежимо малым, но полностью устранить его нельзя. Для субмикроскопических систем, таких как атомы, ядра и более мелкие частицы, измерение изменяет систему таким образом, что ее нельзя сделать произвольно малой. Это фактически ограничивает знание системы — даже ограничивает то, что природа может знать о себе. Мы увидим глубокие последствия этого, когда принцип неопределенности Гейзенберга будет обсуждаться в модулях по квантовой механике. 96} $.
Для макроскопических систем, таких как схемы, обсуждаемые в этом модуле, изменение обычно можно сделать пренебрежимо малым, но полностью устранить его нельзя. Для субмикроскопических систем, таких как атомы, ядра и более мелкие частицы, измерение изменяет систему таким образом, что ее нельзя сделать произвольно малой. Это фактически ограничивает знание системы — даже ограничивает то, что природа может знать о себе. Мы увидим глубокие последствия этого, когда принцип неопределенности Гейзенберга будет обсуждаться в модулях по квантовой механике. 96} $.
PhET Explorations: набор для построения схемы (только DC), виртуальная лаборатория
Стимулируйте нейрон и следите за происходящим. Делайте паузы, перематывайте назад и двигайтесь вперед во времени, чтобы наблюдать за движением ионов через мембрану нейрона.
Рис. 8. Комплект для построения схемы (только для постоянного тока), виртуальная лаборатория- Вольтметры измеряют напряжение, а амперметры измеряют ток.

- Вольтметр размещается параллельно источнику напряжения для получения полного напряжения и должен иметь большое сопротивление, чтобы ограничить его влияние на цепь.
- Амперметр включен последовательно, чтобы получить полный ток, протекающий через ветвь, и должен иметь небольшое сопротивление, чтобы ограничить его влияние на цепь.
- Оба могут быть основаны на комбинации резистора и гальванометра, устройства, которое дает аналоговое считывание тока.
- Стандартные вольтметры и амперметры изменяют измеряемую цепь и, таким образом, имеют ограниченную точность.
Задача Упражнения
1: Какова чувствительность гальванометра (т. е. какой ток дает полное отклонение) внутри вольтметра, имеющего $latex \boldsymbol{1.00 – \;\textbf{M} \ Сопротивление Omega} $ по шкале 30,0 В?
2: Какова чувствительность гальванометра (то есть какой ток дает полное отклонение) внутри вольтметра, имеющего $latex \boldsymbol{25. 0 – \;\textbf{k} \Omega} $ сопротивление по шкале 100 В?
0 – \;\textbf{k} \Omega} $ сопротивление по шкале 100 В?
3: Найдите сопротивление, которое необходимо включить последовательно с гальванометром $latex \boldsymbol{25,0 – \;\Omega} $, имеющим $latex \boldsymbol{50,0 – \;\mu \textbf{A}} $ чувствительность (такая же, как обсуждалась в тексте), чтобы можно было использовать его в качестве вольтметра с полным отсчетом 0,100 В.
4: Найдите сопротивление, которое нужно включить последовательно с гальванометром $latex \boldsymbol{25,0 – \;\Omega} $, имеющим $latex \boldsymbol{50,0 – \;\mu \textbf{A}} $ чувствительность (такая же, как рассмотренная в тексте), позволяющая использовать его в качестве вольтметра с полным отсчетом 3000 В. Включите принципиальную схему с вашим решением.
5: Найдите сопротивление, которое необходимо подключить параллельно гальванометру $latex \boldsymbol{25,0 – \;\Omega} $ с чувствительностью $latex \boldsymbol{50,0 – \;\textbf{A}} $ (такой же, как обсуждаемый в тексте), чтобы его можно было использовать в качестве амперметра с полным отсчетом 10,0 А. Включите принципиальную схему с вашим решением.
Включите принципиальную схему с вашим решением.
6: Найдите сопротивление, которое необходимо подключить параллельно гальванометру $latex \boldsymbol{25,0 – \;\Omega} $, имеющему $latex \boldsymbol{50,0 – \;\mu \textbf{A}} $ чувствительность (такая же, как рассмотренная в тексте), чтобы можно было использовать его в качестве амперметра с полным отсчетом 300 мА.
7: Найдите сопротивление, которое нужно включить последовательно с $латексным \boldsymbol{10.0 – \;\Omega} $ гальванометром, имеющим $латексный \boldsymbol{100 – \;\mu \textbf{A}} $ чувствительность, чтобы его можно было использовать в качестве вольтметра с: (а) показанием полной шкалы 300 В и (б) показанием полной шкалы 0,300 В.
8: Найдите сопротивление, которое необходимо подключить параллельно $латексному \boldsymbol{10.0 – \;\Omega} $ гальванометру, имеющему $латексный \boldsymbol{100 – \;\mu \textbf{A}} $ чувствительность, чтобы его можно было использовать в качестве амперметра с: (a) показанием полной шкалы 20,0 А и (b) полномасштабным показанием 100 мА.
9: Предположим, вы измеряете напряжение на клеммах щелочного элемента на 1,585 В, имеющего внутреннее сопротивление $latex \boldsymbol{0,100 \;\Omega} $, поместив $latex \boldsymbol{1,00 – \;\textbf {k} \Omega} $ вольтметр на его клеммах. (См. рис. 11.) а) Какой ток течет? (b) Найдите напряжение на клеммах. в) Чтобы увидеть, насколько близко измеренное напряжение на клеммах к ЭДС, рассчитайте их отношение.
Рисунок 11.10: Предположим, вы измеряете напряжение на клеммах литиевого элемента на 3,200 В, имеющего внутреннее сопротивление $latex \boldsymbol{5,00 \;\Omega} $, поместив $latex \boldsymbol{1,00 – \;\textbf{k} \Omega} $ вольтметр на его клеммах. а) Какой ток течет? (b) Найдите напряжение на клеммах. в) Чтобы увидеть, насколько близко измеренное напряжение на клеммах к ЭДС, рассчитайте их отношение.
11: Определенный амперметр имеет сопротивление $latex \boldsymbol{5,00 \times 10^{-5} \;\Omega} $ по шкале 3,00-A и содержит $latex \boldsymbol{10,0 – \ ;\Omega} $ гальванометр. Какова чувствительность гальванометра?
Какова чувствительность гальванометра?
12: Вольтметр $latex \boldsymbol{1.00 – \;\textbf{M} \Omega} $ подключен параллельно $latex \boldsymbol{75.0 – \;\textbf{k} \Omega} $ резистор в цепи. а) Нарисуйте схему соединения. б) Чему равно сопротивление комбинации? (c) Если напряжение на комбинации остается таким же, как и на одном резисторе $latex \boldsymbol{75,0 – \;\textbf{k} \Omega} $, на сколько процентов увеличится ток? (d) Если ток через комбинацию остается таким же, как и через резистор $latex \boldsymbol{75,0 – \;\textbf{k} \Omega} $, на сколько процентов уменьшается напряжение? (e) Являются ли существенными изменения, обнаруженные в частях (c) и (d)? Обсуждать.
13: Латексный \boldsymbol{0,0200 – \;\Omega} $ амперметр включен в цепь последовательно с $латексным \boldsymbol{10,00 – \;\Omega} $ резистором. а) Нарисуйте схему соединения. (b) Рассчитайте сопротивление комбинации. (c) Если напряжение остается таким же на всей комбинации, как и на одном резисторе $latex \boldsymbol{10.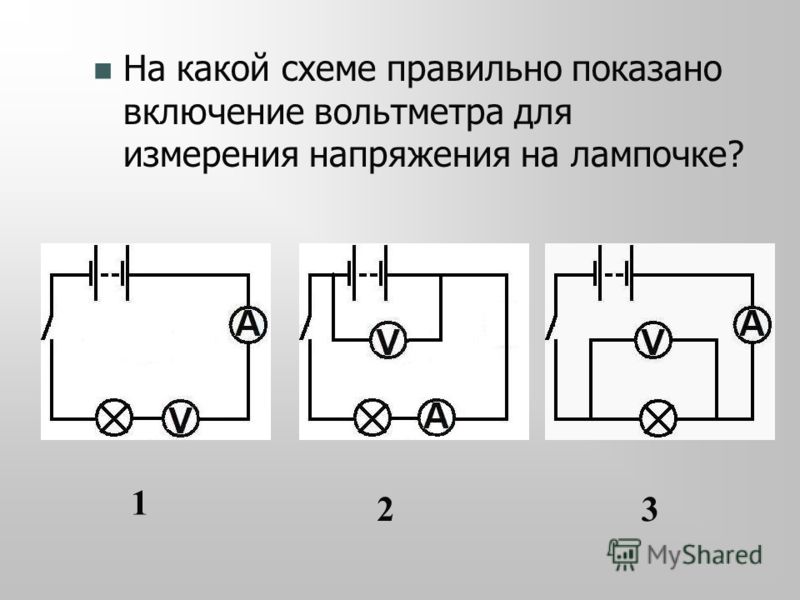 00 – \;\Omega} $, на сколько процентов уменьшится ток? (d) Если ток поддерживается таким же через комбинацию, как и через резистор $latex \boldsymbol{10.00 – \;\Omega} $, на сколько процентов увеличится напряжение? (e) Являются ли существенными изменения, обнаруженные в частях (c) и (d)? Обсуждать.
00 – \;\Omega} $, на сколько процентов уменьшится ток? (d) Если ток поддерживается таким же через комбинацию, как и через резистор $latex \boldsymbol{10.00 – \;\Omega} $, на сколько процентов увеличится напряжение? (e) Являются ли существенными изменения, обнаруженные в частях (c) и (d)? Обсуждать.
14: Необоснованные результаты
Предположим, у вас есть гальванометр $latex \boldsymbol{40,0 – \;\Omega} $ с чувствительностью $latex \boldsymbol{25,0 – \;\mu \textbf{A}} $. а) Какое сопротивление вы бы включили с ним последовательно, чтобы его можно было использовать в качестве вольтметра с полным отклонением 0,500 мВ? б) Что неразумного в этом результате? (c) Какие предположения ответственны?
15: Необоснованные результаты
(a) Какое сопротивление вы бы подключили параллельно $латексному \boldsymbol{40,0 – \;\Omega} $ гальванометру, имеющему
$latex \boldsymbol{25.0 – \;\mu \textbf{A}} $ чувствительность, позволяющая использовать его в качестве амперметра с полным отклонением для $latex \boldsymbol{10. 0 – \;\mu \textbf {А}} $? б) Что неразумного в этом результате? (c) Какие предположения ответственны?
0 – \;\mu \textbf {А}} $? б) Что неразумного в этом результате? (c) Какие предположения ответственны?
Глоссарий
- Вольтметр
- прибор для измерения напряжения
- амперметр
- прибор для измерения силы тока
- аналоговый счетчик
- измерительный прибор, дающий показания в виде движения стрелки по маркированному калибру
- цифровой счетчик
- измерительный прибор, дающий показания в цифровой форме
- гальванометр
- аналоговое измерительное устройство, обозначенное буквой G, которое измеряет ток, используя отклонение стрелки, вызванное силой магнитного поля, действующей на проводник с током
- чувствительность по току
- максимальный ток, который может считывать гальванометр
- полное отклонение
- максимальное отклонение стрелки гальванометра, также известное как токовая чувствительность; гальванометр с полным отклонением $latex \boldsymbol{50 \;\mu \textbf{A}} $ имеет максимальное отклонение своей стрелки, когда $latex \boldsymbol{50 \;\mu \textbf{A}} $ течет через него
- Шунтирующее сопротивление
- маленькое сопротивление $латекс \boldsymbol{R}$, помещенное параллельно гальванометру G для получения амперметра; чем больше измеряемый ток, тем меньше должен быть $latex \boldsymbol{R} $; большая часть тока, протекающего через счетчик, шунтируется через $латекс \boldsymbol{R} $ для защиты гальванометра
20.
 4: Вольтметры и амперметры – Физика LibreTexts
4: Вольтметры и амперметры – Физика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14567
- Boundless (теперь LumenLearning)
- Безграничный
учебные цели
- Сравнить схему подключения амперметра и вольтметра
Вольтметры и амперметры измеряют соответственно напряжение и ток в цепи. Некоторые измерители в автомобильных приборных панелях, цифровых камерах, сотовых телефонах и тюнерах-усилителях являются вольтметрами или амперметрами.
Вольтметры и амперметры : Краткое введение в вольтметры и амперметры для начинающих физиков.
Вольтметры
Вольтметр — это прибор, измеряющий разность электрических потенциалов между двумя точками электрической цепи. Аналоговый вольтметр перемещает стрелку по шкале пропорционально напряжению цепи; цифровой вольтметр обеспечивает числовой дисплей. Любое измерение, которое можно преобразовать в напряжение, можно отобразить на правильно откалиброванном измерителе; такие измерения включают давление, температуру и расход.
Вольтметр : Демонстрационный вольтметр из класса физики
Чтобы вольтметр мог измерять напряжение устройства, он должен быть подключен параллельно этому устройству. Это необходимо, потому что параллельные объекты испытывают одинаковую разность потенциалов.
Параллельный вольтметр : (a) Для измерения разности потенциалов в этой последовательной цепи вольтметр (V) помещается параллельно источнику напряжения или одному из резисторов. Обратите внимание, что напряжение на клеммах измеряется между точками a и b. Невозможно подключить вольтметр непосредственно к ЭДС без учета его внутреннего сопротивления r. (b) Используемый цифровой вольтметр
Невозможно подключить вольтметр непосредственно к ЭДС без учета его внутреннего сопротивления r. (b) Используемый цифровой вольтметр
Амперметры
Амперметр измеряет электрический ток в цепи. Название происходит от названия единицы СИ для электрического тока, ампер (А).
Чтобы амперметр мог измерять ток устройства, он должен быть подключен последовательно к этому устройству. Это необходимо, потому что объекты, соединенные последовательно, испытывают одинаковый ток. Они не должны быть подключены к источнику напряжения — амперметры рассчитаны на работу с минимальной нагрузкой (которая относится к падению напряжения на амперметре, обычно составляющему небольшую долю вольта).
Амперметр в серии : Амперметр (А) включен последовательно для измерения тока. Весь ток в этой цепи протекает через счетчик. Амперметр будет иметь такое же показание, если он будет расположен между точками d и e или между точками f и a, как показано на рисунке.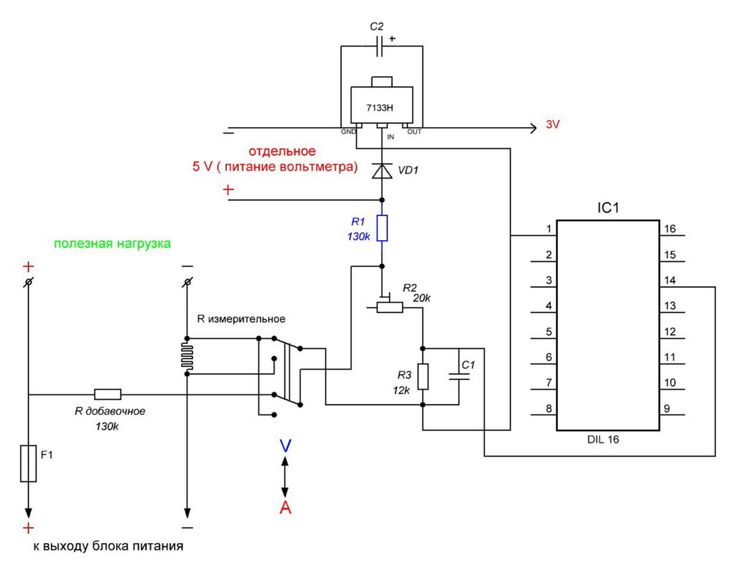 (Обратите внимание, что заглавная буква E обозначает ЭДС, а r обозначает внутреннее сопротивление источника разности потенциалов.)
(Обратите внимание, что заглавная буква E обозначает ЭДС, а r обозначает внутреннее сопротивление источника разности потенциалов.)
Гальванометры (аналоговые измерители)
Аналоговые измерители имеют стрелки, которые поворачиваются, чтобы указывать на числа на шкале, как в отличие от цифровых счетчиков, которые имеют числовые показания. Сердцем большинства аналоговых счетчиков является устройство, называемое гальванометром, обозначаемое цифрой 9.0030 Г . Протекание тока через гальванометр I G вызывает пропорциональное движение или отклонение стрелки.
Двумя важнейшими характеристиками любого гальванометра являются его сопротивление и чувствительность к току. Чувствительность по току — это ток, при котором происходит полное отклонение стрелки гальванометра, иначе говоря, максимальный ток, который может измерить прибор. Например, гальванометр с токовой чувствительностью 50 мкА имеет максимальное отклонение стрелки при протекании через нее 50 мкА, находится на середине шкалы при протекании через нее 25 мкА и т. д.
д.
Если такой гальванометр имеет сопротивление 25 Ом, то напряжение всего \(\mathrm{V = IR = (50 мкА)(25 оммега)=1,25 \; мВ}\) дает полное чтение шкалы. Подключая резисторы к этому гальванометру различными способами, вы можете использовать его как вольтметр или амперметр для измерения широкого диапазона напряжений или токов.
Гальванометры в качестве вольтметров
Гальванометр может работать как вольтметр, когда он соединен последовательно с большим сопротивлением Ом . Значение R определяется максимальным напряжением, которое будет измеряться. Предположим, вы хотите, чтобы 10 В производили полное отклонение вольтметра, содержащего гальванометр на 25 Ом с чувствительностью 50 мкА. Тогда 10 В, подаваемые на счетчик, должны давать ток 50 мкА. Общее сопротивление должно быть:
\[\mathrm { R } _ { \mathrm { tot } } = \ mathrm { R } + \ mathrm { r } = \ dfrac { \ mathrm { V } } { \ mathrm { I } } = \frac { 10 \mathrm { V } } { 50 \mu \mathrm { A } } = 200 \mathrm { k } \Omega\]
или:
\[\mathrm { R } = \ mathrm { R } _ { \ mathrm { tot } } – \ mathrm { r } = 200 \ mathrm { k } \ Omega – 25 \ Omega \ приблизительно 200 \ mathrm { k } \Omega\]
(R настолько велико, что сопротивлением гальванометра r почти можно пренебречь. ) Обратите внимание, что 5 В, приложенное к этому вольтметру, вызывает отклонение на половину шкалы, поскольку через него проходит ток 25 мкА. метр, и поэтому показания вольтметра пропорциональны напряжению, как и требуется. Этот вольтметр был бы бесполезен для напряжений менее половины вольта, потому что отклонение измерителя было бы слишком маленьким для точного считывания. Для других диапазонов напряжения последовательно с гальванометром включают другие сопротивления. Многие измерители позволяют выбирать шкалы, что включает последовательное включение соответствующего сопротивления с гальванометром.
) Обратите внимание, что 5 В, приложенное к этому вольтметру, вызывает отклонение на половину шкалы, поскольку через него проходит ток 25 мкА. метр, и поэтому показания вольтметра пропорциональны напряжению, как и требуется. Этот вольтметр был бы бесполезен для напряжений менее половины вольта, потому что отклонение измерителя было бы слишком маленьким для точного считывания. Для других диапазонов напряжения последовательно с гальванометром включают другие сопротивления. Многие измерители позволяют выбирать шкалы, что включает последовательное включение соответствующего сопротивления с гальванометром.
Гальванометры в качестве амперметров
Тот же гальванометр может также работать как амперметр, если он подключен параллельно с небольшим сопротивлением R , часто называемым шунтирующим сопротивлением. Поскольку сопротивление шунта невелико, большая часть тока проходит через него, что позволяет амперметру измерять токи, намного большие, чем те, которые вызвали бы полное отклонение гальванометра.
Предположим, например, что нам нужен амперметр, дающий полное отклонение на 1,0 А и содержащий такой же гальванометр на 25 Ом с чувствительностью 50 мкА. С R и r включены параллельно, напряжение на них одинаковое.
Эти капли IR: IR = I G r
, так что: } = \ frac { \ mathrm { R } } { \ mathrm { r } } \).
Решая для R и учитывая, что IG равен 50 мкА, а I равен 0,999950 А, мы имеем:
\[\mathrm { R } = \mathrm { r } \frac { \mathrm { I } _ { \mathrm { G } } } { \ mathrm { I } } = ( 25 \ Omega ) \ frac { 50 \ mu \ mathrm { A } } { 0,9{ – 3 } \Omega\]
Нулевые измерения
Нулевые измерения уравновешивают напряжения, поэтому через измерительные устройства не протекает ток, который может мешать измерению.
цели обучения
- Объясните, почему используются нулевые измерения
Нулевые измерения
Стандартные измерения напряжения и тока изменяют цепи, внося числовые погрешности. Вольтметры потребляют дополнительный ток, тогда как амперметры уменьшают ток. Нулевые измерения уравновешивают напряжения, поэтому через измерительное устройство не протекает ток, и цепь остается неизменной. Измерения нуля, как правило, более точные, но более сложные, чем стандартные вольтметры и амперметры. Их точность все еще ограничена.
Вольтметры потребляют дополнительный ток, тогда как амперметры уменьшают ток. Нулевые измерения уравновешивают напряжения, поэтому через измерительное устройство не протекает ток, и цепь остается неизменной. Измерения нуля, как правило, более точные, но более сложные, чем стандартные вольтметры и амперметры. Их точность все еще ограничена.
Потенциометр
При измерении ЭДС батареи и подключении батареи напрямую к стандартному вольтметру, как показано на рисунке, фактическая измеряемая величина представляет собой напряжение на клеммах В. Напряжение связано с ЭДС батареи соотношением V = эдс − Ir , где I — протекающий ток, а r — внутреннее сопротивление батареи.
Вольтметр, подключенный к батарее : Аналоговый вольтметр, подключенный к батарее, потребляет небольшой, но ненулевой ток и измеряет напряжение на клеммах, которое отличается от ЭДС батареи. (Обратите внимание, что заглавная буква E символизирует электродвижущую силу или ЭДС. ) Поскольку внутреннее сопротивление батареи точно неизвестно, точно рассчитать ЭДС невозможно.
) Поскольку внутреннее сопротивление батареи точно неизвестно, точно рассчитать ЭДС невозможно.
ЭДС можно было бы точно рассчитать, если бы были известны r , что бывает редко. Если бы ток I можно было сделать равным нулю, то В = ЭДС , и можно было бы непосредственно измерить ЭДС. Однако для работы стандартных вольтметров требуется ток.
Потенциометр представляет собой нулевой измерительный прибор для измерения потенциалов (напряжений). К резистору R, подключен источник напряжения, пропуская через него постоянный ток. Вдоль провода наблюдается устойчивое падение потенциала (падение ИК), поэтому за счет контакта по проводу получается переменный потенциал.
Неизвестная ЭДС x (обозначается скриптом E x ), соединенная последовательно с гальванометром, показана на рисунке. Обратите внимание, что ЭДС x противодействует другому источнику напряжения. Положение точки контакта регулируется до тех пор, пока гальванометр не покажет ноль. Когда гальванометр показывает ноль, ЭДС х = IR х , где R х — сопротивление участка провода до точки контакта. Поскольку ток через гальванометр не течет, через неизвестную ЭДС ничего не течет, и emf x воспринимается.
Когда гальванометр показывает ноль, ЭДС х = IR х , где R х — сопротивление участка провода до точки контакта. Поскольку ток через гальванометр не течет, через неизвестную ЭДС ничего не течет, и emf x воспринимается.
Потенциометр : Потенциометр является нулевым измерительным устройством. (а) Источник напряжения, подключенный к длинному проволочному резистору, пропускает через него постоянный ток I. (b.) Неизвестная ЭДС (обозначенная буквой Ex) подключена, как показано, и точка контакта вдоль R регулируется до тех пор, пока гальванометр не покажет ноль. Отрезок провода имеет сопротивление Rx и сценарий Ex=IRx, где I не зависит от соединения, так как через гальванометр не протекает ток. Таким образом, неизвестная ЭДС пропорциональна сопротивлению отрезка провода.
Стандартная ЭДС заменяется на ЭДС x , и точка контакта регулируется до тех пор, пока гальванометр не покажет ноль, так что ЭДС s = IR s . В обоих случаях ток через гальванометр не проходит. Ток I по длинному проводу идентичен. Взяв отношение эдс x / эдс s , I , и найдя эдс x , получим то, что видно на
В обоих случаях ток через гальванометр не проходит. Ток I по длинному проводу идентичен. Взяв отношение эдс x / эдс s , I , и найдя эдс x , получим то, что видно на
Поскольку для R используется длинная однородная проволока, отношение сопротивлений R x /R s такое же, как отношение длин проволоки, которая обнуляет гальванометр для каждой ЭДС. Три величины в правой части уравнения теперь известны или измерены, и можно вычислить ЭДС x . Часто в этом расчете меньше неопределенности, чем при непосредственном использовании вольтметра, но она не равна нулю. Всегда есть некоторая неопределенность в соотношении сопротивлений R x /R s и в стандартных ЭДС. Кроме того, невозможно сказать, когда гальванометр показывает точно ноль, что вносит ошибку как в R x , так и в R s , а также может повлиять на ток I .
Измерение сопротивления
Многие так называемые омметры измеряют сопротивление. Наиболее распространенные омметры применяют напряжение к сопротивлению, измеряют ток и вычисляют сопротивление, используя закон Ома. Их показания – это расчетное сопротивление. Простые конфигурации с использованием стандартных вольтметров и амперметров имеют ограниченную точность, поскольку счетчики изменяют как напряжение, подаваемое на резистор, так и ток, протекающий через него. Мост Уитстона представляет собой нулевой измерительный прибор для расчета сопротивления путем уравновешивания падений потенциала в цепи. Устройство называется мостом, потому что гальванометр образует мост между двумя ветвями. Различные мостовые устройства используются для измерения нуля в цепях. Резисторы R 1 и R 2 точно известны, а стрелка через R 3 указывает, что это переменное сопротивление. Значение R 3 можно точно прочитать. При неизвестном сопротивлении Rx в цепи R 3 регулируют до тех пор, пока гальванометр не покажет ноль.
При неизвестном сопротивлении Rx в цепи R 3 регулируют до тех пор, пока гальванометр не покажет ноль.
Мост Уитстона : Мост Уитстона используется для расчета неизвестных сопротивлений. Переменное сопротивление R3 регулируется до тех пор, пока гальванометр не покажет ноль при замкнутом выключателе. Это упрощает схему, позволяя рассчитать Rx на основе IR-падений.
Разность потенциалов между точками b и d тогда равна нулю, а это означает, что b и d имеют одинаковый потенциал. Без тока, протекающего через гальванометр, он не влияет на остальную часть цепи. Таким образом, ветви abc и adc параллельны, и каждая ветвь имеет полное напряжение источника. Поскольку b и d имеют одинаковый потенциал, падение ИК вдоль и должно равняться падению ИК вдоль аб . Опять же, поскольку b и d имеют одинаковый потенциал, падение ИК вдоль dc должно равняться падению ИК вдоль bc . Это уравнение используется для расчета неизвестного сопротивления, когда ток через гальванометр равен нулю. Этот метод может быть очень точным, но он ограничен двумя факторами. Во-первых, ток через гальванометр не может быть точно равен нулю. Во-вторых, всегда есть неопределенности в R 1 , R 2 и R 3 , которые вносят вклад в неопределенность R x .
Это уравнение используется для расчета неизвестного сопротивления, когда ток через гальванометр равен нулю. Этот метод может быть очень точным, но он ограничен двумя факторами. Во-первых, ток через гальванометр не может быть точно равен нулю. Во-вторых, всегда есть неопределенности в R 1 , R 2 и R 3 , которые вносят вклад в неопределенность R x .
Ключевые точки
- Вольтметр — это прибор, используемый для измерения разности электрических потенциалов между двумя точками в электрической цепи.
- Амперметр — это измерительный прибор, используемый для измерения электрического тока в цепи.
- Вольтметр подключен параллельно устройству для измерения его напряжения, а амперметр подключен последовательно к устройству для измерения его тока.
- В основе большинства аналоговых счетчиков лежит гальванометр, прибор, который измеряет ток с помощью движения или отклонения стрелки. Отклонение стрелки производится магнитной силой, действующей на проводник с током.

- Измерения напряжения и тока стандартными вольтметрами и амперметрами изменяют измеряемую цепь, внося погрешности. Вольтметры потребляют дополнительный ток, тогда как амперметры уменьшают ток.
- Нулевые измерения используются для уменьшения погрешности измерения напряжения и тока.
- Потенциометр и мост Уитстона — это два метода измерения нуля.
- Потенциометр — это прибор, который измеряет неизвестное напряжение путем противодействия известному напряжению, не потребляя ток от измеряемого источника напряжения.
- Мост Уитстона представляет собой электрическую цепь, используемую для измерения неизвестного электрического сопротивления путем уравновешивания двух ветвей мостовой схемы, одна из которых включает неизвестный компонент.
Ключевые термины
- шунтирующее сопротивление : небольшое сопротивление R, включенное параллельно гальванометру G для получения амперметра; чем больше измеряемый ток, тем меньше должно быть R; большая часть тока, протекающего через счетчик, шунтируется через R для защиты гальванометра
- гальванометр : Аналоговый измерительный прибор, обозначаемый буквой G, который измеряет ток, используя отклонение стрелки, вызванное силой магнитного поля, действующей на проводник с током.

- нулевые измерения : методы более точного измерения тока и напряжения путем уравновешивания цепи таким образом, чтобы ток не протекал через измерительное устройство
- потенциометр : прибор, который измеряет напряжение, противопоставляя ему точную долю известного напряжения и не потребляя ток от неизвестного источника.
- Мост Уитстона : Прибор, используемый для измерения неизвестного электрического сопротивления путем уравновешивания двух ветвей мостовой схемы, одна из которых включает неизвестный компонент.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- Колледж OpenStax, Колледж физики.
 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Вольтметры. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Вольтметры . Лицензия : CC BY-SA: Attribution-ShareAlike
- Амперметров. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Амперметры . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.
 com//physics/definition/galvanometer . Лицензия : CC BY-SA: Attribution-ShareAlike
com//physics/definition/galvanometer . Лицензия : CC BY-SA: Attribution-ShareAlike - Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/shunt-resistance . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Вольтметры и амперметры. Расположен по адресу : http://www.youtube.com/watch?v=z6-c4jLXkMo . Лицензия : Общественное достояние: Нет данных Авторские права .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Вольтметры. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Вольтметры . Лицензия : CC BY: Attribution
- Потенциометр (измерительный прибор). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Potentiometer_(measuring_instrument) . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42362/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42362/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution - Мост Уитстона. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Wheatstone_bridge . Лицензия : CC BY-SA: Attribution-ShareAlike
- потенциометр. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/potentiometer . Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.
 boundless.com//physics/definition/null-measurements . Лицензия : CC BY-SA: Attribution-ShareAlike
boundless.com//physics/definition/null-measurements . Лицензия : CC BY-SA: Attribution-ShareAlike - Мост Уитстона. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/Wheatstone_bridge . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Вольтметры и амперметры. Расположен по адресу : http://www.youtube.com/watch?v=z6-c4jLXkMo . Лицензия : Общественное достояние: Нет данных Авторские права .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Вольтметры. Предоставлено : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Вольтметры . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 26 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42362/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.


 6 кОм
6 кОм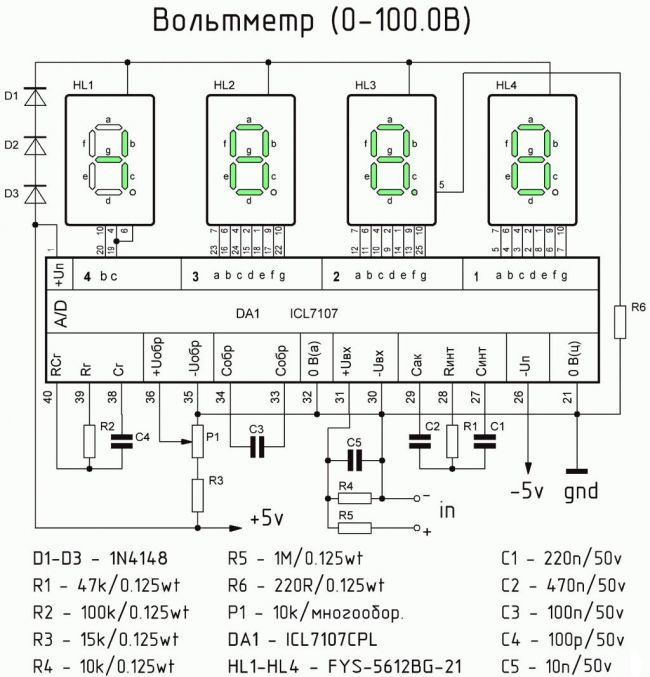

 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42360/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution  com//physics/definition/galvanometer . Лицензия : CC BY-SA: Attribution-ShareAlike
com//physics/definition/galvanometer . Лицензия : CC BY-SA: Attribution-ShareAlike  Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42362/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42362/latest/?collection=col11406/latest . Лицензия : CC BY: Attribution  boundless.com//physics/definition/null-measurements . Лицензия : CC BY-SA: Attribution-ShareAlike
boundless.com//physics/definition/null-measurements . Лицензия : CC BY-SA: Attribution-ShareAlike  Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube