РАСЧЕТ ПАРАМЕТРОВ ЛИСТОГИБОЧНЫХ НЕСИММЕТРИЧНЫХ ТРЕХВАЛКОВЫХ ВАЛЬЦОВ ПРИ ПРОИЗВОДСТВЕ СТАЛЬНЫХ ТРУБ | Шинкин
1. Banabic D. (Ed.). Multiscale modeling in sheet metal forming. – Heidelberg: Springer, 2016. – 405 p.
2. Hingole R.S. Advances in metal forming. Expert system for metal forming. – Heidelberg: Springer, 2015. – 116 p.
3. Davim J.P. (Ed.). Materials Forming and Machining. Research and Development. – Woodhead Publishing, 2015. – 202 p.
4. Lenard J.G. (Ed.). Metal forming science and practice. – Oxford: Elsevier Science, 2002. – 378 p.
5. Hu J., Marciniak Z., Duncan J. Mechanics of sheet metal forming. – Oxford – Boston: Butterworth-Heinemann, 2002. – 211 p.
6. Calladine C.R. (Ed.). Plasticity for engineers. Theory and applications. – Woodhead Publishing, 2000. – 328 p.
7. Belsky S.M., Mazur I.P., Lezhnev S.N., Panin E.A. A two-zone model of browdening during rolling // Journal of Chemical Technology and Metallurgy. 2017. Vol. 52. No. 2.
P. 180 – 185.
8. Belskiy S., Mazur I., Lezhnev S., Panin E. Distribution of linear pressure of thin-sheet rolling across strip width // Journal of Chemical Technology and Metallurgy. 2016. Vol. 51. No. 4. P. 371 – 378.
9. Belskiy S.M., Yankova S., Chuprov V.B. etc. Temperature field of stripes under hot rolling // Journal of Chemical Technology and Metallurgy. 2015. Vol. 50. No. 6. P. 613 – 616.
10. Muhin U., Koinov T., Belskij S., Makarov E. Application of between-stand cooling in the production of hot-rolled strips // Journal of Chemical Technology and Metallurgy. 2014. Vol. 49. No. 1. P. 65 – 70.
11. Muhin U., Belskij S., Koinov T. Study on the influence of the antibending force of working rolls on the widening in hot rolling of thin sheet // Journal of Chemical Technology and Metallurgy. 2014. Vol. 49. No. 1. P. 77 – 81.
12. Muhin U., Koinov T., Belskij S., Makarov E. Simulation of accelera ted strip cooling on the hot rolling mill run-out roller table // Journal of Chemical Technology and Metallurgy.
2014. Vol. 49. No. 1. P. 60 – 64.
13. Belskiy S.M., Mazur S.I., Mukhin Y.A., Goncharov A.I. Influence of the cross section of hot-rolled steel on the flatness of cold-rolled strip // Steel in Translation. 2013. Vol. 43. No. 5. P. 313 – 316.
14. Belskiy S.M., Mukhin Y.A. Classifi cation of regulation principles for strip fl atness // Steel in Translation. 2009. Vol. 39. No. 11. P. 1012 – 1015.
15. Belskiy S.M., Mukhin Y.A. Hot strip rolling with local thickening // Steel in Translation. 2009. Vol. 39. No. 5. P. 420 – 424.
16. Belskiy S.M., Tret’yakov V.A., Baryshev V.V., Kudinov S.V. In vestigation of slab width formation in roughing group of broad strip mill // Steel in Translation. 1998. Vol. 28. No. 1. P. 32 – 39.
17. Коцарь С.Л., Третьяков В.А., Бельский С.М., Полякова Б.А., Савочкин А.Г. Экспериментальная проверка математических моделей прокатки с имитацией осевой сдвижки валков // Сталь. 1993. № 2. С. 53 – 55.
18. Shinkin V.N., Kolikov A.P. Simulation of the shaping of blanks for large-diameter pipe // Steel in Translation.
2011. Vol. 41. No. 1. P. 61 – 66.
19. Shinkin V.N., Kolikov A.P. Elastoplastic shaping of metal in an edge-bending press in the manufacture of large-diameter pipe // Steel in Translation. 2011. Vol. 41. No. 6. P. 528 – 531.
20. Shinkin V.N., Kolikov A.P. Engineering calculations for processes involved in the production of large-diameter pipes by the SMS Meer technology // Metallurgist. 2012. Vol. 55. No. 11-12. P. 833 – 840.
21. Shinkin V.N. The mathematical model of the thick steel sheet flattening on the twelve-roller sheet-straightening machine. Mas sage 1. Cur vature of sheet // CIS Iron and Steel Review. 2016. Vol. 12. P. 37 – 40.
22. Shinkin V.N. The mathematical model of the thick steel sheet flattening on the twelve-roller sheet-straightening machine. Massage 2. Forces and moments // CIS Iron and Steel Review. 2016. Vol. 12. P. 40 – 44.
23. Shinkin V.N. Geometry of steel sheet in a seven-roller straightening machine // Steel in Translation. 2016. Vol.
46. No. 11. P. 776 – 780.
24. Shinkin V.N. Preliminary straightening of thick steel sheet in a seven-roller machine // Steel in Translation. 2016. Vol. 46. No. 12. P. 836 – 840.
25. Il’ichev V.G., Zalavin Ya.E. Improving the roller shaping of largediameter pipe from strip // Steel in Translation. 2016. Vol. 46. No. 1. P. 54 – 57.
26. Yusupov V.S., Kolobov A.V., Akopyan K.E. etc. Improving the production of electrowelded straight-seam pipe. Part 2 // Steel in Translation. 2015. Vol. 45. No. 12. P. 975 – 977.
27. Yusupov V.S., Kolobov A.V., Akopyan K.E. etc. Improving the production of electrowelded straight-seam pipe. Part 1 // Steel in Translation. 2015. Vol. 45. No. 8. P. 598 – 604.
28. Klyukvin M.B., Ordin V.G., Matrosov Yu.I. etc. Change in X80 steel plate mechanical properties during pipe manufacture // Metallurgist. 2012. Vol. 56. No. 7-8. P. 591 – 596.
29. Shabalov I.P., Solov’ev D.M., Filippov G.A., Livanova O.V. Infl uence of UO shaping on the mechanical properties of largediameter electrowelded pipe // Steel in Translation.
2015. Vol. 45. No. 4. P. 287 – 292.
30. Manzhurin I.P., Sidorina E.A. Determination of the reduction in the thickness of strip during its shaping in the rolls of a roll-forming machine. Metallurgist // 2013. Vol. 56. No. 11-12. P. 941 – 945.
31. Punin V.I., Kokhan L.S., Morozov Yu.A. Reduction of the length of strip rolled on roll-forming machines // Metallurgist. 2013. Vol. 56. No. 11-12. P. 938 – 940.
32. Barabash A.V., Gavril’chenko E.Yu., Gribkov E.P., Markov O.E. Straightening of sheet with correction of waviness // Steel in Translation. 2014. Vol. 44. No. 12. P. 916 – 920.
33. Komkov N.A., Livanova O.V., Nikulin A.N., Filippov G.A. Manu facture of plane axisymmetric blanks by end rolling from round bar or thick-walled pipe // Steel in Translation. 2012. Vol. 42. No. 1. P. 73 – 77.
34. Mentyukov K.Yu., Bortsov A.N., Shabalov I.P., Mansyrev E.I. Study of the properties of the base metal of large-diameter pipes under alternating loading // Metallurgist.
2016. Vol. 60. No. 3-4. P. 397 – 404.
35. Shabalov I.P., Nastich S.Yu., Velikodnev V.Ya. etc. Eff ect of heating and deformation on properties of highly deformable pipe metal during cold bend manufacture // Metallurgist. 2017. Vol. 60. No. 9-10. P. 1070 – 1079.
Вальцовка листового металла. Силовой расчет в Excel.
Опубликовано 08 мая 2016
Рубрика: Механика | 22 комментария
В одной из статей блога два с половиной года назад была затронута тема расчета геометрии деталей, получающихся в процессе вальцовки. В этой публикации речь пойдет об определении усилий, возникающих при вальцовке листового металла. Тема интересная…
…и важная не только для специалистов эксплуатирующих листогибочные вальцы, но и для всех, кто, так или иначе, связан с процессом гибки на листогибочных и обычных прессах.
Во всех расчетных формулах для определения усилия гибки листов в качестве одних из главных определяющих параметров фигурируют или предел прочности, или предел текучести металла листовой заготовки.
Известно, что в процессе изгиба область, подверженная деформации, упрочняется. Но на сколько? Иногда это упрочнение учитывают повышающим предел текучести постоянным коэффициентом, как, например, в статье о V-образной гибке. В программе, представленной в этой статье, повышение прочности будет определено и учтено аналитически по расчетной кривой деформационного упрочнения.
В паспортах листогибочных валковых машин в последнее время обычно указывается максимальная ширина и толщина изгибаемой листовой заготовки из стали С255 и наименьший радиус вальцовки. А на практике постоянно возникает вопрос – «потянут» ли вальцы менее широкий, но более толстый лист, да еще, возможно, и из другой марки стали? Вопрос не праздный – ошибка может привести к поломке станка и дорогостоящему последующему ремонту.
Включаем MS Excel и начинаем рассмотрение решения озвученной задачи на примере вальцовки листового металла на трехвалковой листогибочной машине.
Расчет в Excel моментов и сил при вальцовке.
Задача:
Определить возможность гибки и правки обечайки диаметром 1600 мм и длиной 1500 мм из листовой стали С345 (09Г2С) толщиной 18 мм на вальцах марки И2222.
Из паспортных данных машины известно, что на ней можно изготовить обечайку минимальным диаметром 440 мм и длиной 2000 мм из листовой стали С255 (Ст3 сп5) толщиной 16 мм.
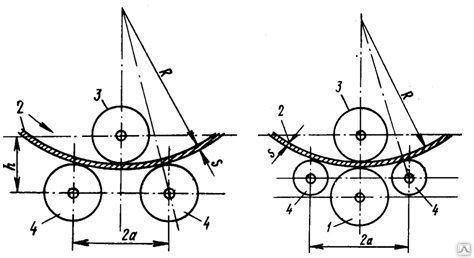
Вальцовка листового металла на трехвалковой машине с подвижным в вертикальной плоскости верхним валком показана на схеме, из которой очевидно, что наиболее нагруженным является верхний валок.
Задачу решим следующим образом:
1. Определим в расчете №1 усилие на верхнем валке при гибке и правке обечайки с предельными размерами из паспорта. То есть узнаем возможности листогибочной машины И2222.
2. В расчете №2 вычислим силы, действующие на наиболее нагруженный верхний валок при гибке и правке интересующей нас короткой трубы из стали С345.
3. Сравним значения сил и сделаем выводы.
Расчет №1:
Расчет №2:
Вывод:
Так как усилия на верхнем валке в расчете №2 немного меньше усилий из расчета в Excel №1, то следует вывод: на вальцах И2222 можно изготовить трубу из стали 09Г2С диаметром 1600 мм, длиной 1500 мм с толщиной стенки 18 мм.
Формулы, использованные в расчете:
12. εт=[σт]/E+0,002
13. m=lg([σв]/[σт])/lg(εв/εт)
14. A=[σв]/(g*εвm)=[σт]/(g*εтm)
15.
n=A*2(2,59-m)/(E/g*(2+m))
16. Rо=R+s/2
17. rо=Rо/s
18. Rг=Rо/(1+n*rо(1-m))
19. Mг=(A*b*s(2+m))/(2(m+1)*(2+m)*Rгm)*g
20. αг=arcsin ((L/2)/(Rг+D/2+s/2))
21. Pг=2*Mг/(Rг*tg (αг))
22.
Rпр=kф*Rг
23. Mпр=(A*b*s(2+m))/(2(m+1)*(2+m)*Rпрm)*g
24. αпр=arcsin ((L/2)/(Rпр+D/2+s/2))
25. Pпр=2*π*Mпр/(Rпр*((π- αпр)*tg (αпр)+1-1/cos (αпр)))
Заключение.
Расчет в Excel был выполнен без учета веса верхнего валка.
Если учесть этот момент, возможности листогибочной машины увеличатся на 2…3%.
Механические свойства сталей в пунктах 4…7 расчета можно найти в ГОСТ 27772-88 (εт=δ5).
При правке заваренных обечаек изгибающий момент и усилие на верхнем валке возрастают из-за неправильной геометрии подогнутых краев заготовки и усиления сопротивления замкнутого контура.
Коэффициент формы обечайки kф в пункте 11 можно определить по подсказке в примечании к ячейке D13.
Этот коэффициент зависит от способа подгибки краев заготовки:
kф=0,75…0,85 – при вальцовке без подкладного листа с плоскими краями;
kф=0,80…0,90 — при вальцовке без подкладного листа по радиусу;
kф=0,85…0,95 — при вальцовке с подкладным листом:
kф=0,95…1,00 – при гибке на прессе в штампе.
В завершении статьи определим коэффициент упрочнения, о котором упоминалось в самом начале, для каждого из рассчитанных выше вариантов.
K1=Mг1/(Wx1*[σт]1)=37783899/(2000*162/6*245)=1,81
K2=Mг2/(Wx2*[σт]2)=42658644/(1500*182/6*325)=1,62
С уменьшением радиуса гибки листа логично нарастает упрочнение. Используя параметры кривой деформационного упрочнения, можно более точно определять усилия и при V-образной гибке на листогибочных прессах.
Ссылка на скачивание файла: raschet-usilij-pri-valcovke (xls 82,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
3-валковый листогибочный станок: анализ нагрузки и расчет приводной мощности (симметричный)
18 февраля 2023 г.
18 февраля 2023 г.
/ 4 минуты чтения
Нагрузка на листогибочный станок значительная, поэтому прочность его деталей должна быть высокой.
Кроме того, в условиях жесткой конкуренции на рынке крайне важно снизить стоимость листовых валков. Это означает, что машина должна быть спроектирована с точностью и надежностью.
Чтобы спроектировать вальцегибочный станок, необходимо сначала выполнить силовой анализ вальцовочного станка, который обеспечивает исходные параметры для проектирования каждой части станка.
Расчет мощности привода системы главного привода также важен для проектирования системы главного привода и выбора двигателя.
Таким образом, расчет силового анализа и приводной мощности листопрокатного станка имеет решающее значение для проектирования вальцегибочного станка.
В этом посте представлен один из методов расчета силовых возможностей симметричного трехвалкового листогибочного станка, и другие типы листопрокатных станков могут использовать его в качестве справочного материала.
Во время работы листопрокатного станка стальной лист должен быть закатан в стальную трубу.
В это время напряжение материала достигло предела текучести.
Следовательно, распределение изгибающего напряжения на сечении трубы показано ниже рисунка (б), а изгибающий момент М сечения равен:
В приведенной выше формуле
- B, δ – Максимальная ширина и толщина листового проката (м)
- σ s – Предел текучести материала (кН • м -2 )
, а коэффициент армирования K вводится для модификации уравнения (1), а именно:
В приведенной выше формуле
- K – коэффициент армирования, значение может быть K = 1,10~1,25, когда результат для δ/R большой, тогда берется наибольшее значение.
- R – Радиус нейтрального слоя прокатываемого листа (м)
2 Силовое состояние При прокатке стального листа силовое состояние показано на рисунке ниже. Согласно балансу сил опорная сила F 2 на пластину валка может быть получена по формуле:
В приведенной выше формуле
- θ – угол между оскверненной линией OO 1 и OO 2,
- α – Нижний ролик. диаметр прокатки листа (м)
- d 2 – Диаметр нижнего ролика (м)
Рис. минимальный диаметр прокатной трубы, радиус R нейтрального слоя около 0,5d мин , для упрощения расчета вышеприведенное уравнение можно изменить на:
В соответствии с балансом сил сила давления F 1 , создаваемая верхним валком, действующая на пластину качения, составляет:
Расчет мощности привода 3.1 Приводной момент нижнего ролика Нижний ролик листопрокатного станка является ведущим роликом, и крутящий момент нижнего ролика используется для преодоления момента деформации T n1 и момент трения T n2 .
В процессе прокатки стального листа деформационная способность, сохраненная в отрезке АВ стального листа (см. рис. 1а и рис. 2), составляет 2 M θ , расчетное время составляет 2 θR/V ( V — скорость прокатки).
Отношение равно мощности момента деформации T n1 , а именно:
Следовательно,
Момент трения включает момент трения качения между верхним и нижним роликом и стальной пластиной, а также момент трения скольжения между шейки ролика и втулки вала, которые можно рассчитать следующим образом:
В приведенной выше формуле:
- F -Коэффициент трения катания, Take F = 0,008M
- μ -коэффициент скользящего трения, Take μ = 0,05-0.1140140140140140140140140140140140140140140140140140140140140140140140 гг.
- d 2 – Диаметр верхнего и нижнего роликов (м)
- D 1 , D 2 – Диаметр шейки верхнего и нижнего роликов (м)
Размер еще не указан в конструкции фаза, значение может принимать D i = 0,5d i (i=1, 2).
Момент T привода нижнего ролика равен сумме момента деформации T n1 и момента трения T n2 .
Приводная мощность нижнего ролика:
В приведенной выше формуле:
- P – Приводная мощность (м • кВт)
- ТН сила – момент силы Н m)
- n 2 – Скорость вращения нижнего ролика (об • мин -1 ), n 2 =2 В /d 2 (V – скорость прокатки)
- η – КПД трансмиссии, η=0,65-0,8
Мощность главного двигателя можно получить от значения P .
2 акции
Анализ нагрузки и расчет приводной мощности симметричного 3-валкового листогибочного станка – Производители листогибочных станков
о 3-валковом листогибочном станке
Поскольку нагрузка на листогибочный станок велика, поэтому требования к деталям прочность высокая.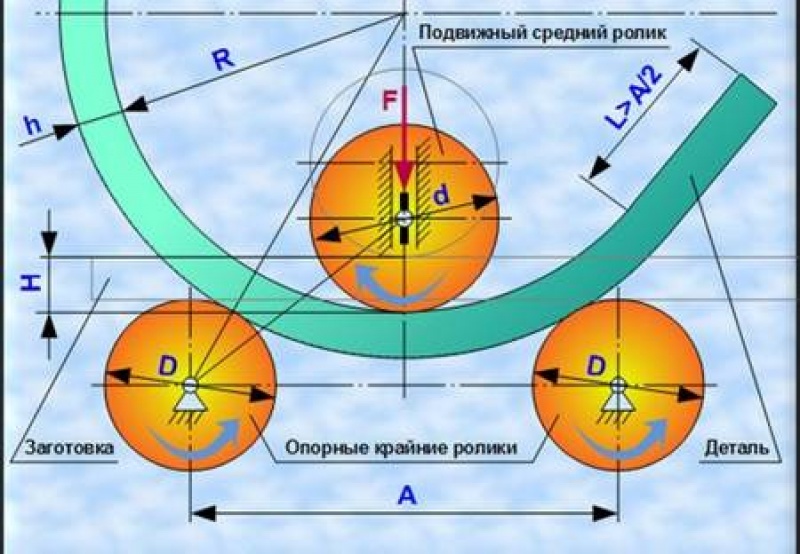
Кроме того, в связи с жесткой конкуренцией на рынке необходимо срочно снизить стоимость листовых валков, поэтому крайне важно спроектировать машину точно и надежно.
Для расчета конструкции вальцегибочного станка сначала требуется силовой анализ вальцовочного станка, результатом которого являются исходные параметры конструкции каждой части листогибочного станка.
Расчет приводной мощности системы главного привода является необходимым параметром для проектирования системы главного привода и выбора двигателя.
Таким образом, расчет силового анализа и приводной мощности листопрокатного станка очень важен для проектирования вальцегибочного станка.
В этом посте расчет силовых возможностей симметричного трехвалкового листогибочного станка является одним из методов, другие типы листопрокатных станков могут использовать его для справки.
Анализ силы
Максимальный крутящий момент, необходимый для прокатки цилиндра
Когда листопрокатный станок работает, стальной лист должен быть закатан в стальную трубу.
В это время напряжение материала достигло предела текучести.
Таким образом, распределение изгибающего напряжения на сечении трубы показано под рисунком (б), а изгибающий момент М сечения равен:
В приведенной выше формуле
стальной лист (м)σs- Предел текучести материала (кН•м-2)
Рис.1 Распределение напряжения при изгибе валка
При рассмотрении деформации материала имеется армирование, и для изменения вводится коэффициент армирования K уравнение (1), а именно:
В приведенной выше формуле
K – коэффициент армирования, значение может быть K = 1,10~1,25, когда результат для δ/R большой, тогда берется наибольшее значение.
R – Радиус нейтрального слоя прокатываемого листа (м)
Силовое состояние
Силовое состояние при прокатке стального листа показано на рисунке ниже. В соответствии с балансом сил поддерживающая сила F2 на листе валка может быть получена по формуле:
В приведенной выше формуле
θ – угол между линиями отклонения OO1 и OO2,
α – Межцентровое расстояние нижнего валка (м)
dmin – Минимальный диаметр прокатки листа (м)
d2 – Диаметр нижнего валка (м)
пластина δ намного меньше минимального диаметра прокатной трубы, радиус R нейтрального слоя составляет около 0,5 dmin, чтобы упростить расчет, приведенное выше уравнение можно изменить на:
Расчет мощности привода
Приводной момент нижнего ролика
Нижний ролик листопрокатного станка является ведущим роликом, и приводной момент на нижнем ролике используется для преодоления момента деформации Tn1 и момента трения Tn2.
