Как из дробной перевести в десятичную: Как перевести обыкновенную дробь в десятичную?

Содержание

Как перевести обыкновенную дробь в десятичную?

Что такое дробь: понятие

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 5/9 или (1,5 – 0,2)/15.

Алгебраические — состоят из переменных. Например, (x + y)/(x – y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.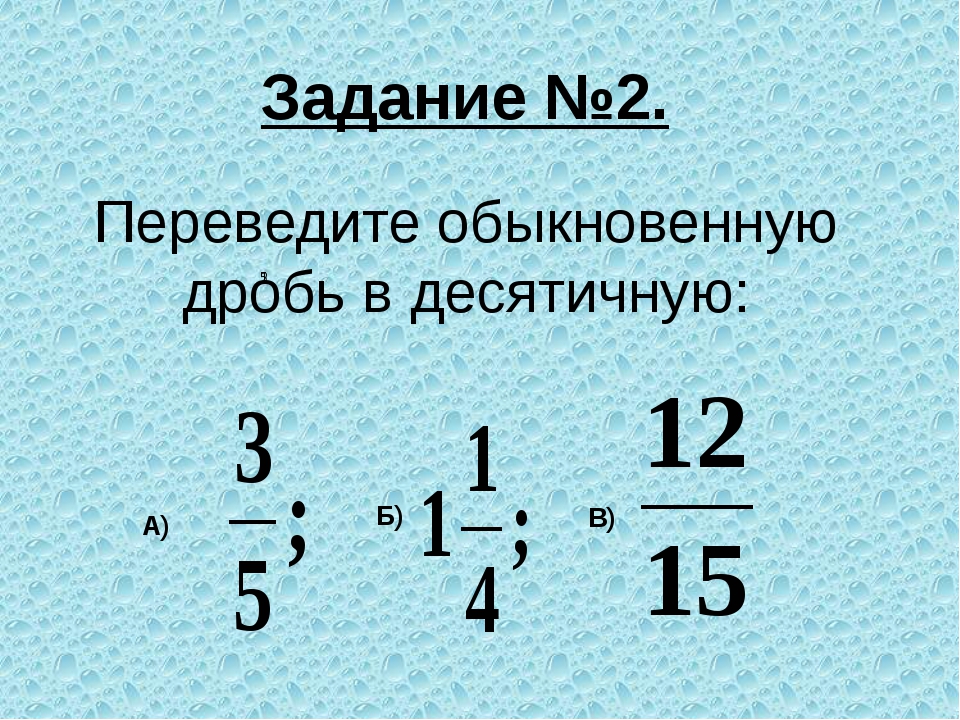

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.

Что такое десятичная дробь

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

0,600 = 0,6
21,10200000 = 21,102

Основные свойства десятичных дробей

Дробь не имеет значения, при условии, если делитель равен нулю.

Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.

Две дроби a/b и c/d называются равными, если a * d = b * c.

Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как перевести обычную дробь в десятичную

Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.

Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:

Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:

Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.

Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.

А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.

Способ 1. Превращаем знаменатель в 10, 100 или 1000

Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.

Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.

Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.

Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.

Еще пример:

Способ 2. Делим числитель на знаменатель

Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.

Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.

Делим столбиком числитель на знаменатель — преобразование готово:

Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333. . = 0,(3).

Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:

Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Еще алгоритм: как преобразовать десятичную дробь в обыкновенную

Посчитать, сколько цифр стоит после запятой. Например, у дроби 0,25 таких цифр две, а у 1,0211 — четыре. Обозначим это количество буквой n.

Переписать исходное число в виде дроби вида a/10ⁿ, где a — это все цифры исходной дроби, а n — количество цифр после запятой, которое мы посчитали в первом шаге. Другими словами, нужно разделить цифры исходной дроби на единицу с n нулями.

Сократить полученную дробь, если это возможно.

Вот и всё! Эта схема значительно проще и быстрее. Проверим:

Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20.

Как перевести периодическую десятичную дробь в обыкновенную

Любую бесконечную периодическую десятичную дробь можно перевести в обыкновенную. Разберем на примерах.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

Вот и ответ!

Если период дроби отличен от нуля — рассматриваем периодическую часть как сумму членов геометрический прогрессии, которая убывает. Поясним на примере:

0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + . .

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен

b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).

Переведем периодическую дробь 0,(7) в обыкновенную.

Запишем: 0,(7) = 0,7 + 0,07 + 0,007 + .. Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1. Применим формулу: 0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 – 0,1) = 0,7/0,9 = 7/9.

Как перевести десятичную дробь в обыкновенную: 3 способа

1 января 2017

Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.

Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная.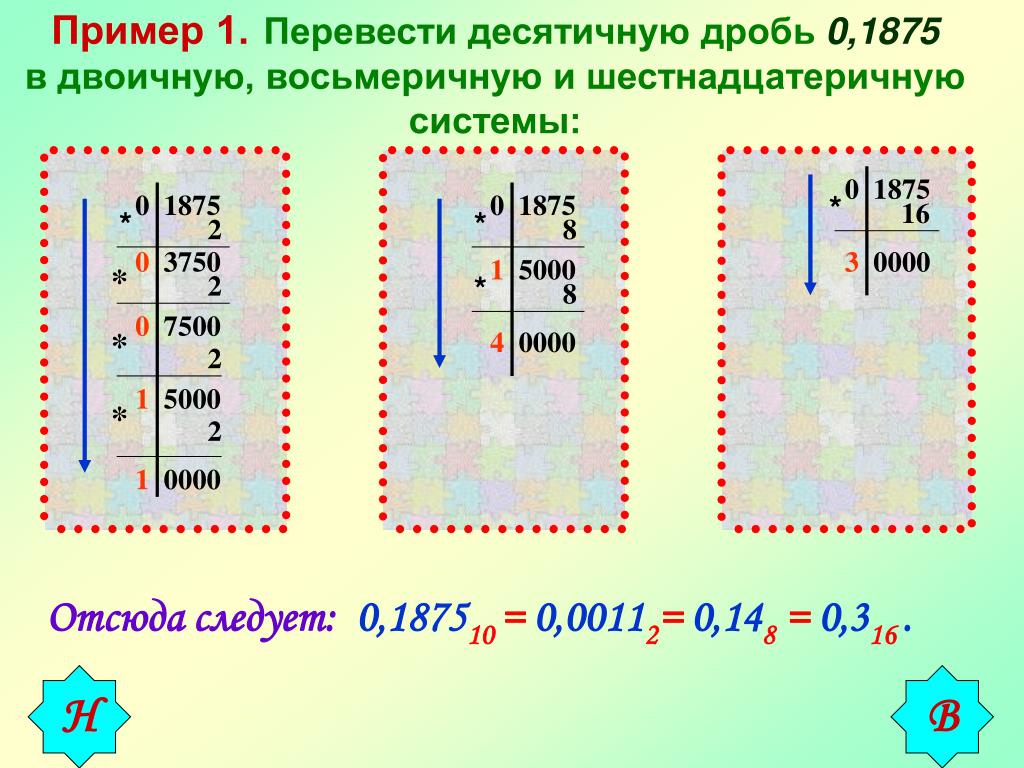

Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:

\[0,75=\frac{3}{4};\quad 1,33=1\frac{33}{100};\quad -7,41=-7\frac{41}{100}\]

Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?

Основной алгоритм

На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.

Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:

Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:
\[0,75=\frac{0,75}{1};\quad 1,33=\frac{1,33}{1};\quad -7,41=\frac{-7,41}{1}\]
Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры: Алгоритм перехода к обычным дробям
Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25. Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)

Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:

Примеры перехода от десятичной записи дробей к обычной

Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.

Наконец, последний пример:

\[1,88=\frac{188}{100}=\frac{47}{25}=\frac{25+22}{25}=1\frac{22}{25}\]

Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.

Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

\[0,88=\frac{88}{100}=\frac{22}{25}\]

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

\[\frac{22}{25}\to 1\frac{22}{25}\]

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Преобразования «на слух»

Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.

А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.

Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:

\[0,004=4:1000=\frac{4}{1000}=\frac{1}{250}\]

Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому

\[2,5=2\frac{5}{10}=2\frac{1}{2}\]

А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому

\[1,125=1\frac{125}{1000}=1\frac{1}{8}\]

В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10³, а 10 = 2 ∙ 5, поэтому

\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]

Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.

На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».

Смотрите также:

Сравнение дробей
Периодические десятичные дроби
Пробный ЕГЭ 2012 от 7 декабря. Вариант 3 (без логарифмов)
Метод Гаусса
Интегрирование по частям
Задача B4: обмен валют в трех различных банках

Как перевести обычную дробь в десятичную

1. Превратите знаменатель в 10, 100 или 1 000

Этот способ очень простой, но он подходит не для каждой дроби.

Для начала умножьте числитель и знаменатель на такое число, которое преобразует нижнюю часть дроби в 10 или 100, 1 000 и так далее.

Допустим, нам нужно перевести дробь с числителем 7 и знаменателем 25. Мы можем получить в нижней части 100: достаточно умножить 25 на 4. Про верхнюю часть тоже не забываем: получаем 28.

Запишите числитель отдельно. Отсчитайте справа в нём столько же знаков, сколько нолей вы получили в знаменателе после умножения, и поставьте запятую. Это и будет искомая десятичная дробь.

В нашем примере в знаменателе 100, значит отсчитываем в числителе два знака и ставим запятую. Получаем 0,28.

Если такой множитель подобрать не удаётся, текущий способ не подходит. Воспользуйтесь следующим.

Сейчас читают 🔥

2. Поделите числитель на знаменатель

Чтобы преобразовать обычную дробь в десятичную, достаточно поделить её верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе.

Если для вас принципиально важно обойтись без вспомогательных устройств, просто поделите числитель на знаменатель столбиком.

Для примера переведём дробь с числителем 7 и знаменателем 25. Поделив 7 на 25 столбиком, получим 0,28.

Важный момент. При делении столбиком вы можете обнаружить, что процесс идёт по кругу и после запятой в результат попадают повторяющиеся цифры. В таком случае эту дробь нельзя перевести в конечную десятичную. Вместо неё у вас получится периодическая дробь. Чтобы записать результат, возьмите повторяющееся число в скобки.

Допустим, нужно перевести дробь с числителем 1 и знаменателем 3. Поделив 1 на 3 столбиком, мы получим бесконечную десятичную дробь 0,333333333… Приведём её к краткому виду 0,(3) — это и будет результат. Читается как «ноль целых и три в периоде».

Читайте также 📕📐✂️

Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры

Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.

Перевод обыкновенных дробей в десятичные

Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.

Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.

Приступим!

Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби

Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.

Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.

Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?

Правило перевода обыкновенных правильных дробей в десятичные

Записываем 0 и ставим после него запятую.
Записываем число из числителя, которое получилось после дописывания нулей.

Теперь перейдем к примерам.

Пример 1. Перевод обыкновенных дробей в десятичные

Переведем обыкновенную дробь 39100 в десятичную.

Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно – количество цифр в числителе совпадает с количеством нулей в знаменателе.

Следуя правилу, записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,39.

Разберем решение еще одного примера по этой теме.

Пример 2. Перевод обыкновенных дробей в десятичные

Запишем дробь 10510000000 в виде десятичной дроби.

Количество нулей в знаменателе равно 7, а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:

000010510000000

Теперь записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,0000105.

Рассмотренные во всех примерах дроби – обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.

Правило перевода обыкновенных неправильных дробей в десятичные

Записываем число, которое находится в числителе.
Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.

Ниже приведем пример на использование этого правила.

Пример 3. Перевод обыкновенных дробей в десятичные

Переведем дробь 56888038009100000 из обыкновенной неправильной в десятичную.

Сначала запишем число из числителя:

56888038009

Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе – пять). Получим:

568880,38009

Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.

Правило перевода смешанных чисел в десятичные дроби

Выполняем подготовку дробной части числа, если это необходимо.
Записываем целую часть исходного числа и ставим после него запятую.
Записываем число из числителя дробной части вместе с дописанными нулями.

Обратимся к примеру.

Пример 4. Перевод смешанных чисел в десятичные дроби

Переведем смешанное число 231710000 в десятичную дробь.

В дробной части имеем выражение 1710000. Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 001710000.

Теперь записываем целую часть числа и ставим после него запятую: 23,..

После запятой записываем число из числителя вместе с нулями. Получаем результат:

231710000=23,0017

Перевод обыкновенных дробей в конечные и бесконечные периодические дроби

Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.

Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.

Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.

Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.

Числитель при делении представляется в виде десятичной дроби – справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.

Пример 5. Перевод обыкновенных дробей в десятичные

Переведем обыкновенную дробь 6214 в десятичный вид.

Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621=621,00

Теперь разделим столбиком 621,00 на 4. Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.

Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.

В итоге мы получаем десятичную дробь 155,25, которая и является результатом обращения обыкновенной дроби 6214

6214=155,25

Рассмотрим решение еще одного примера, чтобы закрепить материал.

Пример 6. Перевод обыкновенных дробей в десятичные

Обратим обыкновенную дробь 21800.

Для этого в столбик разделим дробь 21,000 на 800. Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.

В результате мы получили: 21800=0,02625.

Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.

Пример 7. Перевод обыкновенных дробей в десятичные

Обратим обыкновенную дробь 1944 в десятичную. Для этого выполним деление столбиком.

Мы видим, что при делении повторяются остатки 8 и 36. При этом в частном повторяются цифры 1 и 8. Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.

Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.

1944=0,43(18).

Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие – в бесконечные периодические?

Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.., то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Подытожим сказанное:

Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.

Приведем пример.

Пример 8. Перевод обыкновенных дробей в десятичные

Какая из данных дробей 4720, 712, 2156, 3117 переводится в конечную десятичную дробь, а какая – только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.

Дробь 4720, как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100.

4720=235100. Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.

Разложение знаменателя дроби 712 на множители дает 12=2·2·3. Так как простой множитель 3 отличен от 2 и от 5, данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.

Дробь 2156, во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 38, разложение знаменателя которой на множители дает 8=2·2·2. Следовательно, это конечная десятичная дробь.

В случае с дробью 3117 разложение знаменателя на множители представляет собой само простое число 17. Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.

Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь

Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?

Отвечаем: нет!

Важно!

При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.

Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:

Мы получаем в остатке 0, и на этом деление заканчивается.
Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.

Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.

Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?

Правило перевода десятичных дробей в обыкновенные дроби

В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
При необходимости сокращаем полученную обыкновенную дробь.

Рассмотрим применение данного правила на примерах.

Пример 8. Перевод десятичных дробей в обыкновенные

Представим число 3,025 в виде обыкновенной дроби.

В числитель записываем саму десятичную дробь, отбросив запятую: 3025.
В знаменателе пишем единицу, а после нее три нуля – именно столько цифр содержится в исходной дроби после запятой: 30251000.
Полученную дробь 30251000 можно сократить на 25, в результате чего мы получим: 30251000=12140.

Пример 9. Перевод десятичных дробей в обыкновенные

Переведем дробь 0,0017 из десятичных в обыкновенные.

В числителе запишем дробь 0,0017, отбросив запятую и нули слева. Получится 17.
В знаменатель записываем единицу, а после нее пишем четыре нуля: 1710000. Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?

Сформулируем еще одно правило.

Правило перевода десятичных дробей в смешанные числа.

Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Обратимся к примеру

Пример 10. Перевод десятичной дроби в смешанное число

Представим дробь 155,06005 в виде смешанного числа.

Записываем число 155, как целую часть.
В числителе записываем цифры после запятой, отбросив нуль.
В знаменателе записываем единицу и пять нулей

Поучаем смешанное число: 1556005100000

Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат:

155,06005=155120120000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.

Самый простой случай – период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример 11. Перевод периодической десятичной дроби в обыкновенную

Обратим периодическую дробь 3,75(0).

Отбросив нули справа, получим конечную десятичную дробь 3,75.

Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:

3,75(0)=3,75=375100=154.

Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:

0,(74)=0,74+0,0074+0,000074+0,00000074+..

Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0<q<1, то сумма равна b1-q.

Рассмотрим несколько примеров с применением данной формулы.

Пример 12. Перевод периодической десятичной дроби в обыкновенную

Пусть у нас есть периодическая дробь 0,(8) и нам нужно перевести ее в обыкновенную.

Запишем:

0,(8)=0,8+0,08+0,008+..

Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0,8 и знаменателем 0,1.

Применим формулу:

0,(8)=0,8+0,08+0,008+..=0,81-0,1=0,80,9=89

Это и есть искомая обыкновенная дробь.

Для закрепления материала рассмотрим еще один пример.

Пример 13. Перевод периодической десятичной дроби в обыкновенную

Обратим дробь 0,43(18).

Сначала записываем дробь в виде бесконечной суммы:

0,43(18)=0,43+(0,0018+0,000018+0,00000018..)

Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:

0,0018+0,000018+0,00000018..=0,00181-0,01=0,00180,99=189900.

Полученное прибавляем к конечной дроби 0,43=43100 и получаем результат:

0,43(18)=43100+189900

После сложения данных дробей и сокращения получим окончательный ответ:

0,43(18)=1944

В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.

Перевод десятичных чисел в дробь: онлайн калькулятор

Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:

0,5 = 1/2;
0,25 = 1/4;
1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.

Избавляемся от запятой

Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:

Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

0,5/1 = 5/10;
0,25/1 = 2,5/10 = 25/100;
1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3: Сокращаем полученные дроби до удобоваримого вида:

5/10 = 1 × 5 / 2 × 5 = 1/2;
25/100 = 1 × 25 / 4 × 25 = 1/4;
1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.

Избавляемся от запятой еще проще

Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.

Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.

Шаг 2: Теперь нам достаточно представить дробь в виде C/10ⁿ, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10³ = 1375/1000;
для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10⁶ = 625/1000000.

По сути, 10ⁿ – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.

Шаг 3: Сокращаем нули и получаем итоговый результат:

1375/1000 = 11 × 125 / 8 × 125 = 11/8;
625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.

0,025 = 25/1000 = 1/40

Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни

На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.

Работа

Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.

0,4 = 4/10 = 2/5

Быт

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Заключение

Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.

Перевод чисел в различных системах счисления

Перевод чисел в различных системах счисления.

Для перевода числа из десятичной системы счисления в систему счисления с другим основанием поступают следующим образом:

а) Для перевода целой части числа его делят нацело на основание системы, фиксируя остаток. Если неполное частное не равно нулю продолжают делить его нацело. Если равно нулю остатки записываются в обратном порядке.

б) Для перевода дробной части числа ее умножают на основание системы счисления, фиксируя при этом целые части полученных произведений. Целые части в дальнейшем умножении не участвуют. Умножение производиться до получения 0 в дробной части произведения или до заданной точности вычисления.

в) Ответ записывают в виде сложения переведенной целой и переведенной дробной части числа.

Пример: перевод чисел из десятичной системы счисления в двоичную систему счисления.

Перевести число 75,375 в двоичную систему счисления.

а) переведем в двоичную систему целую часть – 75

75 : 2 = 37 ( 1 )

37 : 2 = 18 ( 1 )

18 : 2 = 9 ( 0 )

9 : 2 = 4 ( 1 )

4 : 2 = 2 ( 0 )

2 : 2 = 1 ( 0 )

1 : 2 = 0 ( 1 )

Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:

75=1001011₂

б) переведем в двоичную систему дробную часть – 0,375

0,375

0,750

1,500

1,000

Выделенные числа запишем в естественном порядке и получим дробное число в двоичной системе счисления:

0,375 = 0,011₂

в) получив целую и дробную части числа в двоичном виде (75=1001011₂и0,375 = 0,011₂) можем сделать вывод:

75,375=75+0,375 = 1001011₂+0,011₂=1001011,011₂, значит 75,375=1001011,011₂

Пример: перевод чисел из десятичной системы счисления в шестнадцатеричную систему счисления.

Представить десятичное число 157,23 в шестнадцатеричной системе счисления. Целая часть числа равна 157, дробная – 0,23.

а) переведем в двоичную систему целую часть – 157

157 : 16 = 9 (13 или D)

9 : 16 = 0 ( 9 )

Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:

157=9D₁₆

а) переведем в двоичную систему дробную часть – 0,23.

Результат умножения 0,23 на 16 равен 3,68. Целая часть этого числа равна 3, значит первый коэффициент дробной части равен 3. Дробная часть равна 0,68. Снова умножим ее на основание системы: 0,68*16=10,88. Целая часть равна 10 или в шестнадцатеричной системе А. Дробная часть равна 0,88, она опять умножается на 16 и так далее.

Выпишем весь процесс:

0,23 * 16 = 3,68 ( 3 )

0,68 * 16 = 10,88 ( А )

0,88 * 16 = 14,08 ( Е )

0,08 * 16 = 1,28 ( 1 )

0,28 * 16 = 4,48 ( 4 )

0,48 * 16 = 7,68 ( 7 )

0,68 * 16 = 10,88 ( А )

0,88 * 16 = 14,08 ( Е )

0,08 * 16 = 1,28 ( 1 )

0,28 * 16 = 4,48 ( 4 )

0,48 * 16 = 7,68 ( 7 )

0,68 * 16 = 10,88 ( А )

0,88 * 16 = 14,08 ( Е )

Замечаем, что последовательность чисел 0,68; 0,88; 0,08; 0,28; 0,48 повторилась уже 2 раза и начинается в третий раз. Получается бесконечная шестнадцатеричная дробь в которой период (бесконечно повторяемая последовательность цифр) заключен в скобки:

157,23=9D,3(АЕ147)₁₆

Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются.

Пример: перевод чисел из двоичной системы счисления в десятичную систему счисления

Перевести число 1001011,011₂ в десятичную систему счисления

1001011,011₂= 1*2⁶+0*2⁵+0*2⁴+1*2³+0*2²+1*2¹+1*2⁰+0*2^-1+1*2^-2+1*2^-3 =64+8+2+1+0,25+0,125=75,375

Двоичная система проста, так как использует две цифры, но громоздка. В десятичной хранить числа в памяти возможно, но сложен перевод из десятичной в двоичную и обратно и занимает много времени. Необходима система счисления компактнее двоичной, но с более простым переводом.

2³= 8 0, 1, 2, 3, 4, 5, 6, 7.

Для перевода из двоичной системы счисления в восьмеричную необходимо разбить данное двоичное число вправо и влево от запятой на триада ( три цифры ) и представить каждую триаду соответствующим восьмеричным кодом. При невозможности разбиения на триады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру восьмеричного числа представляют соответствующей триадой двоичного кода.

Десятичная система счисления	Двоичная система счисления		Восьмеричная система счисления	Шестнадцатеричная система счисления
Десятичная система счисления	Триады (0-7)	Тетрады (0-15)	Восьмеричная система счисления	Шестнадцатеричная система счисления
0	000	0000	00	0
1	001	0001	01	1
2	010	0010	02	2
3	011	0011	03	3
4	100	0100	04	4
5	101	0101	05	5
6	110	0110	06	6
7	111	0111	07	7
8		1000	10	8
9		1001	11	9
10		1010	12	A
11		1011	13	B
12		1100	14	C
13		1101	15	D
14		1110	16	E
15		1111	17	F
16	10000		20	10

Пример: перевод чисел из двоичной системы счисления в восьмеричную систему счисления.

Переведем число 1001011,011₂ в восьмеричную систему счисления. Разобьем данное число на триады, приписав слева недостающие нули:

001 001 011 , 011

1 1 3 , 3

и заменим каждую триаду соответствующим восьмеричным кодом (см. таблицу). Можем сделать вывод:

1001011,011₂ = 113,3₈

Пример: перевод чисел из восьмеричной системы счисления в двоичную систему счисления.

Переведем число 347,25₈ в двоичную систему счисления. Каждую цифру восьмеричного числа заменим соответствующей триадой (см. таблицу).

3 4 7 , 2 5

011 100 111 , 010 101

Запишем ответ, удалив нули слева в записи числа:

347,25₈ = 11100111,010101₂

Восьмеричная система компактнее двоичной и с более простым переводом чисел, однако, современные требования к ЭВМ заставили создавать шестнадцатеричную систему счисления.

2⁴ = 16 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Правило перевода из двоичной системы счисления в шестнадцатеричную: разбить двоичное число вправо и влево от запятой на тетрады ( по 4 цифры ) и представить каждую тетраду соответствующим шестнадцатеричным кодом. При невозможности разбиения на тетрады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру шестнадцатеричного числа представляют тетрадой двоичного кода.

Пример: перевод чисел из двоичной системы счисления в шестнадцатеричную систему счисления.

Переведем число 1001011,011₂ в шестнадцатеричную систему счисления. Разобьем данное число на тетрады, приписав слева в целой части, и справа в дробной части недостающие нули:

0100 1011, 0110

4 В , 6

и заменим каждую тетраду соответствующим шестнадцатеричным кодом (см. таблицу). Можем сделать вывод:

1001011,011₂ = 4В,6₁₆

Пример: перевод чисел из шестнадцатеричной системы счисления в двоичную систему счисления.

Переведем число А4F,C5₁₆ в двоичную систему счисления. Каждую цифру шестнадцатеричного числа заменим соответствующей тетрадой (см. таблицу).

A 4 F , C 5

1010 0100 1111 , 1100 0101

Запишем ответ, удалив нули слева в записи числа:

A4F,C5₁₆ = 101001001111,11000101₂

В МЕНЮ

Используются технологии uCoz

Пояснения десятичную дробь преобразуем.

Перевод обыкновенных дробей в конечные и бесконечные периодические дроби

Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.

1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:

Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:

Примеры:

2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).

При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:

*Подробнее:

15:13 = 1 остаток 2

4:3 = 1 остаток 1

9:5 = 1 остаток 4

А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:

Например:

*Числитель у нас – это делимое, знаменатель – это делитель.

Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):

3. Десятичную переводим в обыкновенную.

Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015

Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:

*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.

4. Обыкновенную переводим в десятичную.

Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:

Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:

Если имеется целая часть, то тоже ничего сложного:

Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:

А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:

На какие числа умножать числитель и знаменатель?

Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:

Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Говоря сухим математическим языком, дробь – это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

0,5 = 1/2;
0,25 = 1/4;
1,375 = 11/8.

Избавляемся от запятой

Шаг 1 : Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2 : После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

0,5/1 = 5/10;
0,25/1 = 2,5/10 = 25/100;
1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3 : Сокращаем полученные дроби до удобоваримого вида:

5/10 = 1 × 5 / 2 × 5 = 1/2;
25/100 = 1 × 25 / 4 × 25 = 1/4;
1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Избавляемся от запятой еще проще

Шаг 1 : Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 – шесть. Это количество мы обозначим буквой n.

Шаг 2 : Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.

По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень – достаточно указать 1 с n нулей.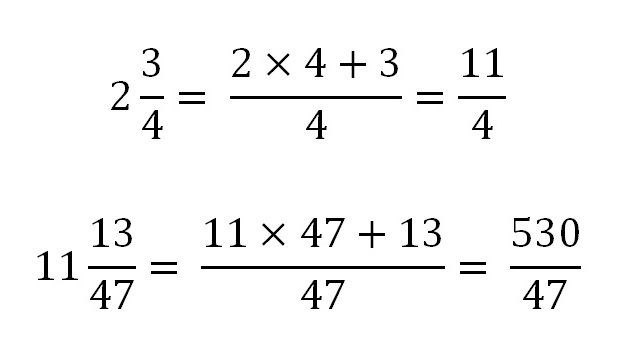 После этого столь богатую на нули дробь желательно сократить.

Шаг 3 : Сокращаем нули и получаем итоговый результат:

1375/1000 = 11 × 125 / 8 × 125 = 11/8;
625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 – это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

0,025 = 25/1000 = 1/40

Примеры использования дробей в повседневной жизни

Работа

0,4 = 4/10 = 2/5

Быт

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % – это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Заключение

Зачастую дети, которые учатся в школе, интересуются, для чего в им в реальной жизни может понадобится математика, в особенности те разделы, которые уже заходят намного дальше, чем простой счет, умножение, деление, суммирование и отнимание. Многие взрослые также задаются данным вопросом, если их профессиональная деятельность очень далека от математики и разнообразных вычислений. Однако стоит понимать, что ситуации бывают всякие, и порой никак не обойтись без той самой, пресловутой школьной программы, от которой мы так пренебрежительно отказывались в детстве. К примеру, вовсе не все знают, как перевести дробь в десятичную дробь, а такие знания могут чрезвычайно пригодится, для удобства счета. Для начала, нужно полностью убедиться, что нужная вам дробь может быть преобразована в конечную десятичную. То же самое касается и процентов, которые также можно легко перевести в десятичные дроби.

Проверка обычной дроби на возможность перевода ее в десятичную

Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.

Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.

Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.

Рассмотрим примеры:

Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.

Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.

Перевести обычную дробь в десятичную возможно несколькими способами

После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.

Как переводить дроби в десятичные: наиболее простой метод

Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.

Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.

Рассмотрим примеры:

Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:

После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.

Можно рассмотреть дополнительный пример, для наглядности:

Второй и боле популярный способ

переводить дроби в десятичные

Второй вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.

Стоит запомнить

Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.

Рассмотрим действие на примере:

Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.

После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».

Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.

Как перевести проценты в десятичную дробь : нет ничего проще

Вот наконец дошел ход и до процентов, которые, оказывается, как гласит все та же, школьная программа, можно перевести в десятичную дробь. Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.

Начать, пожалуй, нужно с определения, то есть разобраться, что такое, собственно, проценты. Процент – это одна сотая часть от какого-либо числа, то есть, абсолютно произвольно. От сотни, к примеру, это будет единица и так далее.

Таким образом, чтобы перевести проценты в десятичную дробь, нужно попросту убрать значок %, а потом разделить само число на сотню.

Рассмотрим примеры:

Причем, чтобы произвести обратную «конвертацию», нужно попросту сделать все наоборот, то есть, число нужно умножить на сотню и приписать к нему значок процента. Точно таким же образом, посредством применения полученных знаний, можно также и обычную дробь перевести в проценты. Для этого достаточно будет просто сперва преобразовать обычную дробь в десятичную, а потому уже ее перевести в проценты, а также легко можно произвести и обратное действие. Как видите, ничего сверхсложного нет, все это элементарные знания, которые просто необходимо держать в уме, в особенности, если имеете дело с цифрами.

Путь наименьшего сопротивления: удобные онлайн сервисы

Бывает и так, что считать совершенно не хочется, да и попросту нет времени. Именно для таких случаев, или же, особо ленивых пользователей, в сети интернет есть множество удобных и простых в применении сервисов, которые позволят перевести обычные дроби, а также проценты, в десятичные дроби. Это действительно дорога наименьшего сопротивления, потому пользоваться подобными ресурсами – одно удовольствие.

Полезный справочный портал «Калькулятор»

Для того, чтобы воспользоваться сервисом «Калькулятора», достаточно просто перейти по ссылке http://www.calc.ru/desyatichnyye-drobi.html , и ввести необходимые числа в нужные поля. Причем ресурс позволяет переводить в десятичные, как обычные, так и смешанные дроби.

После краткосрочного ожидания, приблизительно секунды в три, сервис выдаст конечный результат.

Точно таким же образом можно перевести в обычную дробь десятичную.

Онлайн-калькулятор на «Математическом ресурсе» Calcs.su

Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.

Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.

В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.

Мы уже говорили, что дроби бывают обыкновенные и десятичные . На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.

Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходиться сочетать. То есть, при решении задач приходиться применять оба вида дробей.

Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.

Содержание урока

Выражение величин в дробном виде

Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:

Это выражение означает, что один дециметр был поделен на десять частей, и от этих десяти частей была взята одна часть:

Как видно на рисунке, одна десятая часть дециметра это один сантиметр.

Рассмотрим следующий пример. Показать 6 см и ещё 3 мм в сантиметрах в дробном виде.

Итак, требуется выразить 6 см и 3 мм в сантиметрах, но в дробном виде. 6 целых сантиметров у нас уже есть:

но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. 3 миллиметра это третья часть сантиметра. А третья часть сантиметра записывается как см

Дробь означает, что один сантиметр был разделен на десять равных частей, и от этих десяти частей взяли три части (три из десяти).

В результате имеем шесть целых сантиметров и три десятых сантиметра:

При этом 6 показывает число целых сантиметров, а дробь — число дробных сантиметров. Эта дробь читается как «шесть целых и три десятых сантиметра» .

Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.

Например, запишем без знаменателя. Для этого сначала запишем целую часть. Целая часть это число 6. Записываем сначала это число:

Целая часть записана. Сразу же после написания целой части ставим запятую:

И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:

Любое число, которое представляется в таком виде, называется десятичной дробью .

Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:

6,3 см

Выглядеть это будет следующим образом:

На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части стоят числа 10, 100, 1000 или 10000.

Как и смешанное число, десятичная дробь имеет целую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .

В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.

Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:

Читается как «ноль целых, пять десятых» .

Перевод смешанных чисел в десятичные дроби

Когда мы записываем смешанные числа без знаменателя, мы тем самым переводим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.

После того, как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример:

Сначала

И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать количество нулей в знаменателе дробной части.

Итак, считаем количество нулей в дробной части смешанного числа . В знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2

Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2.

Эта десятичная дробь читается так:

«Три целых, две десятых»

«Десятых» потому что в дробной части смешанного числа находится число 10.

Пример 2. Перевести смешанное число в десятичную дробь.

Записываем целую часть и ставим запятую:

И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.

В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3

Теперь можно перевести это смешанное число в десятичную дробь. Записываем целую часть и ставим запятую:

И записываем числитель дробной части:

Десятичная дробь 5,03 читается так:

«Пять целых, три сотых»

«Сотых» потому что в знаменателе дробной части смешанного числа находится число 100.

Пример 3. Перевести смешанное число в десятичную дробь.

Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.

Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.

В первую очередь смотрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:

Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это число 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед число 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:

Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала целую часть и ставим запятую:

и сразу записываем числитель дробной части

3,002

Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.

Десятичная дробь 3,002 читается так:

«Три целых, две тысячных»

«Тысячных» потому что в знаменателе дробной части смешанного числа находится число 1000.

Перевод обыкновенных дробей в десятичные дроби

Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.

Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.

Пример 1.

Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:

Теперь смотрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой число 5

В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,5 читается так:

«Ноль целых, пять десятых»

Пример 2. Перевести обыкновенную дробь в десятичную дробь.

Целая часть отсутствует. Записываем сначала 0 и ставим запятую:

Теперь смотрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед числом 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:

В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,02 читается так:

«Ноль целых, две сотых».

Пример 3. Перевести обыкновенную дробь в десятичную дробь.

Записываем 0 и ставим запятую:

Теперь считаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед числом 5 дописать четыре нуля:

Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь. Записываем после запятой числитель дроби

В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,00005 читается так:

«Ноль целых, пять стотысячных».

Перевод неправильных дробей в десятичную дробь

Неправильная дробь это дробь, у которой числитель больше знаменателя. Встречаются неправильные дроби, у которых в знаменателе находятся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные дроби. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять целую часть.

Пример 1.

Дробь является неправильной дробью. Чтобы перевести такую дробь в десятичную дробь, нужно в первую очередь выделить у нее целую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к и изучить его.

Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10

Посмотрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Число 11 будет целой частью, число 2 — числителем дробной части, число 10 — знаменателем дробной части.

Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:

Теперь считаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:

В полученной десятичной дроби 11,2 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Значит неправильная дробь при переводе в десятичную дробь обращается в 11,2

Десятичная дробь 11,2 читается так:

«Одиннадцать целых, две десятых».

Пример 2. Перевести неправильную дробь в десятичную дробь.

Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе находится число 100.

В первую очередь выделим целую часть этой дроби. Для этого разделим 450 на 100 уголком:

Соберём новое смешанное число — получим . А как переводить смешанные числа в десятичные дроби мы уже знаем.

Записываем целую часть и ставим запятую:

Теперь считаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:

В полученной десятичной дроби 4,50 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена верно.

Значит неправильная дробь при переводе в десятичную дробь обращается в 4,50

При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5

Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны. Поставим между ними знак равенства:

4,50 = 4,5

Возникает вопрос: а почему так происходит? Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».

Перевод десятичной дроби в смешанное число

Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби. Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:

и рядом три десятых:

Пример 2. Перевести десятичную дробь 3,002 в смешанное число

3,002 это три целых и две тысячных. Записываем сначала три целых

и рядом записываем две тысячных:

Пример 3. Перевести десятичную дробь 4,50 в смешанное число

4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых

и рядом пятьдесят сотых:

Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Попробуем доказать, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.

После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в

Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:

Теперь имеем две дроби и . Настало время вспомнить основное свойство дроби, которое говорит, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не изменяется.

Давайте разделим первую дробь на 10

Получили , а это вторая дробь. Значит и равны между собой и равны одному и тому же значению:

Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.

Перевод десятичной дроби в обыкновенную дробь

Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:

и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .

Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.

0,02 это ноль целых и две сотых. Ноль по не записываем, поэтому сразу записываем две сотых

Пример 3. Перевести 0,00005 в обыкновенную дробь

0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Используются чрезвычайно широко, причем в самых различных сферах человеческой деятельности будь то научные и прикладные вычисления, разработка и эксплуатация различной техники, экономический расчёт и так далее. В виду разного рода причин нередко приходится осуществлять обращение десятичной дроби , равно как и процесс, обратный ей. Следует заметить, что подобные преобразования производятся относительно легко, причем в соответствии с определенными правилами и методиками, существующими в математике уже на протяжении многих сотен лет.

Обращение десятичной дроби в простую

Преобразование десятичной дроби в дробь «обыкновенную » производится достаточно легко и просто. Для этого используется следующая методика: в качестве числителя новой дроби берется число, которое располагается справа от десятичной точки исходного числа, в качестве знаменателя используется число десять, в степени, равной количеству разрядов числителя. Что касается оставшейся целой части, то она сохраняется неизменной. Если же целая часть равна нулю, то после преобразования она просто опускается.

ПРИМЕР 1

Пятьдесят целых двадцать пять сотых равняется пятьдесят целых и двадцать пять разделить на сто равняется пятьдесят целых одна четвертая.

Обращение простой дроби в десятичную

Преобразование простой дроби в десятичную , по сути дела, является обратной обращению десятичной дроби в простую . Её осуществление также не вызывает никаких затруднений и является, по сути дела, довольно простым арифметическим действием. Для того чтобы обратить простую дробь в десятичную нужно разделить числитель на её знаменатель в соответствии с определенными правилами.

ПРИМЕР 1

Необходимо осуществить преобразование обычной дроби пять восьмых в десятичную дробь .

При делении пяти на восемь получается десятичная дробь ноль целых шестьсот двадцать пять тысячных.

Округление результата преобразования простой дроби в десятичную

Следует заметить, что, в отличие от такого процесса, как преобразование десятичной дроби , эта процедура за частую может длиться бесконечно долго. В таких случаях говорят, что результат процедуры обращения обычной дроби в десятичную не может быть точным. Впрочем, практика показывает, что в подавляющем большинстве получение идеально точного результата и не требуется. Как правило, процесс деления заканчивается тогда, когда в его ходе уже получены значения тех десятичных долей, которые представляют в каждом конкретном случае практический интерес.

ПРИМЕР 1

Требуется разрезать кусок масла весом один килограмм на девять одинаковых по своей массе частей. При выполнении этой процедуры оказывается, что масса каждой из них равняется 1 / 9 килограмма. Если по всем правилам осуществлять преобразование этой обычной дроби в дробь десятичную , то получится, что масса каждой из получившихся частей равняется ноль целых и один в периоде килограмма.

Округление ведется по стандартным правилам, предусмотренным в арифметике: если первая из «отбрасываемых» цифр имеет значение 5 и более, то последняя из значимых увеличивается на единицу. В противном случае она остается неизменной.

ПРИМЕР 2

Преобразовать обычную дробь одна восьмых в дробь десятичную.

При делении единицы на восемь получается ноль целых сто двадцать пять тысячных или округлённо – ноль целых тринадцать сотых.

Калькулятор дробей в десятичную

Использование калькулятора

Преобразует дробь в десятичную. Преобразуйте правильные и неправильные дроби в десятичные. Преобразуйте отношение в десятичное. Этот калькулятор показывает шаги и работу по преобразованию дроби в десятичное число.

Как преобразовать дробную часть в десятичную

В дробях черточка дроби означает «разделить на». Итак, чтобы найти десятичный эквивалент дроби, такой как 1/4, вам нужно решить математическую задачу: 1 разделить на 4.
1 ÷ 4 = 0,25

Как превратить дробь в задачу деления

Числа делятся легко с помощью калькулятора. Если вам нужно выполнить длинное деление вручную, поместите верхнее число дроби (числитель) внутри скобки деления, а нижнее число (знаменатель) снаружи, слева от скобки деления.

Дробь ¹/₄ становится 1 ÷ 4.Завершите деление, чтобы преобразовать дробь в десятичную.

Вы можете сначала уменьшить дробь до наименьшего числа, чтобы немного упростить математику с делением в столбик. Например, 9/12 = 9 ÷ 12 = 0,75. Использование длинного деления для решения этой задачи вручную или в уме, уменьшение 9/12 = 3/4, может облегчить задачу. Вы даже можете понять, что 3/4 = 0,75, потому что 3 четверти равны 75 центам.

Сопутствующие калькуляторы

Вы также можете посмотреть наши Калькулятор деления в столбик с десятичными знаками для преобразования дроби в десятичную дробь и просмотра работы, связанной с делением в столбик.

Если вам нужна помощь в сокращении дробей до наименьших значений, см. Упрощающий калькулятор дробей.

Чтобы преобразовать десятичную дробь в дробную, см. Калькулятор десятичных дробей.

Преобразование процентов, десятичных знаков и дробей

Урок 4: Преобразование процентов, десятичных знаков и дробей

/ ru / проценты / проценты в реальной жизни / контент /

Преобразование дробей, десятичных знаков и процентов

Когда мы говорим, мы часто используем разные слова, чтобы выразить одно и то же.Например, мы могли бы описать ту же машину как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные дроби и проценты похожи на слова крошечный , маленький и маленький . Все они просто разные способы выражения частей из целого .

На этом изображении в каждой мерной чашке одинаковое количество сока. Но мы выразили эту сумму тремя способами: дробью, процентом и десятичной дробью.Поскольку они выражают одинаковую величину, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.

Иногда бывает полезно преобразовать один вид чисел в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные дроби и проценты, также поможет вам в изучении более сложной математики.

Дроби и десятичные знаки

Каждую дробь можно записать как десятичную, и наоборот.Возможно, вы не делаете это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, легче вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.

Преобразование дроби в десятичную

Преобразуем дробь в десятичную. Мы будем использовать математический навык, которому вы уже научились: деление в столбик. Чтобы освежить память об этом навыке, вы можете просмотреть наш урок по длинному делению.

Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.

Попробуй!

Преобразуйте каждую из этих дробей в десятичную дробь .

Преобразование десятичной дроби в дробь

Теперь сделаем наоборот. Преобразуем десятичную дробь в дробь.

Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.

Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Если вы складываете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби, чтобы у них был общий знаменатель .

Попробуй!

Преобразуйте эти десятичные дроби в дроби. Обязательно уменьшите до каждой дроби до самой простой формы!

Проценты и десятичные знаки

Знание того, как переводить проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Процентное соотношение в реальной жизни».

Преобразование процента в десятичное число

Преобразовать проценты в десятичные числа на удивление легко. Это займет всего несколько простых шагов.

Щелкните слайд-шоу, чтобы узнать, как преобразовать процент в десятичное число.

Почему это работает?

Преобразовать проценты в десятичные числа настолько просто, что может показаться, что вы что-то упустили. Но не волнуйтесь – это действительно так просто! Вот почему метод, который мы вам показали, работает.

Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты из 100, мы просто ставим проценты выше 100, например:

78% = 78/100

На втором этапе мы преобразуем 78/100 в десятичное число.Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , например:

78 ÷ 100 = 0,78

Так почему мы не показали вам эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них. Вы знаете, что все проценты из 100, так что вы можете не превращать проценты в дроби. Вам нужно разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите десятичную точку на два пробела влево! Таким образом, вы можете получить тот же ответ, выполнив всего один простой шаг.

Попробуй!

Переведите эти проценты в десятичные дроби.

Преобразование десятичной дроби в проценты

А теперь обратим назад то, что вы только что узнали. Преобразуем десятичную дробь в проценты.

Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.

Попробуй!

Вычислите эти десятичные дроби в процентах.

Проценты и дроби

Умение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни.Например, предположим, что вы получили оценку 80% за тест. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов было правильным. Когда ваш учитель ставит оценку за тест, она может сделать наоборот. Если ученик правильно ответил на 8 вопросов из 10, учитель может преобразовать 8/10 в процент, чтобы поставить ученику оценку.

Преобразование процента в дробь

Когда вы переводите процент в дробь, полезно помнить, что проценты всегда из 100. Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».

Щелкните слайд-шоу, чтобы узнать, как преобразовать процент в дробь.

Попробуй!

Запишите эти проценты в виде дробей. Убедитесь, что уменьшил каждую дробь до самой простой формы.

Преобразование дроби в проценты

Для преобразования дроби используются два навыка, которые вы только что освоили: запись дроби в виде десятичной дроби и запись десятичной дроби в виде процента . Давайте посмотрим, как мы можем использовать эти навыки, чтобы преобразовать дробь в процент.

Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.

Попробуй!

Переведите эти дроби в проценты.

Советы и хитрости – Подготовка к тесту Каплана

Один из быстрых способов преобразовать дробь в десятичную дробь на GRE – использовать базовое деление. Например, при делении в столбик дробь 3/4 (то есть 4 превращается в 3, а не наоборот) даст 0,75. К счастью, есть более простые и быстрые способы преобразования дробей в десятичные.Самый важный метод – это, конечно, запоминание обычных преобразований.

Дробь	Десятичная	Процент
1/100	.01	1%
1/50
1/25	.04	4%
1/20	.05	5%
1/10	.1	10%
1/9	.1111111…	11,11%
1/8	.125	12,5%
1/6	16,67%
1/5	,2	20%
1/4	,25	25%
1/3
2/5	.4	40%
1/2	.5	50%
3/5	.6	60%
2/3	.6666666….	66,67%
3/4	0,75	75%
4/5	,8	80%

Вы должны запомнить десятичные преобразования таких обычных дробей. Обратите внимание на третий столбец: если вы хотите преобразовать десятичные дроби в проценты, просто переместите десятичную дробь на два разряда вправо.
Другой метод преобразования дробей в десятичные – это манипулирование дробью так, чтобы знаменатель был равен 10 или 100 (или любой степени 10). Ведь проценты – доли 100.
Вот несколько простых примеров:

Пример 1

Преобразуйте ½ в десятичную дробь, установив знаменатель в степень 10.

Преобразование

Преобразуйте дробь 1/2 в 5/10, просто умножив на 5.Теперь ясно, что 1/2 = 0,5

Пример 2

Преобразуйте 13/20 в десятичную дробь, установив знаменатель в степень 10.

Преобразование

Помните, цель состоит в том, чтобы преобразовать знаменатель в степень 10. Умножьте 20 на 5, чтобы получить 100, и преобразуйте дробь в (5 * 13) / 100, или 65/100. В итоге 13/20 =.65

Пример 3

Преобразуйте 18/30 в десятичную дробь, установив знаменатель в степень 10.

Преобразование

Та же идея с 18/30. В этом случае разделите знаменатель 30 на 3, чтобы получить 10. Затем разделите числитель на 3 (18/3 = 6) и преобразуйте дробь в 6/10 или ,6

Пример 4

Преобразуйте 9/15 в десятичную дробь, установив знаменатель в степень 10.

Преобразование

Как насчет чего-нибудь более жесткого, например, 15 сентября? Тот факт, что вы не можете перейти от 15 к 100 в некотором умножении, не означает, что эта стратегия не сработает. Я могу сначала уменьшить 15 до 5, а затем умножить 5 на 2. Для вычисления разделите числитель на 3, а затем умножьте на 2.
Итак, 9/15 = 3/5 = 6/10 = .6

Пример 5

Преобразуйте 11/40 в десятичное, преобразовав знаменатель в степень 10.

Преобразование

Как насчет 11/40? Просто разделите на 2 и умножьте на 5.
11/40 = 5,5 / 20 = 27,5 / 100 = 0,275

В конце концов, дроби – это всего лишь условное обозначение деления. Пока расчеты просты – в данном случае 11/2 = 5,5, 5,5 * 5 = 27,5 – стратегия выгодна.
Обратите внимание, что эта стратегия не будет работать все время.Однако вряд ли GRE представит вам сложные вычисления; как правило, он будет использовать числа, с которыми легче работать.
Не стесняйтесь практиковать это в своей голове – вот в чем идея. Вы не хотите тратить время на настройку этих расчетов на бумаге. Вы хотите сэкономить время и освободить место на бумаге для заметок.

Дробь в десятичную – преобразование, диаграмма, методы, примеры

Дробь в десятичную дробь – это тип преобразования, который можно определить как процесс преобразования числа, представленного в форме p / q, где p и q принадлежат целым числам, а q не равно 0, в десятичную форму посредством либо преобразованием знаменателя в степень 10, либо методом деления в столбик.Давайте посмотрим, каковы различные способы более точного преобразования дробей в десятичные в этой статье.

Преобразование дробей в десятичные

Любое число, представленное в виде дроби, делится на две части: числитель и знаменатель. Обычно, чтобы преобразовать число из дроби в десятичную форму, мы делим числитель на знаменатель. Дроби представлены в виде q / p, где p 0. В то время как десятичные числа образуются путем соединения целой части числа и дробной части через десятичную точку, например, 7.575. Давайте рассмотрим еще несколько иллюстраций, чтобы подробно понять преобразование дроби в десятичную.

Пример преобразования дробной части в десятичную

Вот пример из реальной жизни, чтобы понять преобразование дроби в десятичную. Эмма делит картон на 12 равных частей. Она нарисовала цветы разных цветов на каждой части картона. Из 12 слотов она зарезервировала 5 равных частей для цветов красного цвета, 3 части для цветов зеленого цвета и 4 части для цветов оранжевого цвета.Запишем долю цветов каждого цвета как в дробной, так и в десятичной форме.

Цветки красного цвета нарисованы в части картона 5/12 или 0,4166.
Цветки зеленого цвета нарисованы на 3/12 или 0,25 части картона.
Цветки оранжевого цвета также нарисованы в 4/12 или 0,333 части картона.

Давайте посмотрим на дробное и десятичное представление, приведенное в таблице ниже, чтобы получить больше ясности о преобразовании дроби в десятичное.

Как преобразовать дробь в десятичную?

Для преобразования дроби в десятичную форму двумя следующими способами.

Метод длинного деления
Преобразуя знаменатель дроби в число, кратное 10.

Преобразование дробей в десятичные с помощью метода длинного деления

Когда число представлено в форме дроби, то есть p / q, мы используем метод деления в столбик, чтобы преобразовать его в десятичную форму.В таком случае мы делим значение числителя на значение знаменателя. Давайте разберемся с этапами преобразования дробной части в десятичную с помощью длинного деления на примере.

Преобразование дробей 4/19 в десятичные.

Шаг 1: В данной дроби 4/19 возьмите цифру 4 в числителе в качестве делимого, а цифру в знаменателе 19 в качестве делителя. В этом случае знаменатель> числитель.
Шаг 2: Мы должны сделать цифру делимого (4) больше, чем цифру числителя (19), поместив 0 рядом с 4 и частным соответственно.Теперь у нас 40 новых дивидендов. (40> 19).
Шаг 3: В частной части важно вставить десятичную дробь (.) После 0 и начать деление.
Шаг 4: Умножьте 19 на число так, чтобы произведение было меньше 40. 19 умножить на 2 будет 38. Цифра, которая появилась в частном, – 2, остаток слева – 2. После введения десятичной дроби в частное мы можем ввести один 0 на каждом шаге деления.
Шаг 5: Теперь новый дивиденд равен 20. Умножьте 19 на число, чтобы произведение было меньше 20.19 умножить на 1 равно 19. Здесь частное равно 1, а полное частное равно (0,21), оставшийся остаток равен 1.
Шаг 6: Повторяйте шаги до тех пор, пока мы не получим 0 в качестве остатка или не менее трех десятичных знаков в частном. Попробуйте прочитать шаги с изображением, приведенным ниже, чтобы лучше понять преобразование дробей в десятичные.

В следующем разделе давайте обсудим другой метод преобразования дроби в десятичную, который заключается в преобразовании знаменателя в число, кратное 10.

Путем преобразования знаменателя

Другой метод преобразования дроби в десятичную дробь – преобразование знаменателя дроби в степени или кратные 10, например 10, 100, 1000 и т. Д. Ниже приведены шаги, показывающие процедуру, включенную в преобразование дробей в десятичные дроби путем преобразования метод знаменателя. Давайте рассмотрим здесь иллюстрацию, чтобы понять это с практической точки зрения.

Пример: Преобразование 7/8 в десятичные.

Шаг 1: Во-первых, мы должны придумать число, на которое мы можем легко умножить знаменатель и числитель на такое число, чтобы мы могли получить кратное или степень 10.
Шаг 2: знаменатель равен 8. (8 умножить на 125 равно 1000).
Шаг 3: Теперь умножьте числитель на то же число, то есть 7 умножьте на 125
. Шаг 4: Умножив цифру числителя дроби на 125, мы получим (7 × 125) = 875
. Шаг 5: После завершения процесса умножения у нас есть знаменатель в единицах мощности или кратных 10.
Шаг 6: Окончательный результат в десятичных дробях: 875/1000 = 0,875.
Обратите внимание, что десятичный разряд в окончательном ответе зависит от количества завершающих нулей, присутствующих в цифре знаменателя.

Дробь в десятичную диаграмму

Дробь в десятичную диаграмму – это прямой способ легко получить преобразованные значения. Диаграмма дает нам значения некоторых наиболее часто используемых дробей в десятичных дробях и наоборот. Дроби могут быть меньше или больше 1. У дробей меньше 1 числитель <знаменатель. Их называют правильными дробями. Дроби, у которых числитель> знаменатель, называются неправильными дробями. Давайте проясним, как будут выглядеть числа при преобразовании дробей в десятичную форму.Ознакомьтесь с нашей конкретной страницей, посвященной дробям в десятичной диаграмме, для правильного понимания.

Калькулятор дробей в десятичную

Проверьте наш калькулятор дробей в десятичные и попробуйте несколько преобразований на вашей стороне. Это бесплатный онлайн-инструмент, который вычисляет десятичную форму заданной дроби. Наш калькулятор поможет вам рассчитать десятичное значение дробей за несколько секунд.

☛ Статьи по теме

Ниже приведен список тем, которые тесно связаны с дробью десятичной дроби.Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath

Часто задаваемые вопросы о дроби до десятичной

Что такое преобразование дроби в десятичную в математике?

Дробь в десятичное в математике называется процедурой, которую мы обычно использовали для преобразования дробного значения в десятичное. При переводе дроби в десятичную дробь делится на части, т.е. числитель делится на знаменатель. Десятичное число дает более точное значение по сравнению с дробями.

Чтобы прочитать обратное преобразование, проверьте преобразование десятичного числа в дробное.

Как отображается преобразование дробей в десятичные?

Дроби записываются в виде p / q, где q ≠ 0, а в десятичных дробях дробная часть и целая часть числа соединяются через десятичную точку, например 0,5.

Как преобразовать дробь в десятичную?

Чтобы преобразовать дробь в десятичную, нам нужно выполнить шаги, указанные ниже.

Числитель дроби будет рассматриваться как делимое, а знаменатель – как делитель.
Если числитель <знаменатель, добавьте десятичную дробь (точку) и 0 после делимого.
Выполните деление.
Если остаток продолжает повторяться, то десятичная дробь может быть остановлена после определенного количества десятичных знаков.
Например, преобразование 4/5 в десятичное дает 0,8.

Каков результат преобразования дроби 22/7 в десятичные числа?

22/7 – иррациональное число с 22 в числителе и 7 в знаменателе.Преобразовав 22/7 в десятичные дроби, мы получим 3,14 с точностью до двух знаков после запятой. Это непрерывное, неповторяющееся десятичное число, продолжающееся до бесконечности.

Как преобразовать 2/3 в десятичную систему с помощью дроби в десятичную диаграмму?

Используя дробь в десятичной диаграмме, значение 2/3 равно 0,666. Чтобы найти десятичное значение 2/3, мы выполняем операцию деления, пока остаток не будет равен 0 или до 3-4 знаков после запятой.

Какой метод используется для преобразования дробной части в десятичную?

Очень простой и удобный метод преобразования дроби в десятичную дробь – деление числителя на знаменатель преобразует дробь в десятичную.

Как преобразовать смешанную дробь в десятичную?

Чтобы преобразовать смешанную дробь в десятичную, нам сначала нужно преобразовать ее в неправильную дробь. Затем разделите числитель на знаменатель, чтобы преобразовать его в десятичное значение.

☛ Прочтите следующие статьи, чтобы получить основы:

Преобразование дробей в проценты

Помните, что процент – это просто особый способ выражения дроби как числа из 100 .

Чтобы преобразовать дробь в проценты, сначала разделите числитель на знаменатель.Затем умножьте десятичную дробь на 100 .

То есть дробь 4 8 может быть преобразован в десятичный разделив 4 к 8 . Его можно преобразовать в проценты, умножив десятичную дробь на 100 .

4 ÷ 8 знак равно 0,5 0,5 × 100 знак равно 50

Итак, дробь 4 8 эквивалентно 50 % .

Пример 1:

Напишите 2 25 в процентах.

С 25 больше чем 2 , чтобы разделить, мы должны добавить десятичную точку и несколько нулей после 2 . Мы можем не знать, сколько нулей добавить, но это не имеет значения. Если мы добавим слишком много, мы можем стереть лишнее; если мы не добавим достаточно, мы можем добавить еще.

Так,

2 25 знак равно 0.08 0,08 × 100 знак равно 8

Следовательно, дробь 2 25 эквивалентно 8 % .

Посмотрите на изображение ниже, оно показывает, что дробь 2 25 такой же как 8 снаружи 100 , то есть, 8 % .

Пример 2:

Напишите 7 4 в процентах.

Делить 7 к 4 .

Так,

7 4 знак равно 1,75 1,75 × 100 знак равно 175

Следовательно, дробь 7 4 эквивалентно 175 % .

Пример 3:

Напишите 1 8 в процентах.

Делить 1 к .

Так,

1 8 знак равно 0,125 0,125 × 100 знак равно 12,5

Следовательно, дробь 1 8 эквивалентно 12,5 % .

Преобразование дробей в десятичные – математика для сделок: объем 1

Мы только что научились переводить дроби в десятичные, а теперь пришло время сделать наоборот.Как вы думаете, как это делается? Если вы догадались, что это обратное тому, что мы только что сделали, то вы правы. Мы начнем с примера, относящегося к десятичным дробям, а затем перейдем к замене футов, дюймов и долей дюйма на футы и десятичные дроби фута.

Мы хотим пойти с:

[латекс] \ LARGE \ dfrac {1} {2} \ text {to} 0,5 [/ латекс]

Еще раз, быстрый и простой способ сделать это – просмотреть несколько примеров. Начните с простой старой дроби и работайте над ее преобразованием в десятичную дробь.

[латекс] \ LARGE \ dfrac {3} {8} [/ латекс]

Это можно сделать несколькими способами, самый простой из которых:

[латекс] \ LARGE3 ÷ 8 = 0,375 [/ латекс]

Вы можете вставить числа в свой калькулятор или использовать длинное деление, чтобы найти ответ.

Вот и все. Готово!

Хорошо, это было довольно просто, но теперь давайте перейдем к более сложному примеру. Мы собираемся заменить число, записанное в футах, дюймах и долях дюйма, на десятичное.

Преобразуйте это число в десятичное:

Шаг 1 : Определите любую часть числа, которая уже находится в работающей форме. В этом случае 7 футов вполне подойдут, и с ними ничего не нужно делать.

Шаг 2 : Возьмите долю дюйма и превратите ее в десятичную дробь.

[латекс] \ LARGE \ dfrac {5} {16} \ text {OR} 5 ÷ 16 = 0,3125 [/ латекс]

Задержитесь здесь на мгновение и спросите себя, в каких единицах измерения 0,3125. Все, что мы сделали, это заменили доли дюйма на десятичные.Теперь мы превратили 9 дюймов и доли дюйма в 9 дюймов с десятичными знаками дюйма.

[латекс] \ LARGE9 \ dfrac {5} {16} \ text {дюймы в} 9,3125 \ text {дюймы} [/ латекс]

Шаг 3 : Измените дюймы и десятичные дроби в дюймах на десятичные числа в футах, используя тот факт, что 1 фут = 12 дюймов.

В последнем разделе, когда мы перешли от десятичных дробей к дробям, мы умножили их на 12, чтобы получить дюймы. Поскольку здесь мы выполняем обратный расчет, переходя от дробей к десятичным, мы в конечном итоге делим на 12 дюймов, чтобы получить десятичные дроби в футе.

[латекс] \ LARGE9.3125 ÷ 12 = 0,776 [/ латекс]

Еще раз спросите себя, какие юниты вы получите здесь. Когда мы берем дюймы и делим их на 12, мы получаем футы или, в данном случае, десятичные дроби фута. Итак, наш окончательный ответ:

Мы рассмотрим еще один пример, а затем позволим вам попробовать пару самостоятельно.

Измените следующее число, записанное в футах, дюймах и долях дюйма, на футы и десятичные дроби фута.

Шаг 1 : Определите любую часть числа, которая уже находится в работающей форме.В этом случае 3 фута годятся, и с ними ничего не нужно делать.

Шаг 2 : Возьмите долю дюйма и превратите ее в десятичную дробь.

[латекс] \ LARGE \ dfrac {3} {8} \ text {OR} 3 ÷ 8 = 0,375 [/ латекс]

Соедините дюймы и десятичные дроби дюйма.

[латекс] \ LARGE6 \ dfrac {3} {8} \ text {дюймы в} 6,375 \ text {дюймы} [/ латекс]

[латекс] \ LARGE6.375 ÷ 12 = 0,531 [/ латекс]

Итак, наш окончательный ответ:

Измените следующие футы, дюймы и доли дюйма на футы и десятичные дроби фута. Просмотрите видеоответы, чтобы убедиться, что вы на правильном пути.

Как преобразовать футы / дюймы / дроби в десятичный формат

Много чисел, с которыми нужно иметь дело, и нет, не очень полезно для выбора номеров лотереи. Но если вы понимаете основные концепции, преобразование этих чисел избавляет вас от риска, и вы обязательно станете победителем.

дюйм	Десятичное значение ножки
1 дюйм	0,0833
2 дюйма	0,167
3 дюйма	0,25	9018	5 дюймов	0,417
6 дюймов	0,5
7 дюймов	0,583
8 дюймов	0.667
9 дюймов	0,75
10 дюймов	0,833
11 дюймов	0,917
12 дюймов	1

0,5 9018

Дробь	Десятичное значение дюйма
1/16	0,0625
1/8	0,125
3/16	0,1875	0,1375	0.25
5/16	0,3125
3/8	0,375
7/16	0,4375
1/2	0,5	0,5
5/8	0,625
11/16	0,6875
3/4	0,75
13/16	0,8125		875
15/16	0,9375

Пример

Преобразование 7′- 4 3/4 дюйма в десятичное значение.

Если вы похожи на меня, я бы сказал, что 7 ‘пока остается 7’.
Смотрю на графики 4 “= 0,333 3/4” = 0,75
0,333 + 0,75 = 1,083 “+ 7” = 8,083
, и я бы записал все это как 8.083 в десятичном формате.

Конечно, вы не можете прибавить десятичное значение фута к десятичному значению дюйма, не преобразовав десятичное значение в дюймах дроби в десятичное значение в футах.

Попробуем еще раз:

Преобразование 7′- 4 3/4 дюйма в десятичное значение.

7 футов пока остается 7.
4 “= 0,333 (преобразование в десятичное число футов: 4 ÷ 12)
3/4 “= 0,75 (преобразовать дробь в десятичную, разделив числитель на знаменатель 3 ÷ 4)
0,75 = 0,0625 (преобразование в десятичное значение фут путем деления 0,75 на 12)
0,333 + 0,0625 = 0,3955 + 7 ‘= 7,3955

Запишите в десятичном виде 7 футов 4 3/4 дюйма = 7,3955. 1/4 9018

	1/16	0.0625	0,005208
	1/8	0,125	0,01042
	3/16	0,1875	0,015625	0,1875	0,015625
						5/16	0,3125	0,026004
	3/8	0,375	0,03125
	7/16	0.4375	0,036458
	1/2	0,5	0,041666
	9,16	0,5625	0,046875
	0,046875
										9018 / 16	0,6875	0,057291
	3/4	0,75	0,0625
	13/16	0.8125	0,0677
	7/8	0,875	0,072916
	15/16	0,9375	0,078125						9018
2 дюйма	24/12	2	0,167
3 дюйма	36/12	3	0,25
4 дюйма				48/18 .333
5 дюймов	60/12	5	0,417
6 дюймов	72/12	6	0,5
7 дюймов	7 дюймов		7 дюймов		0,583
8 дюймов	96/12	8	0,667
9 дюймов	108/12	9	0,75
10 дюймов	0.833
11 дюймов	132/12	11	0,917
12 дюймов	144/12	12	1

006 Преобразование дюймов в десятичные

Разделите количество дюймов на 12

Пример:

 2 "÷ 12 = 0,16667
5 "÷ 12 = 0,41667

Преобразование дюймов плюс дробь в десятичную

Превратите дюйм в дробь, используя тот же знаменатель, что и дробь, прибавьте дробь к этой величине и разделите числитель на знаменатель.
2 1/4 дюйма
8/4 + 1/4 = 9/4 дюйма
9/4 = 2,25 дюйма

3 11/16 дюйма
48/16 + 11/16 = 59/16 дюйма
59/16 = 3,6875 дюйма

Воспользуйтесь нашим калькулятором для преобразования футов / дюймов / дробей в десятичный формат